高桩码头桩基局部偏位的平面简化计算法

李志云，池海，张晋恺

（中交第一航务工程勘察设计院有限公司，天津 300222）

0 引言

高桩码头为透空式水工建筑物，采用桩基基础，作为应用广泛的主要码头结构形式对建设地质条件的适应能力最强，能适应各种深水化、大型化港口的建设，建设生态环境的影响最小，在国内外工程建设过程中被越来越多地采用。桩基础作为高桩码头安全的根基，直接影响着码头的耐久性和安全性[1]。然而桩基打设过程中不仅受到波浪、水流、风和施工定位等影响，而且受地形、地质的影响较大，故打桩偏位超出规范容许值的现象在施工中较为常见[2]。

目前针对桩基偏位对结构内力的影响多是通过有限元软件进行数值计算的[3]，方法较为繁琐，本文拟结合黄骅四期码头工程，采用一套简化的设计方法进行分析桩基偏位对自身和码头承载力的局部影响。

1 工程简介

黄骅四期码头工程为1个5万吨级煤炭装船泊位，码头平台采用高桩梁板结构，桩型采用650 mm×650 mm预应力钢筋混凝土空心方桩，排架间距7.0 m。每个排架下设置8根桩，基桩持力层选为粉质黏土层，桩长约50 m。其中前轨下设置3根桩，2根直桩和1根斜桩，斜桩斜度4∶1；后轨和排污管沟梁下分别对称布置1对斜桩，桩的斜度分别为6∶1和4∶1；后边梁下设置1根直桩。上部结构纵横梁均采用预应力钢筋混凝土结构，预制轨道梁宽1 000 mm，高1 800 mm；预制排污管沟梁宽1 400 mm，高1 400 mm；预制横梁宽1 200 mm，高2 000 mm。面板采用预应力空心板，板厚为550 mm，码头面设置现浇混凝土磨耗层。

根据国内现有施工能力，桩基偏位大多都能控制在规范要求之内[4-5]，很少出现打桩偏位500 mm以上。为了让计算方法能更好地解决实际问题，反映桩基偏位对码头结构承载力的影响，选取典型的斜桩进行横向偏位500 mm。则此时叉桩的合力作用点横向偏位值为250 mm。

桩基偏位平面布置图见图1，桩基偏位断面图见图2。

图1 桩基偏位平面布置图Fig.1 Layout of pile foundation deviation

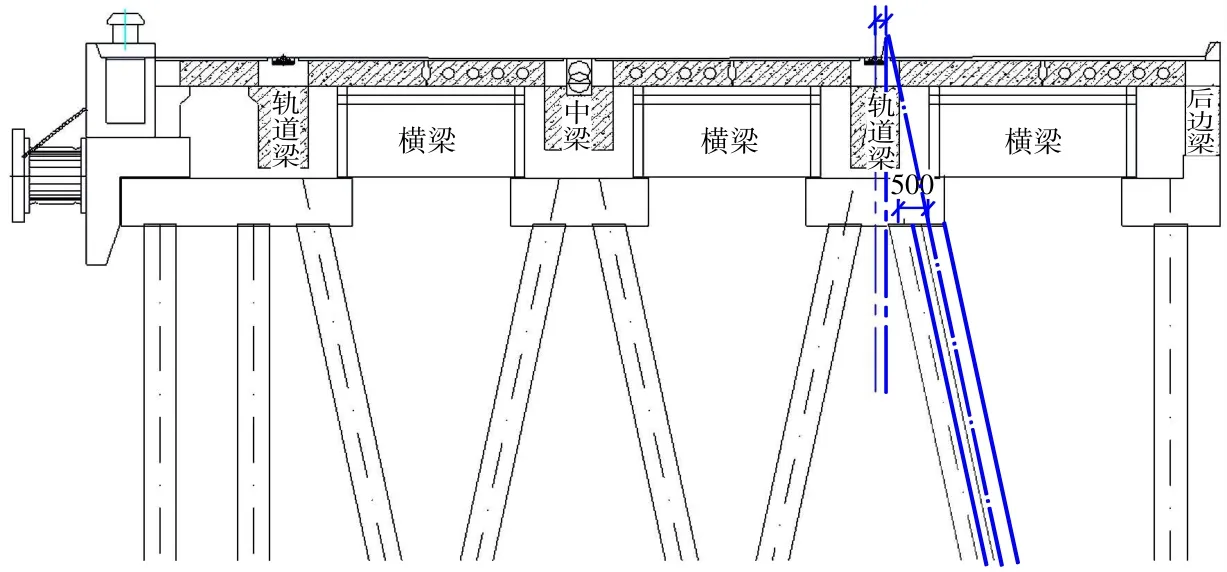
图2 桩基偏位断面图Fig.2 Cross section of pile foundation deviation

2 计算原理

力矩分配法[6]是在位移法理论基础上，提出的直接分析超静定结构的方法。它将结构受到外力后能产生位移的节点用相应的假想刚性约束，在刚性约束处就产生不平衡力或力矩，然后逐个放松附件的刚性约束，消除不平衡力或力矩，恢复真实变形状态。这种计算方法是结构计算领域尤其是工程设计过程中的一种重要方法，对未知量不多的平面杆系单元手算方便，可以直接计算出码头横向排架的各杆端弯矩，其结果的精度将随计算迭代次数的增加而提高，最后收敛于精确值。

3 计算边界简化

桩基的线刚度远小于上部结构，故码头边缘的桩基对上部结构约束很小，可以简化为铰接，码头中间的桩基虽然对上部结构约束同样很小，但是由于上部梁系为多跨连续结构，经过几跨传递后可以接近于固结约束。为了简化计算把偏位桩基的计算模型简化如图3。

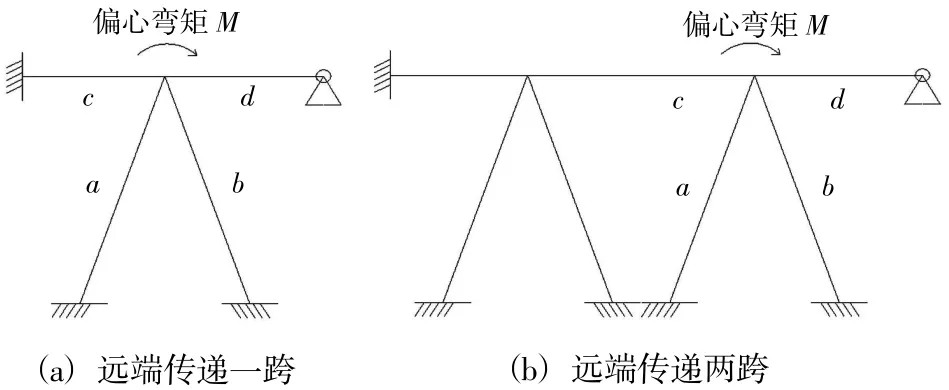
图3 计算简化图Fig.3 Calculation simplified diagram

通过有限元或五弯矩求解法等计算，得到高桩码头在不偏位时各构件的内力和桩基承载力等常规数据[7]。使用期叉桩中斜桩的桩顶最大轴力为1 951.37 kN和599.17 kN。此时斜桩桩头最大的弯矩为-131.52 kN·m，横梁c最大跨中弯矩为301.51 kN·m，横梁d最大跨中弯矩为1312.02 kN·m。

4 简化计算方法

4.1 不考虑施工期影响的偏位计算

1）确定支座的竖向反力

由于叉桩斜度均为5∶1，则其竖向反力等于两个桩基轴力的竖向分力之和，为2 501.01 kN。

2）使用期附加弯矩的确定

由于桩基偏位产生的弯矩为附加弯矩：

3）弯矩分配系数的确定

桩基偏位产生的附加弯矩由偏位节点相邻的各个杆系承担，包含桩基、横梁和面板。由于本工程案例的面板为单向简支板，面板与横梁联系联系薄弱，故在弯矩分配过程中忽略面板的少量有利影响。为便于分析，首先采用远端传递一跨的模型进行计算（见图3）。经计算：

①预应力方桩的截面惯性矩：Ia=Ib=0.014 058 m4，横梁的截面惯性矩：Ic=Id=1.718 5 m4。

②杆系的计算长度：桩基的弯矩计算长度为偏位节点到嵌固点的距离，横梁的弯矩计算长度为偏位节点到相邻纵梁中心点的距离，则La=21.22 m，Lb=19.88 m，Lc=6.25 m，Ld=5.75 m。

③斜桩的弯矩分配系数：远端为固结时，则近端分配4I，远端传递2I；远端为铰接时，则近端分配3I，远端传递0。由于高桩码头远端都接近于固端，所以近端分配均为4I。

同理 μb=0.001 4，μc=0.549 4，μd=0.447 9。

4）分配力矩的确定：Mμ=μM，则Ma=0.83 kN·m，Mb=0.88 kN·m，Mc=343.51 kN·m，Md=280.03 kN·m。

即横梁c的杆端弯矩增加343.51 kN·m，其远端弯矩为343.51/2=171.76 kN·m，跨中弯矩增加（343.51+171.76）/2=257.6 kN·m，横梁d的杆端弯矩增加280.03 kN·m，其远端弯矩为0，跨中弯矩增加（280.03+0）/2=140.02 kN·m。故在不考虑施工期影响的前提下，桩基偏位导致桩基自身弯矩变化0.88 kN·m，横梁c最大弯矩变化257.6 kN·m，横梁d最大弯矩变化140.02 kN·m。

4.2 考虑施工期影响的偏位计算

由于高桩码头的横梁和纵梁等构件往往是预制构件，尺寸不能随意修改，即使桩基发生偏位，桩帽上面的结构也必须按照构件安装图进行正位安装，因此在施工期桩基节点并未浇筑前，会产生一个由自重引起的施工期的附加弯矩值。该弯矩值不会被横梁或面板分配，当不采取补救措施时，只会由桩基进行承担，具体计算方法同不考虑施工期影响的偏位计算。

5 结果与有限元软件的对比

为了准确分析桩基偏位对高桩码头的真实影响，本次模型建立采用Autodesk Robot Structural Analysis Professional有限元中的高桩板壳模块进行空间分析[8]，分析范围为码头的完整结构段60 m×23 m，其中，码头预应力空心板定义为壳单元，为单向简支板，桩基、横梁和纵梁等均采用杆结构单元，各杆结构单元之间的节点默认采用固结连接，桩基与土体作用采用假想嵌固点法，默认桩基在嵌固点处只弹性释放竖向位移。

计算过程中考虑横梁、纵梁、桩基等的真实刚度，由于本工程码头面板设计为单向简支板，面板与横梁连接处并未设置顶层负弯矩钢筋，面板与联系联系薄弱，难以共同受力，故对面板之间的连接根据黄骅四期码头建设实际情况进行局部铰接释放或自由释放，面板在码头结构中仅考虑其传递荷载的功能，忽略其水平刚度。模型图见图4，计算结果对比表见表1。

由于平面理论分析时简化了设计边界条件，结果与有限元分析仍有少量差别。桩基差别较小，能满足设计需要，横梁由于假设一端固结一端铰接，与实际弹性铰结有所差距，误差略大，但基本能够满足工程设计和工程安全的估算需要。

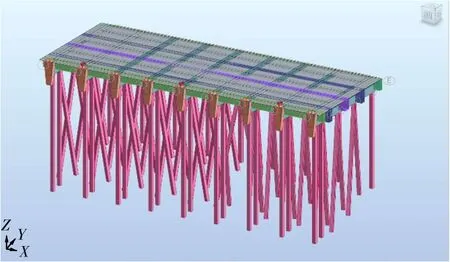
图4 高桩码头整体模型图Fig.4 Overall model of high-pile wharf

表1 平面简化理论分析与有限元空间分析结果对比Table 1 Comparison of the plane simplified theoretical analysis and finite element analysis

6 提高计算精度的方法

根据力矩分配法，通过继续将弯矩向远端分配，多重叠代计算，叠代次数越多，精度越高，偏差率将越小，图5为继续传递一跨的计算过程图，表2为计算结果对比表。

图5 计算过程图（继续传递一跨）Fig.5 Calculationprocedurechart(keeptransmittingaspan)

表2 平面简化理论分析与有限元空间分析结果对比Table 2 Comparison of the plane simplified theoretical analysis and finite element analysis

7 结语

1）平面简化方法随着传递弯矩的增加与有限元空间分析的结果越来越接近，证明了平面简化计算方法能够有效判断桩基偏位对局部桩基弯矩和横梁（或纵梁）甚至面板弯矩的影响。在计算精度要求不高的情况下，采用传递一跨的弯矩分配法，能够快速估算桩基偏位对码头结构承载力的主要影响。

2）一般情况下桩基的线刚度远小于上部联系梁和面板的线刚度，所以桩基偏位产生的附加弯矩，在使用期中会被码头的上部结构承担，分担给桩基的较小。

3）在横纵联系梁的连接节点未浇筑前，结构自重在桩基偏位的情况下会让桩基承受较大的施工期附加弯矩，该附加弯矩会一直存在于使用期中，往往会成为桩基设计的控制弯矩，应该在施工或设计修复中予以重视。有条件的情况下，应该采用相关措施在施工过程中予以消除。