关于“你发现了什么”的认识与思考

刘绪毅 冉茂权

摘  要：人教版小学数学教材中有“你发现了什么”这样一类的习题，老师们在实际教学时由于解读教材不够，对此类习题的编写意图理解不清，往往忽略了它潜在的价值功能，从而影响了学生“四基”的培养和“核心素养”的渗透。文章以三年级教材习题为例，理清“你发现了什么”从哪里来，到哪里去，深化教学的思考与认识。

关键词：小学数学;教材习题;编写意图;探索规律

课后习题是学生数学学习反馈的载体之一，同时也是编者渗透新课标理念的具体体现，它们或是体现某种数学思想，或是渗透某些数学方法，或是蕴含某种数学规律。在现行人教版小学数学教材中，常常会出现这样一类型的习题——“你发现了什么”。老师们在实际教学时由于解读教材不够，对此类习题的编写意图理解不清，往往只追求计算结果，就题论题，而忽视学生过程的经历和思维能力的发展，没有让课后习题发挥其潜在的作用。下面，结合人教版小学数学三年级教材内容，谈谈对“你發现了什么”的认识与思考。

一、从哪里来？——理清编排思路，把握编写意图

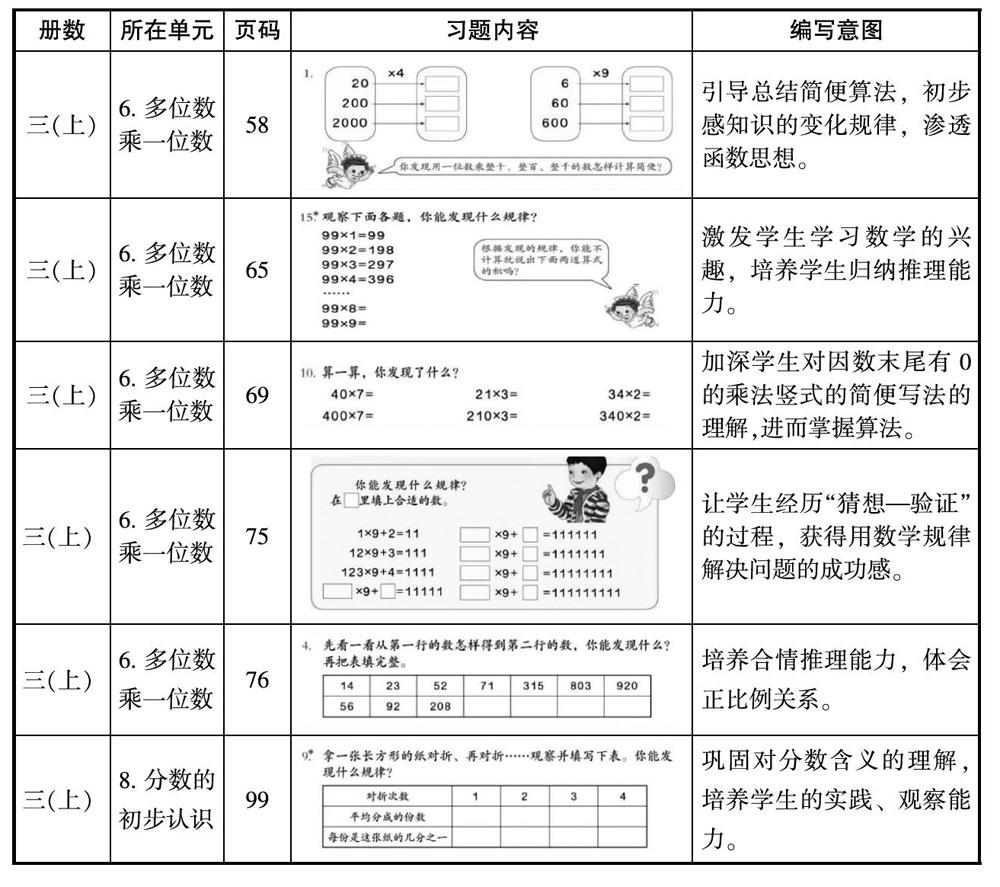
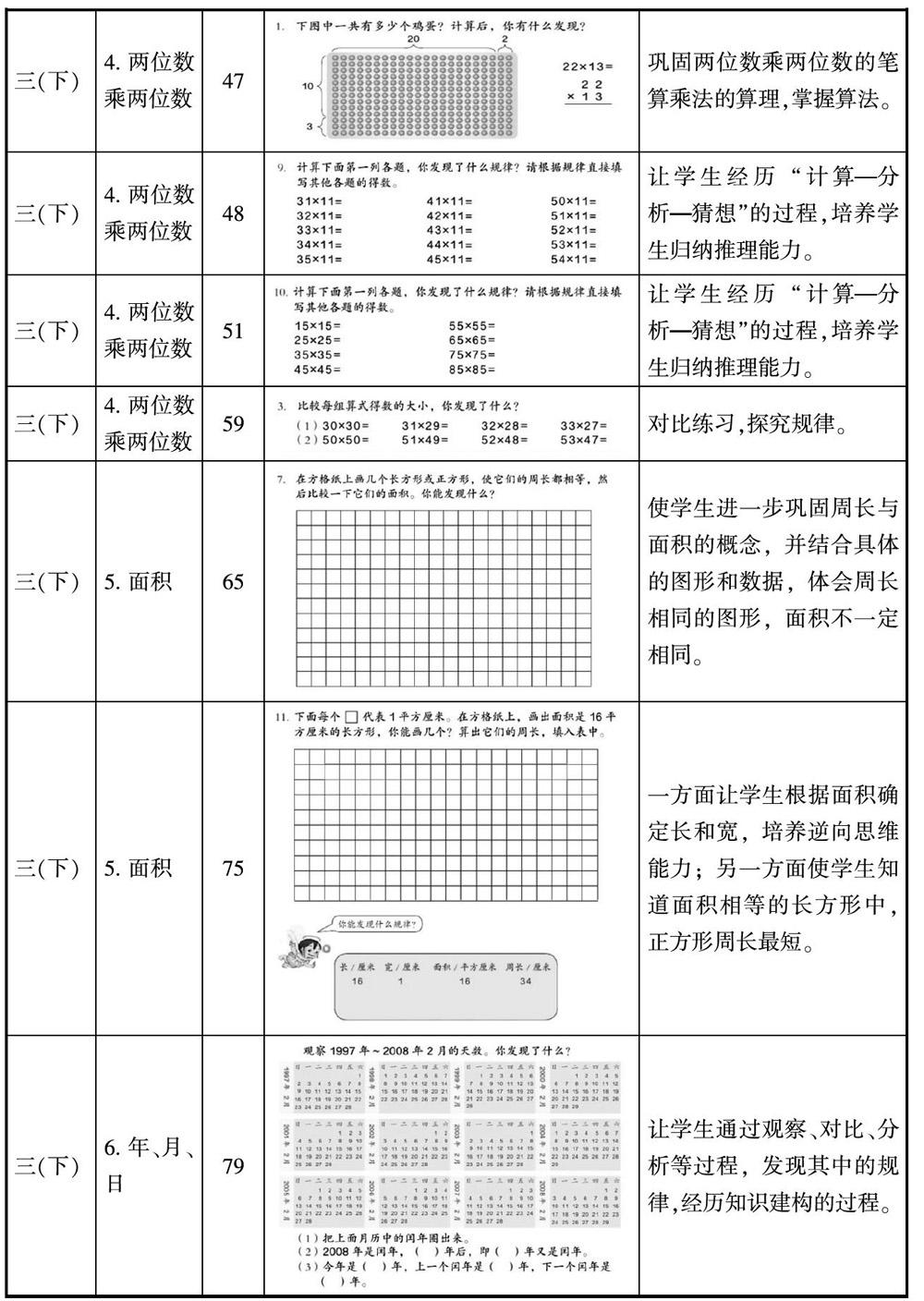
纵观小学数学三年级教材内容，“你发现了什么”在课后习题中共出现13次，其中涉及“数与代数”领域11次，“图形与几何”领域2次。总体上看，不论属于哪一领域，虽然所属章节内容不尽相同，但主要都是以计算内容为主，都需要探索规律。通过这样的编排，一方面对学生所学知识加以巩固提升，加深对数学知识的本质理解;另一方面让学生经历自主探究规律的过程，发展学生的思维能力。具体章节位置及编排意图如表：

二、到哪里去？——挖掘潜在功能，提升综合素养

《数学课程标准》虽然在“数与代数”领域独立设计了“探索规律”的内容，但“你发现了什么”这一类型找规律的内容是以练习题的形式分散编排在教材中，规律隐含在已经认识的数、式、运算或图形里。因此，我们应充分认识并挖掘其潜在的价值功能，为课堂教学中提升学生的综合素养做好补充和发展。

1. 有助于发展数感

小学生正处在由具体形象思维向抽象逻辑思维逐步过渡的阶段，思维能力的提高，数感的形成和发展是一个渐进的过程。在解决“数与代数”领域中“你发现了什么”的时候，使学生经历“计算—分析—猜想”的过程，通过具体计算，发现规律，并获得用数学规律解决问题的成功感，进一步理解了数学知识的本质，也就为发展数感奠定了基础。

2. 有助于提高运算能力

《数学课程标准（2011版）》指出，培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。“你发现了什么”通过对课堂教学内容的补充和延伸，促使学生自主探究规律并应用规律，有助于学生对数学知识的再理解，进一步优化了计算方法，提高了合理简洁运算的能力。

3. 有助于培养合情推理能力

《数学课程标准（2011版）》指出，推理能力的发展应贯穿于整个数学学习过程中。在小学数学教学中，归纳是重要的推理形式，即合情推理。纵观以上13个习题，学生从具体问题出发，都需要探究出其中的规律，而分析、总结规律的过程就是从特殊到一般的合情推理的完整过程。这样学生就经历了归纳推理的全过程，获得了推理的活动经验，提高了学生归纳思维的水平。

4. 有助于积累数学活动经验

《数学课程标准（2011版）》指出，数学活动经验需要在“做”的过程和“思考”的过程中积淀，是在数学学习活动过程中逐步积累的。教学中，通过放手让学生探索规律，学生有足够的时间去经历观察、猜测、计算、推理、验证等活动过程，从而获得丰富的活动经验。

三、如何行动？——夯实教学过程，发展思维能力

基于此类型习题的价值功能，在日常教学中，我们应该充分解读教材，把握编排意图，严格按照“探索规律”的一般模式展开教学活动，注重自主学习与合作学习相结合，让学生经历知识建构的全过程。以三年级上册65页第15题（99乘几）为例，结合学校的“和声课堂”模式谈谈这类习题教学时的行动策略。

（一）观察发现，聚焦疑点

师：同学们，在我们的数字大家庭中，有一些非常神奇的魔法数，今天我们要聊的这个魔法数是99。请仔细观察，这一组算式有什么特点？

生1：这些算式都是99乘几。

生2：第一个因数都是99，第二个因数从1开始乘，第几个算式就乘几。

师：谁能更简洁地说说？

生3：第一个因数都是99，第二个因数依次增加1。

师：如果老师让你算出它们的积，你会全部笔算吗？

生：不会，我猜想它们肯定是有规律的，我会先算出前面几道题，再看看是什么规律。

师：想法不错，你们觉得呢？

【思考】观察是思维的基础。通过谈话激趣，引导学生观察题目特点，为再次观察和探索规律埋下伏笔。并设置疑点，让学生猜想规律，自我完善学习方法，促使学生主动地参与到探究活动中来。

（二）交流总结，寻求突破

师：请先算出前面4题的结果。

课件出示：99×1=99，99×2=198，99×3=297，99×4=396。

师：认真观察这四个算式的乘数和积，你能发现发现什么规律？观察后把你的想法分享给小组内的其他小伙伴。

生小组交流，师巡视指导。

全班汇报：

生1：从积的各位上的数来看，如果把99乘1的积的百位看成0，积百位上的数依次加1，十位都是9，个位下的数依次减1。

师：是这样吗？一起检验一下。还有不同的想法吗？

生2：我们组发现：99乘1等于100-1，99乘2等于200-2，99乘3等于300-3，99乘4等于400-4。

生3：我们小组发现99×1=（100-1）×1，99×2=（100-1）×2，99×3=（100-1）×3，99×4=（100-1）×4，99乘1等于100-1，99乘2等于200-2，99乘3等于300-3，99乘4等于400-4。

师：用一句话怎么说？

生2：99乘几就等于几百减几。

生3：我们组发现：把99分成两个9，一个9写在积的十位上，另一个9与后面的乘数相乘的积的两个数分开写到9的两边，但乘1时百位上不写。

生4：99×a=（100-1）×a=100×a-a。

师：你明白他的意思吗？验证一下。

【思考】让学生从具体问题出发进行数字计算，探索规律法则，学生经历了“计算—分析—猜想—验证”的归纳推理的全过程，获得归纳思维的活动经验，发展了学生的思维能力。

（三）应用提升，达成共识

师：同学们观察得真细致，一下找到了3种不同的规律。你能用规律直接填写出剩下的结果吗？

交流汇报：99×8=792，99×9=891。

师：刚才我们研究的是99乘一位数，如果是99乘11，上面的三种规律都适合吗？验证一下。

生：如果是乘两位数，第一种和第三种方法就不行了，只有第二种方法还适用。99乘11就等于11个100减11。

生：还可以直接用因数是11的简便算法：“两边拉，中间加”。

师：也就是99乘几就等于几个百减几。为什么乘几就会少几？

生：因为99比100少1，乘了几就相当于乘了几个百还少了几个1。

师：同学们真聪明，你能创造一个规律出来吗？

生：我通过刚才的学习发现，99乘几就等于几个百减几，999乘几就等于几个千减几……

【思考】应用规律解决最后两题后，不能满足于表面的规律，还要拓展思维空间，探索规律深层次的原因，达成共识后让学生创造规律，进一步提升学生的思维品质。

总之，深度钻研教材是备好课和上好课的前提，而充分地挖掘课后习题的价值功能，应是钻研教材必不可少的一个环节。上好“你发现了什么”此类型的习题课，更是培养学生“四基”和渗透学科核心素养的一个重要组成部分。