正则化遗传算法下的结构损伤识别研究

滕祯昳，蒋 华

（西华大学，四川成都 610039）

0 引言

近年来土木工程事故的发生频率较大，造成了较大的经济损失和严重的人员伤亡。采用正则化遗传算法，准确全面地识别工程项目中的一些结构损伤问题，将能为全面增强工程项目建设效果提供良好前提。本文采用实验设计方法、调查分析方法，研究了在正则化遗传算法下如何开展结构损伤识别工作，以充分有效地识别工程结构中出现的损伤情况，并及时加以修整，提升工程结构的总体稳定性和安全性。

1 正则化遗传算法的内涵

遗传算法，由上世纪60年代Holland教授提出，其中主要是利用了达尔文进化论，从优胜劣汰的进化原则出发，寻找到下一代中的最优个体，从而得到满足良好要求的最优解。遗传算法在实际应用过程中，为适应现实问题的求解需求，朝着正则化的方向改进。使用结构测量数据的方式，识别实际损伤情况，这一点从数学层面上分析，是反问题的求解过程。但是需要注意到的是，反演问题的时候都表现出较强的不适定性。反问题研究逐渐增多，推进了正则化方法的良好应用。通过遗传算法，针对展平泛函极值问题进行求解能够得到良好效果，其能有效减少损伤识别反问题求解中所受到不适定性的影响，并且在确定目标函数和搜索空间的前提下，就能够实现求解复杂问题的目标。但是，其搜索到接近于最优解的时候，速度较低，且无法获取到最终结果。因而使用遗传算法设置目标函数时，需要将正则化方法下的展平泛函作为基础，而反求得到的近似解则是搜索参数。从而开展层层的搜索求解，评价反求得到的参数，并对其偏差函数急性计算，看其是否在所允许的误差范围内。

2 正则化遗传算法在识别结构损伤中的应用优势

面对工程结构实际运用过程中所出现的不同程度损伤情况，需要充分关注到其实际动力参数的变化情况。根据动力参数的动态特性和结构动力的响应情况，开展识别工作，将能够起到良好的效果。这种做法反映在数学层面上是求解反问题的过程，使用有限元模型修正技术，将能够起到良好的优化效果。想要在这类数学问题中得到准确的答案，需要使用到全局性的搜索方法，遗传算法的总体运行效率较高、搜索速度较快，能够针对一些复杂性的非线性问题进行良好的处理，将其积极有效地应用在结构损伤识别问题中，可以得到较为准确的结果。开展遗传算法损伤识别工作的过程中，需要从不同种群反复计算结构的情况出发，重点结合结构的模态参数和动力响应，通过有限元计算的方式实现目标[1]。想要有效降低计算过程中的负担，使用多项式模型作为良好代表的响应面方法，将其和遗传算法进行充分有效地结合，这样将能很好地修正结构模型。同时需要注意到的是，结构损伤参数反演计算环节，计算过程中所拥有的强不适定性将会影响到结果的准确性，主要是识别结果振荡情况。面对这种情况，使用正则化方法进行良好的处理，将能有效避免这类问题的出现，在正则化遗传算法下的结构损伤识别工作，将能具备较好的鲁棒性，增强损伤识别的精度[2]。

3 正则化遗传算法的应用

遗传算法实际应用过程中，能够有效推进各项计算活动的顺利开展，强化计算结果的准确性。首先，损伤识别活动。通过有限元模型中的局部单元刚度折减实现模拟目标。在表示第个单元的损伤参数时，可以使用α，具体表示情况为α=1使用Ei和Ei0表示出第i个单元出现损伤前后材料弹性的模量。结构单元损伤识别工作中，多是依靠结构振型相关固有动力特征，计算出损伤参数情况的函数，由此修正模型时，需要针对目标函数进行优化。

其次，设立响应面模型。针对结构损伤识别问题进行求解，使用遗传算法将能起到良好效果。设置种群的过程中，可以将结构各个单元的损伤参数作为基础，并按照不同种群，计算出各个结构动力响应情况，这样将能为后续计算适应度函数提供重要的前提基础。这一系列步骤需要引入相应的有限元计算方式，切实提升遗传算法的优化效率，发挥响应面方程的作用，构建起合理性的代理模型，减少大量有限元模态分析计算，从而有效提升计算的总体效率[3]。响应面方法本质上是隐式极限状态函数，其是由一个简单的显式函数逐步逼近实际情况而实现的，能开展不同情况的建模和分析工作，更好地适应不同情况下的响应数据，尤其是当这些响应数据容易受到较多变量影响时，更能够发挥切实有效的作用。在拟合响应量、自变量的过程中，通过高阶多项式模型能够发挥有效作用，更能准确地表述出两者之间的非线性关系[4]。同时，针对响应面模型拟合结构中各项数据的非线性关系，比如说节点振型值、结构单元损伤参数[5]，开展处理活动能够起到良好效果。合理选择和构造样本点，是开展结构模态分析工作的重要前提和基础，使用拉丁超立方体开展抽样工作，是实现样本点构造目标的良好途径，从样本点的各项数值出发，将能提升结构模态分析的总体效果，保证各个样本点所对应的数值形成归一化振型值，在此基础上使用最小二乘法，做好各个样本点的拟合工作，并控制好与样本点相对应的振型值，从而将能明确响应面的具体方程，为后续样本点数值的良好应用提供重要支撑[6]。

再者，需要从正则化的具体实施情况，开展遗传算法的应用活动。当工程项目结构运行过程中出现一些局部性的损伤情况，一般情况下只有这些局部受到损伤情况的单元才会出现结构刚度折减的现象，其他部分都是保持着损伤参数为零的状态。按照数学层面进行思考，这种情况表明，开展结构损伤问题的求解活动，就能够发现其能得到的解在分布状态上呈现出明显的稀疏性[7]。重点分析解的稀疏性，就能够发现其表现出了结构局部损伤识别问题的总体特点，因而能作为重要的先验信息，开展引入活动，从而将能够针对反问题求解过程中出现的不适定性情况进行良好的改善[8]。

4 正则化遗传算法在实际工程案例中的应用

某工程项目中梁全长为12m，将其划分为10个梁单元，其材料密度为7600kg/m3，而弹性模量则为200GPa，惯性矩为1.1×10-4m4，梁本身的横截面面积为0.005566m2。在模拟工程项目中梁的结构损伤情况时，可以从单元的刚度折减出发，从不同单元弹性模量更为细致地模拟出结构出现损伤问题的实际状态。为了保证数值模拟的准确性和真实性，可以将噪声加入到有限元模型的模态分析中，将其作为重要的实测数据。具体采用的振型数据增加噪声的公式为φ=φ0（1+εR），使用表示噪声水平，而加入噪声前后的质量归一化振型值，则需要使用φ0和φ进行表示，R则表示在[-1，+1]范围之内的正态分布中的随机性变量数据。针对梁的结构损伤情况进行计算，主要是采用简支梁中从第3节点到第10节点之间的振型值，针对噪声所带来的不同程度影响进行细致分析，可以将不同水平的噪声添加到振型数据之中，比如说0.5%和1%。经过检测，能得到损伤情况数据，如表1所示。

表1 工程项目简支梁结构损伤工况表

全方位识别梁在不同情况下的损伤情况，将正则化遗传算法作为识别方式，将能够起到良好效果。结合上述三种损伤工况在0.5%噪声水平的识别结果，可以得出以下情况，如图1、图2、图3所示。

5 结语

开展工程项目运行过程中结构损伤情况的识别工作，能及时有效地解决工程项目施工过程中存在的不良问题，保证工程项目的总体建设和运用水平。将正则化遗传算法作为结构损伤识别工作的重要方式，更好地适应了结构损伤各项数据的算法需求，从而起到良好的应用效果。按照正则化遗传算法的各项要求，开展一系列的结构识别和检测工作，将能提升结构损伤识别的准确性。

图1 加正则化项前后损伤识别情况（工况一）

图2 加正则化项前后损伤识别情况（工况二）

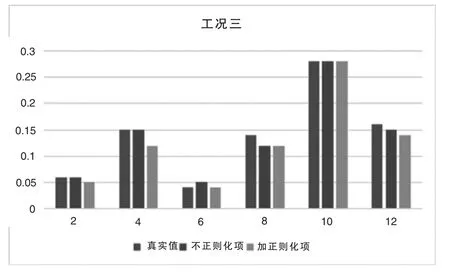
图3 加正则化项前后损伤识别情况（工况三）