函数背景下双变量问题的解决策略之统一变量

■河南省洛阳市汝阳县第一高级中学 张海涛

双变量问题是近年高考数学导数部分压轴题目的常客，在2010年天津、2011年辽宁、2013年湖南、2016年全国Ⅰ卷理科、2018年全国Ⅰ卷理科等高考数学试卷中均以压轴级别出现，在函数与不等式、导数知识的交汇地带，利用导数这个工具，可以充分考查函数及不等式知识，也可以全面深刻地考查高中数学函数思想，充分暴露同学们的探索能力，因此高考命题专家热衷于在这个背景下命制压轴题目。

揭开问题的层层面纱，我们发现解决问题的法宝是构造一元变量函数。下面我们就常见问题进行探究，希望通过本文能给同学们带来帮助。

一、主变量构造统一变量

例1已知0≤m＜n，试比较en-m+ln(m+1)与1+ln(n+1)的大小，并给出证明过程。

分析：本题涉及两个变量m，n，这里不妨把m当成常数，设定n为主变量x。

解：构造函数f(x)=ex-m+ln(m+1)-1-ln(x+1)，x∈[m，+∞)，m≥0。

f(x)min=f(m)=0。

因此，当0≤m＜n时，f(n)=en-m+ln(m+1)-1-ln(n+1)＞0。

所以en-m+ln (m+1)＞1+ln(n+1)＞0。

点评：当问题有两个变量时，我们可以把一个变量看成常数，另一个变量看成自变量，使问题得以解决，我们称这种方法为主变量思想。

二、值域宽度统一变量

例2已知函数f(x)=ax+x2-xlna(a＞0，a≠1)。

(1)求函数f(x)的单调区间;

(2)对∀x1，x2∈[-1，1]，|f(x1)-f(x2)|≤e-1恒成立，求实数a的取值范围。

分析：对于第二问，我们很容易发现问题实际上是求解给定区间上函数的最值的差问题，进而通过求解最值，构造最值的差函数，利用导数求解a的范围即可。

解：(1)函数f(x)的定义域为R，f'(x)=axlna+2x-lna=2x+(ax-1)lna。

令h(x)=f'(x)=2x+(ax-1)lna，则h'(x)=2+axln2a。

当a＞0，a≠1时，h'(x)＞0，所以h(x)在R上是增函数。

又h(0)=f'(0)=0，所以f'(x)＞0的解集为(0，+∞)，f'(x)＜0的解集为(-∞，0)。

故函数f(x)的单调增区间为(0，+∞)，单调减区间为(-∞，0)。

(2)问题等价于f(x)在[-1，1]的最大值与最小值之差小于等于e-1。

由(1)可知f(x)在[-1，0]上递减，在[0，1]上递增，所以f(x)的最小值为f(0)=1，而最大值是f(-1)，f(1)中较大的那个。且f(-1)=+1+lna ，f(1)=a+1-lna，f(1)-f(-1)=a--2lna。

故对 ∀x1，x2∈ [-1，1]，|f(x1)-f(x2)|≤f(1)-f(0)=a-lna。

则a-lna≤e-1。

由a-lna≤e-1，可得a的取值范围是1＜a≤e。

点评：对于任意性、存在性双变量函数值差的问题，根据特征常常可以转化为最值问题进行解决，即构造关于值域的有关函数，我们称之为值域宽度问题。

三、分离构造统一变量

例3已知函数f(x)=(a+1)lnx+ax2+1(a≤-2)，证明:对任意x1，x2∈(0，+∞)，f(x1)-f(x2)≥4x1-x2。

分析：由题中所证结论入手，发现需要证明f(x2)+4x2≥f(x1)+4x1，根据特征构造函数，利用函数单调性证明结论即可。

解：由题意知a≤-2，f(x)的定义域为(0，+∞)，且f'(x)=+2ax=

则f(x)在(0，+∞)上单调递减。

不妨假设x1≥x2，那么|f(x1)-f(x2)|≥4|x1-x2|等价于f(x2)-f(x1)≥4x1-4x2，即f(x2)+4x2≥f(x1)+4x1。

从而g(x)在(0，+∞)上单调递减，故g(x1)≤g(x2)，即f(x1)+4x1≤f(x2)+4x2。

故对任意x1，x2∈(0，+∞)，总满足|f(x1)-f(x2)|≥4|x1-x2|。

例4已知函数f(x)=x2-8x+alnx(a∈R)。

(1)当x=1时，f(x)取得极值，求a的值并判断x=1是极大值点还是极小值点;

(2)当函数f(x)有两个极值点x1，x2(x1＜x2)，且x1≠1时，总有3x1-)成立，求t的取值范围。

分析：对于第二问根据函数在定义域内有两个极值点x1，x2(x1＜x2)，问题转化为t(x)=2x2-8x+a=0在(0，+∞)上有两个不等的正实数根，得到0＜a＜8，。因为变量x1，x2独立性不强，不能直接构造，所以转化为x1的函数解决。

解：(1)f'(x)=(x＞0)，f'(1)=0，则a=6。

(2)函数f(x)的定义域为(0，+∞)，有两个极值点x1，x2(x1＜x2)，则t(x)=2x2-8x+a=0在(0，+∞)上有两个不等的正实数根，所以0＜a＜8。

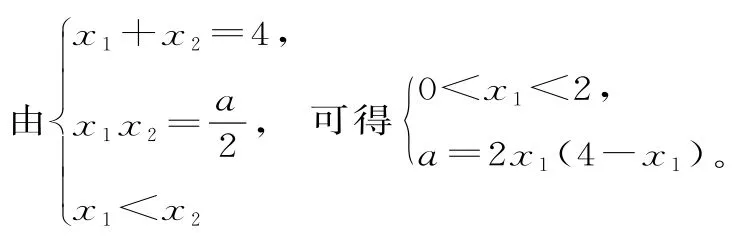
从而问题转化为当0＜x1＜2，且x1≠1

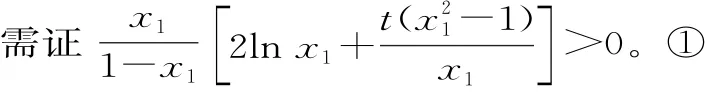
1)当t≥0时，h'(x)＞0，则h(x)在(0，2)上为增函数。但h(1)=0，①式在(1，2)上不成立。

2)当t＜0时，方程tx2+2x+t=0的Δ=4-4t2。若Δ≤0，即t≤-1时，h'(x)≤0，所以h(x)在(0，2)上为减函数。且h(1)在区间(0，1)及(1，2)上同号，故①式成立。

若Δ＞0，即-1＜t＜0时，y=tx2+2x+t的对称轴x=-＞1。

综上可知，t≤-1满足题意。

点评：对于双变量问题，若两个变量地位均等，相互独立，能分离，则分离构造一元函数；不能分离，则合二为一，构造一元函数。

四、齐次式构造统一变量

例5已知f(x)=xlnx-mx2-x，m∈R。若f(x)有两个极值点x1，x2，且x1＜x2，求证:x1x2＞e2(e为自然对数的底数)。

分析：由于题中两个变量x1，x2独立性不强，所以可通过两边取对数转化为证明lnx1+lnx2＞2。由导函数对应方程的根x1，x2，可得通过两个式子的减加得到关于x1，x2的齐次式。这样我们可以通过换元，设，构造一元变量函数解决问题。

证明：欲证x1x2＞e2，需证lnx1+lnx2＞2。若f(x)有两个极值点x1，x2，即函数f'(x)有两个零点。又因为f'(x)=lnxmx，所以x1，x2是方程f'(x)=0的两个不同实根。

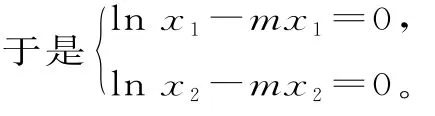
于是ln x1+ln x2=

又0＜x1＜x2，可设，则t＞1。

因此，lnx1+ln

要证lnx1+lnx2＞2，即证2，其中t＞1。

所以h(t)在(1，+∞)上为增函数。

由于h(1)=0，因此，h(t)≥h(1)=0。

点评：对于齐次构造解决极值点偏移的二元变量问题，常常通过对导函数对应的零点方程相减，进而结合需要对导函数的零点方程相加，方便构造出对应两个零点的齐次方程，顺其自然消去参数，结合所证构造对应函数解决问题。

五、切线法统一变量

例6已知函数f(x)=lnx+(e-a)·x-2b，若不等式f(x)≤0对x∈(0，+∞)恒成立，求的最小值。

分析：问题可转化为lnx≤(a-e)x+2b恒成立。设(x0，y0)为曲线y=lnx上的任意点，求解切线方程得到lnx≤x+lnx0-1，利用系数相等得到进而构造关于x0的函数，求解最值即可。

解：由题意知lnx≤(a-e)x+2b恒成立。

设函数y=lnx上一点为(x0，y0)，则x+lnx0-1。

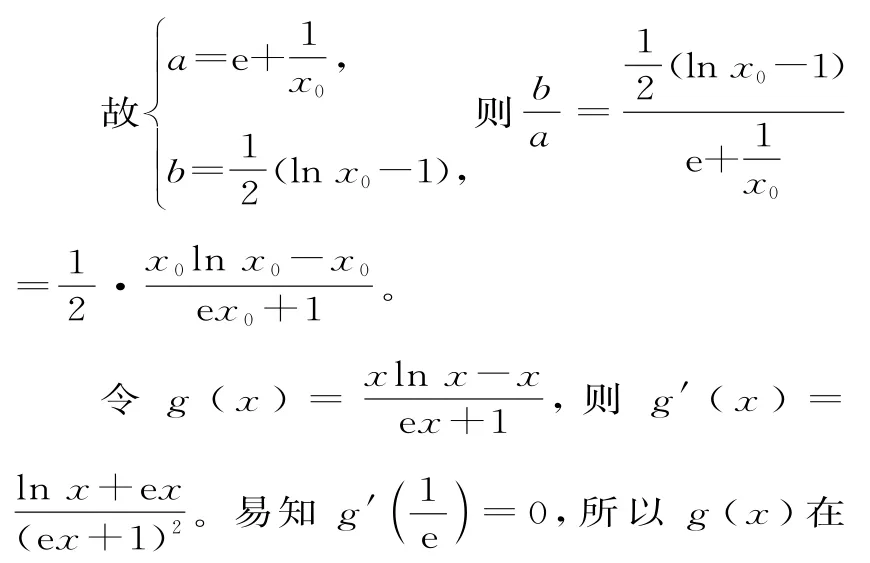
分析：由题意知可转化为ex≥(a+2)x+b-2恒成立。设直线与指数函数的切点坐标为(x0，ex0)，同上，可得到=1-x0，构造函数解决。

解：由题意知ex≥(a+2)x+b-2恒成立，可构造函数f(x)=ex，y=(a+2)x+b-2。

设直线与指数函数的切点坐标为(x0，ex0)，k=f'(x0)=ex0。

所以切线方程为y=ex0·x+ex0-x0ex0，则ex≥ex0·x+ex0-x0ex0。

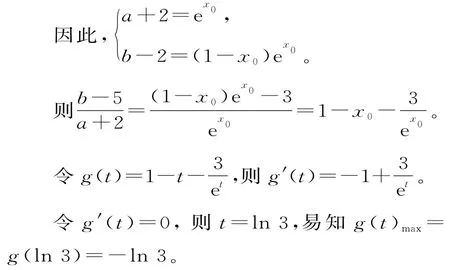
点评：当然也可以转化为f(x)=ex-(a+2)x+2-b≥0恒成立，再转化为f(x)≥f(x)min=0，得到b-5=(a+2)-(a+2)·ln(a+2)-3，因此，=1-ln(a+2)-。令a+2=t，构造函数g(t)=1-2)，求解最大值。

总之，将不等式转化为两个函数的不等关系，辅助以几何关系，如常见的ex≥x+1，ln

x≤x-1等，直观分析曲线间的位置关系，再利用公切线解决问题。

六、对称构造统一变量

例8已知函数f(x)=xe-x(x∈R)。

(1)求函数f(x)的单调区间和极值;

(2)如果x1≠x2，且f(x1)=f(x2)，证明x1+x2＞2。

分析：对于第二问，可构造辅助函数F(x)=f(1+x)-f(1-x)，利用其单调性易知F(0)=0，进而得到F(x)＞0(x＞0)，即f(1+x)＞f(1-x)，然后进行代换即可。

解：(1)易得f(x)在(-∞，1)上内是增函数，在(1，+∞)上内是减函数。

(2)令F(x)=f(1+x)-f(1-x)=(1+x)e-(1+x)-(1-x)ex-1，则 F'(x)=x[ex-1-e-(1+x)]。

当x＞0时，F'(x)＞0，F(x)在(0，+∞)上单调递增。

故F(x)＞F(0)=0⇒f(1+x)＞f(1-x)。

不妨设x1＜1＜x2，则f(x1)=f(x2)=f[1+(x2-1)]＞f[1-(x2-1)]=f(2-x2)。

因为x1＜1，2-x2＜1，且f(x)在(-∞，1)上单调递增，所以x1＞2-x2，x1+x2＞2。

例9已知函数f(x)=(x-1)e1-x。

(1)求曲线y=f(x)在点(1，f(1))处的切线方程。

(2)若函数f(x)与函数y=x2-4x+m(m∈R)的图像总有两个交点，设这两个交点的横坐标分别为x1，x2。①求实数m的取值范围;②求证:x1+x2＞4。

分析：(1)根据导数的几何意义求得切线的斜率，再由点斜式得切线方程。(2)①两个函数作差后构造新函数，这个新函数的最大值大于0，即可解得实数m的范围;②不妨设x1＜2＜x2，则4-x2＜2，且函数g(x)在(-∞，2)上单调递增，欲证x1+x2＞4，只需证明g(x1)＞g(4-x2)，而g(x1)=g(x2)，所以只需证明g(x2)＞g(4-x2)，然后作差构造函数证明其最小值大于0即可。

解：(1)由已知得，则，f(1)=0。又因为f'(1)=1，所以曲线y=f(x)在点(1，f(1))处的切线方程为y=x-1。

(2)①令g(x)=f(x)-x2+4x-m=(x-1)e1-x-x2+4x-m，则g'(x)=-(e1-x+2)(x-2)。

由g'(x)＜0得，x＞2;

由g'(x)＞0得，x＜2。

易知x=2为g(x)的极大值点。

当x→-∞时，g(x)→-∞，当x→+∞时，g(x)→-∞，故当x＜2时函数g(x)有负值存在，在x＞2时也有负值存在。

由题意知，只需满足g(x)max=+4-m＞0，则m的取值范围是m＜+4。

②由题意知x1，x2为函数g(x)=f(x)-x2+4x-m=(x-1)e1-x-x2+4x-m的两个零点。由①不妨设x1＜2＜x2，则4-x2＜2，且函数g(x)在(-∞，2)上单调递增。

欲证x1+x2＞4，只需证明g(x1)＞g(4-x2)，而g(x1)=g(x2)，所以只需证明g(x2)＞g(4-x2)。

令H(x2)=g(x2)-g(4-x2)(x2＞2)，则H(x2)=(x2-1)e1-x2+(x2-3)ex2-3。

故H'(x2)=(x2-2)(ex2-3-e1-x2)。因为x2＞2，所以=e2x2-4＞1，即ex2-3-e1-x2＞0。

所以H'(x2)＞0，即H(x2)在(2，+∞)上为增函数，H(x2)＞H(2)=0。故g(x2)＞g(4-x2)成立，所以x1+x2＞4。

点评：对于比较复杂的双变量函数问题，直接分析往往不容易得手，所以常常进行对称构造解决问题，常见的处理方法为：对于x1+x2＞2m(＜2m)(f'(m)或f″(m)=0)，构造辅助函数F(x)=f(x)-f(2m-x)，结合求导，x1，x2的范围，求解不等式即可；对于x1x2＞m2(＜m2)(f'(m)=0或f″(m)=0)，可构造函数F(x)=f(x)-进行解决；对于其他复杂形式的偏移问题常常通过转化为基本类型，再构造函数解决。

以上就双变量问题进行了简单的归纳讨论，对于平时的双变量问题主要是确定主元问题，恒成立与能成立问题的值域问题、通过分离转化构造函数问题、偏移问题及切线问题，解题的关键是如何转化，所以对双变量问题辨析问题的结构是首要问题，选取方法是解决问题的重要途径，变量归一是解决问题的最终目标，细节操作是实现目标的重要手段。