不同运行方式对高速地铁气动效应的影响
冉腾飞,梁习锋,熊小慧
不同运行方式对高速地铁气动效应的影响
冉腾飞1, 2, 3,梁习锋1, 2, 3,熊小慧1, 2, 3
(1. 中南大学 交通运输工程学院,轨道交通安全教育部重点实验室,湖南 长沙 410075;2. 中南大学 轨道交通安全关键技术国际合作联合实验室,湖南 长沙 410075; 3. 中南大学 轨道交通列车安全保障技术国家地方联合工程研究中心,湖南 长沙 410075)
为了研究时速140 km/h高速地铁列车以不同运行方式在隧道中运行时的气动效应,采用三维、可压、非定常N-S方程的数值计算方法,对地铁列车由明线驶入隧道及站间运行时产生的气动效应进行数值模拟,分析不同运行方式对高速地铁隧道气动效应的影响。研究结果表明:列车站间运行时,车体表面测点压力峰峰值沿车长方向基本不变;而列车由明线驶入隧道时,车体表面测点压力峰峰值从头车向尾车逐渐降低。2种运行方式下的隧道壁面测点压力峰峰值均在中间风井处达到最小值。并且列车由明线驶入隧道时的最大车体表面和隧道壁面压力峰峰值分别为列车站间运行时的1.37倍与1.49倍。不同列车密封指数下,列车由明线驶入隧道时的车内压力变化均大于列车站间运行时的车内压力变化。因此,地铁列车由明线驶入隧道时的空气动力学效应比站间运行时更加不利。
高速地铁;运行方式;气动效应;站间运行;中间风井;压力波;数值模拟;密封指数
地铁隧道的运行环境十分复杂,在运行过程中,地铁列车需要不断地在车站间启动加速与制动停车,并多次驶入与驶出隧道,以便在地下线路与高架线路间转换。列车运行速度的改变会引起隧道内压力变化,隧道入口及中间风井处隧道截面的突变会引起隧道内压力剧烈波动。由于隧道内压力波动幅值和列车运行速度的平方近似成正比[1],因此列车运行速度的提高也会引起隧道内压力剧烈变化。当剧烈的压力波动传入车内时,会引起乘客耳膜压痛,甚至呕吐,产生乘坐舒适性等问题[2]。因此有必要研究高速地铁列车以不同方式在隧道中运行时的气动效应。本文依托于下一代高速地铁项目的研究,分别对时速140 km/h的下一代高速地铁列车由明线驶入隧道与站间运行时引起的空气动力学效应进行研究。数值计算和试验是国内外学者研究地铁隧道空气动力学问题的主要手段。试验主要分为实车试验和模型试验2类,模型试验分为风洞试验、水槽试验和动模型试验等。但是,由于试验具有经济成本高、操作不便、容易受客观环境影响等特点,大部分研究人员采用数值计算的方法研究地铁隧道空气动力学。王秀珍[3]采用三维数值模拟方法,研究了车速、隧道截面形状和隧道长度等因素对地铁列车气动效应的影响,没有考虑列车站间运行方式对隧道内压力的影响,也没有考虑地铁隧道结构的复杂性和特殊性。祝岚等[4]等利用三维、可压缩和非定常的湍流模型,对S型地铁列车匀速进、出隧道以及在隧道中加减速行驶进行数值计算。车轮飞[5]利用动网格和三维数值模拟方法计算地铁列车通过中间风井时的隧道内压力波动,但是列车最大运行速度为100 km/h,且未考虑列车由明线驶入隧道及加减速的情况。刘伊江[6]计算地铁列车在车站间匀速运行时的隧道内风压,未充分考虑中间风井所引起的气动效应,也没有考虑列车由明线驶入隧道的情况。NIU等[7]计算地铁列车在隧道中的站间运行,却忽略了中间风井对隧道内气动效应的影响。本文借鉴国内外学者对高速铁路隧道空气动力学的研究方法及理论,结合地铁隧道结构的复杂性和特殊性,对高速地铁隧道空气动力学进行研究。利用ICEM CFD对地铁列车与隧道进行结构网格划分,采用可压、非定常N-S方程及−湍流方程的数值模拟方法及滑移网格技术,对时速140 km/h高速地铁列车以不同方式在隧道中运行时的空气动力学效应进行数值计算,得到隧道内和车内的压力变化情况,研究不同运行方式对高速地铁气动效应的影响,并判断哪种运行方式引起的空气动力学效应更不利。
1 运行区间的确定
地铁列车站间运行的速度图如图1(a)所示,运行过程分为起动加速、惰性运行和制动停车3个阶段[8]。为确保数值模拟计算简单、有效,可以将列车的站间运行过程看成匀加速运行、匀速运行和匀减速运行[7],如图1(b)所示。其中启动加速、匀速运行和制动减速的加速度分别为1=1 m/s2,2=0 m/s2,3=−1 m/s2。
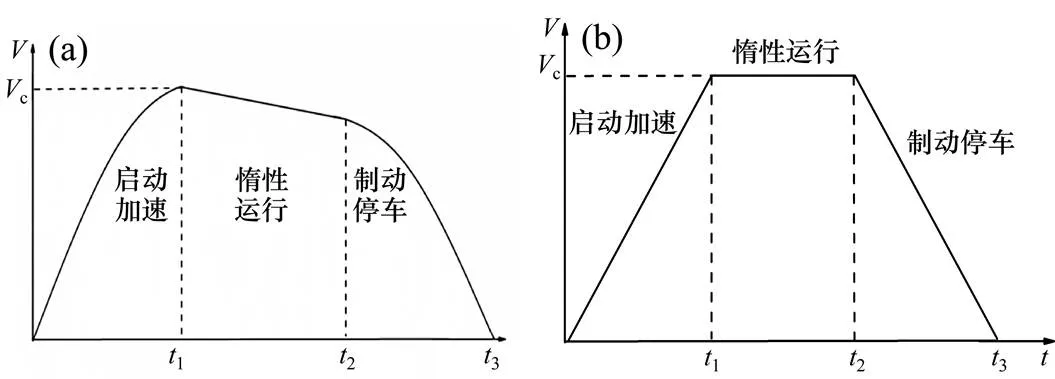
(a) 站间运行速度图;(b) 站间运行简化速度图
为了对比分析地铁列车站间运行与匀速驶入隧道过程中的气动效应,地铁列车经过中间风井时需保持匀速运行(即惰性运行)。因此,可以将地铁列车的运行区间设置为最短运行区间的基础上适当增加列车惰性运行区间,具体分析如下。
当地铁列车的惰性运行时间为0时,可以计算得到列车站间运行的最短运行区间长度为:
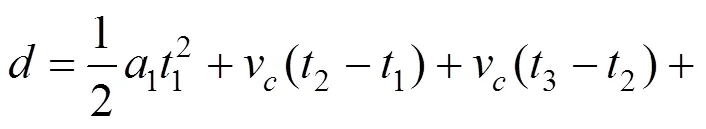
其中:1=1 m/s2,2=−1 m/s2,v=140 km/h=38.89 m/s,1=2=38.89 s,3=77.78 s。
在最短运行区间的基础上,适当增加12.54 s的惰性运行时间,可以计算得到地铁隧道的运行区间长度为:
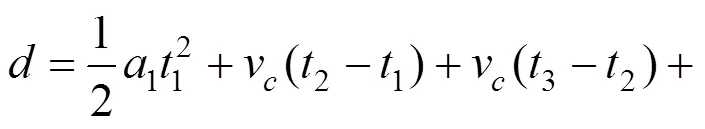
其中:1=1 m/s2,2=−1 m/s2,v=140 km/h=38.89 m/s,1=38.89 s,2=51.43 s,3=90.32 s。
2 计算条件
采用滑移网格法模拟地铁列车在隧道中的运行,计算区域如图2所示。中间风井是在隧道中部预留的通道,主要用于通风、防水,危急时刻也可用于排烟、逃生与消防。为满足地铁隧道环境的通风换气、环控和消防方面的要求,在地铁隧道的普通长区间(大于等于1.8 km)中均需设置中间风井。本文中,列车在隧道中运行的区间长度为2 km,在普通长区间范围内。因此需要在隧道运行区间的中间位置设置矩形截面的中间风井[4],其中,风井壁面的尺寸为4 m×4 m×15 m,风井出口域的尺寸为50 m×50 m×15 m。
为了真实模拟地铁列车驶入隧道洞口的情况,保证列车周围流场充分发展[9],设置车头距离隧道入口50 m,车尾距离流域入口处150 m。
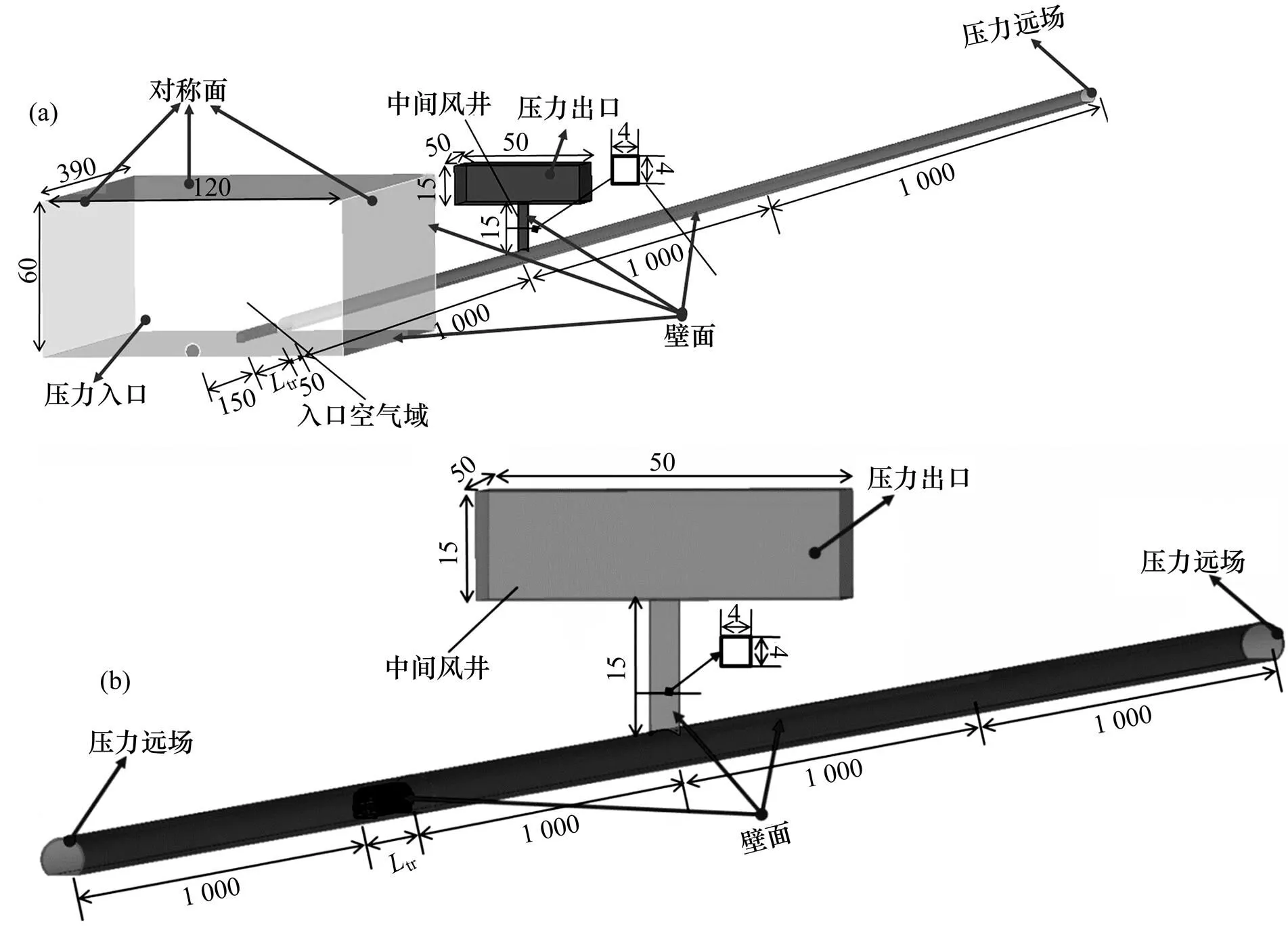
单位:m
地铁隧道长度很大,隧道网络复杂[6],因此,对地铁隧道环境进行了简化。为了模拟地铁长大的隧道环境,避免出口边界受尾流的影响[9],在地铁隧道2 km运行区间的基础上添加1 km长的隧道,如图2所示;同时,为了让隧道出口(列车站间运行时为隧道入口和隧道出口)免受反射波带来的影响,将其设为压力远场P-far[7]。
给定列车运动边界条件:方向速度分量等于列车运行速度=140 km/h,和方向速度分量等于0。流域侧面、顶面给定为对称面symmetry,流域的底面、风井壁面、隧道壁面及地面均给定无滑移边界条件wall。同时,为了使流场得到充分发展,将进口边界条件设为in=0,将风井出口边界条件设为out=0。
数值计算采用的6车编组A型地铁列车如图3所示。图中,对地铁列车的外形进行了简化,忽略转向架、受电弓的影响[11−12]。其中,列车高=3.8 m,宽=3 m,整车长tr=139.5 m,列车横截面面积v=9.785 m2。地铁列车表面共布置10个测点,测点布置情况如图4所示,其中头尾车测点对称布置。
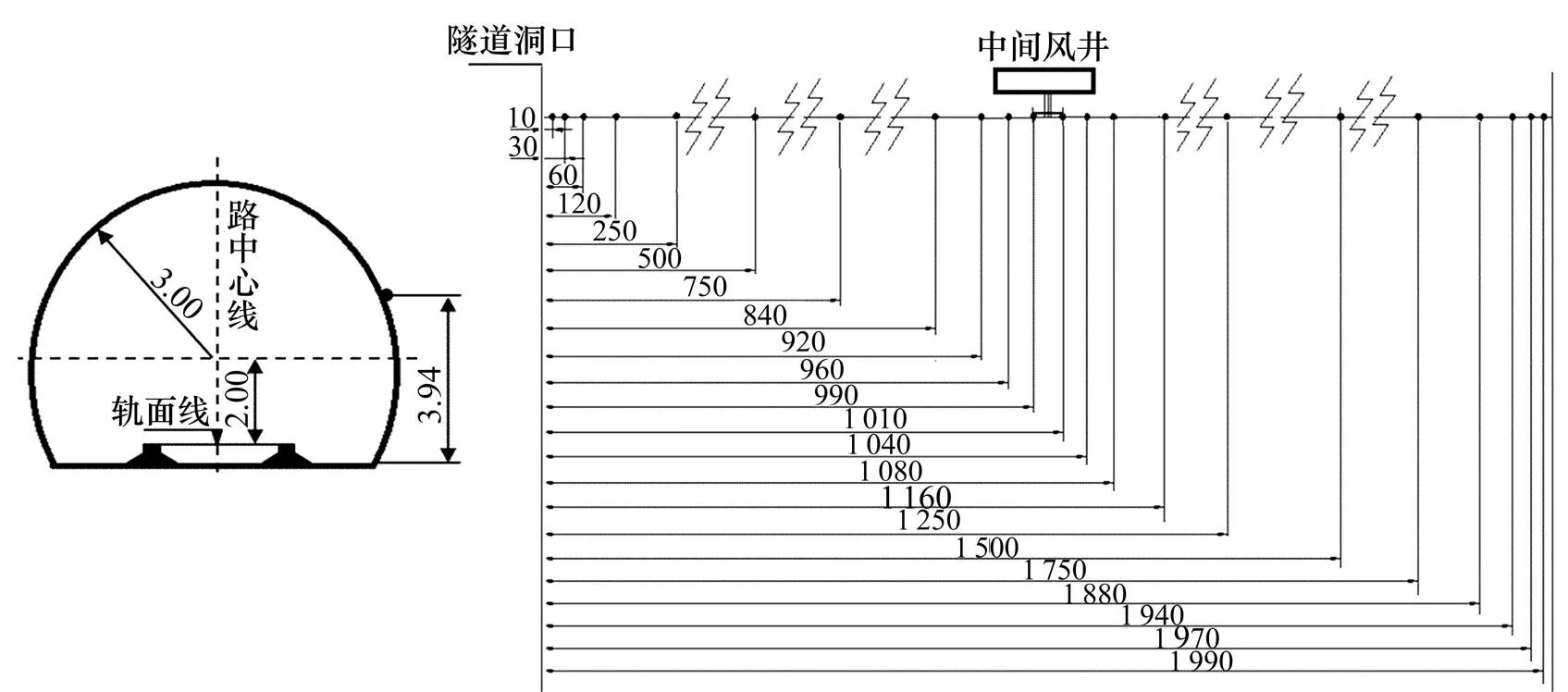
单位:m
数值计算采用的隧道净空断面如图4所示。图中,数值计算采用隧道的盾构直径为6 m,对应的净空断面面积A为26 m2,对应的阻塞比(即列车横截面积与隧道净空断面面积之比)为0.376。
隧道壁面压力测点布置在距离地面3.94 m的隧道壁面上,并在中间风井两侧对称布置,共有22个测点,其分布情况如图4所示。
在CFD计算中,计算网格质量的好坏会直接影响数值计算结果的效率与精度[13],因此,对隧道中的流体区域进行结构网格划分:采用外C网格与O网格将列车壁面、隧道壁面和相应的BLOCK的surface进行映射,建立无厚度壁面;中间风井与隧道连接处的结构类似于T型管,可以划分为三通网格,部分网格划分如图5所示。
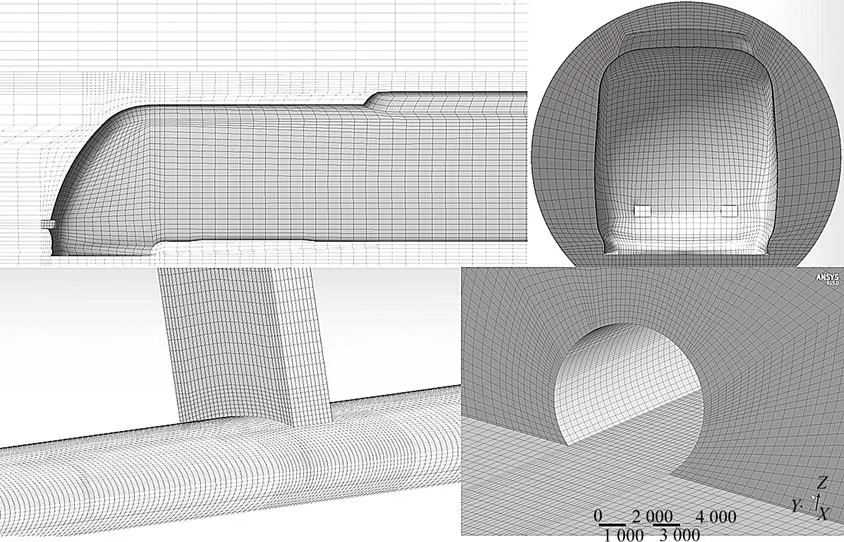
图5 计算网格分布示意图
3 数值算法验证
为验证数值计算结果的正确性与可信度,利用中南大学轨道交通安全教育部重点实验室自主研制1:20缩比的动模型试验装置,对时速100 km/h的地铁列车匀速通过盾构直径为6 m,长度为1 km隧道时的场景进行动模型试验,并进行相同工况的数值计算验证。其中,动模型试验装置的列车和隧道模型如图6所示,数值计算方法为可压、非定常N-S方程与−湍流方程。

图6 动模型试验模型
动模型试验中的测点布置示意图如图7所示。其中,隧道壁面上共布置6个测点,车体表面上共布置6个测点。
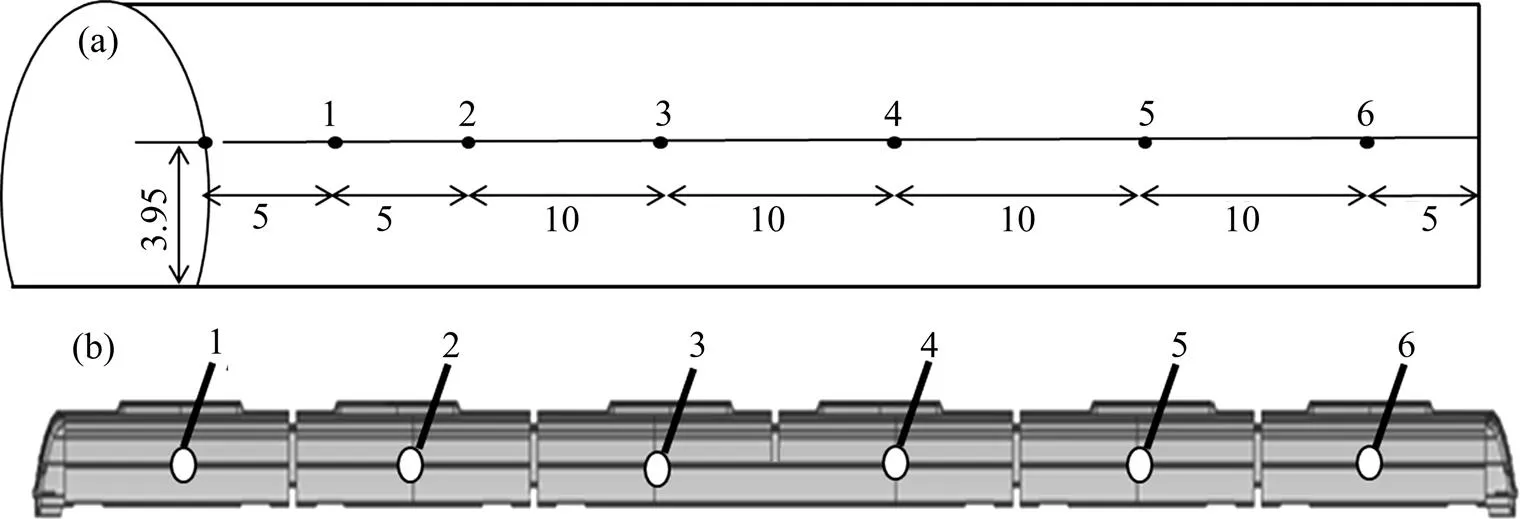
单位:m
数值计算与动模型试验中的车体表面2号测点和隧道壁面3号测点的压力对比波形如图8所示;相应的测点压力变化的结果对比如表1所示。
从表1中数据可以看出,数值计算所得测点压力的最大值、最小值和峰峰值与动模型试验结果中最大值、最小值和峰峰值的最大差异为5.9%,在数值计算误差容许范围内,从而验证了本文数值计算方法的正确性与可信度。
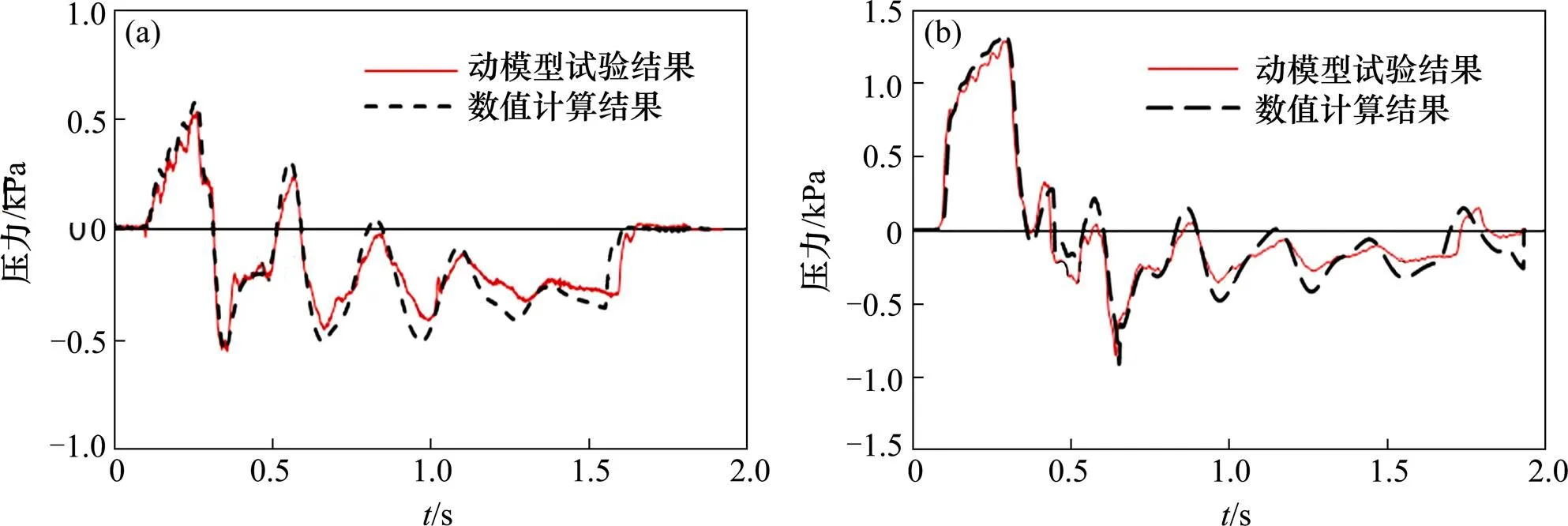
(a) 车体表面2号测点;(b) 隧道壁面3号测点

表1 压力变化结果对比
4 列车在隧道中运行时气动效应研究
分别对地铁列车站间运行和由明线驶入隧道时的隧道内和车内气动效应进行对比分析,研究不同运行方式对高速地铁气动效应的影响。
图9和图10分别为列车站间运行和由明线驶入隧道时,不同时刻隧道内的压力分布云图,其中列车的运行区间均为2 km。
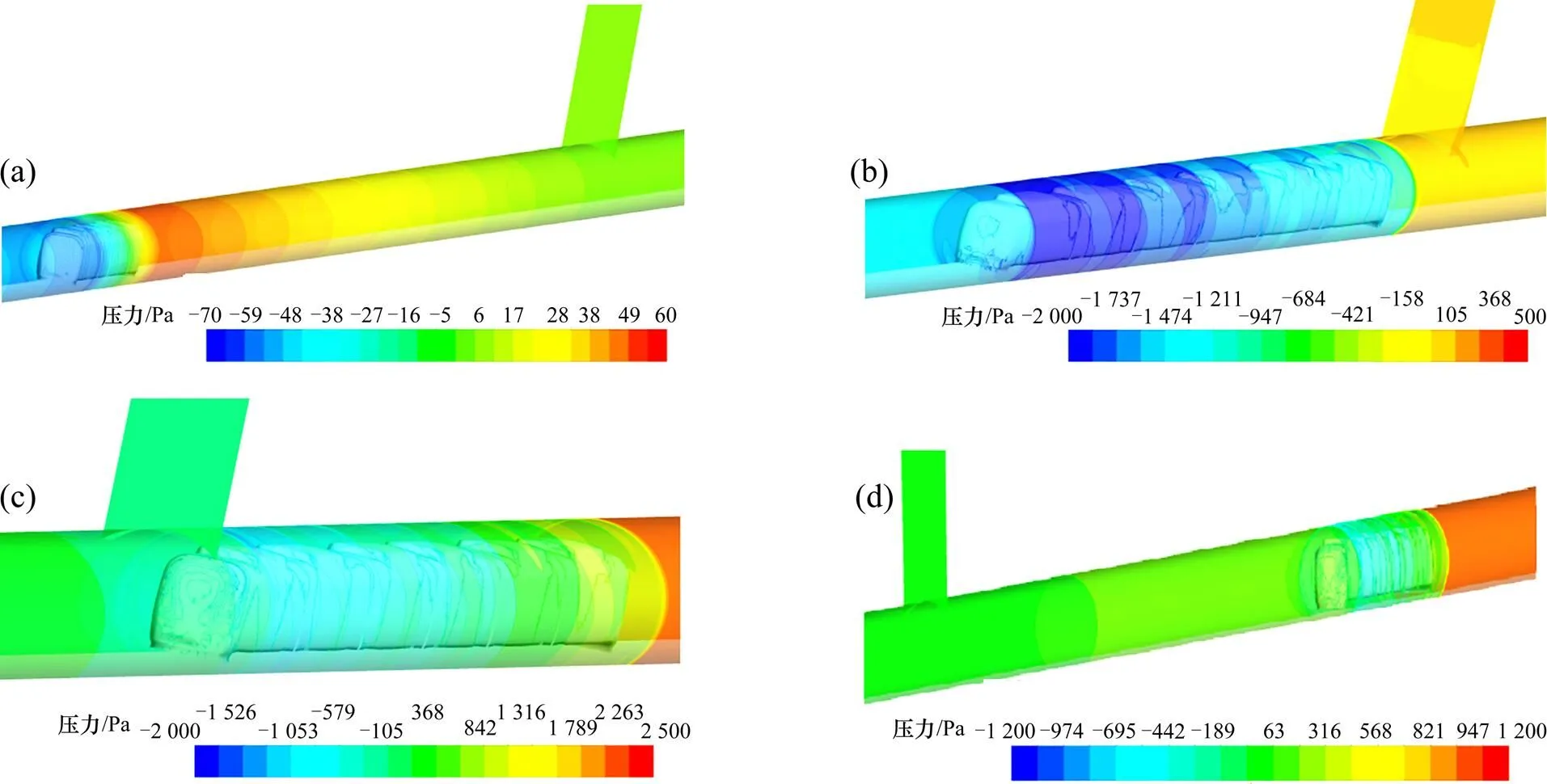
(a) t =2.1 s;(b) t =44.1 s;(c) t =48.3 s;(d) t =58.8 s
从图9可以看出,=2.1 s时,列车启动加速时隧道内压力变化范围很小,中间风井处压力基本无变化。=44.1 s时,列车匀速运行至中间风井前侧,列车速度的提高使隧道内压力变化范围明显增大,其中尾车的车头与车身过渡处负压值达到−1.7 kPa;中间风井处断面突变,导致附近的压力均在0.4 kPa以下。=48.3 s时,列车匀速通过中间风井,头车经过中间风井时会产生压缩波,使隧道内压力增大,其中头车的鼻尖以及相应的隧道壁面正压值均达到2.5 kPa;中间风井断面突变,导致附近的负压至迅速减小至0.4 kPa以下;而尾车通过中间风井后会形成膨胀波,使隧道内压力下降。=58.8 s时,列车减速制动,列车速度的降低导致隧道内压力变化范围变小,中间风井处受列车运动的影响很小,压力基本无变化。
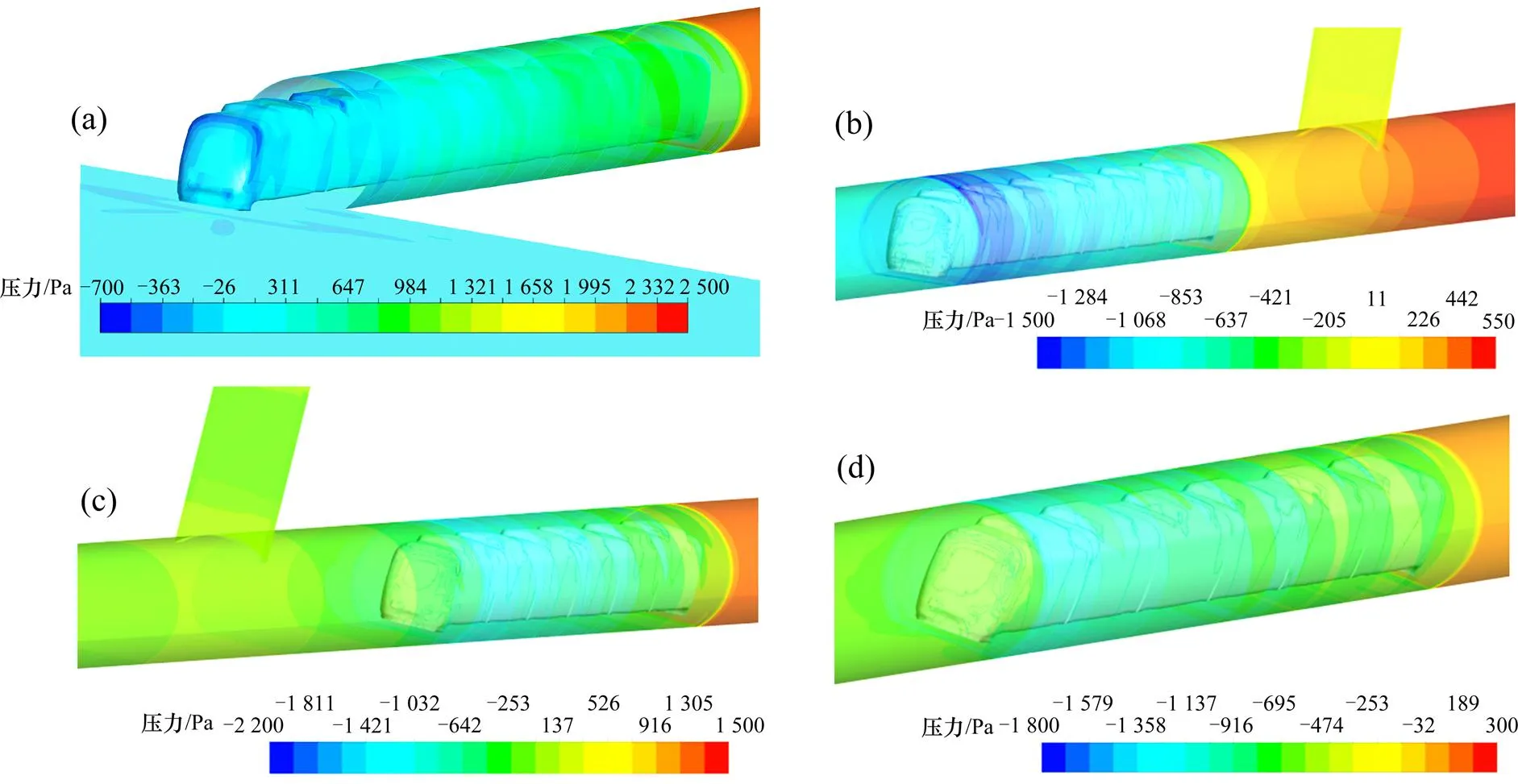
(a) t =4.4 s;(b) t =26.4 s;(c) t =35.2 s;(d) t =58.8 s
从图10可以看出,=4.4 s时,列车头部驶入隧道,头车会形成初始压缩波,使隧道内压力骤增。=26.4 s时,列车在到达中间风井前,由于中间风井断面突变的影响,车体表面和隧道壁面的压力变小,均在0.55 kPa以下。在=35.2 s,列车已经通过中间风井,在头车通过中间风井时会产生压缩波,其以声速在隧道内传播;在尾车通过中间风井后,列车尾部产生膨胀波,压力下降。=58.8 s时,列车继续在隧道中传播,车体表面压力变化范围减小,并且头车及隧道壁面的正压值急剧降低。
4.1 车体表面压力对比
当列车由明线驶入隧道时,由于压力远场的设置,隧道出口没有反射波返回,压力波在隧道入口和中间风井之间不断反射。而列车站间运行时,隧道入口和隧道出口均没有反射波返回,压力波只能在中间风井处反射。
本节选取车体表面2号测点,分析以不同运行方式对车体表面测点压力变化的影响,结果如图11所示。
从图11可以看出,不同运行方式对车体表面测点压力变化的影响很大:在列车匀速驶入隧道的过程中,测点压力的第1次上升①是由于列车头部由明线驶入隧道时产生的初始压缩波传播到车体表面测点引起的。测点压力的第1次下降②是由于列车尾部驶入隧道时,产生的初始膨胀波传播到车体表面测点引起的。测点压力波的第2次下降③是因为初始压缩波在传播时遇到中间风井时,一部分压缩波以膨胀波的形式向隧道入口返回时传播到车体表面测点引起的。这之后,隧道内的压缩波与膨胀波在隧道入口与中间风井之间不断地反射,这些反射回来的压力波传播到车体表面测点,导致测点压力不断变化。列车经过中间风井④时,车体表面测点压力剧烈变化:头车经过中间风井时产生压缩波,导致测点压力迅速增大;列车经过中间风井过程中,中间风井处气流紊乱,导致车体表面压力剧烈变化;尾车经过中间风井时产生膨胀波,导致车体表面测点压力迅速下降。这之后车体表面测点压力变化逐渐趋于稳定。
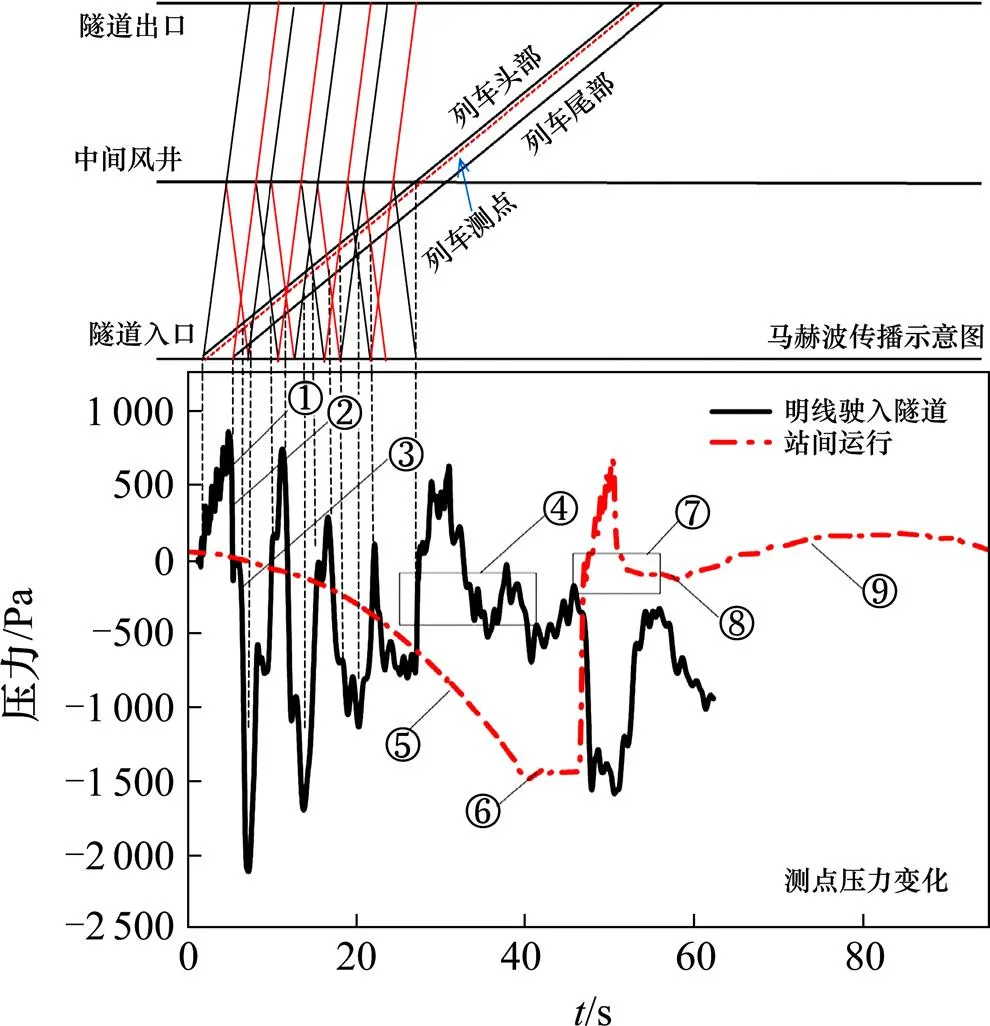
图11 不同运行方式下车体表面测点压力变化曲线
列车站间运行时,在加速运行过程⑤中,车体表面测点主要在负压区波动,并且负压值缓慢降低,这是由于列车启动加速过程中,所引起的压缩波不明显,从而削弱了测点在正压区的波动;列车在时刻⑥开始匀速运行,测点压力基本不变;当列车经过中间风井⑦时,车体表面压力会迅速增大,并剧烈变化;列车通过中间风井后,测点压力迅速减小至0附近,并保持稳定。从时刻⑧开始,列车在隧道内减速运行⑨,由于地铁隧道较长且隧道出口无反射波返回,车体表面测点压力经历较小的正压波动后逐渐趋于平缓。
不同运行方式下沿车长方向的压力峰峰值变化规律如图12所示。其中,距鼻尖距离为车体表面各测点距离鼻尖的水平距离与列车高度的比值,列车高度=3.8 m。从图12可以看出,列车站间运行时,车体表面测点压力峰峰值沿车长方向基本不变;而列车由明线驶入隧道时,车体表面测点压力峰峰值沿车长方向从头车向尾车呈下降趋势;并且列车在驶入隧道时车体表面测点最大压力峰峰值比列车站间运行时的车体表面测点压力峰峰值大37%。因此,地铁列车由明线驶入隧道时车体表面压力变化超过列车站间运行时车体表面压力变化。
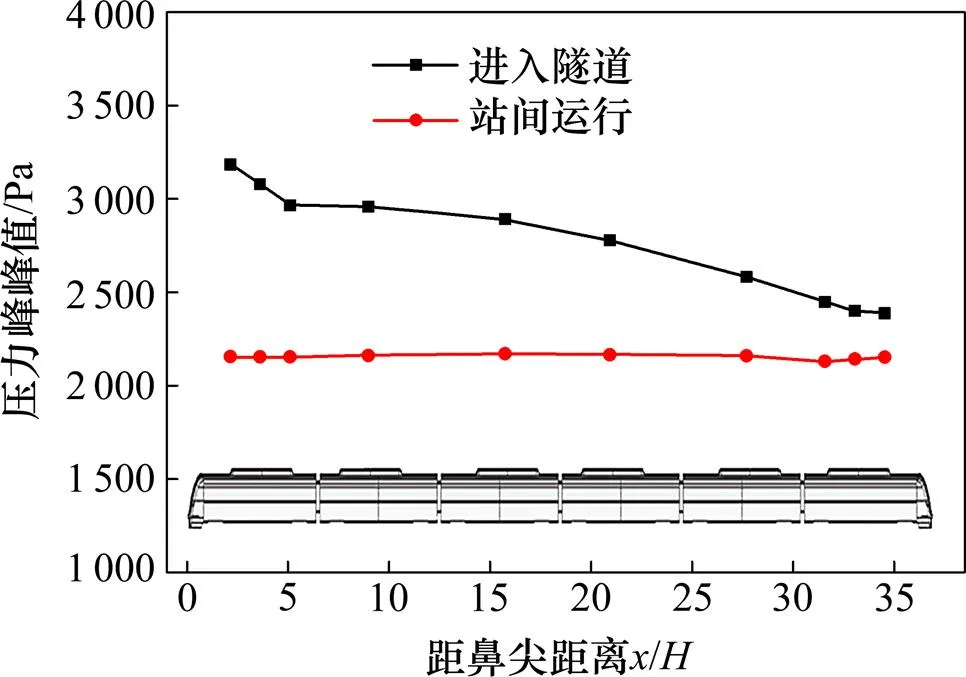
图12 不同运行方式下车体表面测点压力峰峰值变化规律
4.2 隧道壁面压力对比
选取距离列车启动位置500 m处的隧道壁面测点,分析以不同运行方式对隧道壁面测点压力变化的影响,结果如图13所示。
从图13可以看出,不同运行方式对隧道壁面测点压力变化的影响很大:在列车匀速驶入隧道的过程中,测点压力的第一次上升①,是由于列车头部由明线驶入隧道时产生的初始压缩波传播到隧道壁面测点引起的。测点压力第1次下降②,是引起的列车尾部驶入隧道时产生的膨胀波传播到隧道壁面测点引起的。这之后,隧道内的压缩波与膨胀波在隧道入口与中间风井之间不断地反射,这些反射回来的压力波传播到隧道壁面测点,导致测点压力不断变化。列车经过隧道壁面测点③时,隧道壁面测点不断受到列车带来的压缩波与膨胀波,测点压力发生轻微抖动。列车经过风井④时,隧道壁面测点压力剧烈变化,这之后压力变化逐渐趋于 平缓。
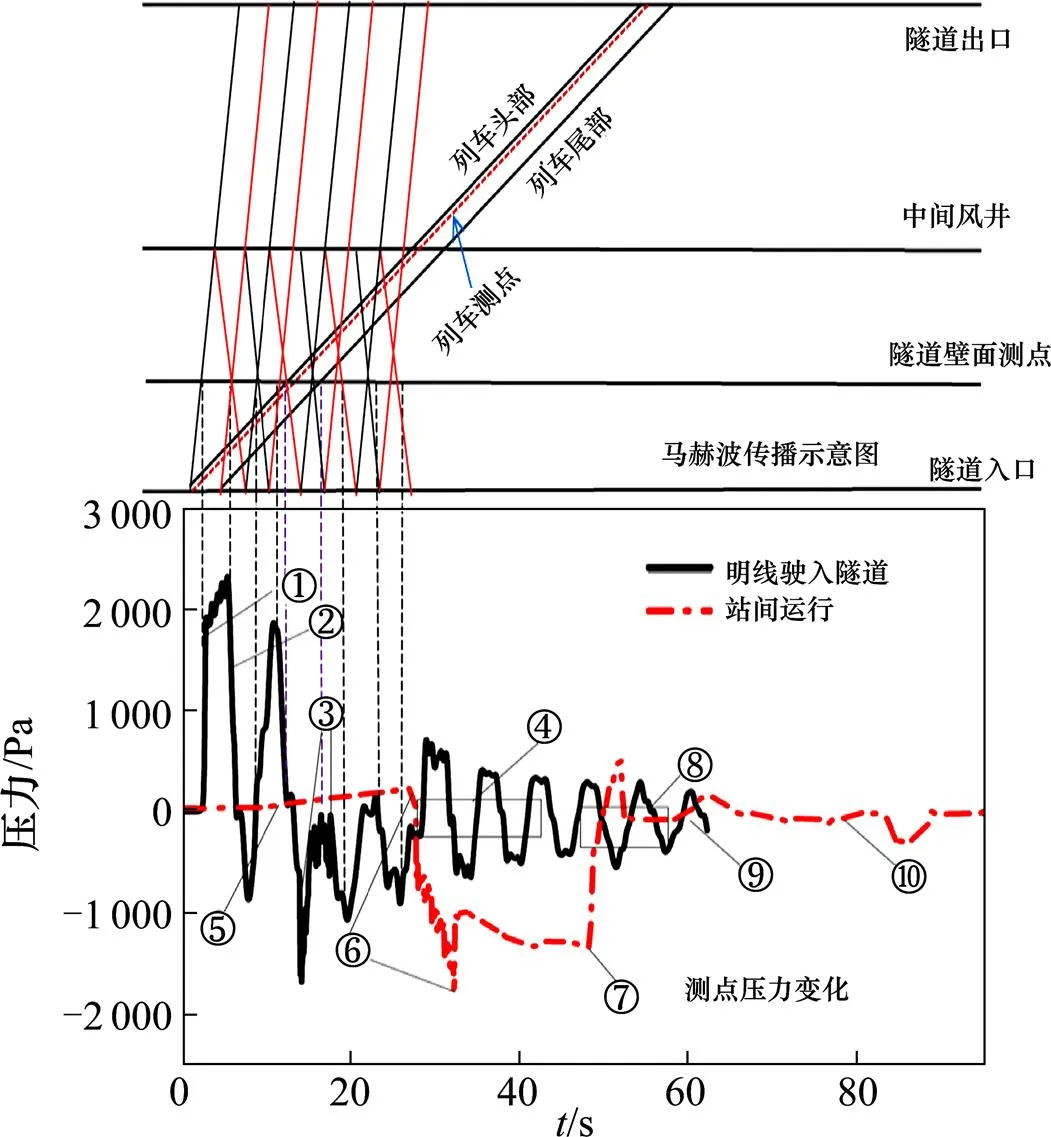
图13 不同运行方式下隧道壁面测点压力变化曲线
列车站间运行时,在加速运行过程⑤中,测点在正压区产生微小波动,这是由于列车在车站启动加速时,产生的压缩波传播到隧道壁面测点引起的;在列车经过隧道壁面测点⑥时,隧道壁面测点压力会发生轻微抖动;在列车在⑦处开始匀速运行,测点压力基本不变化;列车经过中间风井⑧时,隧道壁面压力迅速增大,并发生剧烈变化,在列车通过中间风井后,测点压力又迅速减小至0值附近,并保持稳定。从时刻⑨开始,列车在隧道内减速运行⑩,由于地铁隧道较长且出口处无反射波,列车减速过程中无膨胀波反射回来,隧道测点压力经历较小的负压波动后逐渐趋于平缓。
从图14可以看出,列车以不同运行方式在隧道中运行时,受中间风井处断面突变的影响,隧道壁面测点压力峰峰值在中间风井附近达到最小值,最小值为1.47 kPa左右。列车由明线驶入隧道时,压力峰峰值在距离隧道入口500 m和1 500 m附近达到最大值,为4.83 kPa。列车站间运行时,在距离列车启动位置840 m和1 160 m附近达到最大值,为3.23 kPa。并且列车驶入隧道时的最大压力峰峰值比站间运行时的最大压力峰峰值大49%。因此,地铁列车由明线驶入隧道时隧道壁面压力变化超过列车站间运行时隧道壁面压力变化。
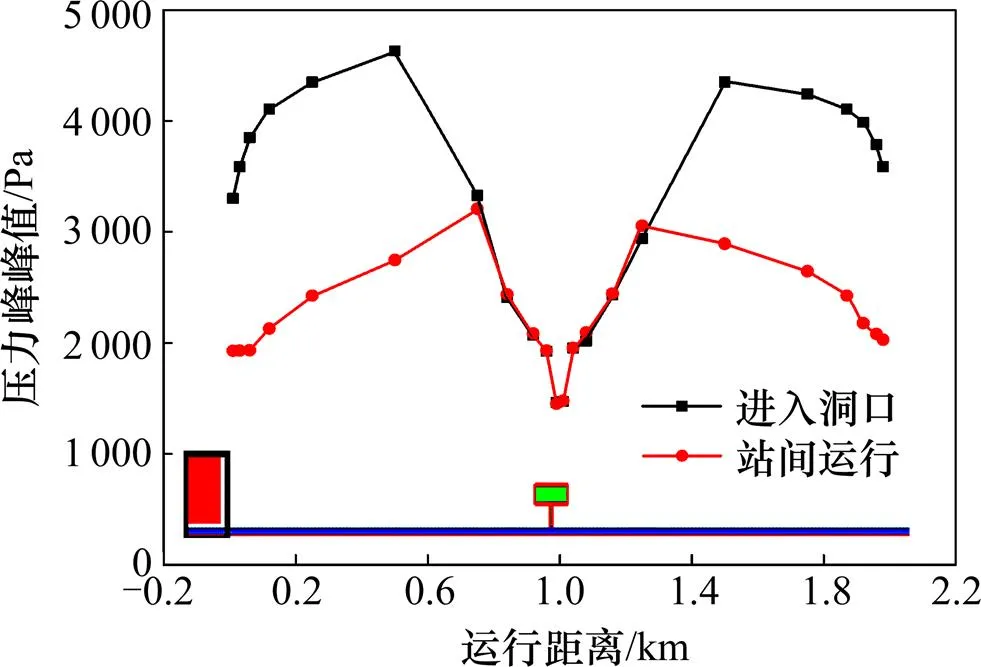
图14 不同运行方式下隧道壁面测点压力峰峰值变化规律
4.3 更不利地铁列车运行方式的选择
车内压力变化是衡量乘客乘坐舒适性的重要指标之一,也是判断空气动力学效应的重要标准。车内压力变化可以由车外压力变化通过相应的迭代公式计算得到。
假定车内压力变化率与车内外压差成正比:
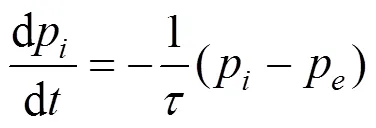
其中:p为车内部压力;p为车外部压力;为列车密封指数。
式(1)可以等效成
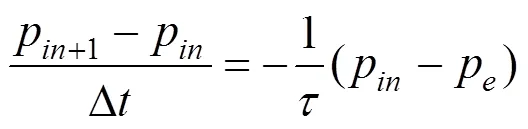
其中:Δ为数值计算过程中的时间步长。
在初始时刻=0 s时,p0=0,式(2)可以等效成
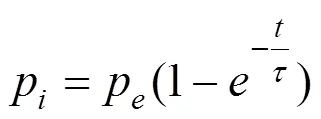
式(3)即为车内压力变化的迭代公式。
当地铁列车的密封指数分别为=0.5 s,=0.7 s,=1.5 s时,将列车以不同运行方式运行时测得的车体表面2号测点对应的车内测点压力变化率和3 s压力变化幅值(即任意3 s内压力变化峰峰值)进行对比分析,结果如图15所示。
从图15可以看出,地铁列车以不同方式在隧道中运行时,车内压力变化差距很大。不同密封指数的地铁列车以不同运行方式在隧道中运行时,车内最大压力变化率和3 s压力变化幅值均沿车长方向从头车向尾车逐渐减小。当密封指数分别为=0.5 s,=0.7 s,=1.5 s时,地铁列车由明线驶入隧道时的车内最大压力变化率分别是列车站间运行时车内压力变化率的1.14倍,1.10倍和1.15倍;3 s压力变化幅值分别是列车站间运行时的1.37倍,1.29倍和1.11倍。因此,地铁列车由明线驶入隧道时车内压力变化超过列车站间运行时车内压力变化。
综上所述,地铁列车由明线驶入隧道时的空气动力学效应比站间运行时更不利。
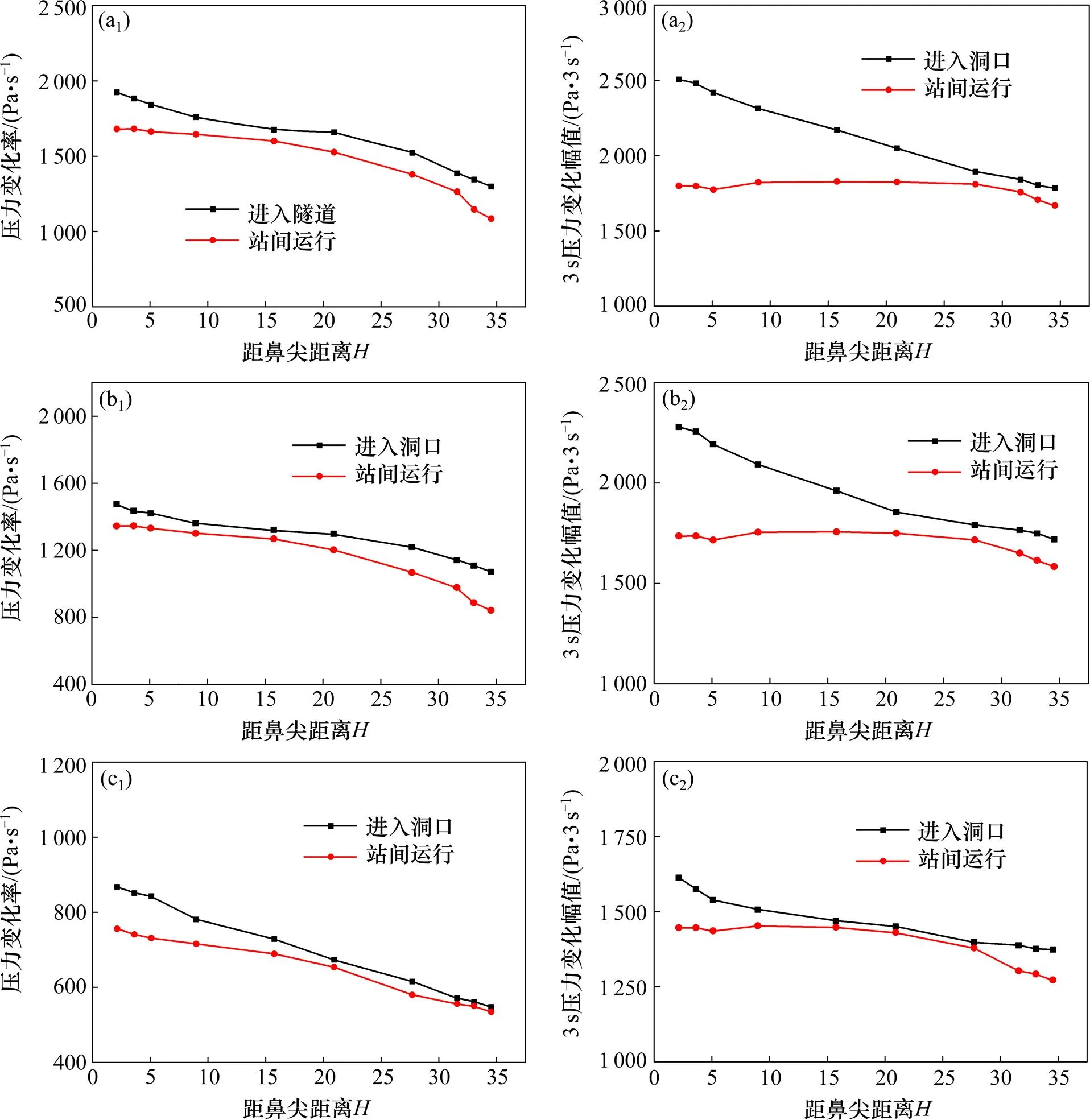
(a1), (a2) τ=0.5 s;(b1), (b2) τ=0.7 s;(c1), (c2) τ=1.5 s
5 结论
1) 列车站间运行时,车体表面压力峰峰值沿车长方向基本不变;列车由明线驶入隧道时,车体表面压力峰峰值从头车向尾车逐渐降低。
2) 不同运行方式下,隧道壁面测点压力峰峰值均在中间风井处达到最小值。
3) 列车由明线驶入隧道时的隧道内压力峰峰值和车内压力变化均超过列车站间运行时的隧道内压力峰峰值和车内压力变化。
[1] 李新华. 高速列车过隧道、会车等典型状态下非定常空气动力学效应研究[D]. 杭州: 浙江大学, 2012. LI Xinhua. Unsteady simulation of a train passing a tunnel and two trains passing by each other[D]. Hangzhou: Zhejiang University, 2012.
[2] 铃木浩明, 高魁源. 车内压力波动引起耳鸣的研究[J]. 国外铁道车辆, 1999(5): 15−18. Suzuki Hiroa, GAO Kuiyuan. A review of research trends on passengers’ aural discomfort caused by rail tunnel pressure change[J]. Foreign Rolling Stock, 1999(5): 15−18.
[3] 王秀珍. 地铁列车气动效应分析[J]. 中国科技信息, 2011(21): 85−86.WANG Xiuzhen. The aerodynamic effect analysis of metro train[J]. China Science and Technology Information, 2011(21): 85−86.
[4] 祝岚, 张东, 孙振旭, 等. 基于乘客舒适性的快速地铁隧道压力波分析[J]. 都市快轨交通, 2015, 28(1): 87−91.ZHU Lan, ZHANG Dong, SUN Zhenxu, et al. Analysis on the pressure wave of rapid subway tunnel based on passenger comfort[J]. Urban Rapid Rail Transit, 2015, 28(1): 87−91.
[5] 车轮飞. 城市地铁隧道中间风井处车箱内瞬变压力模拟分析[J]. 建筑热能通风空调, 2011, 30(3): 89−91.CHE Lunfei. Simulation and analysis of the transient pressure variation of the carriage at the middle ventilation shaft of the urban subway tunnel[J]. Building Energy & Environment, 2011, 30(3): 89−91.
[6] 刘伊江. 高速地铁隧道压力波研究及隧道断面的拟定[J]. 铁道标准设计, 2010(增2): 119−124.LIU Yijiang. Study on the pressure wave of high-speed subway tunnel and the design of tunnel section[J]. Railway Standard Design, 2010(Suppl 2): 119−124.
[7] NIU J, ZHOU D, LIANG X, et al. Numerical study on the aerodynamic pressure of a metro train running between two adjacent platforms[J]. Tunnelling & Underground Space Technology, 2017, 65: 187−199.
[8] 毛励良. 地铁车站合理站间距探讨[J]. 都市快轨交通, 1996(3): 33−37. MAO Liliang.Reasonable station spacing of subway stations[J]. Urban Rapid Rail Transit, 1996(3): 33−37.
[9] Ogawa T, Fujii K. Numerical investigation of three-dimensional compressible flows induced by a train moving into a tunnel[J]. Computers & Fluids, 1997, 26(6): 565−585.
[10] González M L, Vega M G, Oro J M F, et al. Numerical modeling of the piston effect in longitudinal ventilation systems for subway tunnels[J]. Tunnelling & Underground Space Technology, 2014, 40(2): 22−37.
[11] YANG X, JIN J, SHI G. Preliminary study on streamlined design of longitudinal profile of high-speed train head shape[J]. Procedia-Social and Behavioral Sciences, 2013, 96: 1469−1476.
[12] Samane F. Aerodynamic of the trains in tunnels [D]. Birmingham: University of Birmingham, 2014.
[13] 孙帮成, 李明高. ANSYS FLUENT 14.0仿真分析与优化设计[M]. 北京: 机械工业出版社, 2014. SUN Bangcheng, LI Minggao. ANSYS FLUENT 14.0 simulation analysis and optimization design[M]. Beijing: China Mechanical Press, 2014.
[14] CHU C R, CHIEN S Y, WANG C Y, et al. Numerical simulation of two trains intersecting in a tunnel[J]. Tunnelling & Underground Space Technology Incorporating Trenchless Technology Research, 2014, 42(5): 161−174.
[15] XIANG X T, XUE L P. Tunnel hood effects on high speed train-tunnel compression wave[J]. Journal of Hydrodynamics Ser B, 2010, 22(5): 940−947.
[16] WANG Yiwei, YANG Guowei, HUANG Chengguang, et al. Influence of tunnel length on the pressure wave generated by high-speed trains passing each other[J]. Science China Technological Sciences, 2012, 55(1): 255− 263.
[17] 齐江浩, 赵蕾, 王君, 等. 地铁隧道活塞风实测及特征分析[J]. 铁道科学与工程学报, 2016, 13(4): 740−747.QI Jianghao, ZHAO Lei, WANG Jun, et al. Subway piston wind measurement and analysis of Xi’an metro Line 2[J]. Journal of Railway Science and Engineering, 2016, 13(4): 740−747.
[18] 刘希贤, 郭安宁, 梅元贵, 等. 高速铁路复线隧道内压力波特性的数值模拟研究[J]. 铁道科学与工程学报, 2015, 12(1): 20−27. LIU Xixian, GUO Anning, MEI Yuangui, et al. Numerical simulation of pressure wave characteristics generated by a high-speed train passing through a double- track tunnel[J]. Journal of Railway Science and Engineering, 2015, 12(1): 20−27.
Influence of different operation modes on the aerodynamic effect of high-speed subway
RAN Tengfei1, 2, 3, LIANG Xifeng1, 2, 3, XIONG Xiaohui1, 2, 3
(1.Key Laboratory of Traffic Safety on Track (Central South University), Ministry of Education, School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China; 2. Joint International Research Laboratory of Key Technology for Rail Traffic Safety, Central South University, Changsha 410075, China; 3. National & Local Joint Engineering Research Center of Safety Technology for Rail Vehicle, Central South University, Changsha 410075, China)
To research the aerodynamic effect of high-speed trains running with different operation modes in tunnel whose speed is 140 km/h, it simulated aerodynamic problems caused by trains when they enter tunnel from open air and run between stations based on the three-dimensional, compressible and unsteady N-S equation method. The influence of aerodynamic effect with different trains’ operation modes in high-speed subway tunnel was analyzed. The results show: The peak-to-peak value of measurement points on train’s surface is constant along the direction of train length by trains entering tunnel from open air. But the peak-to-peak value of measurement points on train’s surface decreases from head carriage to rear carriage by trains running between stations. The peak-to-peak value of measurement points on tunnel wall is the minimum at the place of middle shaft by trains running with different operating modes. And the maximal peak-to-peak value on train’s surface and tunnel wall caused by trains entering tunnel from open air is respectively 1.37 times and 1.49 times compared with trains running between stations. The pressure changes inside carriages caused by trains entering tunnel from open air is larger than that caused by trains running between stations with different tightness index. As a result, the aerodynamic effect caused by trains entering tunnel from open air is worse than the aerodynamic effect caused by trains running between stations.
high-speed subway; operation modes; aerodynamic effect; running between stations; middle shaft; pressure wave; numerical simulation; tightness index
10.19713/j.cnki.43−1423/u.2019.04.004
U270
A
1672 − 7029(2019)04 − 0860 − 11
2018−04−26
国家科技支撑计划项目(2015BAG12B01-24)
梁习锋(1963−),男,湖南长沙人,教授,从事列车空气动力学研究;E−mail:gszxlxf@163.com
(编辑 阳丽霞)

