考虑地表沉降的盾构隧道掘进参数优化研究

汪高文，高建强

（广东建科建设咨询有限公司 广州510500）

0 引言

近年来，随着我国城市化进程的推进，隧道、地铁建设规模不断扩大，据统计，2017年全国公路隧道增加1 048 处，总长度124.54 万m[1]，城市轨道交通在建里程5 770 km[2]。盾构法因其机械化程度高、围岩扰动少等优点，在隧道施工中得到了广泛的应用。然而盾构掘进造成的地表沉降变形仍无法完全避免，特别是当盾构下穿建筑物、铁路等既有设施时，如果地表沉降过大，将严重影响建筑物或列车的安全。因此在盾构掘进时，根据盾构掘进导致地表沉降的规律，研究掘进参数的控制和优化方法，降低地表沉降，具有重要的意义。

目前针对盾构掘进参数优化控制方面的研究主要集中在两方面，一方面是在不同地质条件下不同掘进参数对围岩变形的影响。魏纲[3]基于Mindlin 解对盾构造成的地表沉降进行了计算，唐晓武[4]在此基础上，补充了刀盘摩擦造成地表沉降的计算公式。张润峰[5]、王海振[6]、余志刚等人[7]则从工程实践出发，分别对在不同地质条件下实测的掘进参数与地表沉降进行关联性分析。另一方面则主要集中在掘进参数的优化措施及方法研究，李超等人[8]采用BP 人工神经网络，建立了复合地层条件下盾构掘进参数的预测模型。郑刚等人[9]在分析盾构掘进参数和对周围地层影响规律的基础上，根据不同参数地表沉降影响敏感度及致险排序，提出盾构掘进引起变形的精细化控制措施。

本文基于盾构掘进对围岩的影响机理，分析了千斤顶推力、刀盘转速和土舱压力等参数对地表沉降的影响，并利用最优控制理论对掘进参数进行优化，以降低掘进造成的地表变形。

1 盾构掘进对地表沉降影响分析

盾构机在掘进时，通过泥水舱或土舱中的泥浆或土体平衡掌子面的水土压力，同时旋转刀盘切割前方岩土体，在千斤顶的驱动下向前顶进，并在后方同步进行管片铺设和注浆。因此，施工过程中围岩受到扰动主要由盾构正面附加推力、刀盘摩擦、盾壳摩擦和盾尾间隙造成（见图1）。

图1 盾构掘进扰动示意Fig.1 Shield Tunneling Disturbance Diagram

1.1 正面附加推力

盾构机在掘进过程中，对岩土体的正面推力主要有泥水舱/土舱压力和千斤顶推力，由于泥水舱/土舱压力主要用于平衡掌子面的水土压力，因此，实际上对围岩造成扰动的正面附加推力大小为

式中：D为盾构机直径；N为千斤顶推力；Pb为泥水舱/土舱压力；qb为掌子面的水土压力。

正面附加推力引起的围岩变形可利用水平集中力作用于弹性半空间的Mindlin 解进行计算[10]。魏纲等人[3]假定正面附加推力为作用在圆形掌子面上的均布荷载，利用Mindlin 解在掌子面上进行积分，求得盾构掘进引起的地面变形。若将均布荷载替换为式⑴表示的实际荷载，则盾构掘进引起隧道轴线上地表某点的竖向变形为：

其中，

式中：μ、G分别为土体的泊松比、剪切模量；x为地表某点离隧道掌子面的轴向距离；h为隧道轴线埋深；R为盾构半径。

1.2 刀盘摩擦

刀盘摩擦主要通过刀盘上辐条和辐条上的刀具施加到围岩上，唐晓武等人[4]通过将单根辐条与围岩的摩擦力分解成水平分量和竖直分量，分别利用Mindlin 解求得各分量引起的围岩竖向变形，最后将所有辐条的变形量相加，得到了刀盘摩擦导致的土体竖向变形为：

其中，

式中：m为刀盘辐条数量；φ为刀盘初始角度；y为地表某点离隧道掌子面的横向水平距离；T为刀盘扭矩。

1.3 盾壳摩擦

盾构在掘进过程中，其外壳与围岩之间的摩擦力也会对围岩造成扰动，设摩擦力沿盾壳均匀分布，其大小为Ps，则根据魏纲等人[3]的研究结果，盾壳摩擦引起的地面沉降为：

其中，

式中：L为盾构长度。

1.4 盾尾间隙

由于盾构机外径略大于隧道管片环的外径，盾构机经过后，将在盾尾留下一定建筑空隙，为降低盾尾间隙对围岩造成的扰动，盾构掘进时将在盾尾进行同步注浆，但仍无法完全消除盾尾间隙的影响，工程中常用地层损失率η来衡量掘进造成的地层的损失，根据李忠超等人[11]的试验结果，地层损失率与正面附加推力存在二次关系：

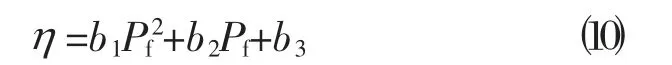
盾尾间隙造成的地表沉降可采用镜像法求得。唐晓武[4]假定地层损失沿隧道轴线均匀分布，并对Sagaseta 镜像法公式进行修正，得到盾尾间隙造成的地表沉降为：

综上，对正面附加推力、刀盘摩擦、盾壳摩擦和盾尾间隙造成的地表沉降进行叠加，得到盾构掘进造成的地表总沉降：

2 盾构掘进参数优化

要对盾构的掘进参数进行优化，需要在所有可行的参数控制方案中，探寻一个最优的组合方案，使盾构机在该方案的控制下进行掘进时，能最大限度地降低其所造成的沉降，因此可将该问题转化为一个最优控制问题进行研究[12]。

若假设盾构沿x轴方向掘进，则盾构掘进时其位置可以用掌子面的x坐标来表示，则盾构掘进速度为掌子面的x坐标对时间的一阶导数。由于掘进速度是多个掘进参数的综合反映，因此，以千斤顶推力N、刀盘转速M和土舱压力Pb等参数为控制变量，结合张厚美[13]通过实验总结出的掘进速度多元线性回归模型，可建立盾构掘进时的系统状态方程为：

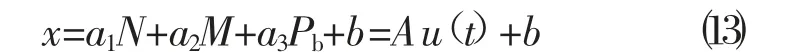
式中：A=（a1、a2、a3）、b为回归系数；u（t）=（N，M，Pb）为控制变量。在工程实际中，各参数均应处于一定合理范围内，因此规定：

以盾构掘进的起点和终点为系统状态的初始和终端条件，则有：

最后确定目标泛函，设地表沉降控制点的坐标为（x1，y1，0），则优化的的目标为降低掘进过程中控制点的沉降量及变化幅度，因此可令目标泛函为：

若存在多个控制点，则可将目标泛函设为：

通过求解式⒀～⒃所表示的最优控制问题，即可进行盾构掘进参数的优化，实现降低掘进导致地表沉降的目标。最优控制问题的解法包括解析法和数值法两种，解析法往往仅适用于部分形式简单的问题，大部分问题仍需通过数值法求解。数值法又可分为直接法和间接法两种，具体可参考文献[14]。

3 工程应用

某地铁盾构区间，隧道下穿既有铁路（见图2），双线铁路间距5.6 m。左线隧道拱顶埋深9.4 m，隧道直径6.0 m，盾构机外径6.3 m。为控制隧道掘进时对铁路造成的影响，隧道左线掘进时对掘进参数进行了优化，同时在铁路两侧分别设置沉降监测点。

图2 盾构隧道下穿既有铁路平面位置关系Fig.2 Plane Position Relationship of Existing Railway under Shield Tunnel

区间内主要地层自上而下包括：人工填土层、冲击-洪积层、残积土层、中风化灰岩带和微风化灰岩带等，如图3 所示。其中，人工填土层为素填土，质地松散、压缩性较好；冲积-洪积层以灰白、灰黄色中粗砂为主，呈中密状；残积土层主要由灰岩风化而成，呈软塑状，为高压缩性土，广泛分布于基岩顶面；中风化灰岩带裂隙发育，呈碎块状或块状，岩石基本等级为Ⅳ级；微风化灰岩带岩石较完整，岩质较坚硬，岩石基本等级为Ⅲ级。盾构穿越主要土层物理力学参数如表1所示。

图3 主要地层分布Fig.3 Main Strata Distribution

表1 主要土层物理力学参数Tab.1 Physical Mechanics Parameters of Major Soil Layers

以两个沉降监测点的中点为坐标原点，盾构掘进方向为轴正方向建立坐标系，取回归系数A=（0.01，5.1，-0.2826）、b=-58.4[13]，代入式⒀建立左线隧道掘进系统状态方程。

根据该地区相似盾构隧道的施工经验，选取掘进参数的合理范围为：

将式⒅代入式⒁即可得到控制变量的取值范围。

取3 倍盾构直径内的区域为盾构掘进的扰动范围[15]，取整后约为20 m，则初始条件和终端条件可分别设为x（t0）=-20 m 和x（t1）=20 m。

两个监测点的坐标分别为（-3.5，0，0）和（3.5，0，0），将该坐标代入式⒄，可得到优化问题的目标泛函。

利用梯度法[14]对上述最优控制问题进行数值求解，得到了优化后的掘进参数。为检查优化效果，在盾构远离既有铁路约60 m 后，选择了一段地质条件较为接近、地表较为开阔、长40 m 的区间，取其中点进行沉降对比。下穿既有铁路区间采用优化后的掘进参数，对比区间则未采用最优控制理论进行优化，两个区间的掘进参数如图4 所示。

根据优化结果，当盾构掘进至距离铁路约10 m时，应降低千斤顶推力和刀盘转速，以降低对围岩的扰动，同时适当加大土舱压力，增加对掌子面的岩土体的支撑。

在盾构下穿既有铁路区间和对比区间测得的地表沉降如图5所示，由监测结果可知，无论在盾构到达前或盾构远离过程中，经过掘进参数优化后，盾构掘进造成的地表隆起和沉降的幅度均有明显降低。

图4 盾构隧道下穿既有铁路掘进参数Fig.4 Shield Tunnel under the Existing Railway Tunneling Parameters

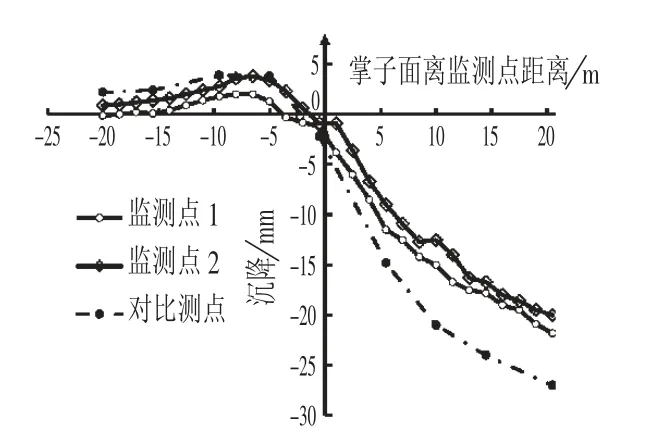
图5 各监测点沉降对比Fig.5 Comparison of Settlement at Monitoring Points

4 结论

在分析盾构隧道掘进造成地表沉降的基础上，结合最优控制理论，对掘进过程中的千斤顶推力、刀盘转速和土舱压力等参数进行了优化，并将该优化方法在工程中进行了应用，得到以下结论：

⑴盾构掘进过程中造成地表沉降的因素主要包括正面附加推力、刀盘摩擦、盾壳摩擦和盾尾间隙等，总沉降由各因素造成的沉降叠加而成；

⑵以千斤顶推力、刀盘转速和土舱压力为控制变量，以地表沉降为衡量优化效果的指标，可建立盾构掘进的最优控制问题，进行掘进参数的优化。

⑶工程应用结果表明，采用优化后的掘进参数，能有效降低掘进时造成的地表沉降，证明了该优化方法的适用性。