减震榫与榫形防落梁装置应用于高速铁路简支梁桥的简化计算方法

周友权,李承根

(中铁第一勘察设计院集团有限公司桥隧处,西安 710043)

1 概述

我国高速铁路桥梁中，应用最为广泛的是跨度32 m简支箱梁。据统计，京沪高铁跨度32 m双线简支梁占其桥梁总里程的90%以上[1]。目前，铁路桥梁抗震设计中，常用的减隔震装置有液体粘滞阻尼器、摩擦摆支座、铅芯橡胶支座[2-9]，均可发挥良好的减隔震作用，但是由于造价高，一般仅用于地震烈度高的特殊桥梁抗震设计。因此，针对应用最为广泛的铁路简支箱梁，结合铁路桥梁的抗震设防特点，研发了减震榫[10-18]与榫形防落梁装置。这两种装置构造简单、施工方便、性能可靠、价格低廉，其中榫形防落梁装置仅适用于地震动峰值加速度≤0.2g的地区，减震榫还适用于地震动峰值加速度>0.2g的地区。

为了使减震榫与榫形防落梁装置的使用、制造、安装规范化，有利于在铁路桥梁减隔震中的推广使用，中国铁路总公司组织了《铁路桥梁减震榫》技术标准的编制。本文给出了技术标准中装置应用于铁路简支梁桥抗震设计的简化计算方法与计算实例，可为工程技术人员采用该装置进行简支梁桥的抗震设计提供参考。

2 装置构造

减震榫主要由上榫体、下榫体、传力筒、连接夹板和预埋件等组成，结构示意如图1所示。

图1 减震榫结构示意

榫形防落梁装置主要由限位钢榫、承压环、限位环、预埋钢筒和橡胶密封圈等组成，按构造形式可分为整体式与分离式两类：整体式的限位钢榫由单根变截面钢榫组成，适用于现浇箱梁；分离式的限位钢榫由上、下两根变截面钢榫组成，两者通过偏心法兰连接，一般适用于整孔预制架设箱梁，分离式的结构示意如图2所示。

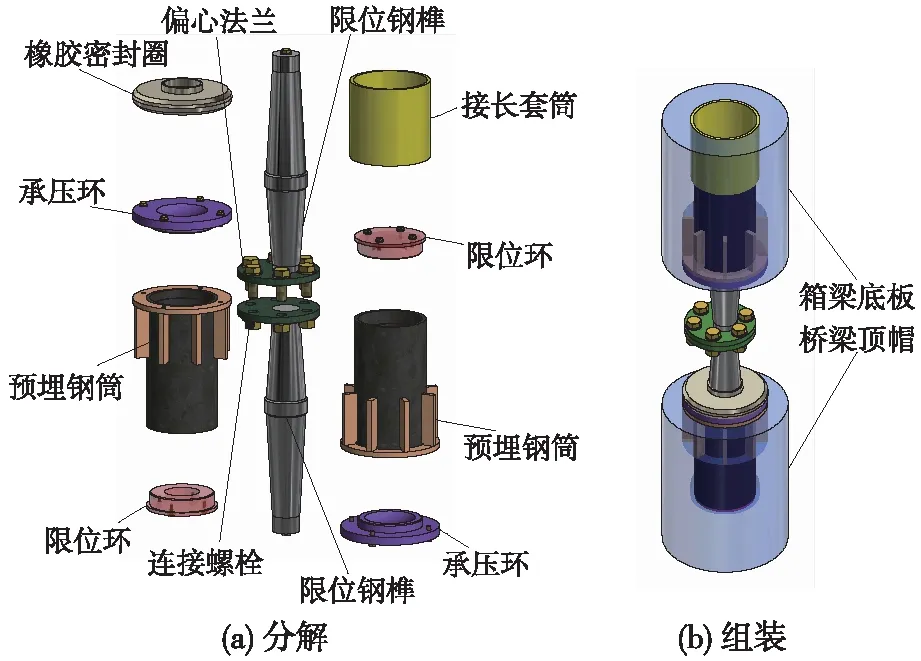
图2 分离式榫形防落梁装置结构示意

3 作用机理

减震榫是固结于箱梁梁端的梁底与墩顶之间，箱梁的原固定支座需改为活动支座，原活动支座不变。就受力行为而言，减震榫是由传力筒传递剪力的上下两个悬臂梁结构，属于弯剪构件，弹性状态下的受力变形行为如图3所示。

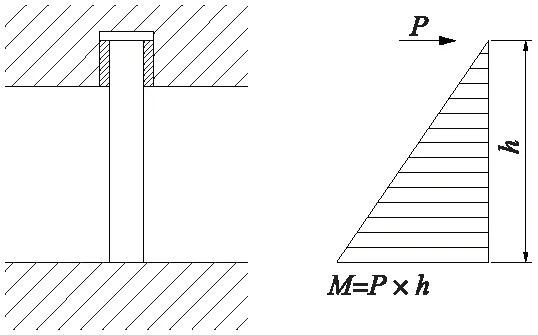
图3 减震榫受力变形示意

在正常使用状态下，梁体传来的竖向反力及梁端的转角仍由支座实现，但梁体的水平反力及水平位移则由减震榫支撑和控制，简支梁成为两端弹性约束的工作状态。地震发生后，梁体地震水平力将通过减震榫传至桥墩。通过对减震榫构造的精细化设计，在正常运营下满足列车对桥梁刚度的使用要求，在强震下能够产生足够的塑性变形，达到降低地震力的目的。

榫形防落梁装置设置于梁底与桥墩顶帽之间，在纵桥向与横桥向均预留一定的间隙，固定支座与活动支座附近均采用相同的装置。正常运营时，装置的状态如图4所示。

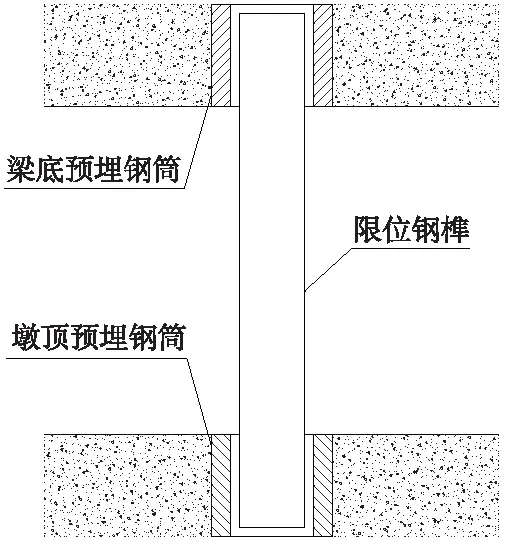
图4 榫形防落梁装置未发挥作用状态

由于榫形防落梁装置在纵向桥有预留间隙，温度作用下装置不受力，即装置对结构上部无附加刚度。上部结构传来的制动力、伸缩力及多遇地震水平力等，均由固定支座承担。超过多遇地震时，固定支座的销轴剪断，固定支座转变为活动支座，榫形防落梁装置开始发挥作用。当梁体与墩身产生的水平相对位移超出预留间隙时，装置中的限位钢榫上下端与钢筒内壁接触，开始受力产生弹性变形，继而发生塑性变形消耗地震能量起到减震作用，此时装置的状态如图5所示。由于装置的水平刚度小，与桥墩的合成刚度远小于原桥墩刚度，可延长结构周期起到隔震作用。榫形防落梁装置地震下产生的水平抗力，实现了有缓冲效应的限位效果，可以起到防落梁的功能。

图5 榫形防落梁装置发挥作用时状态

4 力学特性

为了解减震榫与榫形防落梁装置的弹塑性力学特征，在北京交通大学结构实验室进行了1∶1的模型试验，图6为减震榫典型的实测滞回曲线。

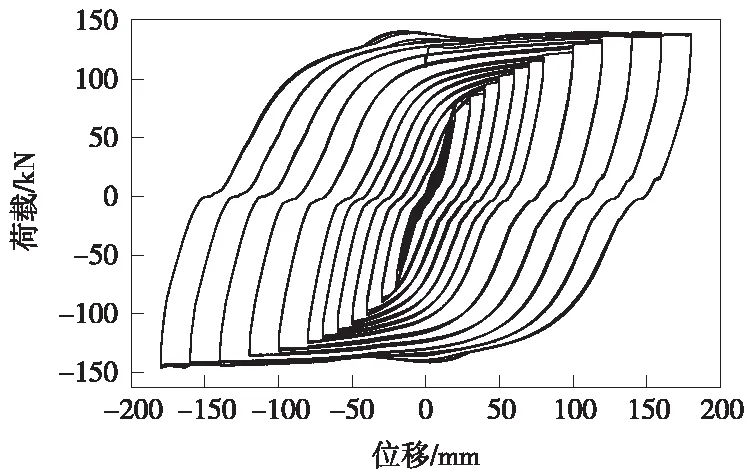
图6 减震榫模型试验滞回曲线

对减震榫滞回曲线中每一个位移对应的阻尼力与阻尼比进行提取分析，发现可以采用分段函数形式来拟合他们之间的关系。将减震榫的滞回曲线拟合后的水平承载力与水平位移、阻尼比与水平位移之间的关系曲线如图7、图8所示。

图7 减震榫位移与水平承载力关系曲线

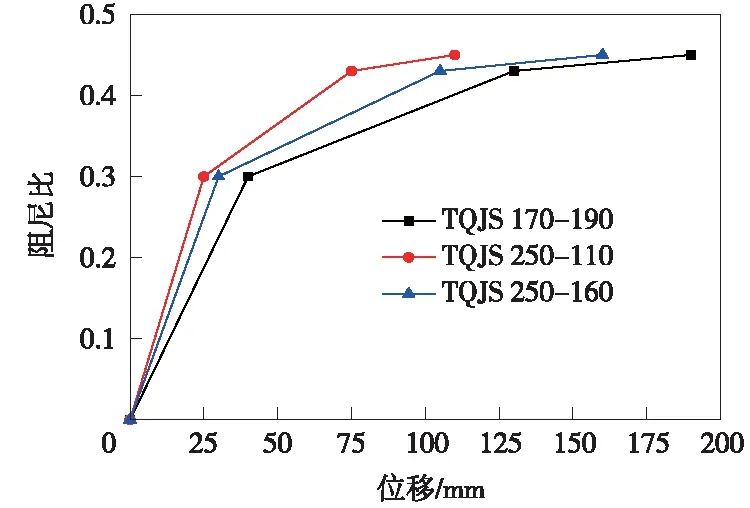
图8 减震榫位移与阻尼比关系曲线

榫形防落梁装置的实测滞回曲线如图9所示。

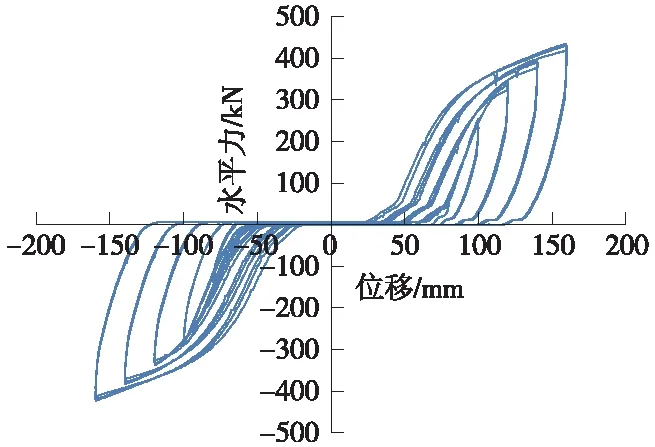
图9 榫形防落梁装置模型试验滞回曲线

榫形防落梁装置的滞回曲线拟合后的水平承载力与水平位移、阻尼比与水平位移之间的关系曲线如图10、图11所示。

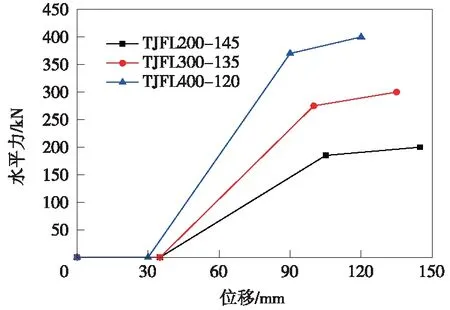
图10 榫形防落梁装置位移与水平输出力关系曲线

图11 榫形防落梁装置位移与阻尼比关系曲线

5 非线性反应谱法

在结构地震响应分析方法中，非线性时程分析方法是模拟地震时结构的性能较为理想和准确的方法，但该方法计算过程复杂，特别是对计算软件选择、计算模型的简化、钢筋混凝土本构关系的确定、非线性滞回模型的选取等问题，涉及到较专业的理论水平和经验知识。因此，除了特别复杂的结构设计和理论研究，该方法并不适用于在一般桥梁工程的减隔震设计中推广应用。

反应谱的概念在20世纪40年代由M Biot首次提出，尽管反应谱理论存在一定的局限性，但它从形式上将结构的动力设计简化为静力设计，具有概念清晰、计算简便、易于掌握等突出的优点。规范给出的设计反应谱是在大量地震记录基础上统计分析得到的地震响应曲线，能够真实反映结构在地震作用下受力变形的一般规律，具有很强的实用性，而且计算精度较高，可以满足桥梁设计的需求，非常适用于结构简单、刚度较大的铁路桥梁的地震分析。所以，反应谱方法得到了世界各国工程界的认同和推广应用。

按照铁路抗震规范[19]采用反应谱方法进行计算时，混凝土结构的阻尼比一般取0.05。但采用减震榫或榫形防落梁装置后，结构的阻尼比会大大提高，而阻尼是可以消耗地震能量的，由于阻尼的增大，结构的动力放大系数会下降，地震反应会减小。为考虑减隔震装置附加阻尼的影响，采用反应谱计算时引入了阻尼调整系数这一参数，即为非线性反应谱计算法。因此，减震榫或榫形防落梁进行减隔震设计时，推荐采用非线性反应谱法，以便于工程技术人员的应用。

6 简化计算方法

铁路简支梁桥由于结构质量大部分集中于上部的梁体，可采用单墩力学模型进行分析计算，分析统计发现，对于常规铁路简支梁桥的桥墩，计算中可忽略桥墩质量对桥墩周期的贡献。多遇地震时，装置不发挥作用或发挥很少作用，可按照规范[19]进行地震检算。超过多遇地震，对于采用榫形防落梁装置的桥梁，固定支座的销轴剪断成为活动支座，装置开始发挥作用；对于采用减震榫的桥梁，榫体将进入塑性耗能状态。对单墩模型计算地震作用时，可只计算基阶模态反应。利用计算的墩顶水平力进行墩身基础检算时，尚应考虑墩身质量的影响因素。由于减震榫与榫形防落梁的减隔震作用机理相同，二者应用于桥梁减隔震设计的简化计算方法完全一致。以榫形防落梁装置为例，介绍简化计算流程与相应公式。

假定榫形防落梁装置地震下的位移值为Δ，查图10与图11曲线对应位移下装置输出的水平力Fj与阻尼比ξj，则地震下墩顶对应水平合力为

P0=m·Fj+μ·M

(1)

式中m——单孔梁装置的个数；

μ——支座的水平摩阻系数，取0.03；

M——含二期恒载的梁部重力。

桥墩墩顶榫形防落梁装置在考虑支座摩阻力影响后的等量有效刚度Keff及等量阻尼比ξh分别为

(2)

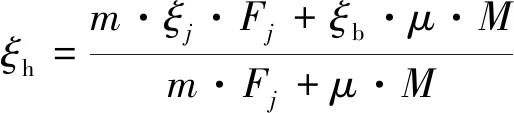
(3)

式中ξb——支座摩阻力滞回环对应阻尼比，取2/π。

桥墩抗剪刚度Ki与墩顶防落梁装置的等量有效刚度Keff串联后的桥墩合成刚度

(4)

则桥墩结构的一阶自振周期Te与动力放大系数β(0.45≤β≤2.25)分别为

(5)

(6)

式中Tg——场地特征周期。

桥墩墩顶榫形防落梁装置与桥墩合成阻尼比

(7)

式中ξp——桥墩阻尼比，可取0.05。

根据规范[19]阻尼调整系数

(8)

当η≤0.55时，取η=0.55

墩顶地震水平力

F0=α·β·η·M

(9)

式中α——地震动峰值加速度。

F0与P0有差别时，调整假定的位移值Δ，重复上述的计算过程，直至墩顶地震水平力F0与P0之间的相对误差小于1%，即可认为得到满足设计要求的墩顶地震水平力。通过上述计算过程，可对箱梁所采用的装置型号进行选取。

计算墩底地震力时，需要考虑桥墩质量的影响因素。地震下桥墩自身的阻尼比可取0.05，不用进行阻尼调整，则墩身质量M1在地震下的水平力F1计算公式为

F1=α·β·M1

(10)

墩底的地震水平力F与弯矩Mh的计算公式分别为

F=F0+F1

(11)

Mh=F0·H+F1·h

(12)

式中H——桥墩高度；

h——桥墩质心到墩底的距离。

得到墩底地震下的水平力与弯矩后，可进行桥墩检算与基础的配置。

7 计算实例

以某高速铁路32 m简支双线箱梁为计算实例，梁部与二期的恒载重力和为13 105 kN，桥墩高度为13 m、直坡，桥墩重力为3 800 kN，其顺桥向刚度Ki为500 kN/cm，设计地震动峰值加速度0.2g，特征周期0.45 s，采用榫形防落梁装置进行结构罕遇地震下的抗震设计。罕遇地震下，对应的地震动峰值加速度为0.38g，参考建筑抗震设计规范[20]特征周期增加0.05 s取0.5 s。每孔箱梁设置4根TJFL 400-120型榫形防落梁装置，单根防落梁的水平承载力400 kN，设计位移120 mm。假定地震下装置的位移为100 mm，根据图10、图11可得100 mm位移下装置对应的输出水平力Fj为380 kN，对应输出的阻尼比ξj为0.173，考虑支座摩阻力，则地震下墩顶对应水平合力为

P0=(4×380+0.03×13 105) kN=1 913 kN

桥墩墩顶装置考虑支座摩阻力影响后的等量有效刚度

Keff=1 913/10=191.3 kN/cm

桥墩墩顶装置考虑支座摩阻力影响后的等效阻尼比

0.268

桥墩合成刚度

桥墩结构的一阶自振周期

动力放大系数

桥墩墩顶防落梁装置与桥墩合成阻尼比

阻尼调整系数

墩顶地震水平力计算值

F0=0.38×0.582×0.649×13 105 kN=1 881 kN

P0>F0，说明装置假定的输出水平力偏大，需减小装置的假定位移，重复上面的计算过程。当装置的水平位移为97 mm时，F0计算值与P0基本一致。此时，墩顶地震水平力计算值F0为1 902 kN，动力放大系数为0.587。桥墩质心到墩底的距离可近似取墩高13 m的一半，则墩身顺桥向的水平地震力为

F1=0.38×0.587×3 800 kN=848 kN

墩底顺桥向的地震水平力

Fh=(1 902+848)kN=2 750 kN

地震产生的墩底顺桥向弯矩

Mh=(1 902×13+848×13/2) kN·m=

30 238 kN·m

减震榫用于简支梁桥的抗震计算过程与榫形防落梁的相同，计算时需注意选取减震榫位移下对应的阻尼力与阻尼比。

8 计算程序

由于上述计算过程需要进行多次迭代计算，为了方便设计人员采用减震榫与榫形防落梁进行铁路简支梁的抗震设计，根据上面介绍的非线性反应谱分析方法及步骤，编写了“铁路简支梁桥抗震用减震榫分析程序”，程序界面如图12所示。

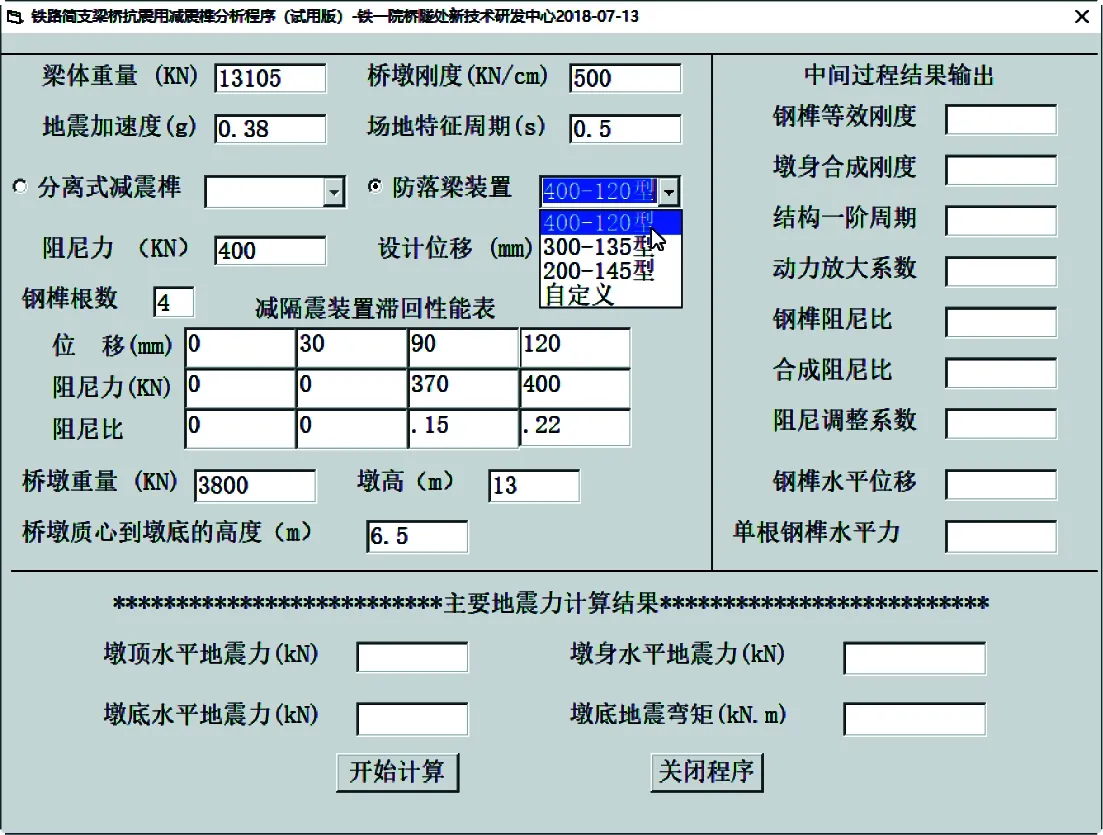
图12 计算程序输入界面

使用时，设计者首先应输入地震加速度、场地特征周期、梁体重力，以及桥墩刚度、重力、高度、桥墩质心到墩底高度这些基本信息，然后选择减隔震装置的类型及型号，选定后该型号的滞回性能将自动填入，当程序内提供的型号不满足要求时，设计者可选择自定义模式，人工填写通过试验得到的减隔震装置的滞回性能，最后，选定每孔梁需要布置的减隔震装置的数量。数据输入如图12所示，参数输入完毕后，按下开始计算键，程序进行计算。计算输出界面见图13。

图13 计算程序输出界面

图13给出了上节工程实例的程序计算结果，程序右侧为中间计算过程的数据输出，给出了钢榫等效刚度(含支座摩阻力影响)、墩身合成刚度、结构一阶周期、动力放大系数、钢榫阻尼比(含支座摩阻力影响)、合成阻尼比、阻尼调整系数等中间计算成果，供设计者使用。用于桥墩检算与墩底基础设置的计算结果为地震下墩底的水平力与弯矩。

设计者应注意核查钢榫水平位移，当钢榫水平位移不超过减隔震装置的设计位移时，表明减隔震装置的选型是可行的。当钢榫水平位移超限时，应改变装置的类型或型号，或调整每孔梁上装置的布置数量，重新进行计算，直至满足要求。

9 结语

减震榫与榫形防落梁装置，为新研发的适用于铁路简支梁的减隔震产品，装置在地震下发挥作用时表现为非线性特性，为避免复杂的非线性计算分析，降低计算难度，采用非线性反应谱法，给出了减震榫与榫形防落梁应用于铁路简支梁桥的简化计算方法与计算实例，并给出了对应的分析计算软件及其使用方法，以便于工程技术人员的应用。