A Remark on Double Ore Extensions
(School Of Mathematical Sciences,ZheJiang University,Hangzhou 310027,China)
Abstract:The aim of this article is to summarize the relationship between double Ore extensions and iterated Ore extensions,and mainly describe the lifting of properties from an algebra A to a(right)double Ore extension B of A which can not be presented as iterated Ore extensions.
Key words:double Ore extension;iterated Ore extension;lifting of properties
§1. Introduction
In 2008,James J.Zhang and Jun Zhang introduced a new construction for extending a given algebra A,called a double Ore extension,this constriction resembles that of an Ore extension.In 2011,Paula A.A.B.Carvalho,Samuel A.Lopes and Jerzy Matczuk described the common part of the Ore extension and double Ore extension of A and o ff ered necessary and sufficient conditions for a double Ore extension AP[y1,y2;σ,δ,τ]to be presented as iterated Ore extensions of the form A[y1;σ1,δ1][y2;σ2,δ2]or A[y2;σ2,δ2][y1;σ1,δ1].They also revealed that the ring-theoretical properties can be lifted from A to a(right)double Ore extension B of A in the iterated case.However,it should be noted that there are no inclusions about the lifting of ring-theoretical properties from A to a(right)double Ore extension B of A in the double case.
The aim of this article is to summarize the relationship between double Ore extensions and iterated Ore extensions,and mainly describe the lifting of properties from an algebra A to a(right)double Ore extension B of A which can not be presented as iterated Ore extensions.We also give partial answers to the last four questions posed in[4].
In Section 1,we parallel the constructions of double Ore extensions and Ore extensions,giving some proofs which were omited in[2]and introduce the necessary and sufficient conditions which were mentioned.In Section 2,we give specific examples of ring-theoretical properties which can be lifted from A to a(right)double Ore extension B of A in the iterated case.In Section 3,we investigate the lifting of properties given in Section 2 from A to a(right)double Ore extension B of A in the double case.
Throughout this article,k is a field and k∗is its multiplicative group of units.Everything is over k.
§2. Double Ore Extensions Versus Iterated Ore Extensions
In this section,we give definitions and summarize the relationship between double ore extensions and iterated ore extensions,some proofs are supplied if they were omitted in corresponding references.
Definition 2.1 Let α be an endomorphism of an algebra A and δ an endomorphism of the additive group(A,+).Then δ is called an α derivation of A if δ(ab)= α(a)δ(b)+ δ(a)b for all a,b in A.Note in particular that σ(1)=1 and δ(1)=0.
Definition 2.2 The Ore extension A[x;σ,δ]of an algebra A is a noncommutative algebra obtained by giving the algebra of polynomials A[x]a new multiplication,subject to the identity xa= σ(a)x+ δ(a).
Remark 2.1 The noncommutative algebra A[x;σ,δ]is also called skew polynomial algebra.If δ=0,it is denoted by A[x;σ]and is called asymmetric polynomial algebra,if σ =1,it is denoted by A[x;δ]and is called di ff erential polynomial algebra.
Lemma 2.1 The following statements about an Ore extension A[x;σ,δ]are equivalent:
(1)Ore extension A[x;σ,δ]is a free right A-module with basis
(2)σ is an automorphism of A;
(3)σ is injective and xA+A=Ax+A.
Proof (1) ⇒ (2)If a ∈ kerσ,then σ(a)=0,xa= δ(a),since A[x;σ,δ]is a free right A-module,hence a=0,σ is injective.It is clear that A[x;σ,δ]is a free left A-module,notice that for an arbitrary a ∈ A,there exists a0∈ A,ax=xa0= σ(a0)x,hence σ is surjective.Thus,σ is an automorphism.
(2)⇒ (3)Obviously σ is injective,the condition xa= σ(a)x+δ(a)implies xA+A ⊆ Ax+A.For arbitrary a1,a2∈ R,a1x+a2∈ Ax+A,since σ is surjective,there exists∈ A,a1= σ(),thus= σ()x+ δ()=a1x+ δ(),hence a1x+a2=− δ()+a2∈ xA+A,Ax+A⊆xA+A,so xA+A=Ax+A.
(3)⇒ (1)For each f(x)∈ A[x;σ,δ],fthe condition xA+A=Ax+A implies thatIfthen ai=0,notice that the coefficient of xiis also σi(),since σ is injective,thus=0,so A[x;σ,δ]is a free right A-module.
The definition of the double Ore extension is based on the Ore extension.
Definition 2.3 Let A be an algebra and B be another algebra containing A as a subalgebra.We say B is a right double Ore extension of A if the following conditions hold:
(1)B is generated by A and two new variables y1and y2;
(2){y1,y2}satisfies a relation

where p12,p11∈ k and τ1,τ2,τ0∈ A;
(4)y1A+y2A+A⊆Ay1+Ay2+A.
Let P denote the set of scalar parameters{p12,p11}and let τ denote the set{τ1,τ2,τ0}.We call P the parameter and τ the tail.Similarly,we can define the left double Ore extension B of A.We say B is a double Ore extension if it is a left and right double Ore extension of A with the same generating set{y1,y2}.
Remark 2.2 Condition(4)in Definition 1.3 from the above definition is equivalent to the existence of two maps
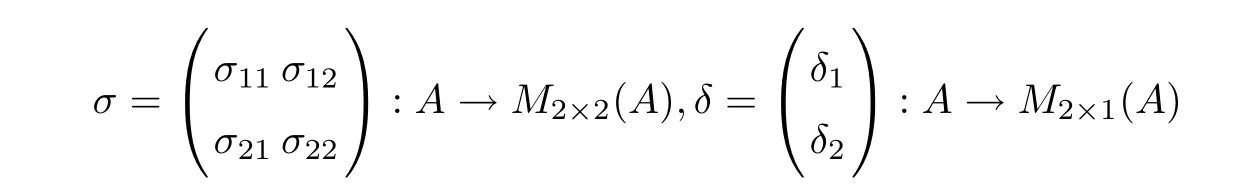
Proof Consider the necessity.If y1A+y2A+A⊆Ay1+Ay2+A,then∀a∈A,∃map σ11,σ12,σ21,σ22,δ1,δ2:A → A,subject to
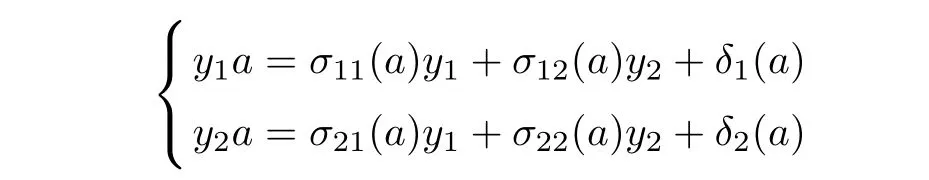
It implies the existence of two maps
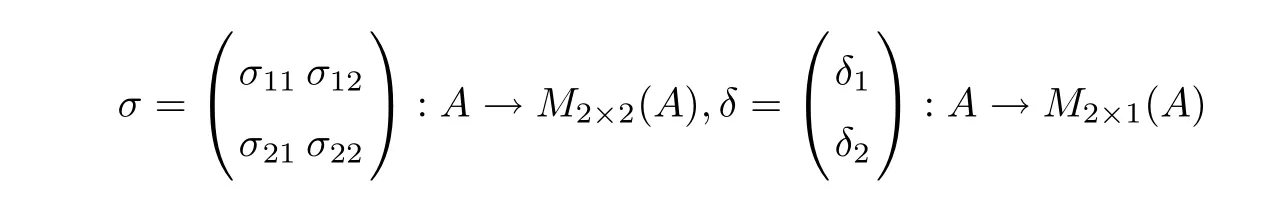
which satisfies

for all a∈A.The sufficiency is obvious.
Let B be a right double Ore extension of A,we denote B=AP[y1,y2;σ,δ,τ],where P={p12,p11} ⊆ k,τ={τ1,τ2,τ0} ⊆ A,and σ,δ are as above.
Example 1.1 A trivial example of a right double Ore extension is when A=k.A right double Ore extension of k,denoted by B,is isomorphic toas a k-vector space.It is isomorphic to the algebra khy1,y2i/(r),where r is the relation

for some p12,p11,a1,a2,a3∈k.
In[1],by choosing a suitable basis of the vector space ky1+ky2,we can prove the following lemma.
Lemma 2.2[1,Lemma1.7]Let B=AP[y1,y2;σ,δ,τ]be a right double Ore extension.
(1)If p116=0 and p12=1,thenwhere

(2)If p126=1,thenwhere

Proof (1)Let B=A{p12,0}[y1,y2;σ,δ,τ]be a double ore extension,then B has a naturalfiltration,given by setting degA=0 and degy1=degy2=1.As an associated graded algebra,
(2)Let B0=A,B1=A+Ay1+Ay2,B2=A+Ay1+Ay2++Ay1y2+,···,then{0} ⊂ B0⊂ B1⊂ ···⊂ Bi⊂ ···⊂ B satisfiesBiand for all m,n∈ N,Bm·Bn⊂Bn+m.Hence,B is a filtrated algebra,we can get a associated graded algebra grB=Gn,where G0=B0and for all n>0,Gn=Bn/Bn−1,the multiplication is defined by(x+Bn−1)(y+Bm−1)=xy+Bn+m−1for all x∈Bnand y∈ Bm.
Let y1,y2∈B1,z1=y1+A=∈B1/B0,z2=y2+A=∈B1/B0,then G1is generated by A and z1,z2,since z1z2==,then Gncan be generated by A and z1,z2,hence,grB can be generated by A and z1,z2.Furthermore
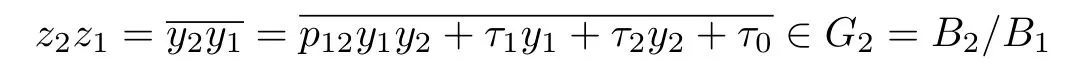
so τ1= τ2= τ0and
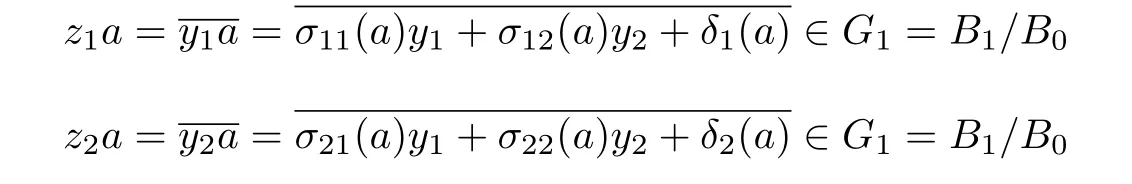
Hence,δ1(a)= δ2(a)=0,then grBAP0,{0,0,0}].
Corollary 2.1 Suppose that B=AP[y1,y2;σ,δ,τ]is a right double Ore extension of A with p126=1.Then,there exists a filtration on B such that the associated grated algebra D=grB can be presented as follows:
(1)D is generated over A by indeterminates z1,z2;
(2)D is free as a left A-module with basis{:i,j≥0};
(3)Multiplication in D is given by multiplication in A and the conditions z2z1=p12z1z2and z1A+z2A⊂Az1+Az2with za=,where z=(z1,z2)0,is obtained from σ andas in Lemma 1.3(b).
Furthermore,suppose B is a double Ore extension of A,then D is also free as a right A-module with basis{:i,j≥0}and z1A+z2A+Az1+Az2.
In[1],the authors have given necessary and sufficient conditions for a double Ore extension B=AP[y1,y2;σ,δ,τ]to be presented as iterated Ore extensions of the form A[y1;σ1,d1][y2;σ2,δ2]or A[y2;σ2,δ2][y1;σ1,δ1].
Theorem 2.1[1,Theorem2.2]Let A,B be k-algebras such that B is an extension of A.Assume P={p12,p11} ⊆ k,τ={τ1,τ2,τ0} ⊆ A,σ is an algebra homomorphism from A to M2×2(A)and δ is a σ-derivation from A to M2×1(A).
(1)The following conditions are equivalent:
(a)B=AP[y1,y2;σ,δ,τ]is a right double Ore extension of A which can be presented as an iterated Ore extenision A[y1;σ1,d1][y2;σ2,d2];
(b)B=AP[y1,y2;σ,δ,τ]is a right double Ore extension of A with σ12=0;
(c)B=A[y1;σ1,d1][y2;σ2,d2]is an iterated Ore extension such that

for some pij∈ k,τi∈ A.The maps σ,δ,σiand δi,i=1,2 are related by
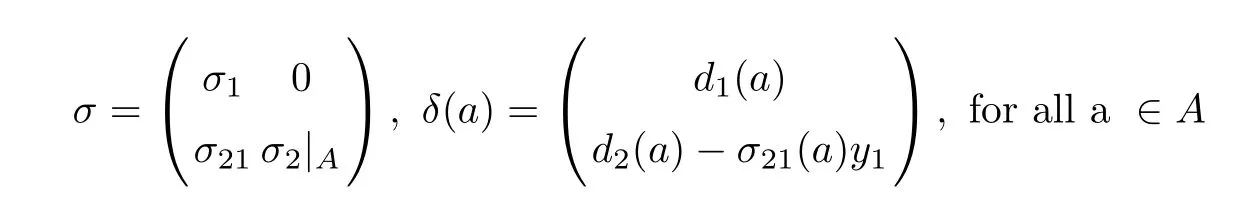
(2)If one of the equivalent statements from(1)holds,then B is a double Ore extension of A if and only if σ1= σ11and σ2|A= σ22are automorphism of A and p126=0.
Theorem 2.2[1,Theorem2.4]Let B=AP[y1,y2;σ,δ,τ]be a right double Ore extension of the k-algebra A,where P={p12,p11} ⊆ k,τ={τ1,τ2,τ0} ⊆ A,σ :A → M2×2(A)is an algebra homomorphism and δ:A → M2×1(A)is a σ-derivation.Then B can be presented as an iterated Ore extension A[y2;][y1;]if and only if σ21=0,p126=0 and p11=0.In this case,B is a double Ore extension if and only if= σ22and= σ11are automorphisms of A.
Remark 2.3 Theorem 1.1 and Theorem 1.2 shows the necessary and sufficient conditions for a double Ore extension B to be presented as iterated Ore extensions of A,which gives a method to lift the ring-theoretical properties(being a domain,being prime(semiprime),being right noetherian,having finite right Krull dimension,having finite global dimension)from A to a(right)double Ore extension B of A which can be presented as iterated Ore extensions.We will illustrate the details in Section 2.
§3. Iterated Ore Extension and Its Properties
In this section,we give specific examples of ring-theoretical properties which can be lifted from A to a(right)double Ore extension B of A in the iterated case.First,we show the properties of A are,of course,reflected in those of A[x;σ,δ].Some proofs are omited if they were given in[2].
Theorem 2.1[2,Theorem1.2.9]Let S=A[x;σ,δ],then
(1)If σ is injective and A is a domain,then S is a domain.
(2)If σ is an automorphism and A is a prime(semiprime)ring,then S is a prime(semiprime)ring.
(3)If σ is an automorphism and A is left(right)noetherian,then S is left(right)noetherian.
Definition 3.1 If a,b belongs to a poset A,and a≥b,then we define a/b={x∈A|a≥x≥b}.This is a subposet of A and is called the factor of a by b.By a descending chain{an}of elements of A is meant that a1≥ a2≥ ···an≥ ···;and the factors ai/ai+1are called the factors of the chain.The poset A is said to satisfy the d.c.c(or to be an antichain)provided that every descending chain in A is eventually constant.
Definition 3.2 We now define the deviation of a poset A,devA for short.If A is trival then devA=−∞.If A is nontrival but satisfies the d.c.c.then devA=0.For a general ordinal α,we define devA= α provided:
(1)devA 6=β<α;
(2)In any descending chain of elements of A all but finitely many factors have deviation less than α.
Proposition 3.1[2,Proposition6.2.1]Let f:A → B be a poset map,and let γ,δ be ordinals with γ+δ≤ δ+ γ.Suppose that whenever dev(a1/a2)≥ δ for ai∈ A,then dev(f((a1)/f(a2))≥ γ.
(1)If either there is no factor(a1/a2)in A with dev(a1/a2)≥ δ or there is no factor b1/b2in B with devb1/b2≥ γ,then devA ≤ δ;
(2)Otherwise γ +devA ≤ δ+devB.
Definition 3.3 If M is a right R-module then the Krull dimension of M,written K(M),is defined to be the deviation of L(M),the lattice of submodules of M.In particular,K(RR)is the right Krull dimension of R.
Lemma 3.1[2,Proposition6.5.3]Let R⊆T be a ring extension,θ:L(RR)→L(TT)with A 7→ AT for A is a right ideal of R,which preserves proper containment,then K(RR)≤ K(TT).
Corollary 3.1[2,Corollary6.5.3]Let R⊆T be a ring extension such thatRT is free,then K(RR)≤K(TT).
Proof SinceRT is free,so it is flat,then AT ∼=A ⊗ T,θ preserves proper containment,by Lemma 2.1,K(RR)≤K(TT).
Theorem 3.2[2,Theorem6.5.4]Let R be a ring of finite right Krull dimension,σ an automorphism and δ a σ-derivation,then K(R) ≤ K(R[x;σ,δ]) ≤ K(R)+1;In particular,if δ=0,then K(R[x;σ])=K(R)+1.
Definition 3.1 One defines the projective dimension of a right R-module MR,written pdMR,to be the shortest length n of a projective resolution.

or∞if no finite projective resolution exists.
Definition 3.5 The right global dimension of a ring R,denoted by rgldR,is defined to be the super bound of pdMRfor all right R-modules M.
Theorem 3.3[2,Theorem7.5.3]Let R be a ring of finite global dimension,σ an automorphism and δ a σ-derivation,then rgldR ≤ rgld(R[x;σ,δ])≤ rgldR+1.
The next theorem is based on Theorem 1.1 and the ring-theoretical properties of an Ore extension mentioned in the section.
Theorem 3.4 Suppose B=AP[y1,y2;σ,δ,τ]is a double Ore extension of A which can be presented as an iterated Ore extenision A[y1;σ1,d1][y2;σ2,d2].
(1)If σ1= σ11and σ2|A= σ22are injective and A is a domain,then B is a domain.
(2)If A is a prime(semiprime)ring,then B is a prime(semiprime)ring;
(3)If A is left(right)noetherian,then B is is left(right)noetherian;
(4)If A is a ring of finite right Krull dimension,then K(A)≤K(B)≤K(A)+2;In particular,if δ=0,then K(B)=K(A)+2;
(5)If A is a ring of finite global dimension,then rgldA≤rgldB≤rgldA+2.
Remark 3.1 Theorem 2.4 illustrates the details of lifting.However,the aim of this paper is to show that the lifting need not to be depended on iterated Ore extensions,some examples are given in Section 3 to illustrate the idea.
§4. Double Ore Extension and Its Properties
In this section,we investigate the lifting of properties given in Section 2 from A to a(right)double Ore extension B of A in the double case.Some proofs are omited if they were given in[2].
Theorem 4.1 Suppose B=AP[y1,y2;σ,δ,τ]is a right double Ore extension of A.kerσ12=kerσ21=k,p12=1 and A is a domain,then B is a domain.
Proof Consider the monomialsand,the product of the monomials is a mapping φ :B ×B → B,now we explain that φ is injective.Supposeandthey are polynomials of degree m and n respectively,and aij,bklare nonzero leading coefficients.We make a convention
(1)In the first position of the Cartesian product,if s1 (2)In the second position of the Cartesian product,if t1 In this sense,we get a unique monomial through φ.Then we multiply the monomials and get (1)If bkl∈ k,notice that σ11(k)= σ22(k)=k,σ12(k)= σ21(k)=0,p12=1,the leading term of fg is Since kerσ11=kerσ22=,then the leading coefficients is nonzero,so the degree of fg is n+m.Hence B is a domain. (2)If bkl∈,notice that σ11=σ22=0,p12=1,the leading term of fg is Since kerσ12=kerσ21=k,then the leading coefficients is nonzero,so the degree of fg is n+m.Hence B is a domain. (3)If bkl∈A,without loss of generality,suppose bkl=,where∈k,notice that σ11=σ22=0,p12=1,the leading term of fg is Since kerσ12=kerσ21=k,A=k ⊕,then the leading coefficients is nonzero,so the degree of fg is n+m.Hence B is a domain. Theorem 4.2 Suppose B=AP[y1,y2;σ,δ,τ]is a right double Ore extension of A.=kerσ21=k,p12=1 and A is a prime(semiprime)ring,then B is a prime(semiprime)ring. Proof The sorting for the elements in B is as in the Theorem 3.1.Suppose f and g are the given polynomials in the proof of Theorem 3.1,since,kerσ12=kerσ21=k,p12=1,each element of Equation 3.1,Equation 3.2 or Equation 3.3 in Theorem 3.1 is the leading coefficient of some element of fAg.Thusand so.Hence B is a prime(semiprime)ring. Lemma 4.1 If S is a filtered ring and grS is right noetherian then S is right noetherian. Lemma 4.2 if S is a filtered ring and I is the right ideal of S.The map I 7→grI is a partially ordered set map L(SS)→L(grSgrS)which is injective on chains. Lemma 4.3 Let R,S be rings with R⊂S,RS faithfully flat and rgldR<∞.If SRis projective,then rgldR≤rgldS. Lemma 4.4 Let S be a filtered ring,then rgldS≤rgldgrS. Theorem 4.3 Suppose A is a finitely generated commutative algebra,that is,for I is an ideal ofNowis a right double Ore extension of A.We denotethen (1)B is right noetherian; (2)B is a ring of finite right Krull dimension; (3)If B is a double Ore extension of A,then B is a ring of finite global dimension. Thus,grB is the iterated Ore extensionwhere σ0(z1)= (1)By Hilbert’s Basis Theorem,grB is right noetherian,then B is right noetherian. (2)On the one hand,notice thatAB is free,by Corollary 2.1,K(AA)≤K(BB);on the other hand,by Theorem 2.4,K(grB)=K(k[z1])+1+K(A)=K(A)+2,by Lemma 3.2 and Proposition 2.1,we have K(B)≤K(grB)=K(A)+2.To summarize,K(A)≤K(B)≤K(A)+2. (3)On the one hand,since B is a double Ore extension,henceAB and BAare free,soAB is faithfully flat and BAis projective,by Lemma 3.3,rgldA≤rgldB;on the other hand,by Theorem 2.4,rgld(grB)=rgld(k[z1])+1+rgld(A)=rgld(A)+2,by Lemma 3.4,we have rgld(B)≤rgld(grB)=rgld(A)+2.To summarize,rgld(A)≤rgld(B)≤rgld(A)+2. (1)B is right noetherian; (2)B is a ring of finite right Krull dimension; (3)If B is a double Ore extension of A,then B is a ring of finite global dimension. Proof Consider that when hji=1,then A=k[x1,x2,···,xn]is a special case of Theorem 3.3. Thus,grB is the iterated Ore extensionwhere σ0(z1)= The following proof is similar to Theorem 3.3.In particular,by Theorem 2.4,we have n≤K(B)≤n+2. Remark 4.1 Notice that in Theorem 3.1,Theorem 3.2,Theorem 3.3 and Theorem 3.4,B need not to be the iterated Ore extension of A,but we have lifted the properties given in Section 2 from A to a(right)double Ore extension B of A in these special cases. Lemma 4.5 Let B=kP[y1,y2;σ0,δ0,τ].Then Bk[x1][x2;σ2,d2]is an iterated Ore extension,where σ2is the algebra endomorphism of the polynomial ring k[x1]defined by σ2(x1)=p12x1+ τ2and d2is the σ2derivation of k[x1]given by d2(x1)=+τ0.Moreover,B is a double Ore extension of k if and only if In[3],Yongjun Xu,Hua-Lin Huang and Dingguo Wang generalized the Ore extension and double Ore extension and introduced the definition of multiple Ore extension. Definition 4.1 Let A be an algebra and B be another algebra containing A as a subalgebra.We say B is a n-Ore extension of A if the following conditions hold: (1)B is generated by A and n new variables y1,y2,···,yn; (2)For any 1 ≤ i (4)There exist a k-linear map σ :A → Mn(A)and a k-linear map δ:A → A⊕nsuch that where Mn(A)is the k×k matrix algebra with entries in A. Set then we denote the n-Ore extension B of A by B=A[y1,y2,···,yk;σ,δ,P,T].When k ≥ 2,the n-Ore extension is called a multiple Ore extension. Acknowledgements. The author thanks supervisor D.-M.Lu for useful conversations on the subject,for providing the references,for reading an earlier version of the paper and for his useful comments.

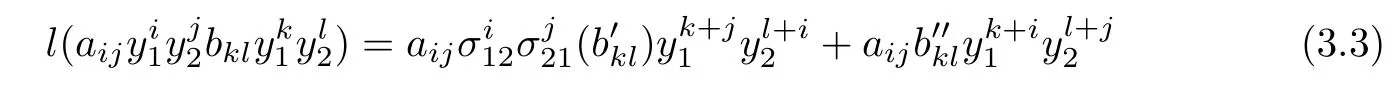
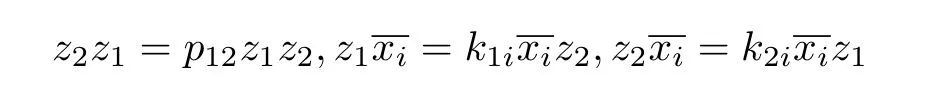
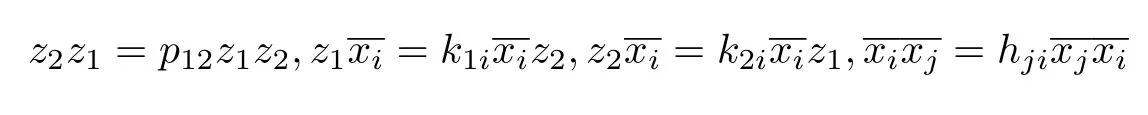

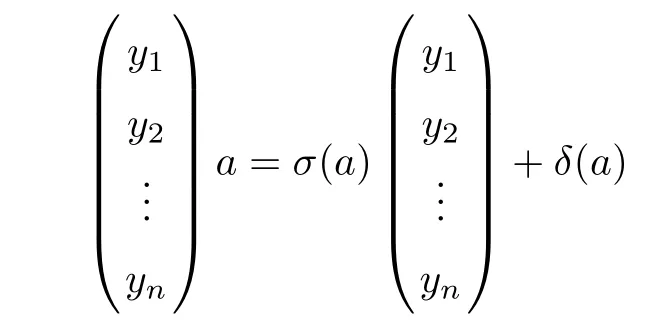
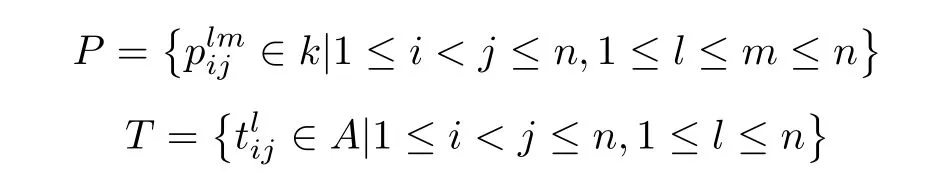
 Chinese Quarterly Journal of Mathematics2019年1期
Chinese Quarterly Journal of Mathematics2019年1期
