Some Results on H-cordial Graphs and Semi-H-cordial Graphs

CHEN Li-na,XIE Yan-tao

(1.Department of Mathematical Science of Yang-en University,Quanzhou 362014,China;2.Department of Management,Fujian Economy and Trade College,Quanzhou 362000,China)

Abstract:I.Cahit calls a graph H-cordial if it is possible to label the edges with the numbers from the set{1,−1}in such a way that,for some k,at each vertex v the sum of the labels on the edges incident with v is either k or−k and the inequalities|v(k)−v(−k)|≤ 1 and|e(1)−e(−1)|≤ 1 are also satisfied.A graph G is called to be semi-H-cordial,if there exists a labeling f,such that for each vertex v,|f(v)|≤ 1,and the inequalities|ef(1)−ef(−1)|≤ 1 and|vf(1)−vf(−1)|≤ 1 are also satisfied.An odd-degree(even-degree)graph is a graph that all of the vertex is odd(even)vertex.Three conclusions were proved:(1)An H-cordial graph G is either odd-degree graph or even-degree graph;(2)If G is an odd-degree graph,then G is H-cordial if and only if|E(G)|is even;(3)A graph G is semi-H-cordial if and only if|E(G)|is even and G has no Euler component with odd edges.

Key words:H-cordial;Odd-degree graph;Semi-H-cordial

§1. Introduction

We shall consider finite,undirected and simple graphs only.The reader is referred to[1]and[2]for undefined terms and concepts.

For a labeling of a graph G we mean a map f which assigns to each edge of G an element of{−1,1}.If a labeling f is given for a graph G without isolated vertex,for each vertex v of G we definewhere I(v)is the set of all edges incident to v.For an integer c we define to ef(c)be the number of edges having labeling c,and similarly vf(c)is the number of vertices having labeling c.M.Ghebleh and R.Khoeilar have proved the following lemma which states a simple but essential relation.

Lemma 1[3]If f is an assignment of integer number to the edges and vertices of a given graph G such that for each vertex v,then

I.Cahit has introduced the concept of H-cordial.

Definition 1[4]A labeling f of a graph G is called H-cordial,if these exists a positive constant k,such that for each vertex v,|f(v)|=k,and the following two conditions are satisfied:|ef(1)−ef(−1)|≤ 1 and|vf(k)−vf(−k)|≤ 1.A graph G is called to be H-cordial,if it admits a H-cordial labeling.

M.Ghebleh and R.Khoeilar have proved the following lemma.

Lemma 2[3]If a graph G with n vertices and m edges is H-cordial,then m−n is even.

I.Cahit proved that no H-cordial tree exists,then he introduced another concept of semi-H-cordial.

Definition 2[4]A labeling f of a tree T is called semi-H-cordial,if for each vertex v,|f(v)|≤ 1,and|ef(1)− ef(−1)|≤ 1 and|vf(1)− vf(−1)|≤ 1.A tree T is called to be semi-H-cordial,if it admits a semi-H-cordial labeling.

M.Ghebleh and R.Khoeilar gave a proof of the following theorem.

Theorem 1[3]A tree T is semi-H-cordial,if and only if it has an odd number of vertices.

Obviously,the definition of semi-H-cordial can generalized to each graph as following.

Definition 3 A labeling f of a graph G is called semi-H-cordial,if for each vertex v of G,|f(v)|≤ 1,and|ef(1)−ef(−1)|≤ 1 and|vf(1)−vf(−1)|≤ 1.A graph G is called to be semi-H-cordial,if it admits a semi-H-cordial labeling.

Lemma 3 If a graph G is semi-H-cordial,then|E(G)|is even.

Proof If a graph G is semi-H-cordial,then f(v)∈ {−1,0,1}.Note that

If|E(G)|is odd,then|ef(1)− ef(−1)|≥ 1.It implies that

It contradicts to the condition of Definition 3.

Example 1 C4is semi-H-cordial but is not H-cordial.

Example 2 K7is H-cordial.Since it has an odd number of edges,then it is not semi-H-cordial.

Definition 4 An odd-degree graph G is a graph that all of the vertex is odd vertex.

§2. Main Results

Theorem 2 An H-cordial graph G is either odd-degree graph or even-degree graph.

Proof Suppose that G has an odd vertex x and even vertex y.Then for each labeling f of G,we have f(x)is odd and f(y)is even.Hence there is not such a constant k in Definition 1.

We present the theorem in[1]as our lemma.

Lemma 4[1]For a connected nontrivial graph with exactly 2k odd vertices,the minimum number of trails that decompose it is max{k,1}.

Theorem 3 Let G be an odd-degree graph,then G is H-cordial if and only if|E(G)|is even.

Proof (Necessity)We know that the number of vertices of an odd-degree graph is even.By lemma 2,the necessity is obviously.

(Sufficiency)Assume that the components of G are G1,G2,···,Gn,then Gi(i=1,···,n)is an odd-degree graph.Suppose that

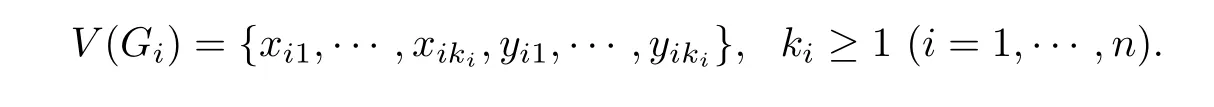
By lemma 4,we can decompose graph Giinto kitrails.Assume that the j-th trail of Giis Txijuij1uij2···uijrijyij(j=1,2,···,ki).Note that if a vertex w is internal vertex of any trail,then w has exactly even edges incident to it.However G is odd-degree graph,then each vertex of Gimust be an end-point of some trails.On the other hand,Gihas kitrails exactly,it implies that each vertex of Giis exactly an end-point of one trail.

We assign all the edges of G by the order of components and trails as following:

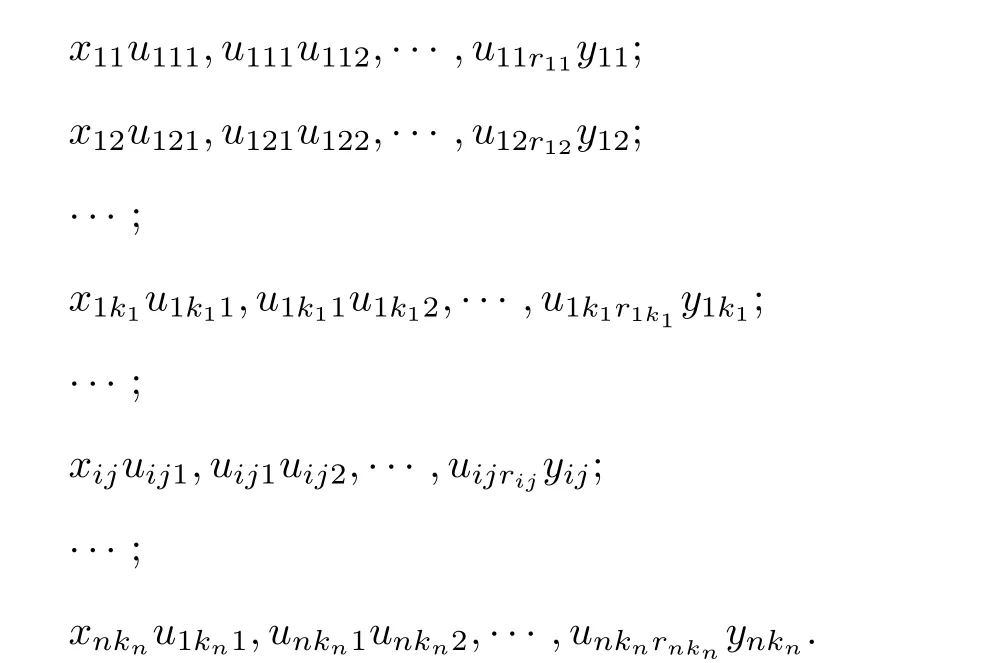
xijand yijare the two end-points of the j-th trail in Gi,uijtis the t-th internal vertex of thej-th trail of Gi.We give−1 and 1 alternatively to the above edges.It is easy to see that as an internal vertex gets labeling 0 and as an end-point gets labeling−1 or 1.Since each vertex v is the end-point of the trail once exactly.Hence f(v)∈ {−1,1},Since|E(G)|is even,we have ef(1)=ef(−1)and byWe know that vf(1)=vf(−1),so G is H-cordial.

Theorem 4 A graph G is semi-H-cordial if and only if|E(G)|is even and G has no Euler component with odd edges.

Proof (Necessity)By lemma 3,we know that|E(G)|is even.If G has a Euler component G∗and|E(G∗)|is odd,then

Since the degree of each vertex of Euler component G∗is even,then it is easily to see that there is at least one vertex v of G∗such that|f(v)|≥ 2.It contradicts to the condition of definition 3.

(Sufficiency)Assume that G1,···,Gn;Gn+1,···,Gmare the all components of G,and Gi(1≤i≤n)has odd vertex and Gj(n+1≤j≤m)has no odd vertex.Since Gj(n+1≤j≤m)is Euler component,so each Gjcontains an Euler tour,denoted by Ej.We give labeling −1 and 1 alternatively to Ej,Ej+1,···,Em.Since the number of the edges is even in Gj(n+1≤ j≤ m),we obtain that ef(−1)=ef(1)and f(v)=0 in Gj(n+1≤ j≤ m).Let xi1,···,xiki;yi1,···,yikiare all the odd-degree vertices of Gi(1 ≤ i≤ n).By lemma 4,Gican be decomposed into kitrails.Let the t-th trail of Gibe Txituit1uit2···uitrityit(1 ≤ i ≤ n).We assign all the edges of Gi(1≤i≤n)by the order of the components and trail as following:

xijand yijare the two end-points of the j-th trail in Gi,uijtis the t-th internal vertex of the j-th trail of Gi.We give labeling−1 and 1 alternatively to the above edges.The same as Theorem 3,we know that when the vertex is even,it is the internal of any trail and has labeling 0;when the vertex is odd,then it is exactly one end-point of a trail and has labeling−1 or 1.Moreover,By vf(1)−vf(−1)=2[ef(1)−ef(−1)]and G has the even number of edges we know that vf(1)=vf(−1).Thus G is semi-H-cordial.