Analysis On an SEIRS Epidemic Model with Pulse Vaccination and Two Time Delays
(School of Science,Chang’an University,Xi’an 710064,China)
Abstract:In this paper,an SEIRS epidemic model with pulse vaccination and two time delays is proposed.By using stroboscopic map and comparison principle,the disease-free periodic solution(DFPS for short)is obtained and the global asymptotic stability of the DFPS is proved.The sufficient conditions for the permanence of the model are obtained.In addition,numerical simulations are done to confirm our theoretical results.
Key words:impulsive vaccination;time delay;threshold values;global stability;permanence
§1. Introduction
The epidemic of infectious diseases is a serious threat to human health.Vaccination is one of important means to control diseases.For seasonal infectious diseases,such as poliomyelitis and epidemic encephalitis B,these can be prevented by periodic vaccination.Thus,the research with controlling disease strategy of pulse vaccination are done by lots of scholars(see[1-4]).In[5],Zhang et al studied an SIRS epidemic model with pulse vaccination.They give the sufficient conditions for the global stability of the DFPS and disease persistence.What’s more,the e ff ects of pulse vaccination and continuous vaccination on the control of disease are compared.In[6,7],the authors considered the e ff ect of latency and time delay of cure time,they studied an SEIR model with pulse vaccination and nonlinear incidence,prove the global stability of the DFPS and the persistence of the disease.In[8,9],the authors investigated a delayed epidemic model with pulse vaccination.They obtain the sufficient conditions of the disease disappearance and permanence.For some diseases such as AIDS,hepatitis B,venereal diseases with vertical transmission,although the authors have studied the delayed SEIR epidemic models with impulse vaccination,but vertical infection was not considered in their models[6-8,10].In this paper,basing on previous articles,we consider the limited time of latent period and immune time to know the impact of pulse vaccination on disease control.We establish an SEIRS epidemic model with vertical infection,impulsive vaccination,two time delays and study its dynamic properties.
The organization of this paper is as follows:In Section 1,we will establish an SEIRS epidemic model with pulse vaccination and two time delays.In Section 2,we will prove that the DFPS is globally attractive.In Section 3,we will study the permanence of disease.In Section 4,we will do numerical simulations to confirm our theoretical results.Finally,we will make a discussion for this article.
§2.Model Description
In reality,some diseases belong to vertical transmission,in order to describe this type of infectious disease model,here,S(t),E(t),I(t)and R(t)represent the number of the susceptible,the exposed,the infected,the recovered at time t,respectively.The total population number is expressed at time t by N(t)=S(t)+E(t)+I(t)+R(t).
Principle hypothesizes are as follows:
(i)We use bilinear incidence in the model[8].
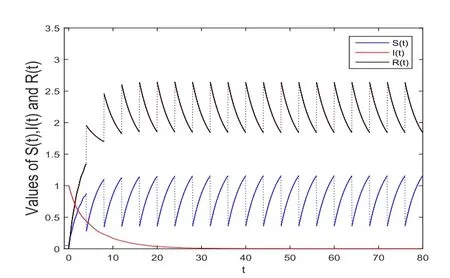
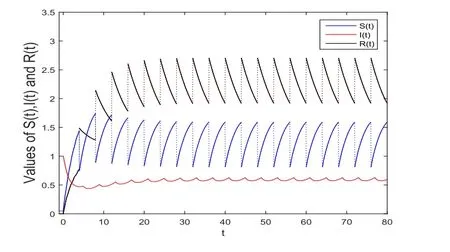
(ii)In the unit time,aA newborn infants enter the susceptible class and(1−a)A newborn infants enter the recovery class(0 (iii)Each compartment has the same natural death rateµ.Birth rate of infected individuals isµ. (iv)Only the susceptible individuals are vaccination and the vaccination rate of each susceptible individuals is p(0 (v)The infected people have vertical transmission ρ(0< ρ <1). (vi)r is the recovery rate.δ is the average loss rate of immunity obtained by a cure for the disease.ω is the latent period of the disease,τ is the immune period of the population.β is average number of adequate contact rate of an infectious individuals per unit time. With the above assumptions(i-vi),we can obtain an SEIRS epidemic model with vertical infection,impulsive vaccination and two delays: The total population size N(t)can be determined by the di ff erential equation From(2.2),we have We focus our attention only on the following model Set l=max{ω,τ}.The initial condition of system(2.3)is where φ =(φ1,φ2,φ3)T∈ PC+and PC+is the space of all piecewise functions φ :[−l,0]→with points of discontinuity at−kT(k∈N)of the first kind and which are continuous from the left,that is,φ(−kT −0)= φ(−kT),where and designates the norm of an element φ in PC+by By biological meaning,we further assume that φi(0)>0 for i=1,2,3.The meaningful domain of system(2.3)is and we can know that D is positively invariant set. Lemma 2.1[8]Consider the following equation where a,b,ω >0.x(t)>0 for t∈ [−ω,0],we have Lemma 2.2[10]Consider the following impulse di ff erential inequalities where p(t),q(t)∈C[R+,R],dk≥0 and bkare constants. Assume(A0)the sequence{tk}satisfies 0 ≤ t0 Then Lemma 2.3 Consider the following impulsive di ff erential equation where a>0,b>0,c>0,d>0 and 0<λ≤1.Then there exists a unique T-periodic solution of system(2.5) which is globally asymptotically stable.Here Proof By directly calculating,we obtain the solution of the first and second equations in system(2.5) Using the third and fourth equations of system(2.5),we can employ the stroboscopic map such that where It is easy to know that the maps f and g have unique positive fixed points,respectively,where Obviously,0 is globally asymptotically stable.The proof of Lemma 2.3 is completed. Firstly,we demonstrate the existence of the DFPS of system(2.3).When I(t)≡0,the system(2.3)can be written as follows According to Lemma 2.3,we know that the periodic solution of system(3.1)is of form where According to Lemma 2.3,(˜S(t),˜R(t))is a unique globally asymptotically stable positive periodic solution of system(3.1). Denote a quantity Theorem 3.1If<∗<1,then the DFPS(˜S(t),0,˜R(t))of system(2.3)is globally asymptotically stable in D. Proof Since<∗<1,here,we have a ε1>0 small enough such that where From the first and fourth equations of system(2.3)that According to Lemma 2.2,we get where Thus where Then which implies There exist a positive number k2≥k1such that for all t≥k2T.From(3.2)and the second equation of system(2.3),we get for all t≥k2T+ω and k>k2. Since βe−µωSM according to Lemma 2.1,we have=0.By comparison theorem and non-negativity of I(t),we get=0. Without loss of generality,we may assume that 0 We consider the following impulsive comparison system According to Lemma 2.3,we know that the periodic solution of system(3.4)is of form where There exists a k3>k2,such that On the other hand,from system(2.3),it follows that We consider the following impulsive comparison system According to Lemma 2.3,we know that the periodic solution of system(3.7)is of form where There exists a k4>k3such that From(3.5)and(3.8),we obtain that When εi→0(i=1,2,3),we get that S(t)→˜S(t),R(t)→˜R(t)(t→∞).Thus,we have proved the global attraction of the DFPS(˜S(t),0,˜R(t))of system(2.3).This completes the proof. Corollary 3.1The DFPS(˜S(t),0,˜R(t))of system(2.3)is globally attractive provided that ω > ω∗or τ> τ∗,where and Remark 3.1 Theorem 3.1 determines the global attractivity of the DFPS of system(2.3)in D for the case<∗<1.Its epidemiological implication is that the infectious population vanishes i.e.the disease dies out.Corollary 3.1 implies that the disease will disappear if the length of latent period exceeds ω∗or the length of immune period exceeds τ∗. In this section,we say the disease becomes endemic if the infectious population persists above a certain positive level for a long period. Definition 4.1 In system(2.3),the disease is said to be permanent if there is a positive constant q such thatinf I(t)≥ q for any positive solution(S(t),I(t),R(t))of system(2.3)with initial condition(2.4). Denote a quantity Theorem 4.1 If<∗>1,then the disease is permanent in system(2.3). Proof Since<∗>1,there exist two positive numbers ε4and m sufficiently small such that where We consider the following continuous function V(t) The derivative of V(t)along solutions of system(2.3)is Thus,we consider the following comparison impulsive di ff erential system According to Lemma 2.3,we know that the periodic solution of system(4.3)is of form where Thus,there exists a k1>0,satisfying for all t≥k1T.By(4.2)and(4.4),we have for all t≥k1T. This is a contradiction.Hence,we claim that I(t)≥h for all t≥t1.Combining with(4.5),we get From(4.6),we have V(t)→ +∞ as t→ +∞.Because V(t)is bounded.Therefore,this is a contradiction.We have proved the claim.Next,according to above claim,we will discuss two possibilities as follows. Case 1 I(t)≥m holds true for all t large enough; Case 2 I(t)oscillates about m for all large t. If Case 1 is true,then the disease is permanent.Therefore,we only need to consider Case 2.Let t1and t2be large sufficiently and satisfy If t2−t1≤k1T+ω,then I0(t)≥ −(r+µ+δ)I(t)and I(t1)=m imply I(t)≥me−(r+µ+δ)(k1T+ω)q for all t∈ [t1,t2].If t2−t1>k1T+ω,then it is clear that I(t)≥ q for all t∈[t1,t1+k1T+ω].We repeat above process(4.3)-(4.4)on the interval[t1,t2],we can obtain S(t)≥ S∆for all t∈[t1+k1T,t2].Next,we will prove that I(t)≥q is still valid for all t∈[t1+k1T+ω,t2].If it is not true,then there is a positive number T0such that I(t)≥q for all t∈[t1,t1+k1T+ω+T0],I(t1+k1T+ω+T0)=q and I0(t1+k1T+ω+T0)≤0.Using the second equation of system(2.3),as¯t=t1+k1T+ω+T0,we further obtain This is a contradiction.Hence,we claim that I(t)≥q is valid for all t∈[t1,t2].The proof of Theorem 4.1 is completed. Corollary 4.1The periodic solution(˜S(t),˜I(t),˜R(t))of system(2.3)will be permanent provided that ω < ω∗,where We introduce an SEIRS epidemic model with pulse vaccination and two time delays,analyze that the latent period of disease,the temporary immunity period of the recovered and pulse vaccination bring e ff ects on infection-eradication and the permanence of epidemic disease.Here,all of the parameter values are estimated and reference[8].The system(2.3)parameters are taken as: (1)T=4,ω =1,τ=4,a=0.5,A=0.9,ρ =0.15,δ=0.01,µ =0.3,β =0.15,r=0.2,p=0.7,then=0.3860<1.According to Theorem 3.1,we know that the disease will disappear(see Fig.1). (2)T=4,ω =1,τ=4,a=0.85,A=0.9,ρ =0.6,δ=0.15,µ =0.2,β =0.35,r=0.1,p=0.5 then=2.9825>1 and=1.1316>1.According to Theorem 4.1,we know that the disease will be permanent(see Fig.2). In the following,we will study the relationship betweenand immunity period of the recovered τ,latent period of the disease ω,pulse vaccination rate p and period of pulsing T on the system(2.3)by numerical analysis.We consider the hypothetical set of parameter values as a=0.5,A=0.9,ρ =0.15,δ=0.01,µ =0.3,β =0.15,r=0.2(see Fig.3). Fig.1 This Fig shows that movement paths of S,I and R as functions of time t.<∗=0.3860<1.The disease dies out Fig.2 This Fig shows that movement paths of S,I and R as functions of time t.<∗=1.1316>1.The disease is permanent Fig.3 This Fig shows that the relationship between the parameters and<∗ In this paper,we have studied an SEIRS epidemic model with pulse vaccination and two time delays.We obtain some thresholds valuesandIf<1,then the disease will be extinct,if>1 the disease will be permanent(see Fig.1 and Fig.2).What’s more,in order to further prevent the epidemic of infectious diseases,we also may appropriate increase immune period τ of the recovered,latent period ω of the disease,vaccination rate p and reduce the vaccination period T,which will lead to eradication of the disease(see Fig.3).Corollary 3.1 and 4.1 show that ω > ω∗or τ> τ∗implies the disease will fade out,whereas ω < ω∗implies that the disease will be uniformly persistent.From the expression of thresholds valueand,it can be seen that in reality,it is the most e ff ective way to prevent and control the spread of diseases by increasing pulse vaccination rate p and recovery rate r,reducing vaccination period T and contact rate β.In addition,we can raise the level of medical care,increase the rate of cure,and make the infected individuals recover from the disease as soon as possible. In Fig.2,by defining the expression of the thresholds values<,we know that further research can find out a more stringent critical condition in(<∗,<∗)to decide whether the disease is extinct or not.These works will be left as our future consideration.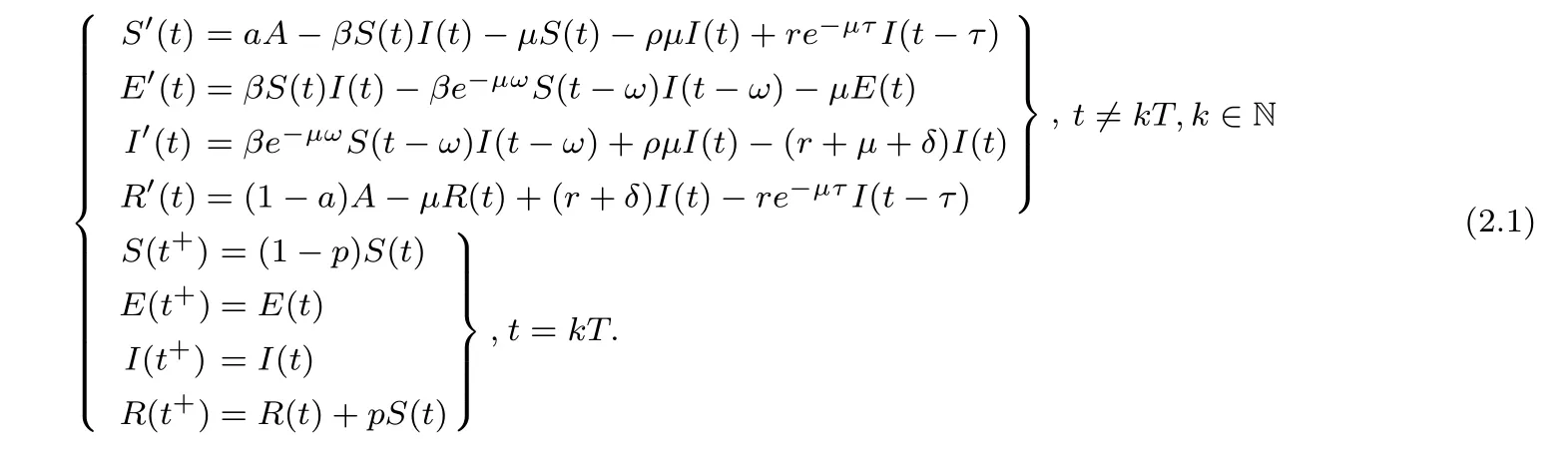

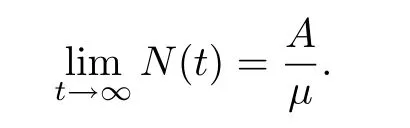

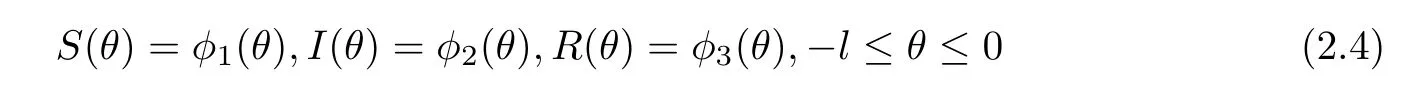
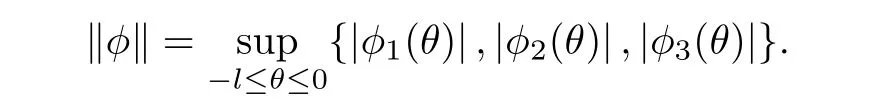

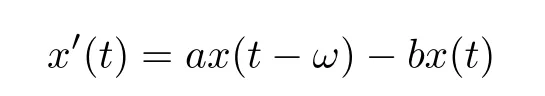
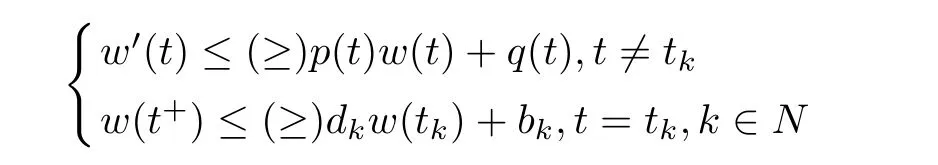
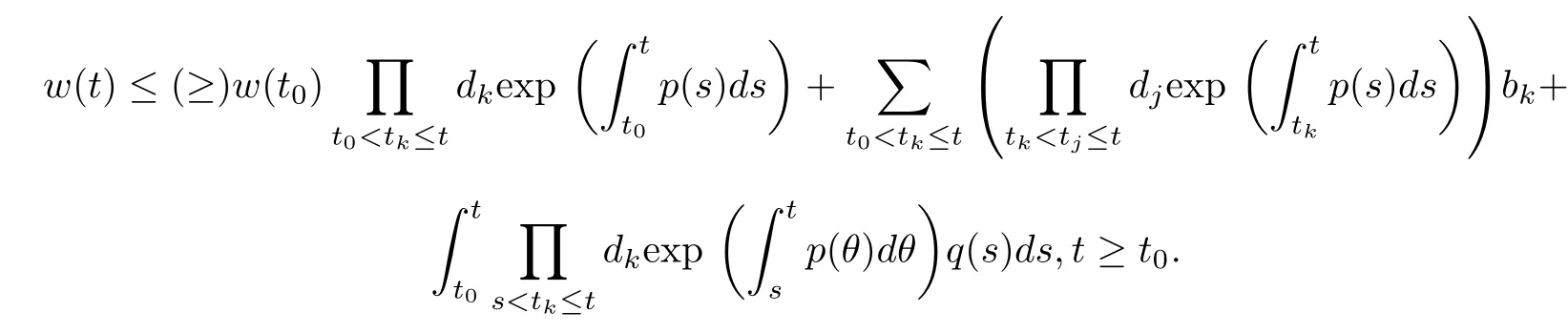
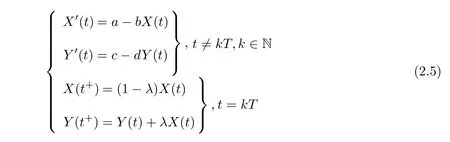
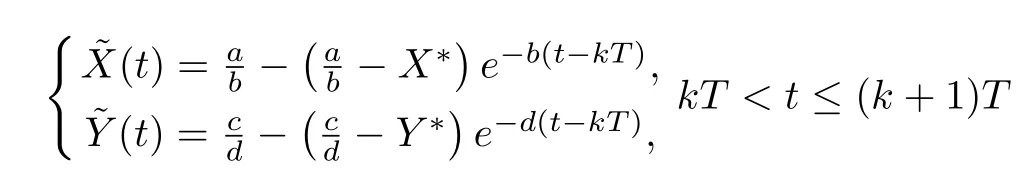


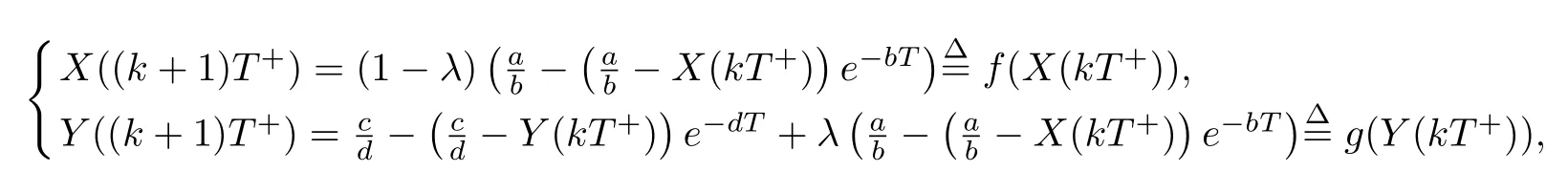
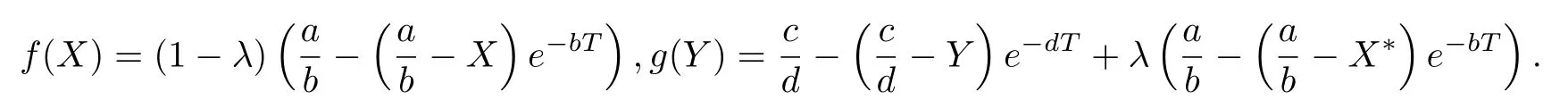
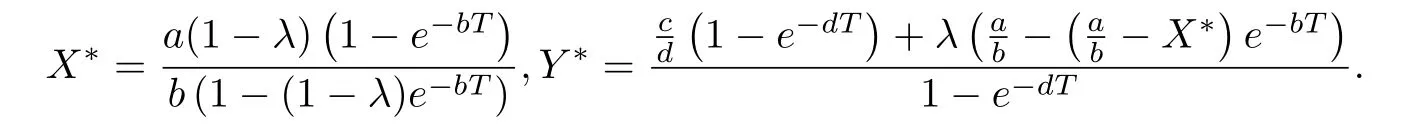
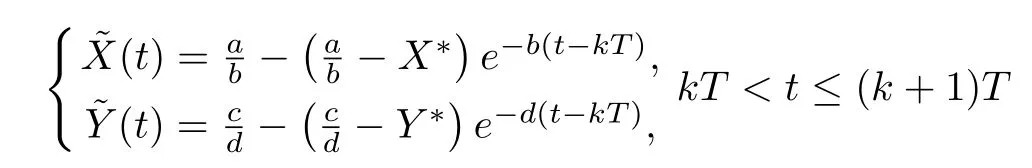
§3.Global Attractivity of The DFPS
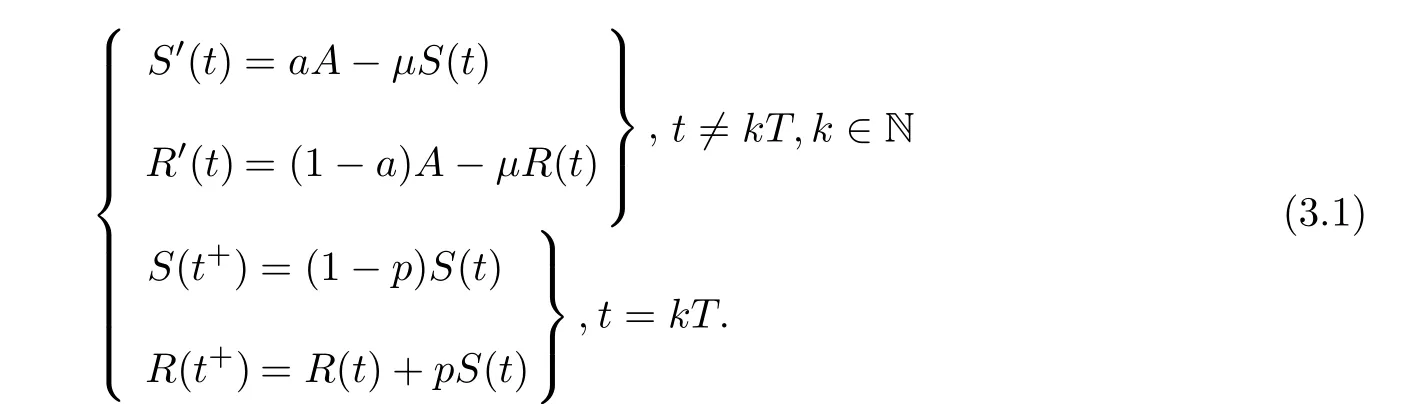

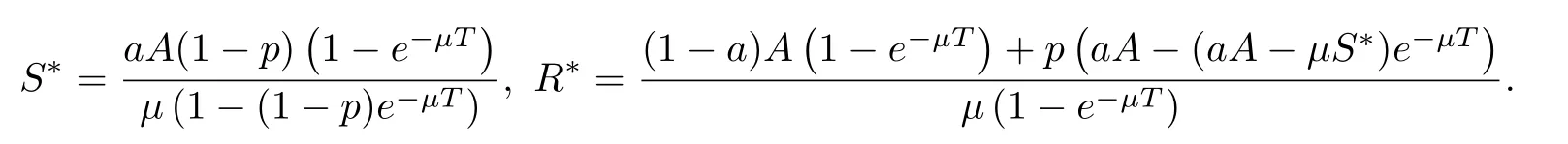

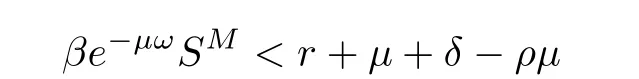

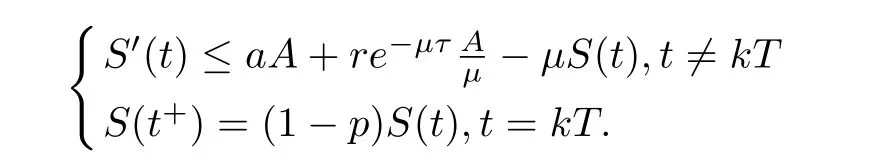
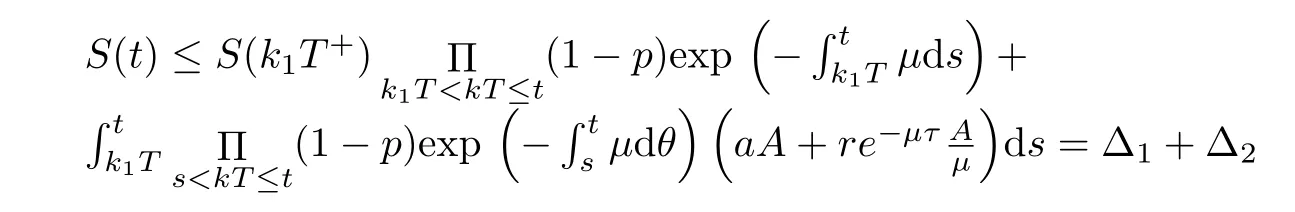
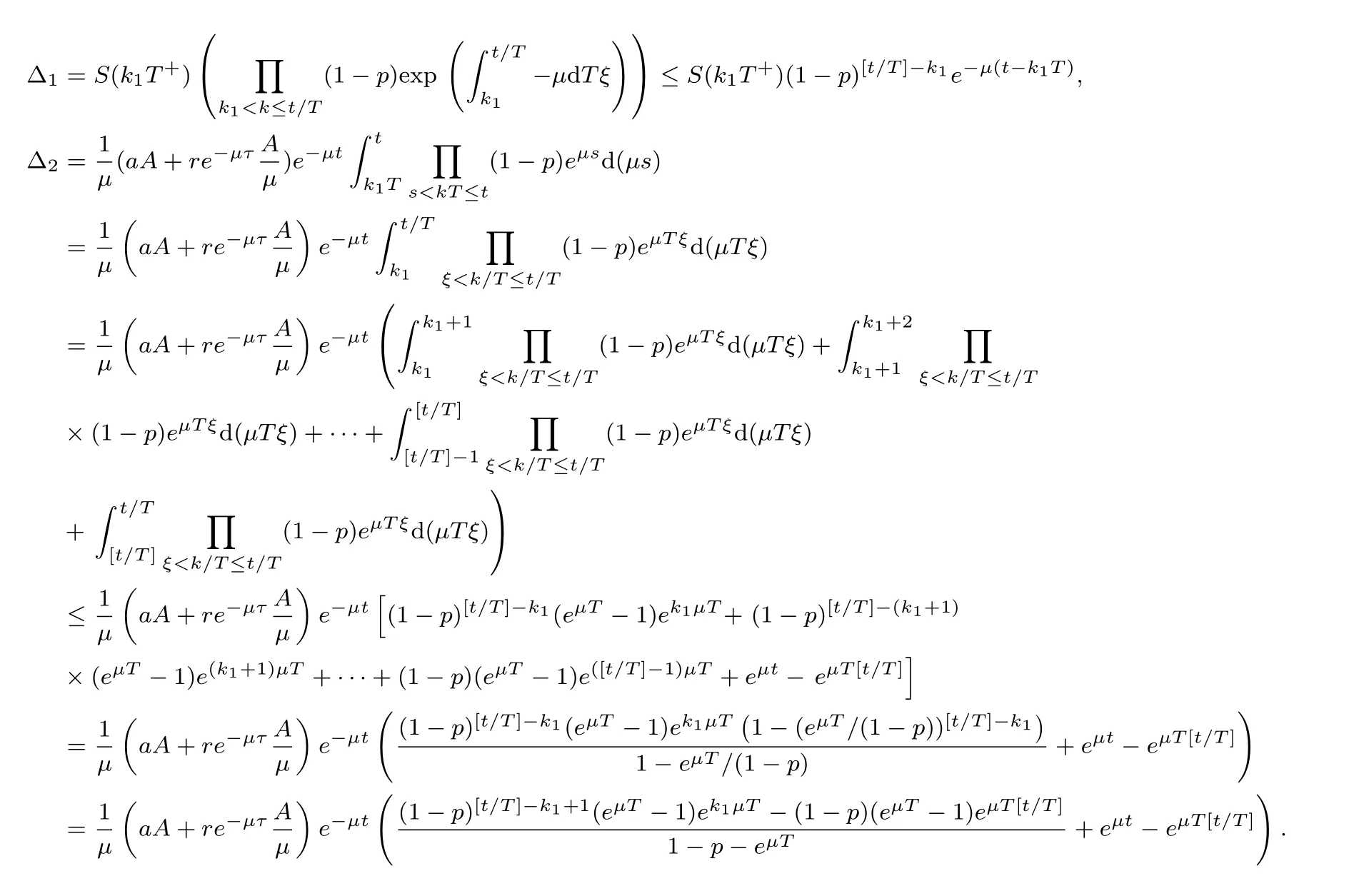
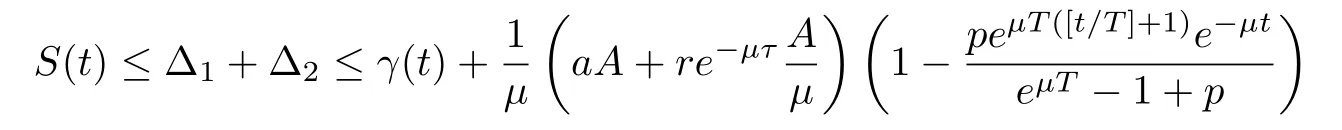
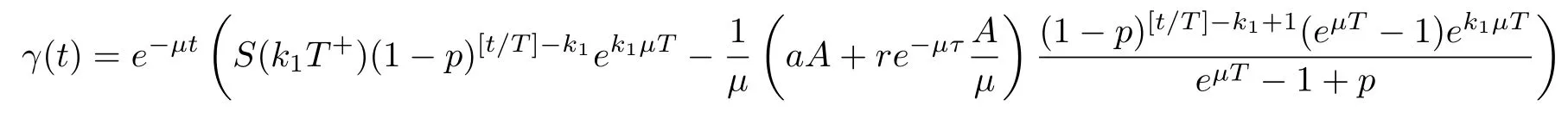

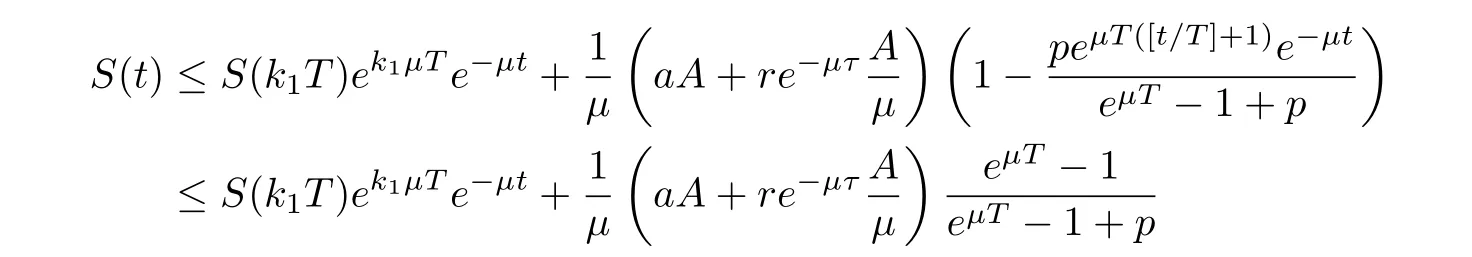
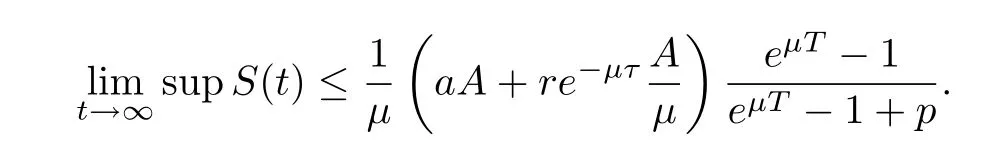
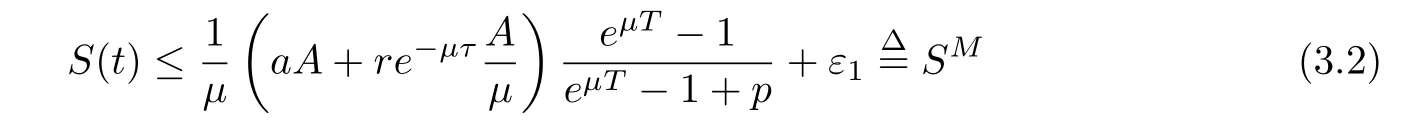
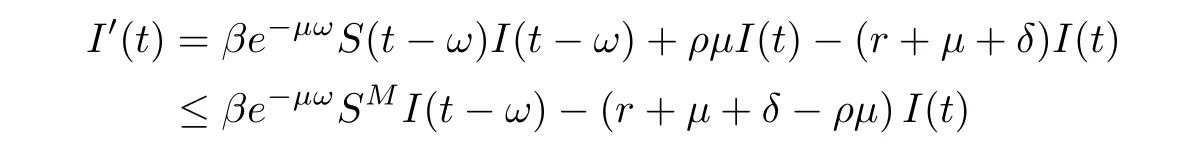
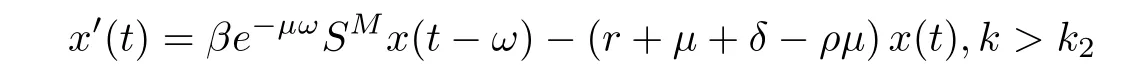
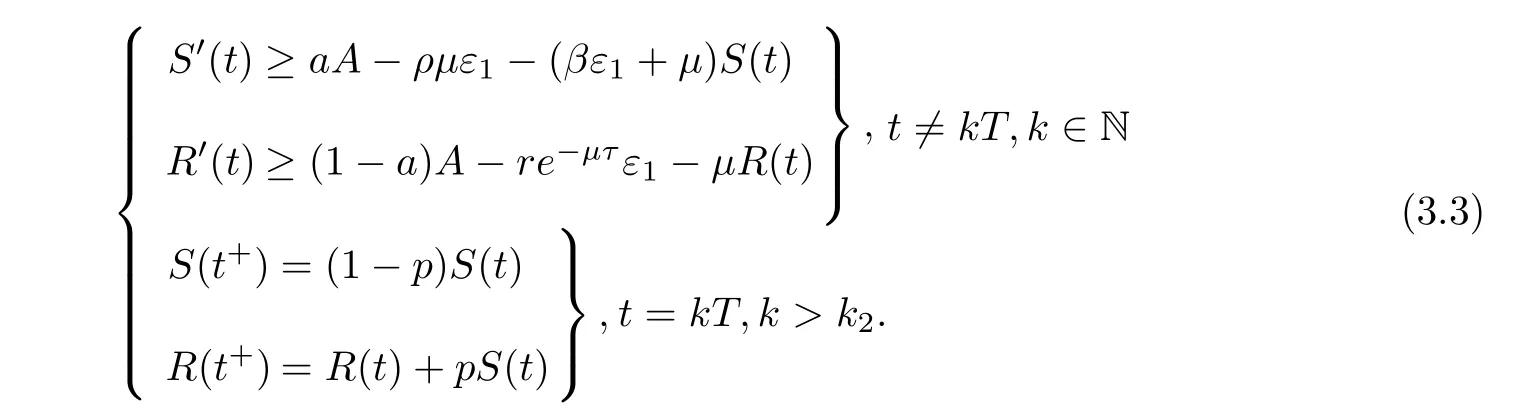
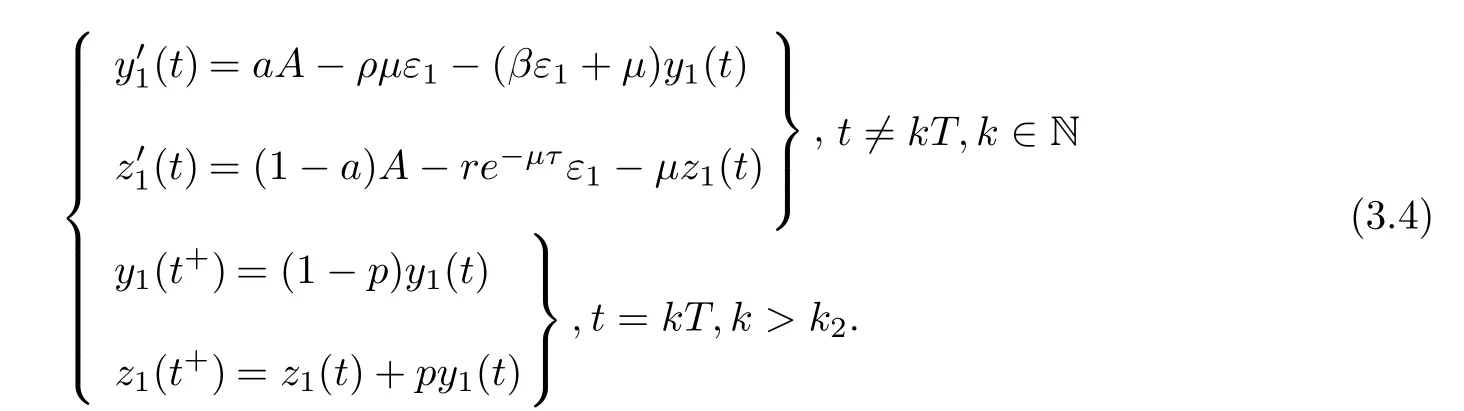

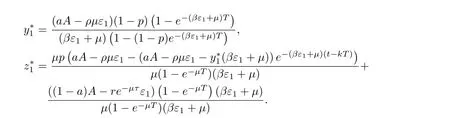
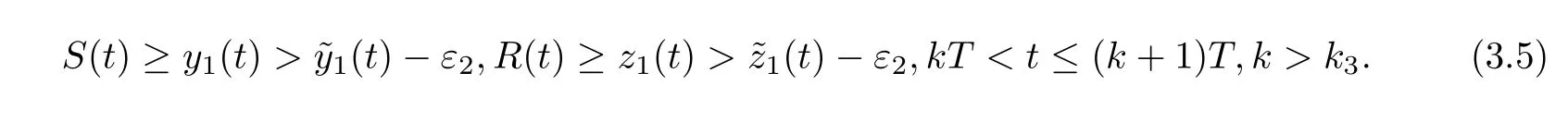

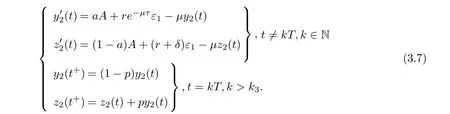
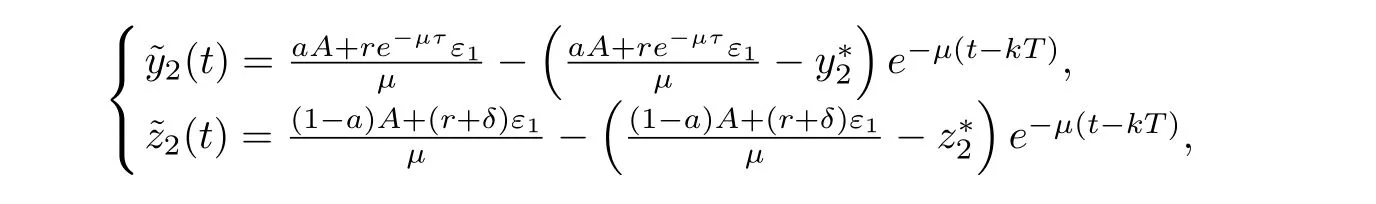



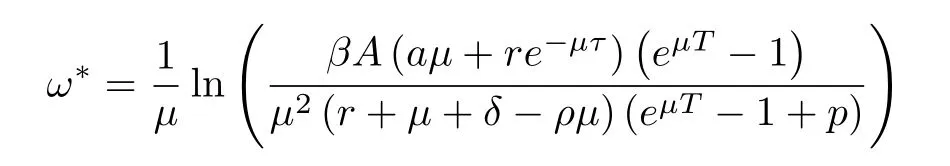
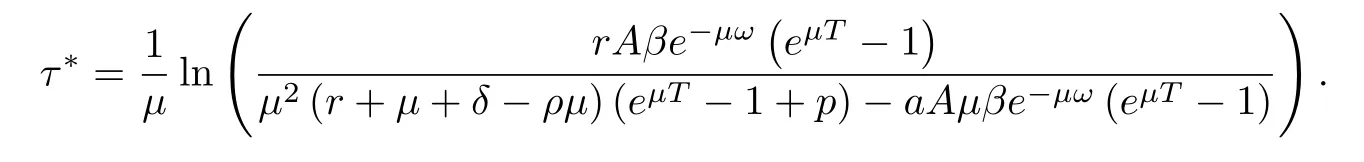
§4. Permanence of Disease



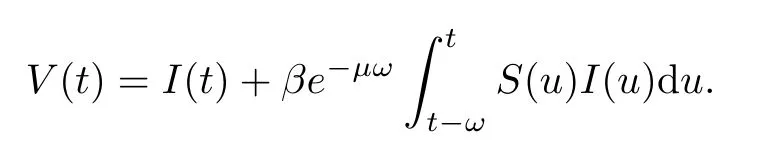
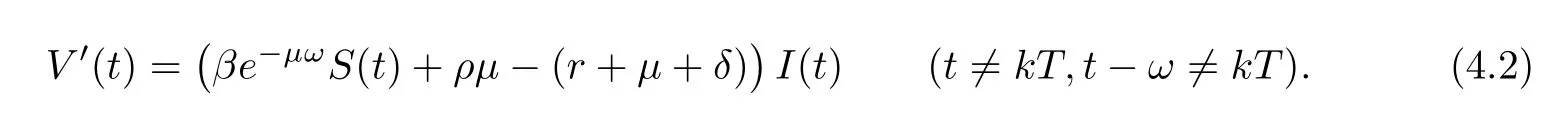
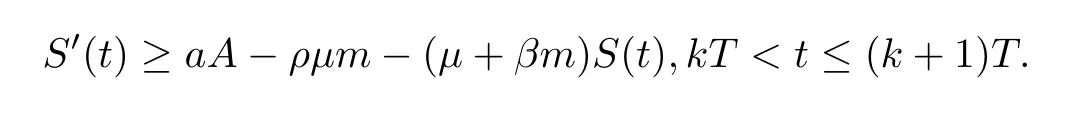

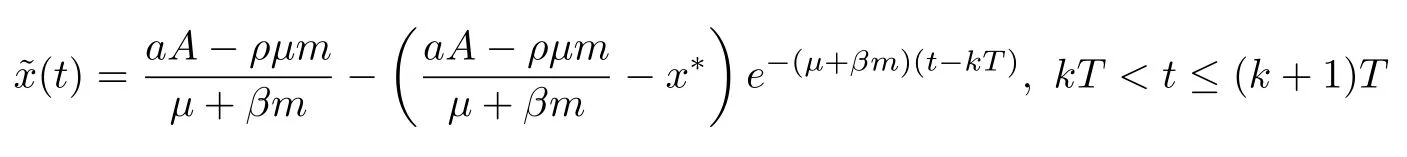
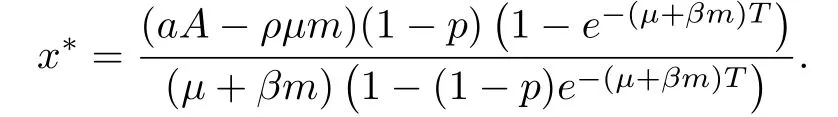



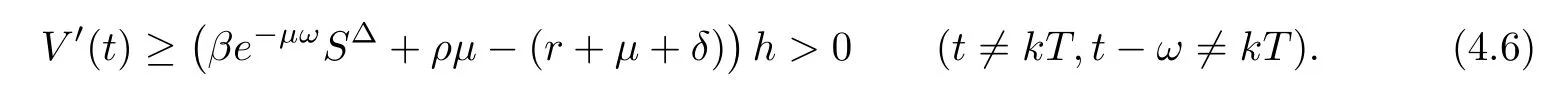



§5.Numerical Simulation
§6. Discussion
 Chinese Quarterly Journal of Mathematics2019年1期
Chinese Quarterly Journal of Mathematics2019年1期
