An Improvement in Ordered Cone b-metric Spaces Over Banach Algebras
HAN Yan,XU Shao-yuan,DONG Yan-shou
(1.School of Mathematics and Statistics,Zhaotong University,Zhaotong 657000,China;2.School of Mathematics and Statistics,Hanshan Normal University,Chaozhou,521041,China)
Abstract:The purpose of this paper is to improve some famous theorems for contractive mapping from ρ(α + β) ∈ [0,)to ρ(α + β) ∈ [0,1)in ordered cone b-metric spaces over Banach algebras with coefficient s ≥ 1(ρ(x)is the spectral radius of the generalized Lipschitz constant x).Moreover,some similar improvements in ordered cone b-metric spaces are also obtained,which from α+β ∈[0,)to α+β ∈[0,1).Some examples are given to support that our new results are genuine improvements and generalizations.
Key words:Cone b-metric spaces over Banach algebras;c-distance;generalized Lipschitz mappings;fixed point
§1. Introduction and Preliminaries
Cone metric spaces were introduced by[1],which is a generalization of metric spaces.Later on,cone b-metric space with coefficient s≥1 was introduced by[2].Many authors established various fixed point theorems in cone b-metric spaces(see[3,4,16]).However,some researchers established the equivalence between the fixed point results in metric spaces and in cone metric spaces(see[5,6]).Recently,Liu and Xu[13]defined cone metric space over Banach algebra by replacing Banach space by Banach algebra,and proved some fixed point theorems in such spaces.They also gave some examples which showed that fixed point theorems in cone metric spaces over Banach algebras are not equivalent to those in(general)metric spaces.In 2011,Cho et al.[8]proved some fixed point results under the concept of c-distance which is a cone version of w-distance of Kada et al.[9].In this paper,the existence and uniqueness of some new fixed point theorems on c-distance in ordered cone b-metric spaces over Banach algebras are obtained.The conditions α,β >0,α + β <(or k∈[0,)are instead by generalized Lipschitz constant ρ(α + β) ∈ [0,1)(or ρ(k) ∈ [0,1)).The main results improve and extend some important known results in the literature[4,7,12].Moreover,some examples are given to show that the main results are genuine improvements and generalizations of the corresponding results in the literature.
First,we recall some well-known concepts about Banach algebras and cone b-metric spaces.
Let A be a real Banach algebra,i.e.,A is a real Banach space in which an operation of multiplication is defined,subject to the following properties:for all x,y,z∈A,a∈R
(1)x(yz)=(xy)z;
(2)x(y+z)=xy+xz and(x+y)z=xz+yz;
(3)a(xy)=(ax)y=x(ay);
In this paper,we shall assume that the Banach algebra A has a unit(i.e.,a multiplicative identity)e such that ex=xe=x for all x∈A.An element x∈A is said to be invertible if there is an inverse element y∈ A such that xy=yx=e.The inverse of x is denoted by x−1.For more details,we refer to[15].
The following proposition is well known(see[15]).
Proposition 1.1 Let A be a real Banach algebra with a unit e and x∈A.If the spectral radius ρ(x)of x is less than 1,i.e.,
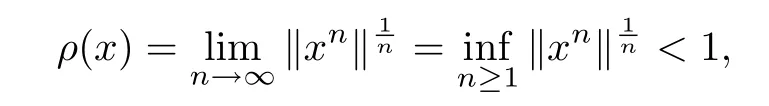
then e−x is invertible.Actually,
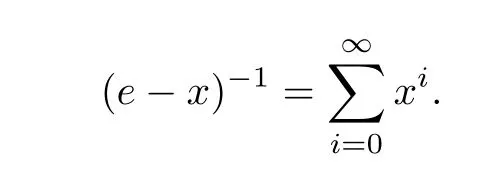
Remark 1.2 If ρ(k)<1 then→ 0(n→ ∞).
A subset P of A is called a cone if:
(i)P is non-empty,closed and{θ,e} ⊂ P,where θ denotes the zero element of A;
(ii)αP+βP ∈ P for all non-negative real numbers α,β;
(iii)P2=PP⊂P;
(iv)P ∩ (−P)={θ}.
For a given cone P⊂A,we can define a partial orderingwith respect to P by xy if and only if y−x∈P.We shall write x≺y if xy and x 6=y,while x¿y will stand for y−x∈intP,where intP denotes the interior of P.A cone P is called normal if there is a number K>0 such that for all x,y∈A,θxy implies≤K.The least positive number satisfying the above inequality is called the normal constant of P.
In the following we always assume that P is a cone in Banach algebra A with intP 6=∅andis the partial ordering with respect to P.
Definition 1.3[2],[3]Let X be a nonempty set,s≥1 be a constant,and A be a Banach algebra.Suppose that the mapping d:X×X→A satisfies:
(d1)θ„d(x,y)for all x,y∈X and d(x,y)=θ if and only if x=y;
(d2)d(x,y)=d(y,x)for all x,y∈X;
(d3)d(x,y)„s[d(x,z)+d(z,y)]for all x,y,z∈X.
Then d is called a cone b-metric on X and(X,d)is called a cone b-metric space over Banach algebra A.
Definition 1.4[4]Let(X,d)be a cone b-metric space over a Banach algebra A,and s≥1 be a constant.Then the mapping q:X×X→A is called a generalized c-distance on X if the following conditions are satisfied:
(q3)for each x∈X and n≥1,if q(x,yn)u for some u=ux∈P,then q(x,y)su whenever{yn}is a sequence in X converging to a point y∈X;
(q4)for all c∈ A with θ¿ c,there exists q∈ A such that q(z,x)¿ w and q(z,y)¿ w imply d(x,y)¿c.
Remark 1.5[8]The following facts are well-known.
(1)q(x,y)=q(y,x)does not necessarily hold for all x,y∈X.
(2)q(x,y)=θ is not necessarily equivalent to x=y for all x,y∈X.
(3)The c-distance is a great generalization of the w-distance.
(4)If q(x,y)=d(x,y),then q is a c-distance.That is,c-distance is also a generalization of cone metric.
Definition 1.6[7]Let(X,)be a partially ordered set.We say that x,y∈X are comparable if xy or yx holds.Similarly,f:X→X is said to be comparable if for any comparable pair x,y∈X,fx,fy are comparable.
Lemma 1.7[14]Let A be a Banach algebra with a unit e,P be a solid cone in A and„be the semi-order generated by the cone P.Let λ ∈ P.If ρ(λ)<1,then for any u ´ θ,we have uλu.
§2.Main Results
We will call a sequence{un}in P a c-sequence if for each c?θ there exists n0∈N such that un¿ c for n ≥ n0.If{un}and{vn}are c-sequences and α,β >0,then{αun+βvn}is a c-sequence.A c-sequence is a θ-sequence when the cone P is normal.If the cone is not normal,a c-sequence need not be a θ-sequence(see[11]).
Lemma 2.1[14]Let P be a solid cone in A and let{un}be a c-sequence in P.Suppose that k∈P is an arbitrary given vector.Then{kun}is a c-sequence.
Lemma 2.2 Let(X,d)be a cone b-metric space over Banach algebra A and q be a generalized c-distance on X.Let{xn}and{yn}be sequences in X and x,y,z∈X.Suppose that{un}and{vn}are two c-sequences in P.Then the following hold:
(1)If q(xn,y)unand q(xn,z)vnfor n∈N,then y=z.In particular,if q(x,y)=θ and q(x,z)=θ,then y=z.
(2)If q(xn,yn)unand q(xn,z)vnfor n∈N,then{yn}converges to z.
(3)If q(xn,xm)unfor m>n,then{xn}is a Cauchy sequence in X.
(4)If q(y,xn)unfor n∈N,then{xn}is a Cauchy sequence in X.
Proof As the proof is similar to the case of c-distance in tvs-cone metric spaces in[11],we omit it.
(i)there exist two generalized Lipschitz constants α,β ∈ P with ρ(α + β)<1 such that

for any comparable pair x,y∈X;
(ii)there exists x0∈X such that x0,fx0are comparable;
(iii)if a sequence{xn}converges to x in X and xi,xi+1are comparable for all i≥1,then xi,x are comparable.
Then f has a unique fixed point.
Proof If x0=fx0,then x0is the fixed point in X.Suppose that x06=fx0.By condition(ii)and f is comparable,we have xi=fix0and xi+1=fi+1x0=fxiare comparable for any i≥0.Now,there are three cases for the proof.

Let h= α + β.Since ρ(sh)=sρ(h)<1,then by Proposition 1.1,we get e − sh is invertible.Further more(e−sh)−1=.Thus,for any m>n≥1,we have
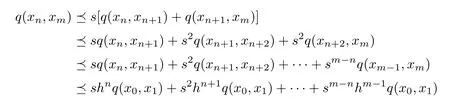
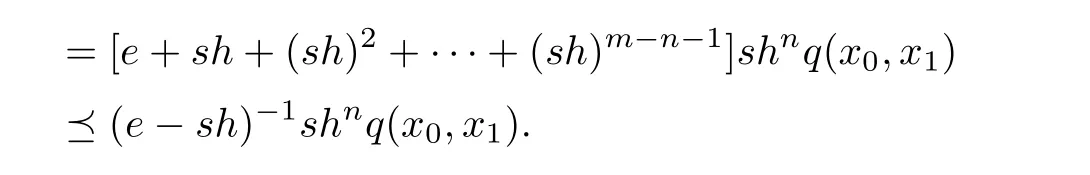
By the fact that{(e−sh)−1shnq(x0,x1)}is a c-sequence(khnk→ 0,n→ ∞).According to Lemma 2.2(3),{xn}is a Cauchy sequence in(X,d).
Since X is complete,there exists u∈X such that xn=fxn−1→ u as n→ ∞.From Definition 1.4(q3),we have
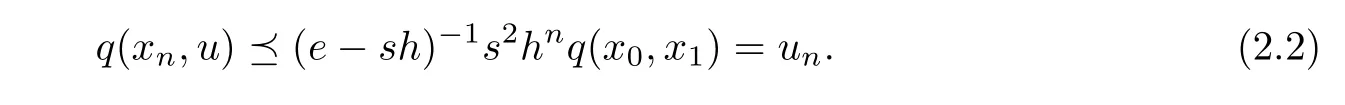
By(2.1)and the condition(iii),it follows that
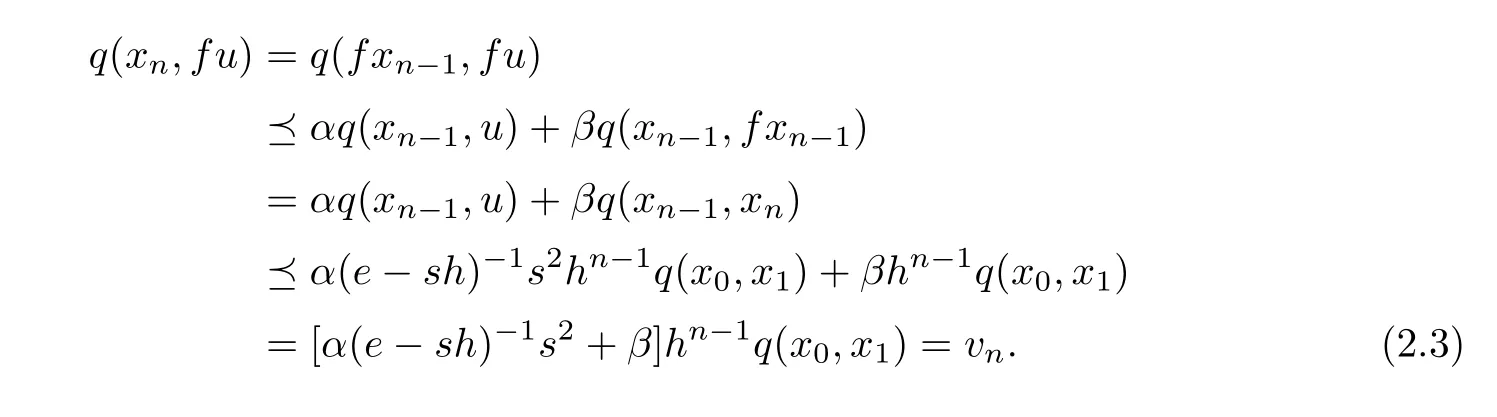
Therefore,{un}and{vn}are c-sequences.Thus,by(2.2),(2.3)and Lemma 2.1,2.2(1),we get that fu=u.
Moreover,we prove that the fixed point is unique.Firstly,we have to prove q(u,u)=θ.In view of(2.1),
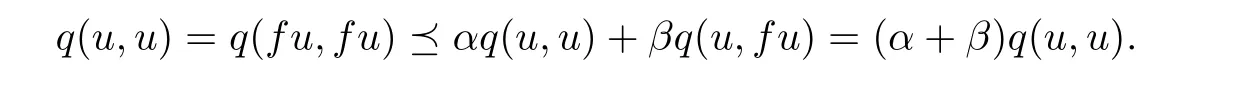
By ρ(α + β)<1 and Lemma 1.7,we have q(u,u)= θ.Secondly,if there is another fixed point v,then from(2.1),we find
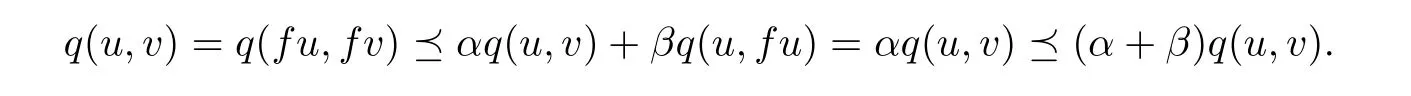
As ρ(α + β)<1,it follows immediately from Lemma 1.7 that q(u,v)= θ.Therefore,u=v is deduced by Lemma 2.2(i).The conclusion is true.
Firstly,since f is comparable,then for any comparable x,y∈X and∀k∈N,k≤n0,
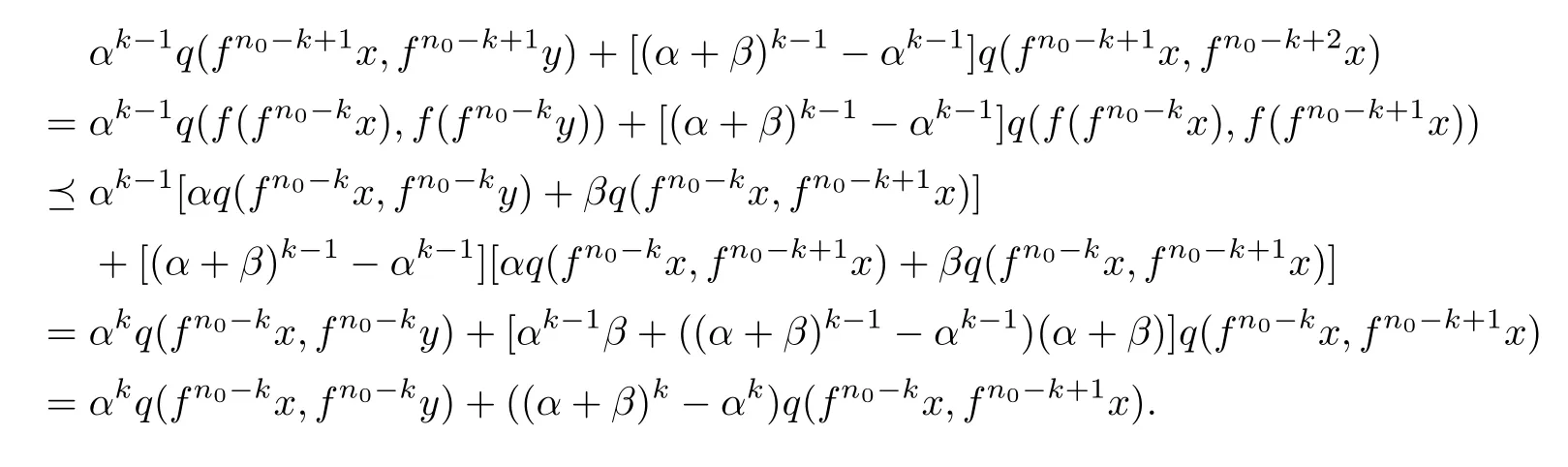
It follows that
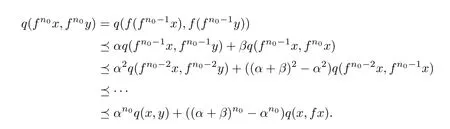
From Proposition 1.1,we have

According to Case 1,we deduce that the mapping fn0has a unique fixed point w∈X.Then,let us show that w is a fixed point of f.In fact,by fn0w=w,we obtain
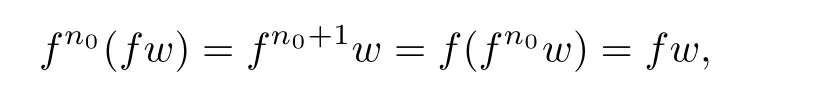
which imply that fw is also a fixed point of fn0.It is a contraction unless fw=w.The proof of the uniqueness for the fixed point is similar to that in Case 1.Hence,we omit it.
Case 3 s=1.As ρ(α + β)<1,repeating the process of Case 1,the conclusion is true.
(i)there exists a generalized Lipschitz constant α ∈ P with ρ(α)<1 such that
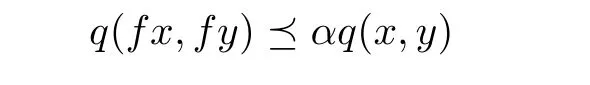
for any comparable pair x,y∈X;
(ii)there exists x0∈X such that x0,fx0are comparable;
(iii)if a sequence{xn}converges to x in X and xi,xi+1are comparable for all i≥1,then xi,x are comparable.
Then f has a unique fixed point.
Corollary 2.5 Let(X,v)be a partially ordered set.Suppose that(X,d)is a complete cone b-metric space and the underlying solid cone P.Let q be a generalized c-distance on X.Suppose the mapping f:X→X is comparable and satisfies the following conditions:
(i)there exist two constants α,β ≥ 0 with α + β <1 such that
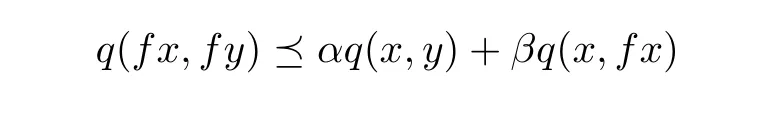
for any comparable pair x,y∈X;
(ii)there exists x0∈X such that x0,fx0are comparable;
(iii)if a sequence{xn}converges to x in X and xi,xi+1are comparable for all i≥1,then xi,x are comparable.
Then f has a unique fixed point.
Remark 2.6 Corollary 2.5 greatly improves and extends[4,Theorem 2.6]in the following two assertions.Firstly,the conditions a,b≥0,a+b Remark 2.7 Since cone b-metric spaces with Banach algebras is not equivalent to(general)b-metric spaces(see[3]),our results in this paper are focused on fixed point theorems in cone b-metric spaces over Banach algebras,which is more meaningful than theorems in usual b-metric spaces or cone b-metric spaces(see[4,10,16]). Now,we will give some examples of the situation when our theorems can be applied,while the results in the literature cannot. Further more,Consider the mapping f:X→X defined by fx=where x∈X.Obviously,f is comparable.For∀x,y∈X, Therefore,the conditions of Theorem 2.3 are satisfied and the mapping f has a unique fixed point 0 in X.Obviously,[4,Theorem 2.6]is not applicable in this example,which shows that the main results in our paper are actual generalization of the known results. Example 3.2 Let X=R,E=R2and p≥3 be a constant.Let P={x,y∈E:x≥0,y≥0}and q(x,y)=d(x,y)=(|x−y|p,|x−y|p)for all x,y∈X.Then(X,d)is a complete cone b-metric space with coefficient s=2p−1.Set the partial ordering v defined by x v y⇔x≤y.Define a mapping f:X→X by:fx=arctan(2+|x|)+x where x∈X.Obviously,there exist 0 ∈ X such that 0 v f0 and f is comparable.Take α =0.7p,β =0.We deduce that Further more,For∀x,y∈ X, Therefore,α+β=0.7p∈[,1)(p≥3).All the conditions of Corollary 2.5 are fulfilled.By Corollary 2.5,f has a unique fixed point in X.§3. Applications
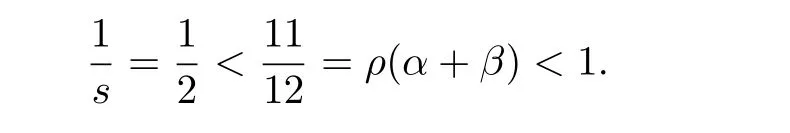
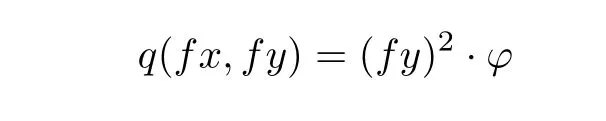

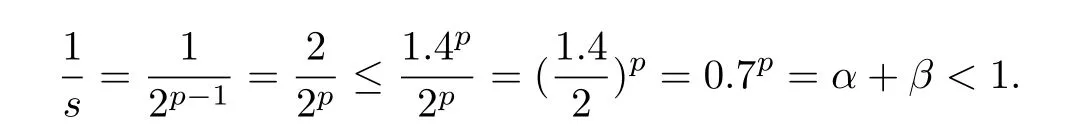

 Chinese Quarterly Journal of Mathematics2019年1期
Chinese Quarterly Journal of Mathematics2019年1期
- Chinese Quarterly Journal of Mathematics的其它文章
- A Remark on Double Ore Extensions
- Lyapunov-type Inequalities For A System of Nonlinear Di ff erence Equations
- Analysis On an SEIRS Epidemic Model with Pulse Vaccination and Two Time Delays
- The Cohomology Structures of Partial Entwining Structures
- Study On the Impact of Open Residential Block on Urban Traffic Congestion Based on Dynamic Com-prehensive Evaluation Model
- Some Results on H-cordial Graphs and Semi-H-cordial Graphs
