Lyapunov-type Inequalities For A System of Nonlinear Di ff erence Equations

(Department of Mathematics,Huaihua University,Huaihua,Hunan 418008,China)

Abstract:This paper establishes several new Lyapunov-type inequalities for the system of nonlinear di ff erence equations

Key words:Lyapunov-type inequality;Linear di ff erence system;Nonlinear di ff erence system;Hamiltonian di ff erence system

§1. Introduction

Consider the system of nonlinear di ff erence equations

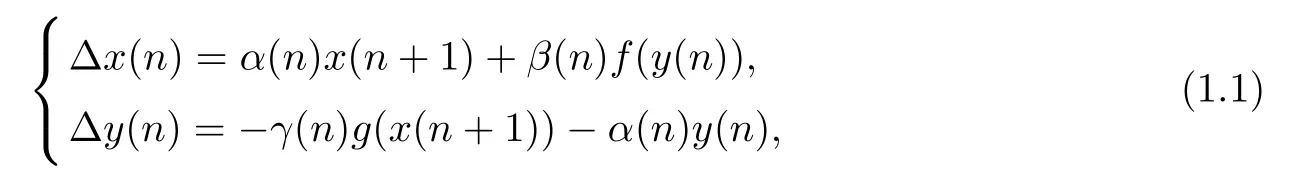
where∆ denotes the forward di ff erence operator defined by∆x(n)=x(n+1)−x(n),α(n),β(n)and γ(n)are real-valued functions defined on Z,f and g are real-valued functions defined on R.Throughout this paper,we always assume that

When f(y)≡y and g(x)≡x,system(1.1)reduces to the linear Hamiltonian di ff erence system

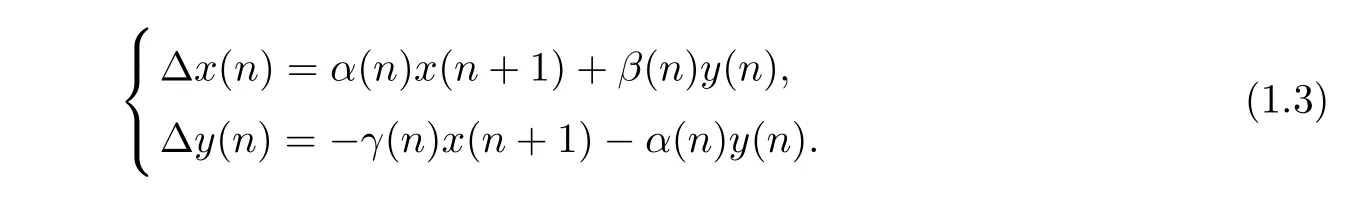
where the coefficient α(n)satisfying the condition α(n)6=1 for all n ∈ Z.In recent papers[1-8],some dynamical behaviors of solutions of system(1.3)have been discussed,such as the existence of periodic solutions,strong limit points,Weyl-Titchmarsh theory,spectral theory,eigenvalue problems and disconjugacy.We remark that system(1.1)contains many well-known di ff erence equations as special cases,such as the following second-order nonlinear di ff erence equations

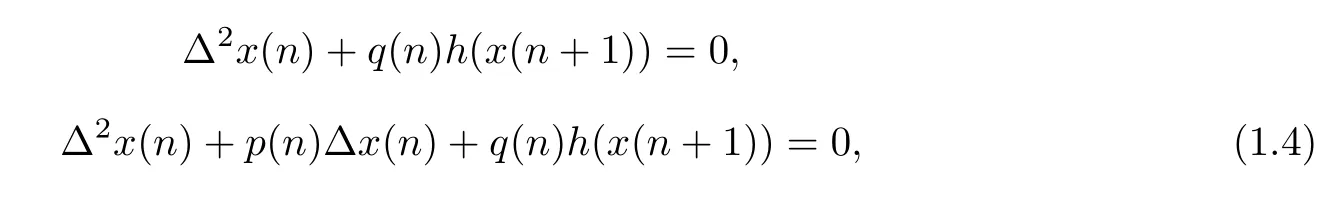
and

where p(n),q(n)and ρ(n)are real-valued functions defined on Z and h(x)are real-valued functions defined on R with ρ(n)>0 for all n ∈ Z.For example,if p(n)6=1 for all n ∈ Z,let x(n)be a solution of(1.4)and set

then(1.4)can be written in the form of(1.1):

In the discrete case,instead of usual zero,we adopt the following concept of generalized zero,which is due to Hartman[9].

Definition 1.1[9]A function h:Z→R is said to have a generalized zero at n0∈Z provided either h(n0)=0 or h(n0)h(n0+1)<0.It is a classical topic for us to study Lyapunov-type inequalities which have proved to be very useful in oscillation theory,disconjugacy,eigenvalue problems and numerous other applications in the theory of di ff erential and di ff erence equations.In the recent years,there are many literatures which improved and extended the classical Lyapunov inequality for linear or half-linear Hamiltonian systems including continuous and discrete cases.Here we only mention some references[9-23].A thorough literature review of continuous and discrete Lyapunov inequalities and their applications can be found in the survey paper[14]by Cheng and the references quoted therein.

In paper[17],Guseinov and Kaymakcalan researched linear Hamiltonian di ff erence system(1.3)and obtained the following interesting Lyapunov-type inequality results.

Theorem 1.1[17]Let a,b∈Z with a≤b−2.Assume that(1.3)has a real solution(x(n),y(n))such that x(a)=x(b)=0 and x(n)is not identically zero on[a,b].Then there holds

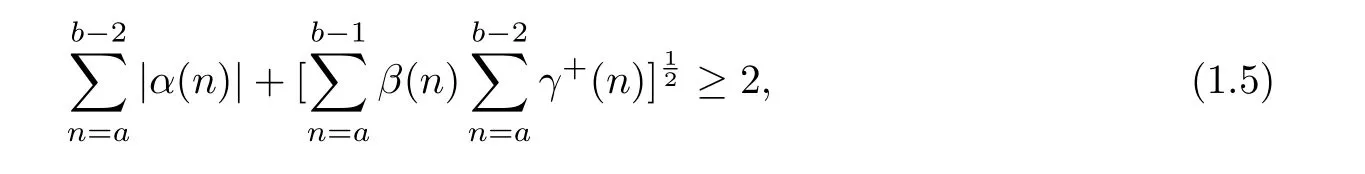
where and in the sequel

Theorem 1.2[17]Suppose that

and let a,b∈Z with a≤b−2.Assume that(1.3)has a real solution(x(n),y(n))such that x(n)has generalized zeros at a and b,and x(n)is not identically zero on[a,b],i.e.

Then one has the following inequality

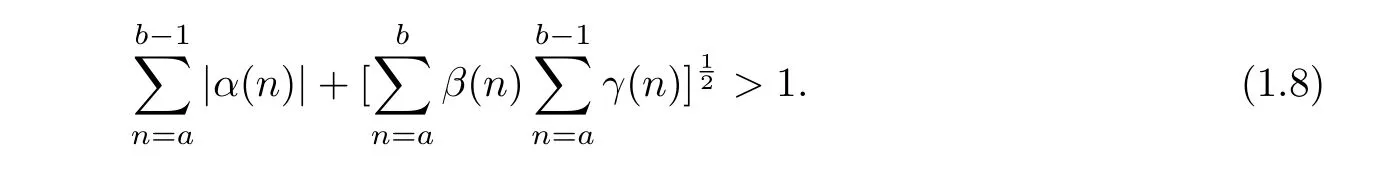
In paper[21],the authors improved the above result and obtained a better Lyapunov-type inequality than(1.8).

Theorem 1.3[21]Suppose that

and let a,b∈Z with a≤b−1.Assume that(1.3)has a real solution(x(n),y(n))such that(1.7)holds.Then one has the following inequality

Recently,[22]by He et al.and[23]by Unal et al.studied nonlinear system

However,as far as the author knows,there are little papers[22,23]which studied Lyapunovtype inequality for nonlinear di ff erence systems.Motivated by the works in[17,21,22],the purpose of this paper is to investigate the system of nonlinear di ff erence equations(1.1)and present some new Lyapunov-type inequalities.The Lyapunov-type inequalities obtained in this paper extend/supplement and improve results mentioned above.In fact,in[22],the authors studied the system(1.11)which is a class of”superlinear” case(i.e.,µ ≥ 2 or ν≥ 2),but,in this paper,we are concerned with system(1.1)where f and g are of sublinear case(See condition(H)in section 2).Thus,in certain sense,our results extend/supplement the results in[22].Also,the system(1.1)is more general in the sense that nonlinearities are given by functions f and g and therefore includes certain equations as special cases.When f(x)≡x and g(x)≡x,our results improve the results in[17](See Remark 2.1 and Remark 2.2).

§2. Main Results

In this section,we establish some new Lyapunov-type inequalities for system(1.1).

In connection with the nonlinear functions f and g,we assume that

(H) there are constants M>0 and m>0 such that

Theorem 2.1 Suppose that(1.9)and(H)hold and let a,b∈Z with a≤b−1.Assume that(1.1)has a real solution(x(n),y(n))such that(1.7)holds.Then one has the following inequality

Proof It follows from(1.7)that there exist ξ,η ∈ [0,1)such that

and

Multiplying the first equation of(1.1)by y(n)and the second one by x(n+1),and then adding,we get

Summing equation(2.4)from a to b−1,we can obtain

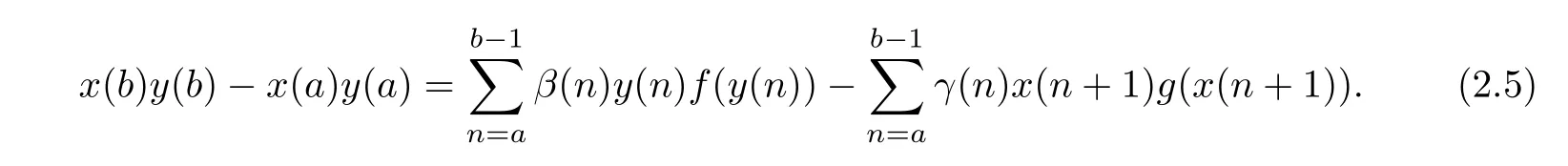
From the first equation of(1.1),we have

Combining(2.6)with(2.2),we have

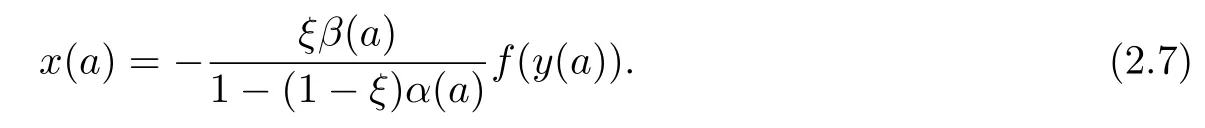
Similarly,it follows from(2.6)and(2.3)that

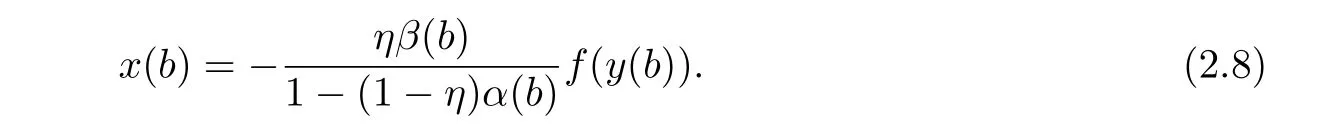
Substituting(2.7)and(2.8)into(2.5),we have

which implies that

Denote that

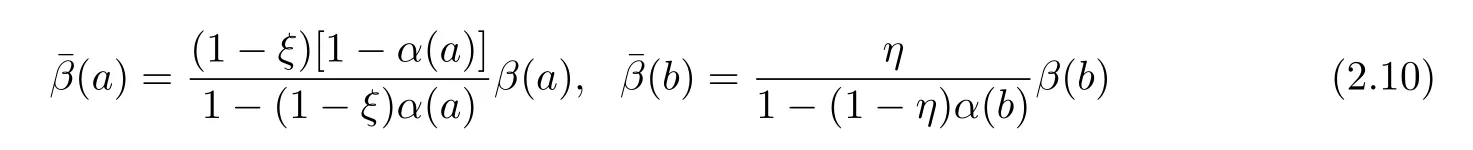
and

Then we can rewrite(2.9)as

On the other hand,summing the first equation of(1.1)from a to τ− 1 and using(2.7),we obtain

Similarly,summing the first equation of(1.1)from τ to b− 1 and using(2.8),we have

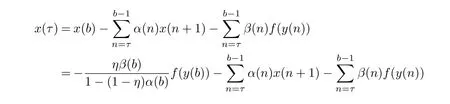
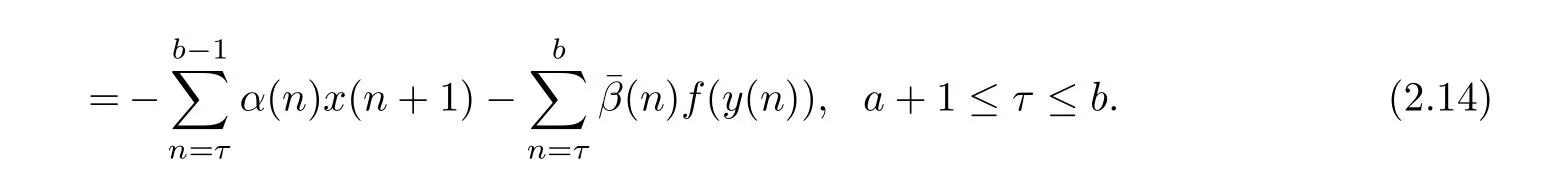
It follows from(2.13)and(2.14)that

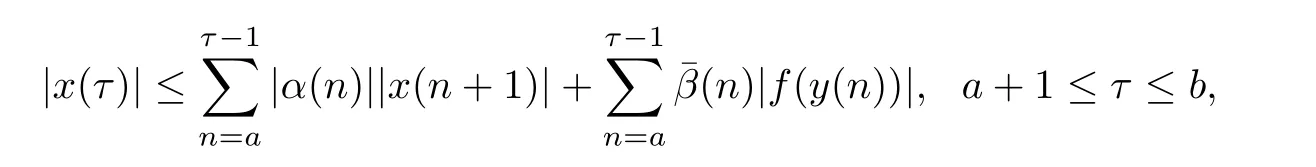
and

Adding the above two inequalities,we have

Let|x(τ∗)|=maxa+1≤n≤b|x(n)|.Applying the Cauchy-Schwarz inequality and using(H)and(2.12),we have

Dividing the latter inequality of(2.16)by|x(τ∗)|,we obtain

Since¯β(n)≤β(n)for a≤n≤b,then(2.1)follows immediately from(2.17).The proof is completed.

In the case x(b)=0,i.e.η=0,we have the following equation

and inequality

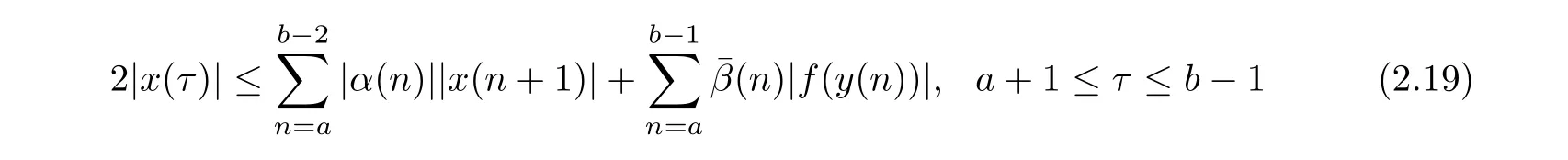
instead of(2.12)and(2.15),respectively.Similar to the proof of(2.17),we have

Therefore,we have the following theorem.

Theorem 2.2 Suppose that(1.9)and(H)hold and let a,b∈Z with a≤b−2.Assume that(1.1)has a real solution(x(n),y(n))such that x(a)=0 or x(a)x(a+1)<0 and x(b)=0 and x(n)is not identically zero on[a,b].Then inequality(2.21)holds.

Remark 2.1 when f(y)≡y and g(x)≡x,i.e.M=m=1,by(2.1)we obtain(1.10),which implies that Theorem 2.1 extends Theorem 1.3 and greatly improves Theorem 1.2.

Remark 2.2 when f(y)≡y and g(x)≡x,i.e.M=m=1,it follows from(2.21)that

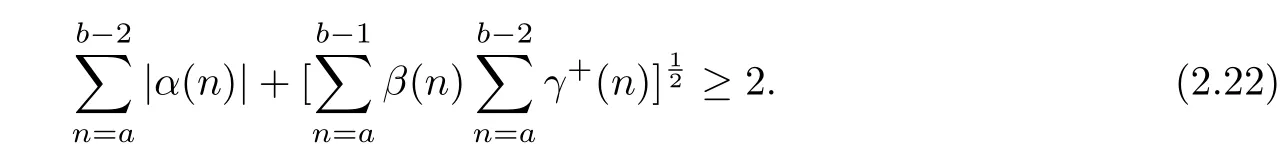
We obtain the same Lyapunov type inequality(2.22)as(1.5)under weaker assumptions than the ones of Theorem 1.1,which implies that Theorem 2.2 extends and improves greatly Theorem 1.1.Also,(2.22)improves greatly the following inequality

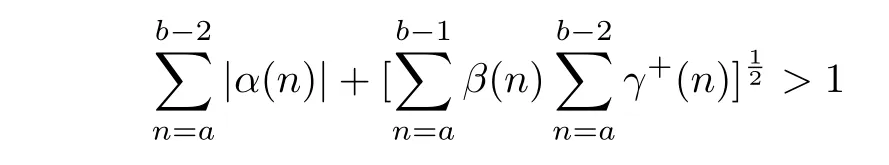
obtained in[17,Theorem 1.3].

Theorem 2.3 Suppose that(1.9)and(H)hold and let a,b∈Z with a≤b−1.Assume that(1.1)has a real solution(x(n),y(n))such that x(a)=0 or x(a)x(a+1)<0 and(x(b),y(b))=(λ1x(a),λ2y(a))with 0 ≤ λ21≤ λ1λ2≤ 1 and x(n)is not identically zero on[a,b].Then one has the following inequality

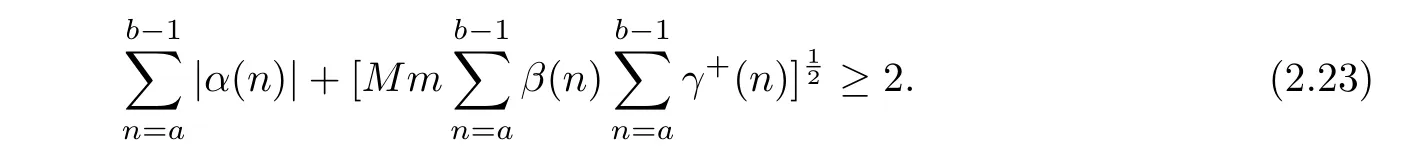
Proof It follows from the assumption x(a)=0 or x(a)x(a+1)<0 that there exists ξ∈[0,1)such that(2.2)holds.Further,by the proof of theorem 2.1,(2.4)-(2.7)hold.Since(x(b),y(b))=(λ1x(a),λ2y(a)),by(2.5),we have

Substituting(2.7)into(2.24),we have

which implies that

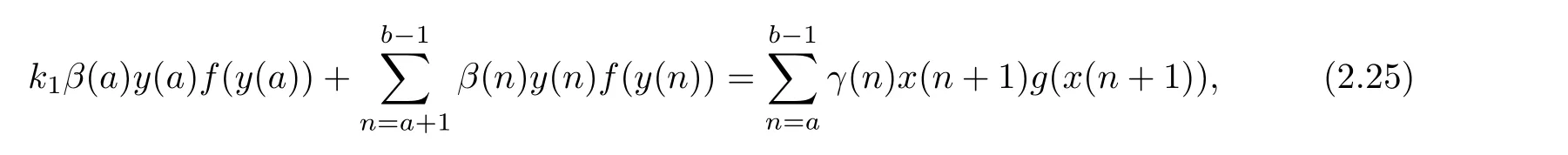
where

On the other hand,summing the first equation of(1.1)from a to τ− 1 and using(2.7),we obtain

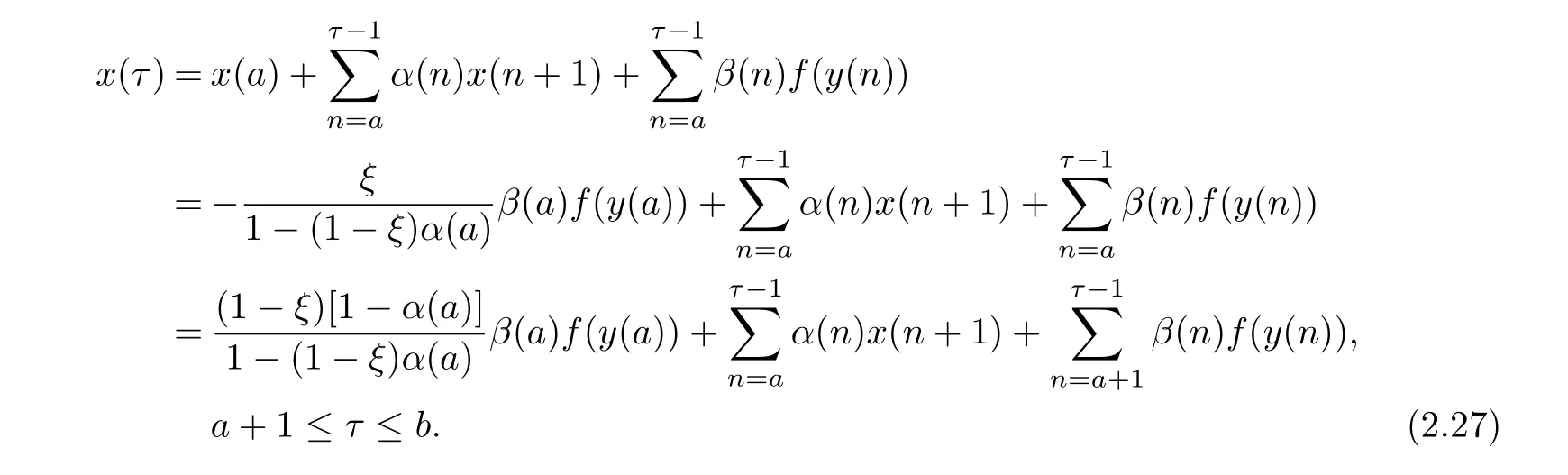
Similarly,summing the first equation of(1.1)from τ to b−1 and using(2.7)and the fact that x(b)=λ1x(a),we have

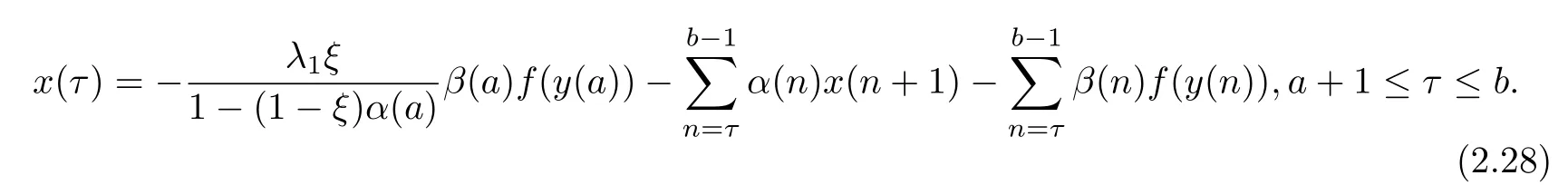
It follows from(2.27)and(2.28)that

and

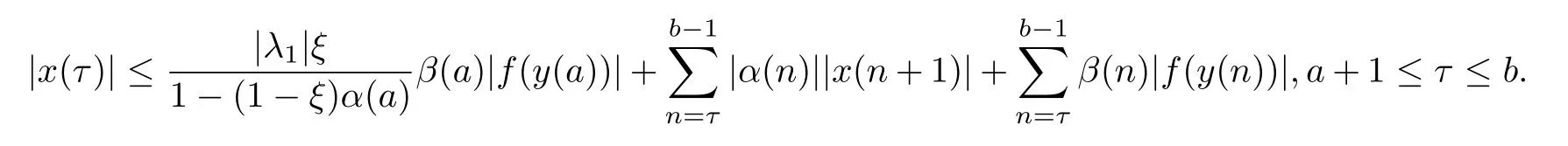
Adding the above two inequalities,we have

where

Let|x(τ∗)|=maxa+1≤n≤b|x(n)|,Applying(2.25),(2.29)and the Cauchy-Schwarz inequality,we have

Dividing the latter inequality of(2.31)by x(τ∗),we obtain

Set d=1− (1− ξ)α(a).Since(1− ξ)[1− α(a)]>0,it follows that d> ξ≥ 0,and so[d−(1− |λ1|)ξ]2≤ d[d− (1−λ1λ2)ξ].This,together with(2.26)and(2.30),implies that

Substituting this into(2.32),we obtain(2.23).The proof is completed.

Remark 2.3 Theorem 2.3 implies even if the right end-point b is not a generalized zero of x(n),we can still obtain the same result as the one of Theorem 2.1,as long as(x(b),y(b))=(λ1x(a),λ2y(a))with 0 ≤≤ λ1λ2≤ 1.

In this paper,several new Lyapunov-type inequalities are obtained for the system of nonlinear di ff erence equations(1.1).These results extend/supplement and improve some previous results in the literature.

Acknowledgements The author would like to thank the referee for his/her valuable suggestions.