The Cohomology Structures of Partial Entwining Structures
(Department of Mathematics and Statistics,Yantai 264025,China)
Abstract:In this paper we mainly reveal the rich cohomology theories for partial entwining structures.
Key words:partial entwining structure;partial entwined module;cohomology
§1. Introduction and Preliminaries
Partial group actions were introduced by R.Exel[1]in the settings of operator algebras.Recently purely algebraic view was given in[2,3,4,5].In particular,S.Caenepeel and K.Janssen introduced partial entwining structures and developed Galois theory for them.Roughly speaking,a partial entwining structure includes an algebra,a coalgebra and a map satisfying some axioms which is neither entwining structure axioms nor weak entwining structure axioms.If a partial entwining structure is at the same time a weak entwining structure,then it is an entwining structure.
Recall from[6]the author founded a cohomology theory for an entwining structure,and showed that for an entwining structure(A,C,ψ),A⊗C is a projective A-bimodule if and only if(A,M)=0 for any A-bimodules M.Also the authors in[7]generalized the results of[6]in the setting of weak entwining structures.
Our aim is to reveal that partial entwining structures also admit this cohomology theory.
Definition 1.1 Let A be a k-algebra,C a k-coalgebra,and ψ:C⊗A→A⊗C a k-map.The triple(A,C,ψ)is called a right-right partial entwining structure if the following conditions are satisfied for any a,b∈A,c∈C:
A left-left partial entwining structure is a triple(A,C,ψ),where A is a k-algebra,C a k-coalgebra,and ψ:C⊗A→A⊗C a k-map satisfying(1.3)and
Remark 1.1 A partial entwining structure(A,C,ψ)is an entwining structure if and only if
Example 1.1 Suppose H is a Hopf algebra with an idempotent e verifying∆(e)(e⊗1)=e⊗ e and ε(e)=1.Taking A:=H,C:=H and ψ :C ⊗A → A ⊗ C,c⊗ a 7→ a⊗ce,then it is easy to prove that(A,C,ψ)is a partial entwining structure.
Definition 1.2 Let(A,C,ψ)be a right-right partial entwining structure.A partial entwined module M over(A,C,ψ)is a right A-module endowed a k-map ρ :M → M⊗C,m 7→m[1]satisfying the following conditions for any m∈M,a∈A:
§2.The Cohomology Structure of A Partial Entwining Structure
In this section we will give the rich cohomology theory for partial entwining structures.
Given a right-right partial entwining structure(A,C,ψ),define σ :A⊗C → A⊗C,σ(a⊗c)=it is easy to prove that σ is a projection and/kerσ is an A-bimodule with the left action given by b•[a⊗c]=[ba⊗c]and the right action given by[a⊗c]◦b=for any a,b∈ A and c∈ C.
For any A-bimodule M and non-negative integral n,define ζn:Hom(C ⊗ An,M) →Hom(C⊗An,M), ζn(f)(c⊗a1⊗··⊗an)=f ∈ Hom(C⊗An,M),c ∈C,ai∈ A.It is easy to prove that ζnis a projection and we denote Hom(C ⊗ An,M)/kerζnby(A,M).
We define dn:(A,M)→(A,M),dn(f)(c⊗a1⊗···⊗an+1)=
Directly from the definition of partial entwining structure,it is easy to verify that dnis well-defined.Indeed,for any f∈(A,M),c∈C,ai∈A,

Lemma 2.1 dn+1dn=0.
Proof Indeed,for any c∈C,ai∈A,we have
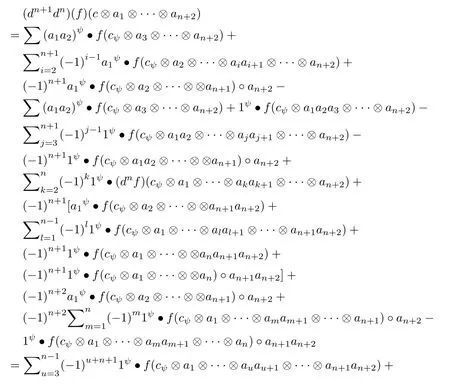

Definition 2.1 Given a right-right partial entwining structure(A,C,ψ)and an A-bimodule M.We call the cohomology of the complex Cψ(A,M)which is denoted by Hψ(A,M)a cohomology of a partial entwining structure with values in M.
Lemma 2.2 Given a right-right partial entwining structure(A,C,ψ),then the following are equivalent:
(2)The sequence of A-bimodule
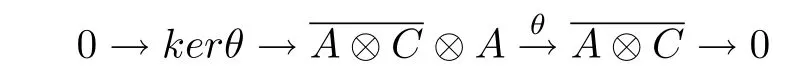
(3)There exists a 0-cocycle χ ∈(A,A⊗A)such that for any c∈C,µχ(c)=ε(c)1A,whereµdenotes the multiplication map of A.
Proof Firstly,we claim that θ is well-defined.In fact,for any a,b∈ A,c∈ C,
Obviously the first two statements are equivalent becauseis a projective A-bimodule.
Suppose(2)holds,i.e.,there exists an A-bimodule map κ:A such thatDefine
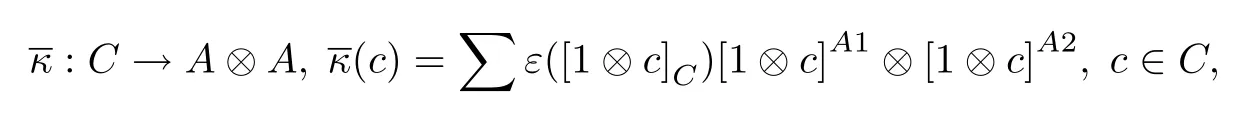
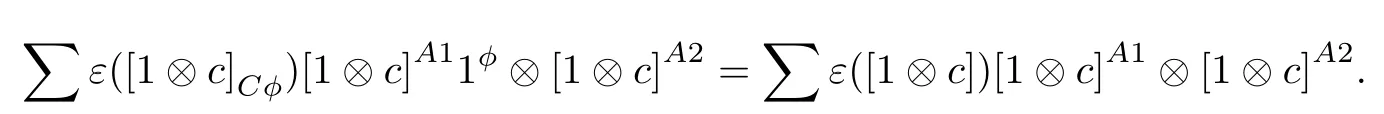
Secondly,we claim that for anyIndeed,


where we got the second equation by the fact that κ is a left A-module map and obtained the third equation by the fact that κ is a right A-module map.Hence one can immediately obtain thatis a 0-cocycle.


where we got the second equation by the equation(1.3).
Conversely,if the statement(3)holds,i.e.,there exists a 0-cocycle χ denoted by χ(c)=such thatdefine
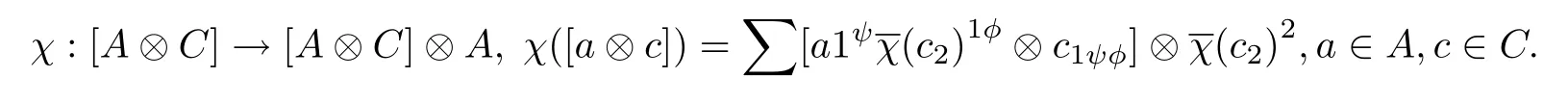
Firstly,we claim that χ is well-defined.Since for any a ∈ A and c∈ C,
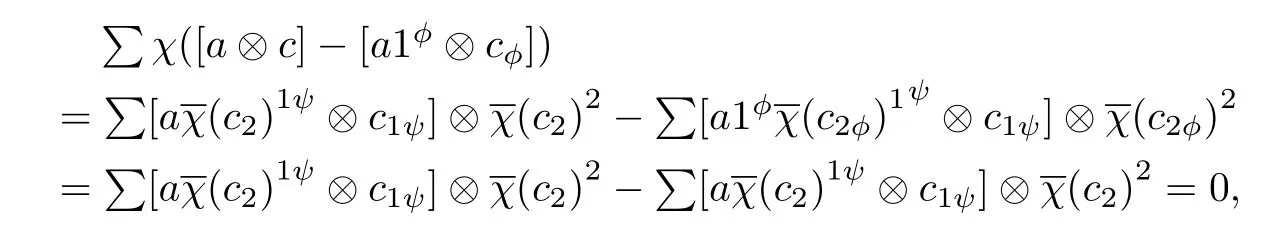
where we got the first equation by the equation(1.2)and(1.1),and used the fact thatis a 1-cocycle to obtain the second one.
Secondly,we claim that χ is an A-bimodule map.Clearly it is a left A-module map.We have to show it is also a right A-module map.Indeed,for any a,b∈A and c∈C,
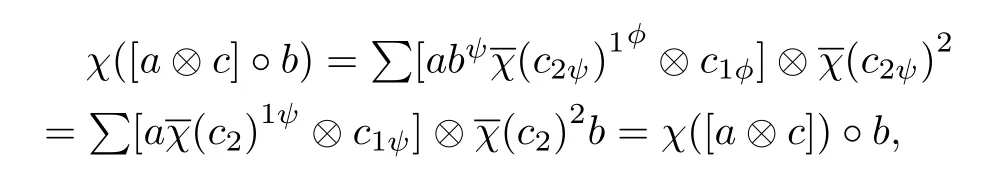
where we got the first equation by the equation(1.2)and(1.1)respectively,and used the fact thatis a 0-cocycle to obtain the second equation.
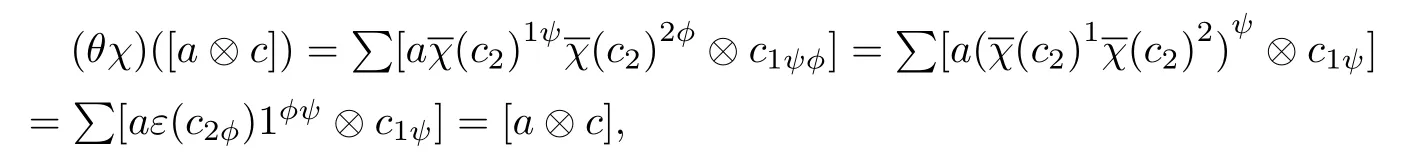
where we got the third and the last equations by the fact thatand the equation(1.2)respectively.
Lemma 2.3 Given a right-right partial entwining structure(A,C,ψ)and an A-bimodule M.Let(A,M)denote the space of n-cobundaries and(A,M)denote the space of ncocycle in(A,M),and letC,a∈A,then:
(1)The map%:AHomA(kerθ,M)→(A,M),%(f)=fDψ,f∈AHomA(kerθ,M)is a bijection;
(2)%−1((A,M))={f|kerθ|f∈AHomA(A,M)}.
Proof To prove the statement(1).We claim that%is well-defined.In fact,for any f ∈AHomA(kerθ,M),c∈ C,ai∈ A,
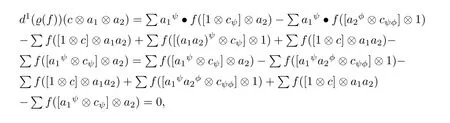
Firstly it is very easy to prove that ι is well-defined.
Secondly,we have to show that ϑ is an A-bimodule map.Clearly it is a left A-module map.It suffices to prove that it is a right A-module map.Since for any f∈Z1ψ(A,M),[a⊗c]⊗a0∈kerθ,b∈ A,
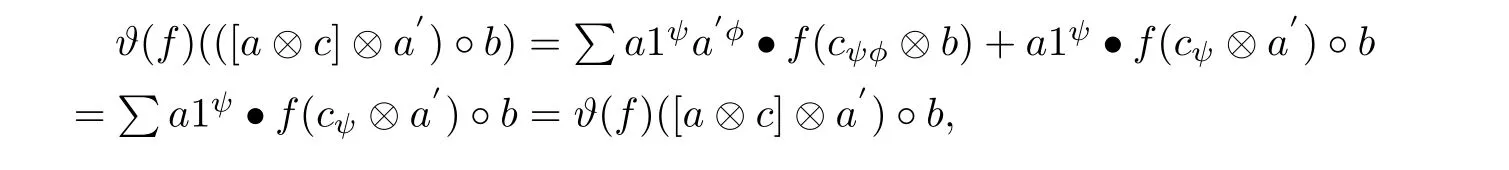
where we got the first equation by the fact that f is a 0-cocycle and used the fact that[a⊗c]⊗a0∈kerθ to obtain the third equation.
Finally,we claim that ϑ is the inverse of%.On one hand,for any f∈(A,M),c∈C,a∈A,we can obtain that=0 since f∈(A,M),
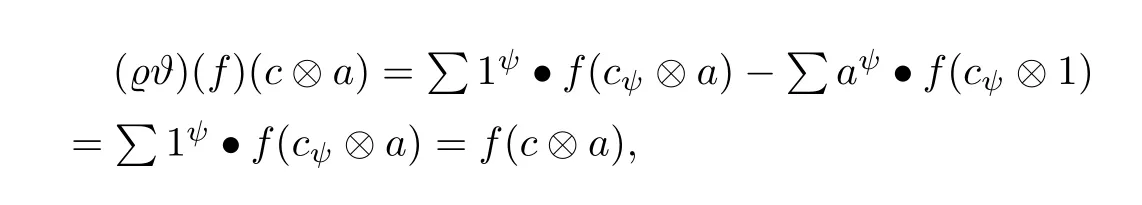
where we got the last equation by the definition of(A,M).
On the other hand,for any f ∈AHomA(kerθ,M)and[a⊗c]⊗a0∈ kerθ,

where we got the second equation by the fact that[a⊗c]⊗a0∈ kerθ.
To prove the statement(2).Suppose thatfor some f∈then for any
By straightforward computation we also verify that
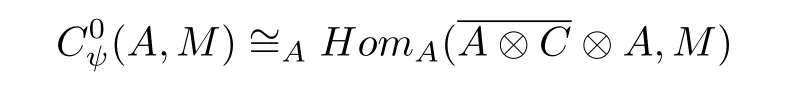

Therefore we complete the proof.
After these preparation,we now can give our main result.
Theorem 2.1 For any right-right partial entwining structure(A,C,ψ),is a projective A-bimodule if and only if(A,M)=0 for any A-bimodule M.
As an example we compute the partial entwining structure associated to a partial coalgebra-Galois extension.
Let(A,C,ψ)be a partial entwining structure such that A ∈(ψ)with the coaction defined bywhere g is a grouplike-element of C,and let T=AcoC={b∈ A|is a left A-linear and right C-colinear isomorphism then we say that A is a partial coalgebra-Galois extension of T.
Proposition 2.1 Let(A,C,ψ)be a partial entwining structure associated with a partial coalgebra-Galois extension as mentioned.Then(A,M)=MT={m∈M|b•m=m◦b,for all b∈T}.
Proof Denote the inverse of can by can−1and can−1(1⊗c)=for all c∈ C.Clearly for all a∈ A,=1⊗a,and so by the fact that A ∈(ψ)one canfor all a,a0∈ A.In particular,for all b ∈ T,For any a ∈ A,c∈ C,we have[cancan−1([1⊗c])]◦a=[1⊗ c]◦a,that is

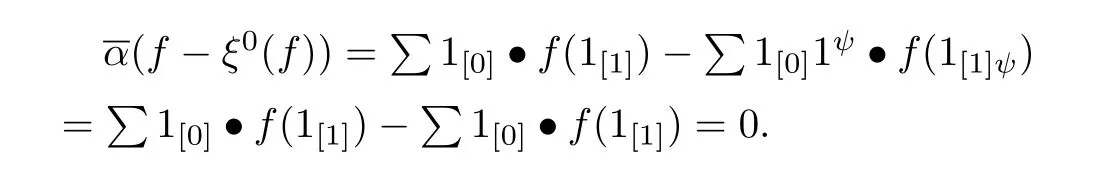
Since f is a 0-cocycle,we can obtain for all b∈T,
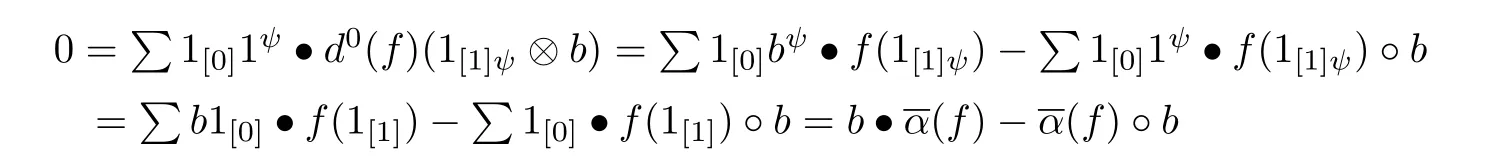
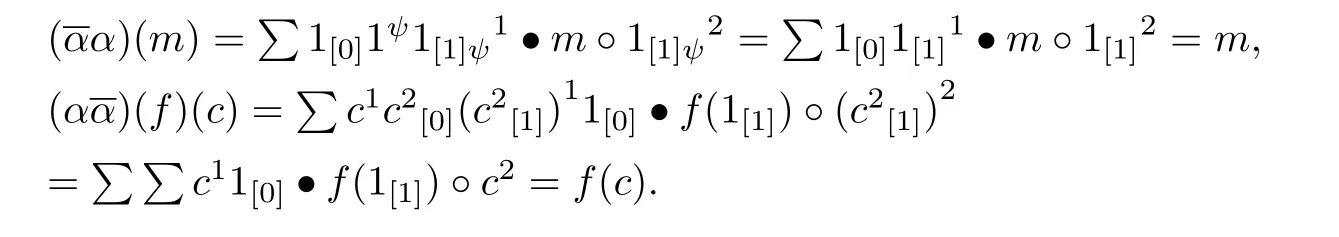
 Chinese Quarterly Journal of Mathematics2019年1期
Chinese Quarterly Journal of Mathematics2019年1期
- Chinese Quarterly Journal of Mathematics的其它文章
- A Remark on Double Ore Extensions
- Lyapunov-type Inequalities For A System of Nonlinear Di ff erence Equations
- Analysis On an SEIRS Epidemic Model with Pulse Vaccination and Two Time Delays
- Study On the Impact of Open Residential Block on Urban Traffic Congestion Based on Dynamic Com-prehensive Evaluation Model
- Some Results on H-cordial Graphs and Semi-H-cordial Graphs
- An Improvement in Ordered Cone b-metric Spaces Over Banach Algebras
