The Properties of The Rational Maps With Buried Components
(Department of Mathematics and Physics,Beijing Institute of Petrochemical Technology,Beijing 102617,China)
Abstract:Let R(z)be an NCP map with buried components of degree d=degf≥2 on the complex sphereand HD denotes the Hausdor ffdimension.In this paper we prove that if Rn→R algebraically,and Rnand R topologically conjugate for all n>>0,then Rn is an NCP map with buried components for all n>>0,and for some C>0,
Key words:Julia set;Buried components;Net;Hausdor ffdimension
§1. Introduction
Let R(z)be a rational map of degree d=degR≥2 on the complex sphereThe Julia set J(R)of a rational function R is defined to be the closure of all repelling periodic points of R,its complement set is called Fatou set F(R).It is known that J(R)is a perfect set(so J(R)is uncountable,and no point of J(R)is isolated),and also that if J(R)is disconnected,then it has infinitely many components.

for every x∈X and Rnis topologically conjugate to a subshift of finite type.If only condition|(Rn)0(x)|>1 is satisfied we call the map R|Xexpanding.
We call a rational function R:J(R)7→ J(R)hyperbolic if there exists n ≥ 1 such that

Denote CV(R)the critical values of a rational function R.Let

It follows from[1,Theorem 2.1]that a rational function R:J(R)7→J(R)is hyperbolic if and only if
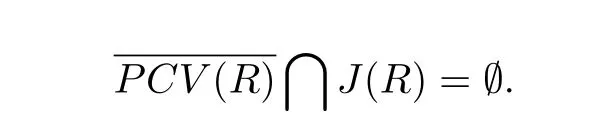
Denote by J(R)the Julia set of a rational function.A rational map R is expansive if the Julia set J(R)contains no critical points of R.It follows from[1]that each hyperbolic rational function is expansive and that a rational function is expansive but not hyperbolic if and only if the Julia set contains no critical points of R but intersect the ω-limit set of critical points.
We call expansive but not hyperbolic rational functions parabolic.It follows from[1]that a rational function R:J(R)7→J(R)is expansive but not hyperbolic if and only if the Julia set J(R)contains no critical points of R but contains at least one parabolic point.
We recall that if T:X→X is a continuous map of a topological space X,then for every point x ∈ X,the ω-limit set of x denoted by ω(x)is defined to be the set of all limit points of the sequence{Tn(x)}n≥0.We call a point x recurrent if x ∈ ω(x);otherwise x is called non-recurrent.
The class of NCP maps obviously contains all expanding and parabolic maps.It also comprises the important class of so called subexpanding maps which are defined by the requirement that R|ω(Crit(R))∩J(R)is expanding and the class of geometrically finite maps defined by the property that the forward trajectory of each critical point contained in the Julia set is finite and disjoint from ω-limit set;see ref.[2].
In paper[3],Sullivan pointed out that there is a surprising good dictionary connecting complex iteration theory and Kleinian groups.He proves that there exists a Kleinian group such that the limit set contains some points not lying on the boundary of any component of the set of discontinuity,and the set of these points is called residual limit set.By analogy with this concept,we define a buried point to be a point on the Julia set not lying on the boundary of any Fatou component.A buried component is defined to be a component of the Julia set which is not on the boundary of any Fatou component.
By paper[4]we have the following results.
Theorem A[4]If J(R)is disconnected,then it has uncountable many components,and each point of J(R)is an accumulation point of distinct components of J(R).
Theorem B[4]Suppose that J(R)is disconnected,and that every component of F(R)has finite connectivity.Then J(R)has a buried component.
In paper[5]Qiao proved the following result.
Theorem C[5]Let R(z)be a rational map of degree larger than 1,J(R)6=Then J(R)contains buried components if and only if J(R)is disconnected and F(R)has no completely invariant component.
McMullen,Beardon and Qiao give some examples in which J(R)has a buried component(see refs.[4-6]).
A rational function R(z)can be expressed as the quotient
of two polynomials,where p(z)and q(z)have no common roots.The degree d=degR of R=p/q is then equal to the maximum of the degree of p and q.Thus we can let

where pn(z)and qn(z)have no common roots,and set dist(Rn,R)=max{|an0−a0|,|an1−a1|,···,|anp− ap|,|bn0− b0|,|bn1−b1|,···,|bnq−bq|}.
We say rational maps Rnconverge to R algebraically if degRn=degR and,when Rnis expressed as the quotient of two polynomials,the coefficients can be chosen to converge to those of R.Equivalently,Rn→R uniformly in the spherical metric.
The Julia set J(R)is compact,and the buried components are connected subsets of J(R).So we have the buried components Jb(R)are also compact.
n>>0 means for all n sufficiently large,and HD(A)denotes the Hausdor ffdimension of a set A.In this paper we shall prove the following theorems:
Theorem 1 Let R be an NCP map with buried components.If Rn→R algebraically,and Rnand R topologically conjugate,that is,there exists a homeomorphism h:J(Rn)→J(R)such that h◦Rn=R◦h for all n>>0,then Rnis an NCP map with buried components for all n>>0,and for some C>0,
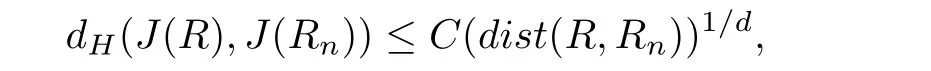
where dHdenotes the Hausdor ffdistance,and
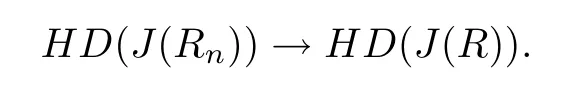
Let(X,ρ)be a metric space,the space X is openly locally connected at the point x ∈ X if there exists arbitrary small connected open neighborhood of x in X.The space X is locally connected if X is openly locally connected at every point.
Theorem 2 Let R(z)be an NCP map with buried components,if J(R)is locally connected,then any component Ji(R)is either a real-analytic curve or HD(Ji(R))>1.
§2. Preliminaries and the Construction of A Net
Let X be a connected complex manifold.A holomorphic family of rational maps,parameterized by X,is a holomorphic map R:X×We denote this map by Rλ(z),where λ∈X and z∈then Rλ:is a rational map.
Let x be a basepoint in X.A holomorphic motion of a setparameterized by(X,x)is a family of injections

one for each λ in X,such that φλ(e)is a holomorphic function of λ for each fixed e,and φx=id.
Definition 2.1 Given a holomorphic family of rational maps Rλ,we say the corresponding Julia sets J(Rλ)⊂move holomorphically if there is a holomorphic motion
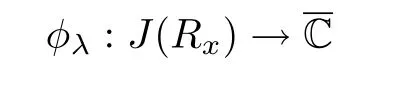
such that φλ(J(Rx))=J(Rλ)and
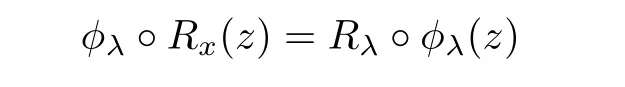
for all z in J(Rx).Thus φλprovides a conjugacy between Rxand Rλon their respective Julia sets.The motion φλis unique if it exists,by density of periodic cycles in J(Rx).
The Julia sets move holomorphically at x if they move holomorphically on some neighborhood U of x in X.
A periodic point z of Rxof period n is persistently indi ff erent if there is a neighborhood U of x and a holomorphic map W:U→such that W(§)= ‡,(W(λ))=W(λ),and|()0(W(λ))|=∞for all λ in U.(Here()0(z)=/dz.)
Lemma 2.1[7](Characterizations of stability) Let Rλbe a holomorphic family of rational maps parameterized by X,and let x be a point in X.Then the following conditions are equivalent:
1.The number of attracting cycles of Rλis locally constant at x.
2.The maximum period of an attracting cycle of Rλis locally bounded at x.
3.The Julia set moves holomorphically at x.
4.For all y sufficiently closed to x,every periodic point of Ryis attracting,repelling or persistently indi ff erent.
5.The Julia set Jλdepends continuously on λ (in the Hausdor fftopology)on a neighborhood of x.
Suppose in addition that ci:X→are holomorphic maps parameterizing the critical points of Rλ.Then the following conditions are also equivalent to those above:
6.For each i,the function λ 7→(ci(λ)),n=0,1,2,···form a normal family at x.
7.There is a neighborhood U of x such that for all λ in U,ci(λ) ∈ Jλif and only if ci(x)∈Jx.
The definition of conformal measures for rational maps was first given by Sullivan as a modification of the Patterson measures for limit sets of Fuchsian groups.A more general definition,showing the connection to ergodic theory,has been given by M.Denker and M.Urba´nski earlier.Let t≥0,a probability measure m on J(R)is called t-conformal for R:J(R)→J(R)if m(J(R))=1 and
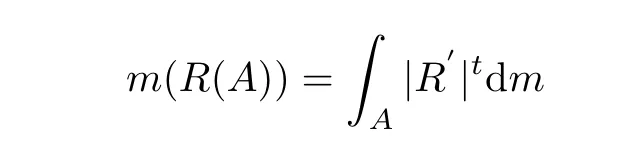
for every Borel set A⊂J(R)such that R|Ais injective.
Let R be an NCP map.Denote by Λ(R)the set of all parabolic periodic points of R(these points belong to the Julia set and have an essential influence on its fractal structure),and Crit(R)of all critical points of R.We put

Set
Definition 2.2 We define the conical set Jc(R)of R as follow.First,say x belongs to Jc(R,r)if for any†>0,there is a neighborhood U of x and n>0 such that diam(U)<ε and
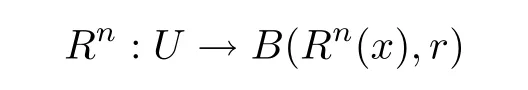
is a homeomorphism.Then set
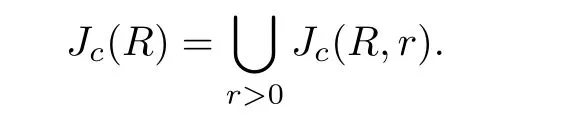
We have x∈Jc(R)if and only if arbitrary small neighborhood of x can be blow up univalently by the dynamics to balls of definite size centered at Rn(x).
Lemma 2.2[8]If R:J(R)→J(R)is an NCP map,then

Note that Curtis T.McMullen used the term radial Julia set Jrad(R)instead of conical set Jc(R)in analogy with Kleinian groups;see ref.[9].
By paper[9],we have the set Sing(R)is countable.
Let 0<λ<1.Then there exist an integer m≥1,C>0,an open topological disk U containing no critical values of R up to order m and analytic inverse branches:U→of Rmn(i=1,···,kn≤ dnm,n ≥ 0),satisfying:
(1) ∀n ≥ 0,∀1≤ i≤ kn+1,∃1≤ j≤ kn,Rm◦=,
(3) for each fixed n ≥ 1,for all i=1,···,knthe setsare pairwise disjoint and⊂U.
Now we states as a lemma the following consequence of(1)-(3)by the definition 2.2.
Lemma 2.3 Let R(z)be an NCP map.For each n,letℵn=S{(U):j=1,···,kn}and letS,where U is an open topological disk containing no critical values of R.Thenℵis a net of Jc(R),i.e.any two sets inℵare either disjoint or one is a subset of the other.
Consider the netℵ,given by Lemma 2.3.For n≥ 0,the preimages of the setsℵiunder Rnthat intersect J(R)are called the nth step pieces of the net.Note that for n≥1 the collection of all the nth step pieces also is a net;we call it a refinement of the netℵ.
Lemma 2.4 Let R(z)be an NCP map,and W be an nth step piece of the netℵi,then the inverse of
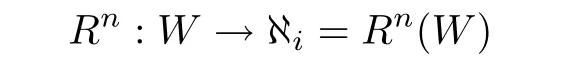
extends in a injective way to a neighborhood ofonly depending on i.
Proof Refining the net if necessary,we will prove that for some m≥1 all the mth step pieces(or some of the mth step pieces)of the net are compactly contained in someℵi.Then the net formed by the mth step pieces will be the desired net.Thus it is enough to prove that the diameters of the mth step pieces of the net converge uniformly to zero as m→∞.
Let ε>0,and N ≥ 1 be such that we can partition each ℵiin at most N connected sets of diameter less than ε>0.If necessary we can refine the disks ℵismall enough,then R is injective in each cover of the net.Let W be an mth step piece of the net,so that Rmis injective in W.Then by the property(2)of net we have diam(W)→0 as m→∞.The proof of this lemma is complete.
As in immediate consequence,together with the Koebe Distortion Theorem,we obtain the Bounded Distortion Property.
Lemma 2.5(Bounded Distortion Property) For any k≥0 the distortion of Rkin each of the kth step pieces of the net is bounded by some constant K>1,independent of k.
§3. Conformal Iterated Function System
Let I be a countable index set with at least two elements and let S={φi:X →X:i∈I}be a collection of injective contractions from a compact metric space X(equipped with a metric ρ)into X for which there exists 0 is a singleton therefor,denoting its only element by π(τ),defines the coding map The main object in the theory of iterated function systems is the limit set defined as follows. Observe that Γ satisfied the natural invariance equality,Γ = ∪i∈Iφi(Γ).Let S(∞)be the set of limit points of all sequences xi∈ φi(X),i∈ I0,where I0ranges over all infinite subsets of I;see ref.[10]. Lemma 3.1[11]Iflimi∈Idiam(φi(X))=0,then(S(∞)). An iterated function system S={φi:X → X:i∈I},is said to be conformal if X ⊂ Rdfor some d≥1 and the following conditions are satisfied. (a)Open Set Condition(OSC).φi(IntX)∩φj(IntX)=∅for every pair i,j∈I,i 6=j. (c)There exists an open connected set V such that X⊂V⊂Rdsuch that all maps φi,i∈ I,extend to C∞conformal di ff eomorphisms of V into V.(Note that for d=1 this just means that all the maps φi,i ∈ I,are monotone di ff eomorphism,for d=2 the words conformal mean holomorphic and antiholomorphic,and for d=3,the maps φi,i ∈ I are M¨obius transformations.) (d)(Cone Condition)There exist α,l>0 such that for every x ∈ ∂X there exists an open cone Con(x,u,α)⊂ Int(V)with vertex x,the symmetry axis determined by vector u of length l and a central angle of Lebesgue measure α.Here Con(x,u,α)={y:0<(y − x,u) ≤cosα||y−x||≤ l}. (e)Bounded Distortion Property(BDP).There exists K≥1 such that for every ω ∈ I∗and every pair of points x,y ∈ V,wheremeans the norm of the derivative. Lemma 3.2 If R is an NCP map and J(R)is locally connected,then Jc(R)admits a conformal iterated function system satisfying the conditions(a)-(e). ProofLet R be an NCP map.By Lemma 2.2,Jc(R)admits a net such that Bi∩Bj= ∅,i 6=j.Moreover,we may require the existence of an integer q ≥ 1 and σ >0 such that the following holds: If x∈Jc(R),say x∈Bi,and Rqn(x)∈Bt,then there exists a unique holomorphic inverse branch:U(Bt,2σ) →of Rqnsending Rqn(x)to x.Moreover⊂Biand,taking q sufficiently large,we have R−qn x(U(Bt,σ/2))⊂ Int(Bi), for sufficiently small σ,then, For every t=1,2,...,n,...,we now build recursively our iterated function system Stas a disjoint union of the families,j≥ 1,as follows.consists of all the maps,where x,Rq(x)∈ Jc(R)∩Bt.S2tconsists of all the maps,where x,R2q(x)∈ Jc(R)∩Btand Rq(x)/∈Bt.Suppose that the families,...,have been already constructed.Thenis composed of all the mapssuch that y,Rqn(y)∈Jc(R)∩Btand Rqj(y)∈/Btfor every 1≤j≤n−1. Let V⊃Jc(R)be an open set constructed by the net such that it disjoints from the parabolic and critical points and their inverse orbits of R.For any x∈V and finite n<∞,we have then where x,y∈V and 1≤K<∞is a constant.So the condition(e)Bounded Distortion Property(BDP)holds.It is evident that Rnis holomorphic and antiholomorphic of V into V for all n≥1,then the condition(c)holds.Since J(R)is locally connected,and condition(d)is satisfied.Condition(b)follows immediately from(3.1).In order to prove condition(a),take two distinct mapsandbelong to St.Without loosing generality we may assume that m≤n.Suppose on the contrary that Then Lemma 4.1[9]If Rn→R algebraically,then J(R)⊂liminf J(Rn). Proof of Theorem 1 Step 1 Since for any non constant rational map R,and any positive integer p,J(Rp)=J(R),we can replace Rn→R with→Rp(which does not change the Julia set).Rnand R topologically conjugate,that is,there exists a homeomorphism h:J(Rn)→J(R)such that for all n>>0.If Rnis not an NCP map for all n>>0,then J(Rn)contains a dense subset Θ⊂J(Rn)such that for all n>>0.This contradiction prove that Rnis an NCP map for all n>>0. Since Rn→R algebraically,we have if Rnand R are expressed as the quotient of two polynomials,the coefficients of Rncan converge to those of R.Let λR={ai,i=0,1,···,p;bj,j=0,1,...,q}and λRn={ani,i=0,1,···,p;bnj,j=0,1,...,q}be the coefficients of the maps R(z)and Rn(z)respectively,and If Rn→R algebraically,we have Since Rnand R topologically conjugate,that is,there exists a homeomorphism h:J(Rn)→J(R)such that for all n>>0,we have the Julia set moves holomorphically by the definition 2.1.It follows by lemma 2.1(Characterizations of stability)that the Julia set moves holomorphically at λR,and there is a unique holomorphic motion such that φλRn(J(R))=J(Rn)and for all z in J(R). Since the holomorphic motion φλRnis a holomorphic function of λRnin a neighborhood of λR,and φλR=id.We have for all z in J(R).By item 5 in Lemma 2.1,the Julia set J(R)depends continuously on λR(in the Hausdor fftopology)on a neighborhood.So we have where some constant C>0 only depending on R. Let∀z∈ J(R)and w= φλRn(z)∈ J(Rn),and Uzbe the nets containing z.Denote by Vzthe pull-back of Uzto∈J(R)by Rlfor l≥ 1,where=R−l(z).It follows by the Lemma 2.3 and considering that the Uzare nets that if Vzis a pull-back of Uz,then either Vz∩Uz=∅or Vz⊂Uz.If w∈Uz,then it follows by(4.1)and(4.2)that where A∼B means C−1B So we obtain for some constant C>0 only depending on R,where dHdenotes the Hausdor ffdistance. Step 2 Let h=HD(J(R))be the Hausdor ffdimension of the Julia set J(R)of the NCP map R.It follows by[1]that there exists exactly one h-conformal measureµand this measure is atomless(theµmeasure of a point is zero).The unique h-conformal measure for R:J(R)→J(R)supported on J(R)has exponent h=HD(J(R)).For all n>>0,Rnis an NCP map.The unique hn-conformal probability measureµnfor Rn:J(Rn)→ J(Rn)supported on J(Rn)has exponent hn=HD(J(Rn))and it is atomless;see ref.[1].Thus to prove that it is enough to prove that there is a neighborhood Br(b)of the critical point b∈J(R)such that Since R is an NCP map,there exists l>1 such that Rl(b)=w ∈ ω(b),where the set ω(b)(⊂ Sing(R))of accumulation points of the orbit of the critical b.By the completely invariant property of the Julia set,it is enough that we only prove the following In fact any weak accumulation point ν ofµngives an R-invariant measure for R:J(R)→ J(R).The previous limit implies thatµn→µ=ν,and it follows that hn→h.Hence,we obtain that Since R is an NCP map,we consider the netℵas in lemma 2.3 and consider constants C0>0 and θ0∈ (0,1).Let w ∈ ω(b)⊂ Sing(R)be any point.Since Rn→ R algebraic convergence,and Rnand R topologically conjugate,we have for all m≥1 and n>>0.Moreover we may suppose that there is a uniform Bounded Distortion property:There is a constant K>1 so that for every k≥1 and every kth step piece W of the netℵi,the distortion ofin W is bounded by K for all n>>0;see lemma 2.5. Let w∈ω(b)be any point and Bqbe the qth step piece containing uw=Rl(w)and Vqbe the pull-back of Bqby Rlcontaining w.Since Rn→R algebraically and dH(J(Rn),J(R))≤C(dist(Rn,R))1/d,we letbe the pull-back of Bqbycontaining w,n>>0.It follows that for r>0 small there is q=q(r)→∞,as r→0 so that Br(w)⊂for all n>>0.So we only need to prove that Let D be a disc containing w,small enough so thatis at most of degree d.Refining the net if necessary,suppose that B1⊂Since the probability measureµnis atomless for all n>>0,we have Note that for m≥1 we have By formula(4.3),we have for all n>>0 and some constant C1.By the uniform Bounded Distortion Property and considering thatµnis a probability measure,for some constant C2we have for all w∈Bm.So Since we conclude that Therefor,we get Step 3 Since Rn→R algebraically,and we get J(Rn)is disconnected for all n>>0.By Theorem C,we only need to prove F(Rn)has no completely invariant component for all n>>0.Indeed,supposing that F(Rn)has a completely invariant component F0(Rn)for n>>0(i.e.Rn(F0(Rn))=F0(Rn)=(F0(Rn))).Since Rn→R algebraically,by Lemma 4.1,we get for all n>>0.There exists some F0(R)such that F0(R)⊃F0(Rn)for all n>>0,then R(F0(Rn))=R((F0(Rn)))and R−1(F0(Rn))=R−1(Rn(F0(Rn))).Since Rn→ R algebraically and Rnand R topologically conjugate for all n>>0,we have dH(J(Rn),J(R))≤C(dist(Rn,R))1/d.Equivalently, specially,dH(F0(Rn),F0(R))≤C(dist(Rn,R))1/d→0.So we obtain and It follows that F0(R)is a completely invariant component of R,and this contradict to Theorem C.The proof of Theorem 1 is finished. Given x∈ C,θ,r>0,we put where η is a representative of θ.We recall that a set Y has a tangent in the direction θ at a point x∈Y if for every r>0 where H1denotes the 1-dimensional Hausdor ffmeasure(see refs[12,13]).Following[12]we say that a set Y has a strong tangent in the direction θ at a point x provided for each 0< β ≤ 1 there is a some r>0 such that Y ∩ B(x,r)⊂ Con(x,θ,β). Lemma 4.2[13]If Y is locally arcwise connected at a point x and Y has a tangent θ at x,then Y has strong tangent θ at x. We call a point τ∈ I∞transitive if ω(τ)=I∞,where ω(τ)is the ω-limit set of τ under the shift transformation σ :I∞→ I∞.We denote the set of these points byand put Γt=π().We call the Γtthe set of transitive points of ΓStand notice that for every τ∈,the set{π(σnτ):n ≥ 0}is dense in ΓStorΓSt. Lemma 4.3[13]Ifhas a strong tangent at a point x= π(τ),τ∈ I∞,thenhas a strong tangent at every point If R is an NCP map,by Lemma 2.3 and Lemma 3.2,Jc(R)admits a conformal iterated function system St.It is obvious that the Julia set J(R)coincides with the limit setby Lemma 3.1.So we have, Lemma 4.4 If R is an NCP map and the Julia set J(R)is locally connected,then J(R)has a strong tangent at every point of J(R). Proof of Theorem 2 Since R is an NCP map with a buried component,the Julia set J(R)is disconnected and it has uncountable many components by Theorem A and Theorem C.Denoted by Ji(R)any component of J(R),if HD(Ji(R))=1,then our goal is to show that Ji(R)is a real-analytic curve. J(R)is locally connected,then Jc(R)admits a conformal iterated function system St={:t∈s}for finite s satisfying the conditions(a)-(e)by Lemma 3.2. Let w∈Ji(R)be a repelling fixed point and l be the straight line determined by the strongly tangent direction of Ji(R)at w.(If Ji(R)is a real-analytic curve,then there exists a conformal map ψ :D → H such that ψ(w)=w and ψ(∂D)is the straight line determined by the strongly tangent direction of Ji(R)at w,where∂D⊃Ji(R)and H is the half plane.So we can suppose that Ji(R)is a segment of a straight line.)Then w is an attracting fixed point of R−1.Moreover, is a conformal map,where U(w)is a disk centered at w.Suppose now that Ji(R)is not contained in l.Consider x∈Ji(R)l such that x∈U(w),then and for every n≥0 we have Since the map R−1:U(w)→ U(w)is conformal,we get It follows that w and R−n(x)(n≥ 0)are contained in the same line l06=l and this implies that l0is the strongly tangent straight line of Ji(R)at w.Therefor,we conclude that l is not a strongly tangent straight line of Ji(R)at w.This contradiction proves that Ji(R)⊂l.So Ji(R)is a real-analytic curve.
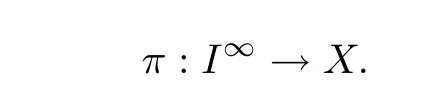

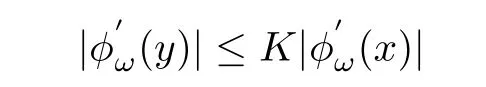

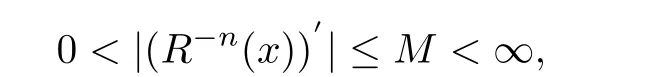
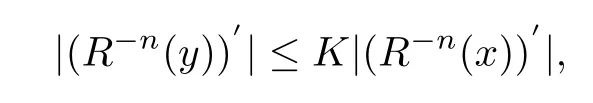
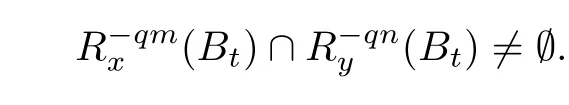
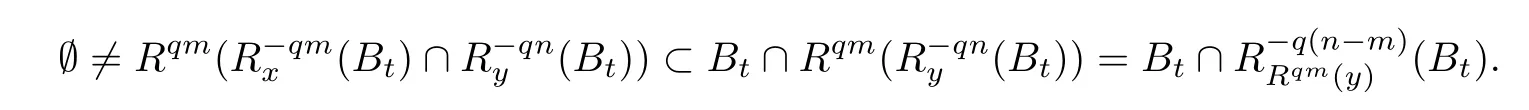
§4. Proof of The Main Results
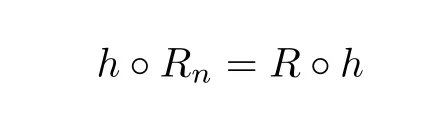
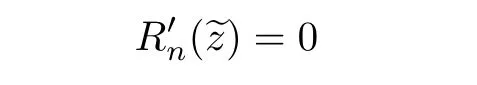
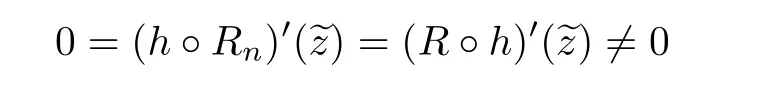
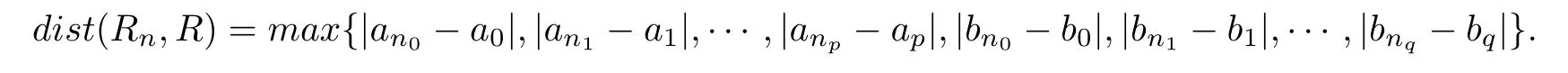
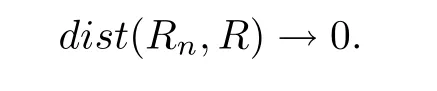
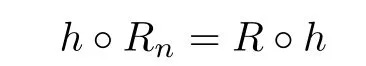
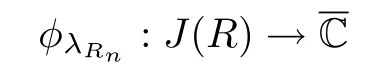

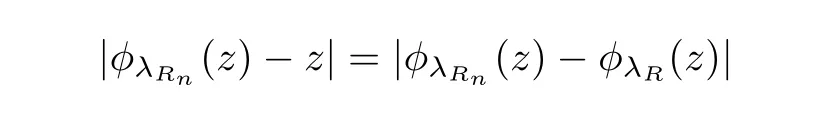
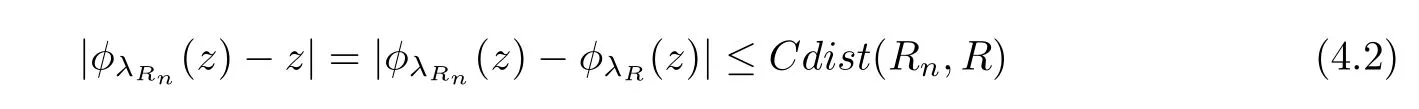
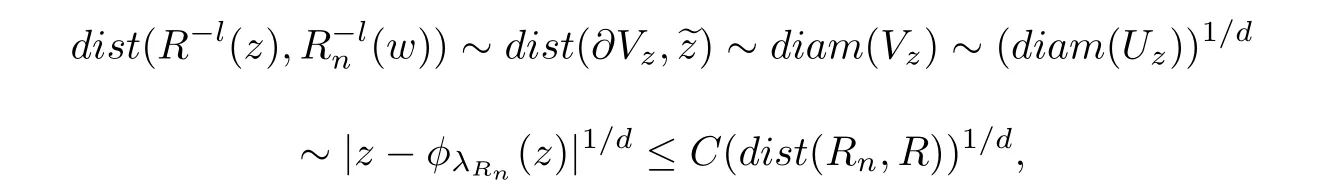

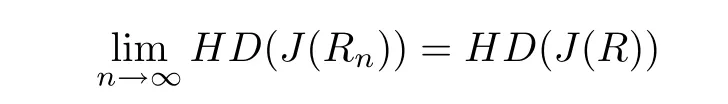
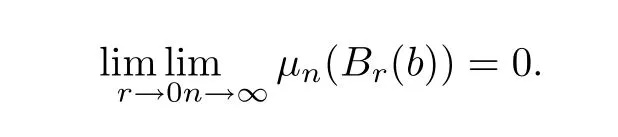

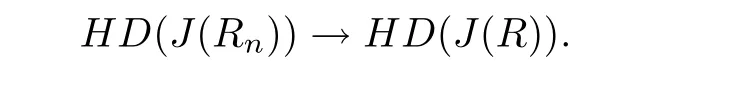
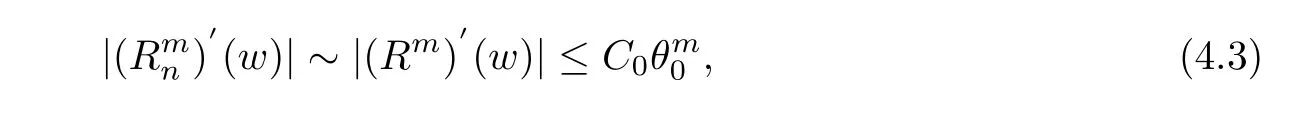
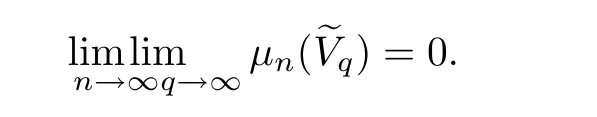

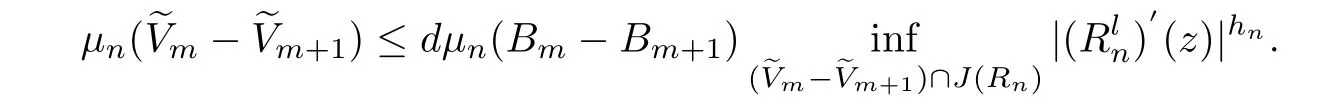

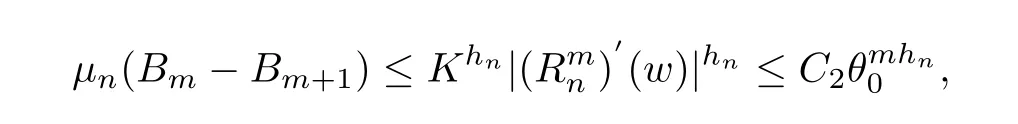
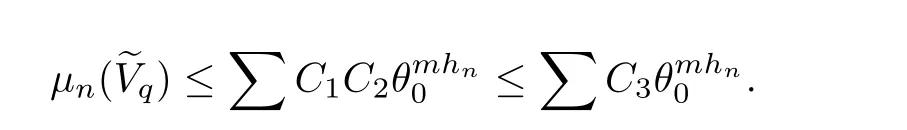

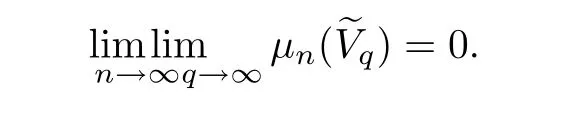
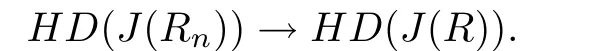
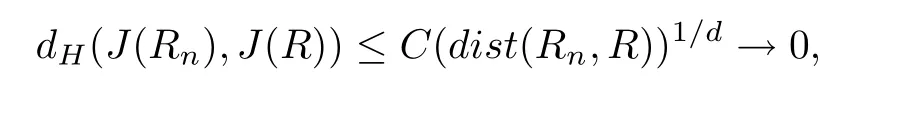

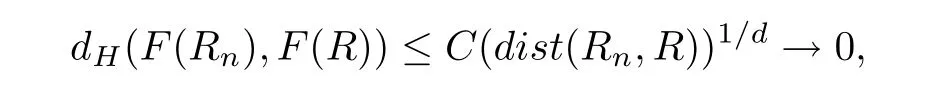

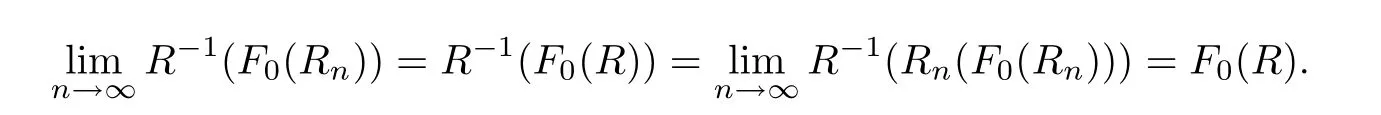
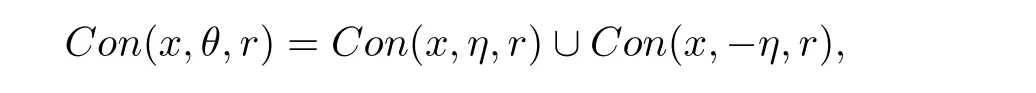

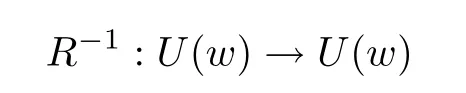

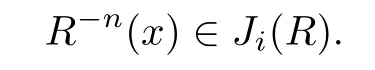
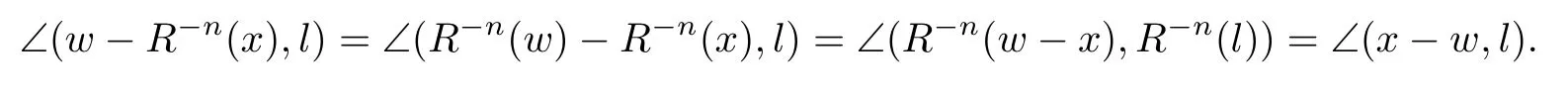
 Chinese Quarterly Journal of Mathematics2019年1期
Chinese Quarterly Journal of Mathematics2019年1期
- Chinese Quarterly Journal of Mathematics的其它文章
- A Remark on Double Ore Extensions
- Lyapunov-type Inequalities For A System of Nonlinear Di ff erence Equations
- Analysis On an SEIRS Epidemic Model with Pulse Vaccination and Two Time Delays
- The Cohomology Structures of Partial Entwining Structures
- Study On the Impact of Open Residential Block on Urban Traffic Congestion Based on Dynamic Com-prehensive Evaluation Model
- Some Results on H-cordial Graphs and Semi-H-cordial Graphs
