When Exchange Rings are Von Neumann Regular

(College of Mathematics and Computer Science,Hanjiang Normal Universtiy,Shiyan 442000,China)

Abstract:We study when exchange rings are von Neumann regular.An exchange ring R with primitive factors Artinian is von Neumann regular,if the Jacobson radical of any indecomposable homomorphic image of R is T-nilpotent,and if any indecomposable homomorphic image of R is semiprime.Every indecomposable semiprimitive factor ring of R is regular,if R is an exchange ring such that every left primitive factor ring of R is a ring of index at most n and if R has nil-property.

Key words:exchange ring;von Neumann regular ring;strong π-regular ring

§Introduction

In this paper,J(R)denotes the Jacobson radical of a ring R.All modules are left R-modules.Regular always means von Neumann regular.

Let R be an associative ring with identity,and M a unitary left R-module.Crawley and Jonsson called M to have the exchange property if for every left R-module A and any two decompositions of A,

where M0∼=M,there are submodules⊆ Aisuch that

It follows from the modular law thatmust be a direct summand of Aifor all i.Warfield[13]called a ring R an exchange ring if R has the exchange property as a left R-module.He proved that this definition is left and right symmetric.Many classes of rings are contained in this class of rings,for instance,we have the following relations:local rings are semiperfect rings,semiperfect rings are semiregular rings,and semiregular rings are exchange rings.Von Neumann regular rings are π-regular rings,π-regular rings are exchange rings.Artinian rings are perfect rings,perfect rings are strong π-regular rings,strong π-regular rings are strongly clean rings,strongly clean rings are clean rings,clean rings are exchange rings,see[3-6,9-15].

Many authors have studied exchange rings with primitive factors Artinian.It was proved by Yu that an exchange ring with primitive factors Artinian is semi-strongly π-regular,if R/J(R)is homomorphically semiprimitive(i.e.,every ring homomorphic image of R/J(R)has zero Jacobson radical)[15,Theorem 3.6].In[6,Theorem 8],it was proved that the exchange ring R with primitive factors Artinian is a strongly π-regular ring,if the Jacobson radical of any homomorphic image of R is either T-nilpotent or locally nilpotent.It follows from Wu[14,Proposition 2.8(1)]wt that an exchange ring R with primitive factors Artinian is regular if R is homomorphically semiprimitive.It was also proved by Wu in[14,Proposition 2.8(2)]wt that for an exchange ring R with primitive factors Artinian,R is a von Neumann regular ring if every right primitive factor ring of R is flat as a left R-module.In Section 1,we prove that an exchange ring R with primitive factors Artinian is von Neumann regular,if the Jacobson radical of any indecomposable homomorphic image of R is right T-nilpotent,and if any indecomposable homomorphic image of R is semiprime.We also give some applications.

Recall that a ring R is called left weakly P-exchange ring if every left projective module over R has the finite exchange property.We call a ring R to be of bounded index or be of index at most n if there exists a number n such that rn=0 for every nilpotent element r of R.A ring R is called an I0-ring if every left ideal of R that is not contained in J(R)contains a nonzero idempotent.This property is left and right symmetric[12,Lemma 15.1].It is well-known that R is a strongly π-regular ring and any prime factor ring of R is isomorphic to the ring of n × n matrices over a division ring,if R is a weakly P-exchange ring of bounded index,where n≤k if R has bounded index k[11,Theorem 4.11].Recall that a ring without nonzero nilpotent ideals is called a semiprime ring,and a ring is called a prime ring if the product of any two of its nonzero ideals is not equal to zero.It is clear that the prime ring is semiprime.The intersection of all prime ideals of a ring R is called the prime radical of R.In Section 3,we prove that every indecomposable semiprimitive factor ring of R is von Neumann regular,if R is an exchange ring such that every left primitive factor ring of R is a ring of index at most n and R has nil-property.

§1. Exchange Rings with Primitive Factors Artinian

It is well-known that a ring R is von Neumann regular if and only if the following conditions hold:R is a semiprime ring,every prime factor ring of R is a regular ring,and the union of every chain of semipime ideals of R is a semiprime ideal[8,Theorem 1.17].For an exchange ring we have the following result.Note that a subset I of a ring R is right T-nilpotent in case for every sequence a1,a2,...in I there is an n such that an...a1=0.

Theorem 1.1 Let R be an exchange ring with primitive factors Artinian.If the Jacobson radical of any indecomposable homomorphic image of R is right T-nilpotent and if any indecomposable homomorphic image of R is semiprime,then R is von Neumann regular.

Proof Assume that R is not regular.There exists a∈R such that a is not in aRa.Set

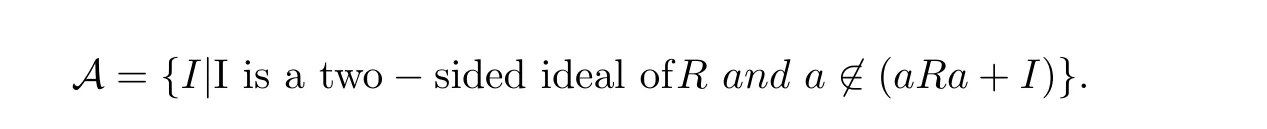
Since the zero ideal is in A,A is not empty.Given any chain{Iα,(α ∈ Λ)}in A,where Λ is an indexed set,set I= ∪α∈ΛIα,then I is a two-sided ideal of R.If I is not in A,a ∈ aRa+I.There must be an integer k such that a∈aRa+Ik,which is a contradiction.Thus the union of every chain in A is again in A.By Zorn’s Lemma,A contains a maximal element A.

We first claim that R/A is indecomposable as a ring.If not,then there exist ideals J,K of R such thatand R/A=J/A⊕K/A.And hence J∩K=A since J/A∩K/A=0.By definition of A,there exist x,y∈R such that a−axa∈J and a−aya∈K.Then we have a−a(x+y−xay)a=a−axa−(a−axa)ya=a−aya−ax(a−aya)∈J∩K.So a−a(x+y−xay)a∈A,which is a contradiction.Hence R/A is indecomposable as a ring.

Suppose that J(R/A)is right T-nilpotent.If A is a prime ideal of R,we claim that J(R/A)=0.Assume to the contrary that there exists a non-zero a in J(R/A).Then there exist x1,x2,...∈R/A such that ax1a 6=0,ax2ax1a 6=0,...,axn...ax1a 6=0,....Since J(R/A)is T-nilpotent,we obtain a contradiction.Thus J(R/A)=0.Since R is an exchange ring with primitive factor Artinian,so is R/A.By Nicholson[10,Proposition 1.4],every homomorphic image of an exchange ring is exchange.So R/A is an exchange ring.It is easy to see that exchange rings are I0-rings.Using[15,Lemma 3.7],we see that R/A is simple Artinian,hence it is regular,which contradicts the choice of A.Then we assume that A is not prime.Consequently,we have two-sided ideals K,L of R such thatand KL⊆A.Set K0={r∈R|rL⊆A},and set L0={r∈R|K0r⊆A}.Since A is a semiprime ideal by hypothesis,the ideals K0and L0are semiprime.Since(K0∩L0)2⊆K0L0⊆A,((K0∩L0)/A)2=0,i.e.,(K0∩L0)/A is a nilpotent ideal of R/A.Note that,since A is semiprime,K0∩L0⊆A.It is clear that K⊆K0and L⊆L0,hence the ideal K0and L0properly contain A.By the maximality of A,we have that a∈aRa+K0,a∈aRa+L0.Thus a∈aRa+K0∩L0⊆aRa+A,a contradiction.Thus R is regular.

Example 1.2[9,Example1.3]The condition that the Jacobson radical of any indecomposable homomorphic image of R is T-nilpotent is not superfluous.Let Q be the field of all rationals and S the ring of all rationals with odd denominators.Let R={(x1,...,xn,s,s,...)|n≥1,xi∈Q,s∈S}.S has a unique maximal ideal(2),where p is odd.Thus J(S)6=0,and S is not regular.By the proof of Theorem 1.1,S is not T-nilpotent,since S is a prime ring.Since S is a homomorphic image of R,the condition that the Jacobson radical of any indecomposable homomorphic image of R is T-nilpotent is not satisfied,and R is not regular.

Corollary 1.3 Let R be a weakly P-exchange ring with primitive factors Artinian.If any indecomposable homomorphic image of R is semiprime,then R is von Neumann regular.

Proof Let Q be an ideal of R.Since R is a weakly P-exchange ring,so is R/Q by[11,Proposition 4.1].And by[10,Proposition 2.11]J(R/Q)is T-nilpotent,then R is regular by Theorem 1.1.

Recall that a ring is called left(right)quasi-duo if every maximal left(right)ideal is twosided.It is easy to prove that a left(right)quasi-duo ring is with left(right)primitive factors Artinian.We have the following corollary.

Corollary 1.4 For a right or left quasi-duo exchange ring R,if J(R/Q)is T-nilpotent for any ideal Q of R and if any homomorphic image of R is semiprime,then R is von Neumann regular.

Proof Since quasi-duo rings are with primitive factors Artinian,by Theorem 1.1,the assertion is true.

Corollary 1.5 Let R be an exchange ring of bounded index.If the Jacobson radical of any indecomposable homomorphic image of R is T-nilpotent and if any indecomposable homomorphic image of R is semiprime,then R is von Neumann regular.

Proof By virtue of[16,Theorem 3],we know that R is an exchange ring with primitive factors Artinian,so we can check it applying Theorem 1.1.

Recall that a ring R is called an Abelian ring if all idempotents of R are central.We have the following corollary.

Corollary 1.6 Let R be an Abelian exchange ring with J(R)=0.If the Jacobson radical of any indecomposable homomorphic image of R is T-nilpotent and if any indecomposable homomorphic image of R is semiprime,then R is von Neumann regular.

Proof For an exchange ring R with zero Jacobson radical,idempoents are central i ffR contains no nonzero nilpotent element[11,Lemma 4.10].Thus R is abelian i ffR is of bounded index 1.By Corollary 1.5,R is regular.

Corollary 1.7 Let R be a ring satisfying one of the following conditions:(1)R/J(R)is an exchange PI-ring;(2)for any finite or countably infinite many of orthogonal idempotents e1,e2,...and any x1,x2,...in R,there exists an integer n>0,such that e1x1e2x2...enxn∈J(R);(3)R/J(R)is an exchange ring with finite orthogonal noncentral idempotent elements.If the Jacobson radical of any indecomposable homomorphic image of R is T-nilpotent and if any indecomposable homomorphic image of R is semiprime,then R is von Neumann regular.

Proof It follows from[14,Corollary 2.4],[14,Theorem 2.5],[14,Corollary 2.6]and Theorem 1.1.

Proposition 1.8 Let R be a semiprimitive exchange ring with a finite set of orthogonal idempotents.Then R is von Neumann regular.

Proof By[5,Corollary 2],R is semiperfect.Since R is semiprimitive,R is semisimple.So R is regular since semisimple rings are regular.

Corollary 1.9 Let R be an exchange ring with a finite set of orthogonal idempotents.Then R/J(R)is von Neumann regular.

Proof R/J(R)is an exchange ring with a finite set of orthogonal idempotents,since idempotents can be lifted modulo J(R).Since R/J(R)is semiprimitive,by Proposition 1.8,it is regular.

It is well-known that von Neumann regular rings are π-regular,but there is a π-regular ring that is not regular[12,Proposition 23.4(2)].We have the following results,since π-regular rings are exchange rings.

Corollary 1.10 (1)Let R be a semiprimitive π-regular ring with a finite set of orthogonal idempotents.Then R is von Neumann regular.

(2)Let R be a semiprime π-regular ring with a finite set of orthogonal idempotents.Then R is von Neumann regular.

Corollary 1.11 (1)Let M be a module with the finite exchange property.If J(End(M))=0,and End(M)has a finite set of orthogonal idempotents,then End(M)is von Neumann regular.

(2)Let M be an indecomposable module with the finite exchange property.If J(End(M))=0,then End(M)is von Neumann regular.

Proof (1)It is clear.

(2)Since M is indecomposable,End(M)has only two orthogonal idempotents.By(1),End(M)is von Neumann regular.

§2.Exchange Rings with Prime Factors Artinian

It is well-known that for a regular ring the following conditions are equivalent:each of its left(right)primitive factors is Artinian and each of its prime factors is Artinian[8,Theorem 6.2].But for exchange ring it is not true.In fact,recall that Yu[15,Theorem 2.1]proved that the exchange ring with prime factors Artinian is strongly π-regular,but he also gave an example of an exchange ring with primitive factors Artinian which is not strongly π-regular[15,Example 3.5]yu1.Kaplansky once made the following conjecture:A ring R is von Neumann regular if and only if R is semiprime and each prime factor ring of R is von Neumann regular.However,the conjecture failed in general[8,Example 1.19]go.Luckily,the conjecture holds for commutative rings[7].We have the following properties.

Proposition 2.1 Let R be a commutative exchange ring with prime factors Artinian.If R is semiprime and J(R/P)=0 for any prime ideal P,then R is von Neumann regular.

Proof By the Kaplansky’s conjecture for the commutative ring R,it is regular i ffit is semiprime and R/P is regular for any prime ideal P.It suffices to check that R/P is regular for any prime ideal P.Since R is an exchange ring with prime factors Artinian,So is R/P.Since every left primitive ring is a prime ring,R/P is a ring with primitive factors Artinian.It is easy to check that exchange rings are I0-rings.Since every prime ring is indecomposable as a ring,so is R/P.By[15,Corollary 3.7],R/P is simple Artinian,whence is regular.

Proposition 2.2 Let R be an exchange ring with prime factors Artinian.If all ideals of R are idempotent and J(R/P)=0 for any prime P,then R is von Neumann regular.

Proof Recall that a ring is regular i ffall of its ideals are idempotent and all of its prime factors are regular[8,Corollary 1.18].It is sufficient to check that any prime factor R/P is regular,which follows from the proof of Proposition 2.1.

§3.Exchange Rings of Bounded Index

It is well-known that a regular ring R has index at most n,then all primitive factor rings of R are Artinian with length at most n[8,Corollary 7.10].This is also true for exchange rings[16,Theorem 3].We have the following results.

Theorem 3.1 Let R be an exchange ring of bounded index n.For any prime ideal P of R,if J(R/P)=0,then R/P is von Neumann regular.

Proof We first show that R/P contains at most n orthogonal idempotents for any prime ideal P of R.

It is easy to check that rn=e1x1e2x2e3...enxnen+1,and rn+1=0.Since R has bounded index n,rn=0.It is a contradiction,since rn/∈P.

Exchange rings containing a finite set of orthogonal idempotents are semiperfect[5,Corollary 2].since J(R/P)=0,R/P is semisimple.Since semisimple rings are regular,so is R/P.

Corollary 3.2 Let R be an exchange ring of bounded index n.Then primitive factors are regular.

Proof Since primitive rings are semiprimitive and prime,it is true following from Theorem 3.1.

Recall that an ideal P of R is called a minimal prime ideal of R if P is a minimal element of the set of all prime ideals of R.By Zorn’s Lemma,Every prime ideal of R contains a minimal prime ideal of R.

We call a ring R has nil-property if the Jacobson radical of homomorphic image of R is a nil ideal.It is clear that the π-regular ring has nil-property.

Lemma 3.3 Let R be a semiprime ring of index at most n.If R has nil-property,then R is semiprimitive.

Proof Let N be the prime radical of R.Let h:R→R/N be the natural epimorphism.By[12,Remark 14.4],h(R)is a semiprime ring of index at most n.By[12,Corollary 14.3],h(R)does not have nonzero nilideals.Since J(R)is a nilideal,h(J(R))is a nilideal of h(R).Then h(J(R))=0.Therefore J(R)⊆N⊆J(R).By[12,Remark 3.7],J(R)=0.

Lemma 3.4 Let R be an exchange ring of index at most n.If R has nil-property and if Q is a prime ideal of R,then R/Q is a simple Artinian ring of index at most n.

ProofQ contains a minimal prime ideal of R,named P.Set¯R≡R/P.By[12,Remark 14.4],¯R is a prime ring of index at most n.By[12,Remark 14.5],¯R is an ring without infinite orthogonal idempotents.since every homomorphic image of an exchange ring is exchange,by[5,Corollary 2],¯R is semiperfect.By Lemma 3.3,¯R is semisimple.Since¯R is prime,¯R is simple.Thus R/Q is a quotient of R/P and is a simple Artinian ring.

Proposition 3.5 Let R be an exchange ring such that every left primitive factor ring of R is a ring of index at most n.If R has nil-property,then every indecomposable semiprimitive factor ring of R is von Neumann regular.

ProofLet¯R be an indecomposable semiprimitive factor ring of R.Since every homomorphic image of an exchange ring is exchange and every exchange ring is I0-ring,by[12,Proposition 15.8],¯R is a simple ring.since simple rings are primitive,and primitive rings are prime,¯R is a prime exchange ring of index at most n.Thus by Lemma 3.4,¯R is a simple Artinian ring of index at most n.Thus¯R is regular.

Acknowledgments

The author wishes to express his gratitude to Professor Xiaosheng Zhu for his helpful suggestions and to the editor and the referees for their careful reading and comments,which improved the presentation of this article.