基于粒子群优化的马氏距离模糊聚类算法

祖志文，李 秦

(兰州交通大学 数理学院，兰州 730070)

0 引 言

模糊聚类是通过建立数据样本对类别的不确定性进行描述，表达样本类属的模糊性，该方法能够更客观地反应现实世界，具有较强的聚类效果与数据表达能力。模糊c均值聚类算法(fuzzy c-means algorithm，FCM)是经典的模糊聚类算法，马氏距离的模糊聚类算法(fuzzy c-means algorithm based on Mahalanobis distance，M-FCM)是将FCM中的欧氏距离用马氏距离替代，二者均是爬山迭代算法，对初始划分都比较敏感，容易陷入局部极值点，将粒子群算法(particle swarm optimization，PSO)与模糊聚类算法结合可有效实现对模糊聚类算法的优化。如文献[1]将PSO算法和FCM相结合，提出了一种新的模糊聚类算法PSO-FCM。文献[2]利用模糊系统对PSO算法进行改进后与FCM结合，实现全局最优。文献[3]设计结合类内紧致性和类间分离度的适应度函数改进PSO算法，提出改进的模糊聚类算法(Importance for fuzzy clustering algorithm based on particle swarm optimization，IFPSOFCM)。文献[4]提出了2种将PSO算法与FCM算法混合的优化算法来解决FCM算法的缺陷。文献[5]提出了基于粒子群优化的自适应神经模糊推理系统的信道均衡器。文献[6]设计了一种利用局部空间信息和偏差校正的目标函数进行模糊熵聚类，再通过改进的粒子群算法进行优化，使得算法具有新的适应性能。

本文将基于粒子群算法对马氏距离模糊聚类进行优化，构造新的粒子适应度函数，提出一种基于粒子群优化的马氏距离模糊聚类算法(Mahalanobis distance fuzzy clustering algorithm based on particle swarm optimization，DPSOM-FCM)。

1 基于马氏距离的模糊聚类算法M-FCM

将FCM算法中的欧氏距离用马氏距离代替，可以消除量纲不同对聚类分析的影响，排除变量之间相关性的干扰，便于处理复杂的多维数据[7]。

FCM算法的优化目标函数为

(1)

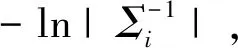
i=1,2,…,c;j=1,2,…,n)

(2)

最小化J，对ci,uij,Σi求偏导，令其结果为零可得

(i=1,2,…,c;j=1,2,…,n)

(3)

(4)

(5)

M-FCM算法描述如下。

初始化：给定聚类类别数c，2≤c≤n，n是数据个数，设定迭代阈值ε=1×10-5，取一般值m=2，初始化聚类中心矩阵C(0)，设置迭代计数器L=0。

步骤1用(3)式计算或更新隶属度矩阵U(L)。

步骤2用(4)式更新聚类中心矩阵C(L+1)。

步骤3如果‖C(L)-C(L+1)‖<ε，则算法停止并输出隶属度矩阵U和聚类中心C，否则令L=L+1，转向步骤1。其中，‖•‖为合适的矩阵范数。

2 粒子群算法(PSO)

粒子群算法PSO由Eberhart和Kennedy受鸟群觅食行为的启发于1995年提出[8]。通常，粒子群算法的数学描述为：设在一个D维空间中，由N个粒子组成的种群X={S1,…,Si,…,SN}，其中，第i个粒子Si的位置为xi=(xi1,xi2,…,xiD)′，其速度为vi=(vi1,vi2,…,viD)′。它的个体极值为pb=(pi1,pi2,…,piD)′，种群的全局极值为pg=(pg1,pg2,…,pgD)′，为追随当前最优粒子，粒子xi将按照(6)式、(7)式改变自己的速度和位置。粒子在解空间内不断跟踪个体极值与全局极值进行搜索，直到达到规定的迭代次数或满足规定的误差为止。

vij(t+1)=wvij(t)+c1r1(t)(pij(t)-xij(t))+c2r2(t)(pgi(t)-xij(t))

(6)

xij(t+1)=xij(t)+vij(t+1)

(7)

(6)—(7)式中：j=1,2,…,D；i=1,2,…,N；N为种群规模；t为当前进化代数；w为1998年Eberhart和Shi引入到PSO算法速度项中的系数[9]，即惯性权重；r1,r2为分布于[0,1]的随机数；c1,c2为加速系数[10]。

在粒子群算法中，粒子的优劣好坏需要适应度函数来进行评价，根据适应度函数值即适应值寻找粒子的状态极值，对粒子进行选择，优胜劣汰，从而更新其他粒子的状态。粒子的适应值越大，即该粒子的质量越好，越适应目标函数所定义的生存环境。

3 利用粒子群优化马氏距离模糊聚类算法

3.1 算法思想

如前所述，M-FCM算法由于使用梯度迭代法寻找最优解，存在对初始值敏感和容易陷入局部最优解的缺陷，为此将粒子群算法加入到M-FCM算法中。本文提出的基于粒子群优化的马氏距离模糊聚类算法的设计思想如下。

1)为寻找最优聚类结果，即确定合理的聚类中心，选取聚类中心作为种群中的粒子，一个粒子表示一种聚类划分的情况，粒子的每一维表示聚类一个簇的质心，最优聚类中心即最优粒子。

2)对于粒子的评价，为使好的模糊聚类划分使类内样本尽可能地紧凑、类与类之间尽可能地分离，并且模糊聚类划分尽可能地清晰，本文从类内紧致度、类间分离度与类间清晰度的角度综合考虑，设计适应度函数为

fitness(xi)=α·compact(U,C,Σi)+

(8)

(8)式中：α(0<α<1)为适应度函数系数；(8)式等号右边第1项为衡量目标的类内紧致度函数，第2项为衡量目标的类间分离度函数，第3项为衡量目标的类间清晰度函数。用目标函数的均值来衡量类内紧致度，目标函数越小紧致度越佳。

(i=1,2,…,c;j=1,2,…,n)

(9)

用类间聚类中心的总距离来定义类间分离度，分离度大的数据倾向于不同的类别属性，记Dik为群体最优位置粒子的内部距离，即最优聚类中心距，当separate(Si)越大时，类间分离程度越好。

(i,k=1,2,…,c)

(10)

把各个类内最大模糊隶属度值的均值作为衡量类间的清晰度

(i=1,2,…,c;j=1,2,…,n)，

(11)

当definite(U)越小时，模糊聚类划分结果越清晰。综上，fitness(xi)的值越小，说明样本集的类内紧致程度越高、类间分离程度越大、类间清晰程度越明显，即fitness(xi)的值越小，粒子越好。

另外，算法终止条件为以下2种情况：①最优解对应的目标值保持不变或变动小于阈值ε；②迭代次数已达到设定的最大次数itermax。满足任一种情况算法终止。

3.2 算法步骤

把基于粒子群优化的马氏距离模糊聚类算法记为DPSOM-FCM，算法具体步骤如下。

输入：数据集、类别数。

1)算法参数设置，包括算法最大迭代次数itermax、最小阀值ε，模糊加权参数m，粒子种群大小N，粒子速度更新公式中的加速系数c1,c2及线性递减的惯性权重参数wmax,wmin，适应度函数系数α。

2)对粒子编码，设置粒子的初始位置x0和初始速度v0，初始化模糊聚类的隶属矩阵U0和聚类中心C0。

3)设置每个粒子的pb0,pg0，计算粒子的适应值fitness0，并储存。

4)进行迭代，由M-FCM算法更新隶属度矩阵U和聚类中心C。

5)计算惯性权重w。

6)更新每个粒子的速度和位置vi,xi。

7)计算每个粒子的pb,pg。

8)更新粒子的适应值fitness，并储存。

9)对于每个粒子，将其适应度值与所经历过的最优位置pb的适应值进行比较，若较好，则将其作为当前的个体最优位置。

10)对于每个粒子，将其适应值与全局经历过的最优位置pg的适应值进行比较，若较好，则将其作为当前全局最优位置。

11)如果全局最优位置适应值相对上次的改变量小于特定的最小阀值ε或达到最大迭代次数，则结束，否则转向步骤4)。

输出：最优聚类中心及适应值。

4 实验结果与分析

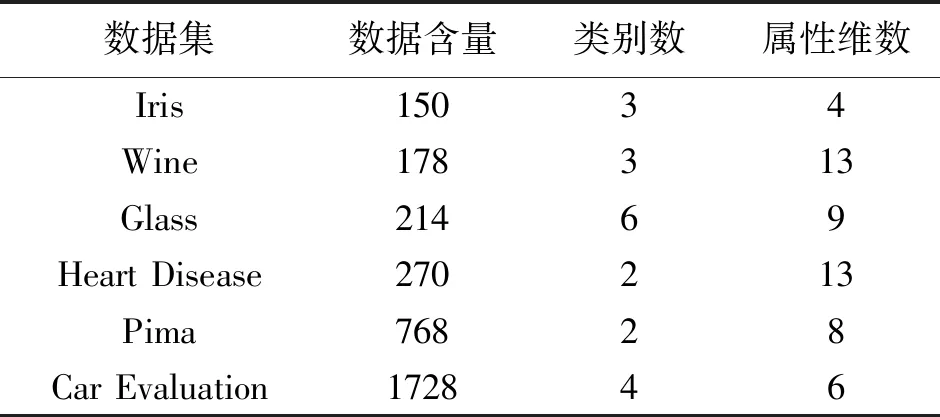
为验证本文提出的基于粒子群优化的马氏距离模糊聚类算法DPSOM-FCM的收敛性和聚类能力，采用来自UCI数据库中的6个数据集进行仿真实验。实验数据集的构成介绍如表1所示。在各数据集上DPSOM-FCM算法的适应值变化如图1所示。将DPSOM-FCM算法与FCM，M-FCM算法及文献[1]中PSO-FCM与文献[3]中IFPSOFCM算法进行聚类有效性和聚类准确性对比分析，实验结果如表2、表3所示。其中，选取的有效性指标[3]为常用有效性指标PC(partition coefficient)，MPC(my partition coefficient)，PE(partition entropy)，FS(Fukuyama and Sugeno)。

图1 各数据集上DPSOM-FCM算法的适应值变化Fig.1 Fitness function value changes of DPSOM-FCMalgorithm on each data set

数据集数据含量类别数属性维数Iris15034Wine178313Glass21469Heart Disease270213Pima76828Car Evaluation172846

实验环境为电脑系统Inter Pentium处理器，型号为 B960，频率为2.20 GHz，4.00 GB内存，运行均用Matlab语言实现。实验参数设置为：N=20,c1=c2=m=2,wmax=0.9,wmin=0.4,α=0.6，算法最大迭代次数为100次，最小阀值为1×10-5，进行重复聚类实验20次，实验结果取均值。

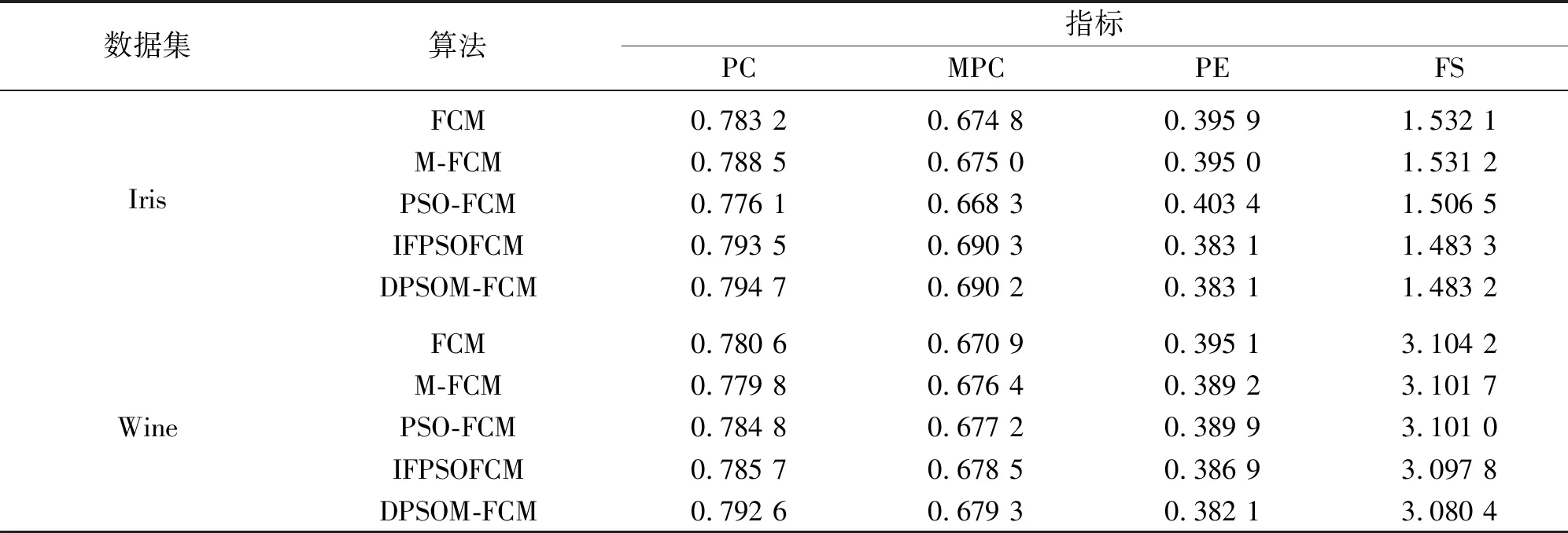
表2 5个算法的聚类有效性对比

续表2

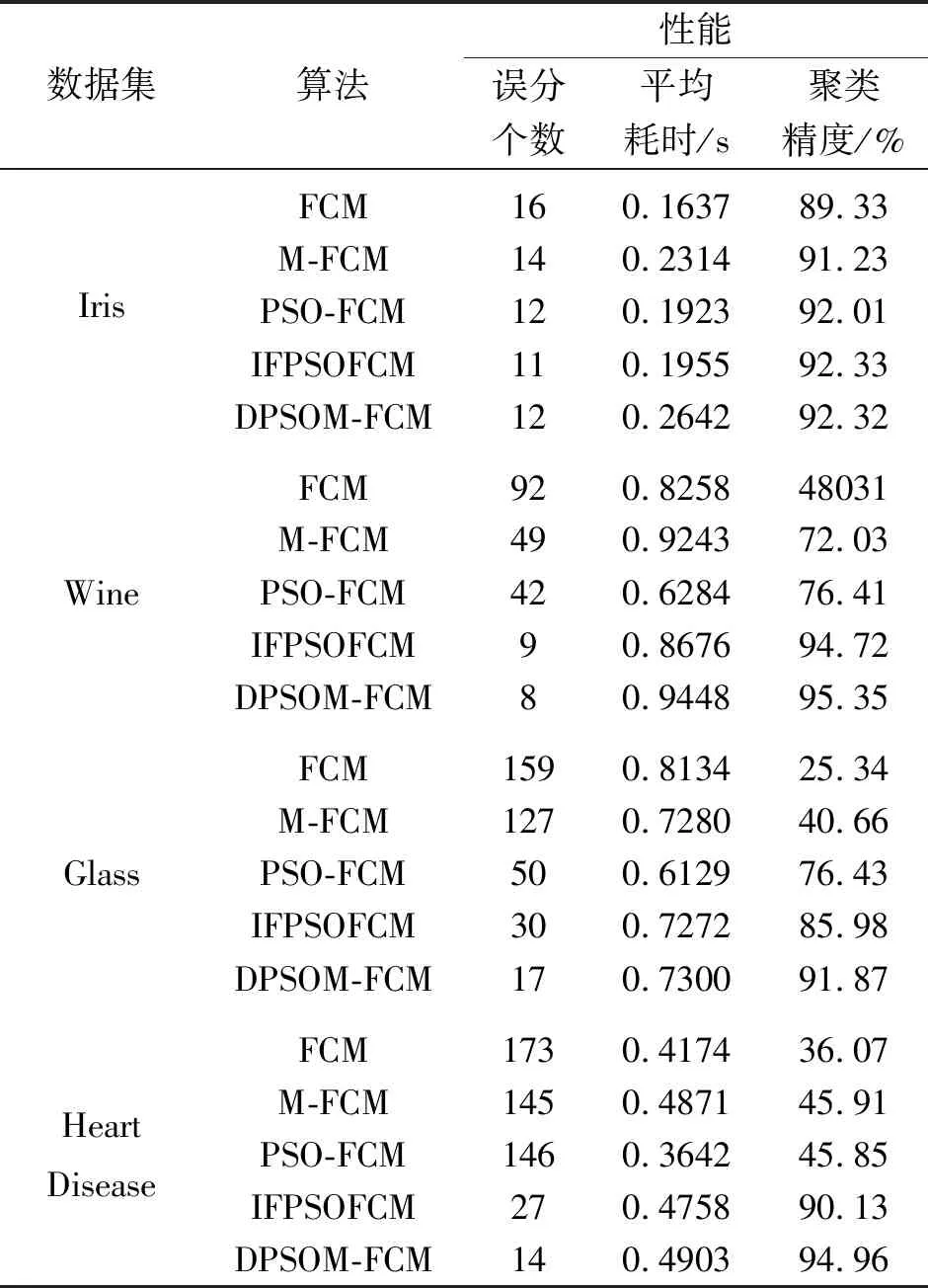
表3 5个算法的聚类准确性对比

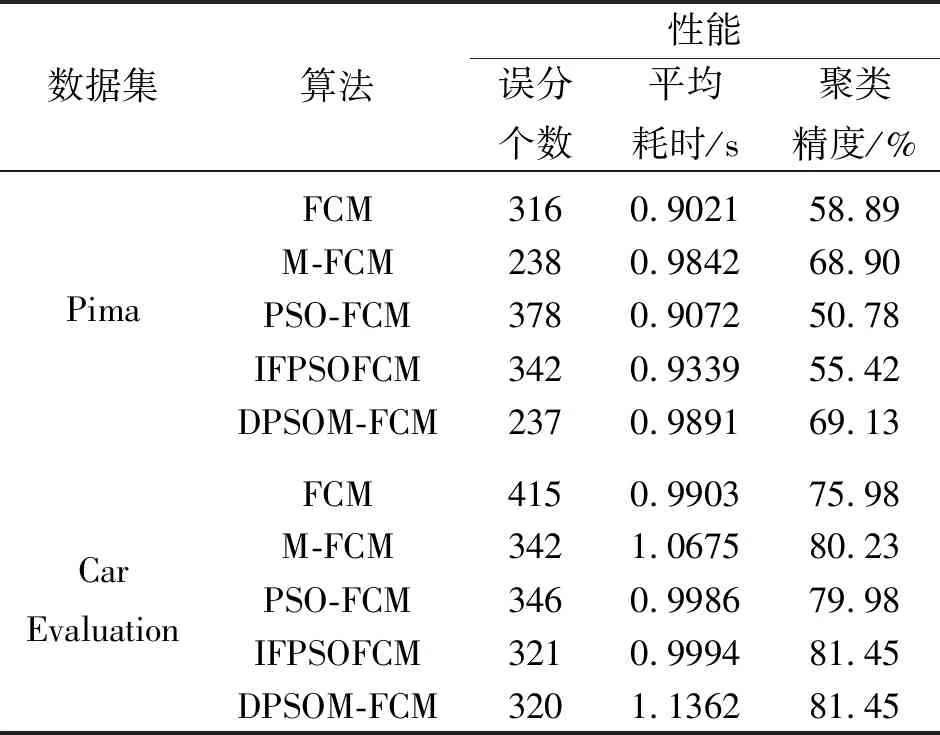
续表3

实验分析：由图1可知，DPSOM-FCM算法在6个数据集上收敛且速度较快。由于有效性指标PC与MPC越大、PE与FS越小,聚类越有效，故由表2得出DPSOM-FCM算法具有优于其他算法的类间分离性和类内紧凑性，可以证明在基于粒子群优化的模糊聚类中，本文构造的适应度函数有助于算法寻找最优聚类粒子。另一方面，由表3可知：①经过粒子群优化的PSO-FCM，IFPSOFCM和DPSOM-FCM算法聚类精度普遍高于未经过优化的FCM，M-FCM算法，即结合粒子群算法的模糊聚类具有全局寻优性，聚类更加准确，起到了对模糊聚类的优化作用；②在Iris与Car Evaluation数据集上，FCM耗时最短，DPSOM-FCM耗时最长但精度高；在3组高维数据集Wine，Glass，Heart Disease上，PSO-FCM耗时最短但聚类精度不稳定，DPSOM-FCM的聚类误分个数明显减少，且聚类精度高于PSO-FCM和IFPSOFCM算法；在类间相互交叠的数据集Pima上，M-FCM与DPSOM-FCM算法聚类精度都高于其他算法。这说明对于高维复杂数据集，基于粒子群算法以马氏距离为度量的模糊聚类效果优于以欧氏距离为度量的模糊聚类；③马氏距离的计算复杂。由于本文提出的算法DPSOM-FCM比传统模糊聚类算法加入了粒子群优化步骤，所以DPSOM-FCM算法的运行速度不具优势，但仍在合理耗时内。

5 结束语

通过对粒子群算法和马氏距离模糊聚类算法的研究，构造将类内紧致度、类间分离度与类间清晰度结合的适应度函数，本文提出了基于粒子群优化的马氏距离模糊聚类算法DPSOM-FCM。该算法用马氏距离替换FCM算法的欧氏距离，同时结合了粒子群的全局优化性能，经过在6个数据集上，与FCM，M-FCM，PSO-FCM， IFPSOFCM算法的实验对比分析，验证了该算法的收敛性、有效性和聚类准确性，具有全局优化作用。