改进的mRmR特征选择方法在人体行为识别中的应用
王华华,黄 龙,周远文,赵永宽
(重庆邮电大学 移动通信技术重庆市重点实验室,重庆 400065)
0 引 言
近年来,基于可穿戴传感器的人体行为识别的研究吸引了越来越多国内外学者的目光,通过将不同类型的传感器穿戴于身体的不同位置可实现对一些日常人体行为的识别与监测,另外在智能家居方面也具有广泛的应用前景[1-5]。基于惯性传感器的人体行为识别的整个流程中,随着提取特征维数的不断增加,必然会造成一些不相关及冗余特征的产生,那么特征选择将是非常重要的一个环节,提出一种行之有效的特征选择方法至关重要。特征选择数是从原始特征子集中选择一个重要的子集以改进学习系统,降低实验计算复杂度,并能提高识别准确率[6-9]。
在基于惯性传感器人体行为识别中,为了提高人体行为识别的准确率,研究者们往往会提取大量的时域频域特征,然而提取的特征维数不能无限增加,随着特征维数的增多,可能导致维数灾难的后果,所以一般在提取特征后,需要对提取的特征集进行降维,以达到去除不相关的冗余特征,降低计算复杂度并最终实现更好的分类效果。特征选择方法一般可以分为2类:基于包装器的方法与基于滤波器的方法[10]。文献[11]提出了基于滤波器的特征选择方法(Relief-F)[12]与基于封装器的特征选择方法相结合的使用方法。文献[13]提出一种基于博弈论的特征选择方法。文献[14]提出一种不一致进化特征选择方法,该方法通过设计不一致度量方法并通过遗传算法进行优化筛选特征子集。文献[15]提出一种基于遗传算法优化的加速度特征选择方法,达到一定的识别效果。但这些方法都存在着识别准确率不高,特征选择效果不好的问题。由于一些传统的过滤式特征选择方法只使用某一种相关性度量方法选择和衡量与分类类别相关性大的特征,如距离度量、一致性度量、信息度量和依赖性度量等方式,并赋予与类别相关性大的特征较高的权重。这些方法一方面仅考虑了特征与类别之间的相关性而忽略了特征之间的相关性,从而无法去除特征之间的冗余性;另一方面该类方法忽略了特征之间的交互作用可能对分类带来更好的效果,如一些特征在单独用于分类时并不能达到很好的效果,但当几种特征相互结合使用时可能起到较好的分类作用。虽然每种相关度量方式各不相同,但各种相关度量方法在不同的特征选择方法发挥着各自的作用,那么如何结合多种相关度量方式对特征子集进行特征选择将是本文研究的重点。
基于此,本文提出一种基于多种相关度量的特征选择方法,该方法首先通过融合多种性能优异的相关度量方法对筛选特征子集进行初步粗略降维,然后通过设计适应度函数,利用遗传算法搜索最优或者次优特征子集,从而进一步实现精细降维,并最终能有效降低特征维数,同时能实现较低的分类误差和较好的识别准确率。
1 基本知识描述
1.1 基于最小冗余与最大相关算法框架
由于特征选择方法的最终目的是通过有效的方法去除不相关特征和冗余特征,从而选择出对分类有效的相关特征子集。因此,本文提出的特征选择方法将基于经典的最小冗余与最大相关准则(mRmR)特征选择方法的理论框架,可以用(1)式表示为
J(F)=D(F)-R(F)
(1)
(1)式中:D(F)表示特征与类别之间的相关性;R(F)表示特征与类别之间的冗余性。
1.2 相关性度量方法
1)最大信息系数(maximal information coefficient,MIC)是一种有效的统计量度量方法,主要用于评估2个变量之间的关联。MIC克服了互信息直接用于特征选择时没办法归一化,在不同数据集上的值无法做比较,且对连续变量计算麻烦的缺点。当拥有足够的统计样本时,MIC可以捕获广泛的关系,而不限定于特定的函数类型(如线性、指数型、周期型等)。一般的相关系数只能度量线性关系,然而在一些现实应用中非线性是广泛存在的,包括周期性、指数关系等。MIC不依赖测量数据的统计分布,与以前的研究相比,可以识别广泛类型的关联。为了解决这个问题,研究者们提出了一种新颖的相关度量方法“最大信息系数”,可以用(2)式表示为
(2)
(2)式中,I(X;Y)表示变量X与变量Y间的互信息量。
2)皮尔逊相关系数(pearson correlation coefficient,PCC)是基于数据矩阵的协方差矩阵,是评估2个向量之间关系强度的一种方法。它的值为[-1,1],其中,1表示变量完全正相关,0表示无关;-1表示完全负相关。通常,2个变量X和变量Y之间的皮尔逊相关系数可以用(3)式表示为
(3)
1.3 遗传算法
遗传算法是一种模拟自然界生物遗传和进化过程而形成的高效全局优化搜索算法。该算法通过群体搜索来寻找群体最优解。它具有鲁棒性强、简单通用等优点,并在很多领域应用广泛。遗传算法的主要步骤包括确定实际问题的参数集、遗传编码、初始化群体、设计适应度函数及遗传操作(包括选择、交叉、变异)。其中,最重要的操作之一就是设计适应度函数,通过以适应度函数作为评价标准,主要用于评价个体的优劣程度,因此,适应值高的个体被选中的概率高,群体中的个体通过不断的选择、交叉、变异等迭代操作,最终可以获取问题的最优解。遗传算法主要有以下几个步骤。
①初始化群体。对于人体行为识别中的特征选择问题,采用二进制对问题的解进行编码是比较好的方法,本文对已实现部分降维的特征子集进行二进制编码,通过二进制数字1与0来表示对应特征的有无。如果原始特征维数为G维,则问题的一个解可以通过一个G维0-1向量来表示。当第i个特征为1时表示第i个特征被挑选为特征子集之一;反之,如果向量的第i个分量为0则表明没有选择第i个特征。如此,一个特征子集就可以通过一个G维0-1向量表示。
②适应度函数设计。为了实现更好的分类识别准确率,遗传算法需要设计合适的适应度函数。那么特征选择的最终目的还是通过降低特征维数,降低计算复杂度,进而获取更高的分类识别准确率,所以本文将分类识别准确率作为适应度函数,换句话说就是让能使分类准确率高的特征被选择。
③选择。通过选择策略从群体中选出优良个体,淘汰劣质个体。本文采用适应值比例选择方法,那么个体的选择概率可以用(4)式表示为
(4)
(4)式中:a表示群体规模;fk表示个体的适应值。
④交叉。交叉是一个进化过程,是指把2个父代个体的部分结构加以替换重组而生成新的个体的操作。
⑤变异。变异是维持种群多样性的遗传算子,通过较小的概率对特征子集编码串上的某些位的值进行随机翻转,如0变1或1变为0等操作,从而产生新的个体。
2 本文方法描述
本文提出的特征选择方法主要分成2部分:第1部分提出基于mRmR准则的多种相关度量系数融合的特征选择方法,通过结合2种相关系数的优点,挑选部分相关性强且较少冗余的特征子集,以实现部分降维;第2部分,由于第1部分特征选择方法主要考虑特征与类别的相关性和冗余性,没有很好地考虑特征之间的交互作用,即一些特征在单独用于分类时效果不佳,但当几种特征结合使用时却可以实现较好的分类。因此,本文进一步提出通过遗传算法对第1部分提出的特征选择方法提取的特征子集进行优化。
2.1 多种相关系数融合
相关是度量2个变量关系的重要指标。它在信号处理中具有很多理论基础,例如匹配滤波,循环自相关检测等。在统计学中,可以通过不同的相关系数来描述各种变量之间的关系。这些相关系数很多被应用于特征选择方法中,相关性度量方法有很多种,常见的包括距离相关系数、最大信息系数、组内相关系数、决定系数、秩相关和皮尔逊相关系数等。基于此,为了更好地利用并结合2种不同相关度量方法的优势,本文通过融合2种相关性度量系数,即MIC和PCC,并定义该相关性度量系数MPC(X,Y)为
(5)
于是,若YL={y1,y2,…,yl}表示类别变量,l表示类别总数,F={F1,F2,…,Fi,…,Fm}表示特征集合,m表示特征总数,根据有监督的特征选择,特征Fi与类别标签YL的相关度量系数定义为
(6)
(6)式中:F表示特征集合;YL表示类别变量;Fi表示第i个特征。
根据最大相关与最小冗余准则中的最大相关原则,被选择的特征Fi应该与类别YL具有最大相关性,即为D(Fi,YL)取最大值时的Fi,记为Fmax,表示为
Fmax=argmaxD(Fi,YL)
(7)
同理,根据mRmR中的最小冗余准则,被挑选的特征Fi具有最小冗余性,计算冗余度大小可以表示为
Fmin=argminR(F)
(8)
传统的mRmR方法主要通过计算特征与类别之间的相关性及特征之间的冗余性进行筛选,去除不相关及冗余特征,以获取相关特征,而该方法没有很好的考虑特征间的交互作用对分类产生的积极作用。然而,在实际应用中通常使用增量搜索方法来获取由Φ(·)定义的近似最佳特征,算子Φ(D,R,M)用来定义优化最大相关和最小冗余信息。通过结合D与R,那么最优选择特征Fopt挑选准则表示为
Φ=D-R+M
Fopt=argmaxΦ(D,R,M)
(9)
由此,如果实验已经获取了k-1个特征的特征子集Fk-1,那么第k个特征Fk需要从特征集合{F-Fk-1}中挑选,则通过Φ(D,R,M),Fk的详细挑选准则表示为
(10)
2.2 初选特征获取方法描述
基于最大相关与最小冗余准则(mRmR)框架下,获取的特征子集是通过逐步更新挑选的。基于2种不同相关系数的融合,并通过(10)式获取最大相关与最小冗余特征子集。该方法首先初始化将需要构建的特征子集置为空集并设置预期获取特征维数s,然后将(10)式作为程序获取下一个特征的准则。本文提出的详细特征选择方法的伪代码如算法1所示。
算法1基于最小冗余与最大相关准则下的多种相关度量系数融合的特征选择方法。
输入:数据集X∈Rn×m,类别标签为YL,特征全集为F,特征个数为s
初始化:构建目标特征子集Fs=∅,则剩余特征子集Fa=F-Fs
fork=1 tosdo
对于剩余特征集Fa中的任意特征Fj,特征全集为F中的任意特征Fi,当挑选新的特征Fk的准则为
更新Fs=Fs∪Fk和Fa=Fa-Fk
end for
输出:Fs
2.3 基于遗传算法优化
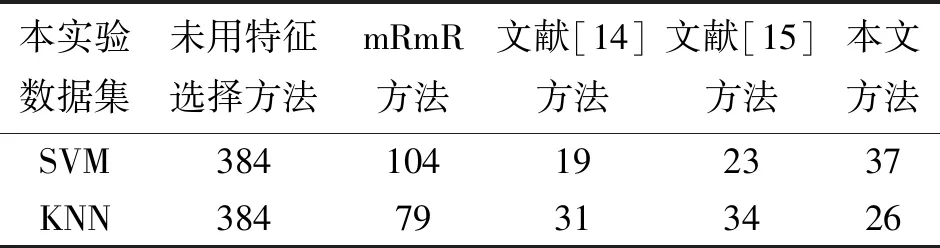
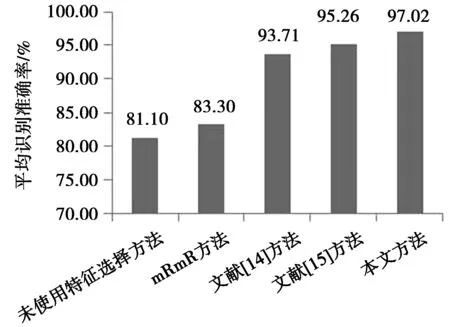
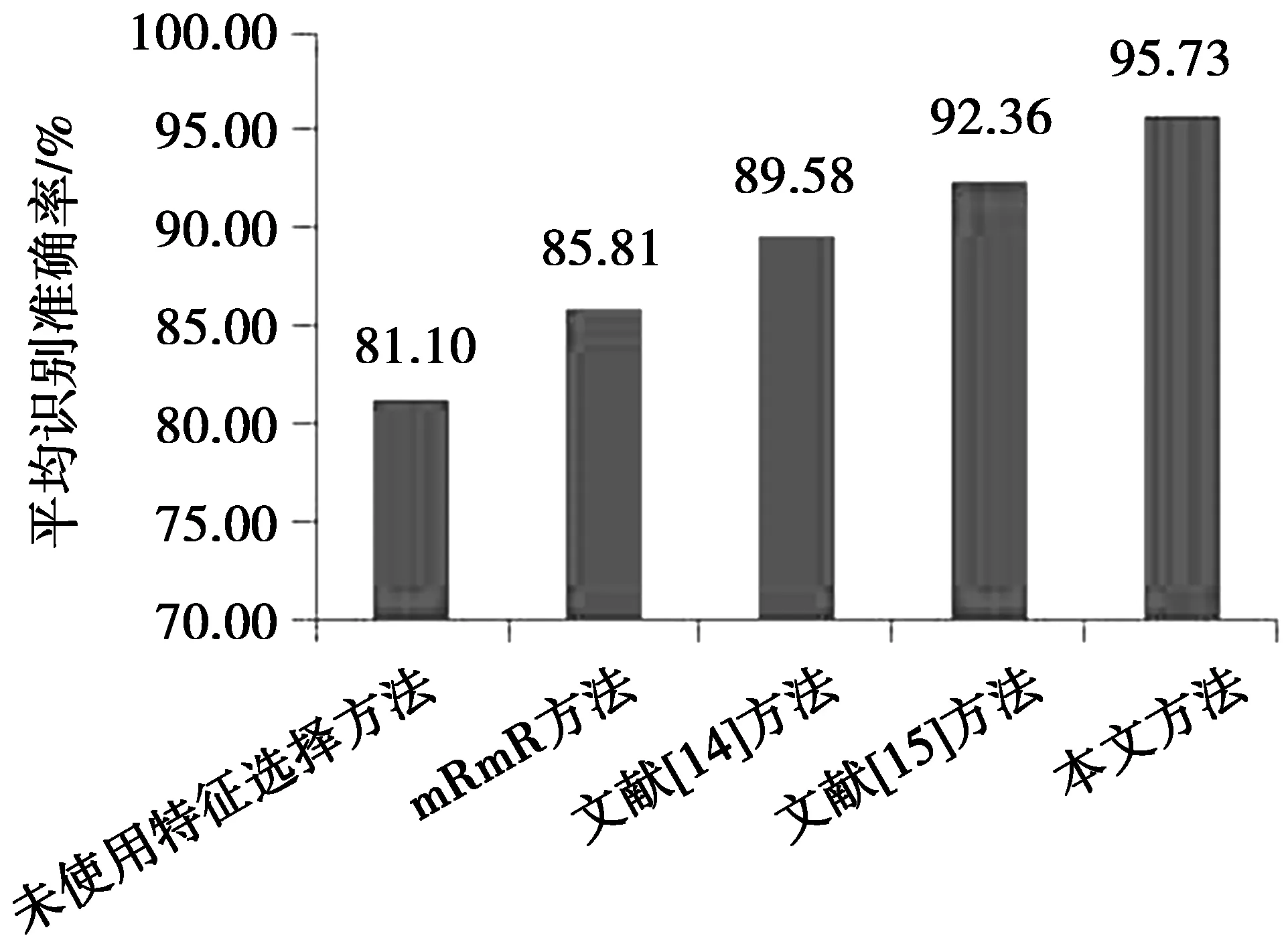
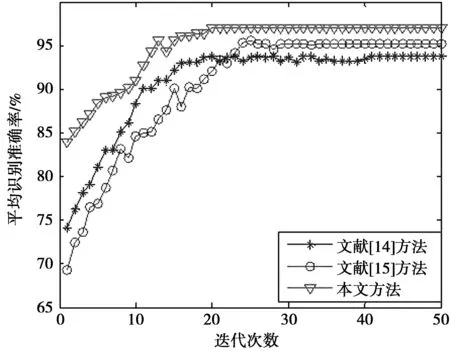
对2.2节获取的初选特征进行二进制编码,并通过遗传算法搜索最优或者次优特征子集。本文提出的基于遗传算法优化的多种相关度量特征选择的整体框图如图1所示。从图1可以看出,首先通过提出的基于mRmR准则下2种相关系数融合的特征选择方法对m维的原始特征子集进行降维,得到s(s 图1 基于遗传算法优化的特征选择方法Fig.1 Feature selection method based on genetic algorithm optimization 本文使用的数据集是来自实验室设计的可穿戴惯性传感器平台。该平台主要由2个模块组成:数据采集模块和数据接收模块。数据采集模块是由采集频率为50 Hz的惯性传感器、无线数据发送模块、电源模块、天线模块及腰带组成,如图2。数据接收模块由无线蓝牙模块、USB转串口模块及天线模块组成,如图3。有研究表明,人体行为频率低于18 Hz,因此,采集频率为50 Hz的传感器模块能满足实验要求。本实验邀请了18名实验者参与了人体日常行为数据的采集工作,通过将传感器数据采集平台置于实验者腰部,分别提取了坐立、站立、躺卧、步行、上楼、下楼、跑步等7种人体行为数据。每位实验者的每种行为数据采集时间至少2 min,并建立基本人体行为数据库。 图2 传感器信号采集模块Fig.2 Sensor signal acquisition module 首先,在数据预处理阶段,实验需要对原始数据信号进行低通滤波,去除原始信号中由于传感器抖动、外界干扰信号产生的噪声等成分,避免对最终的行为分类造成干扰;常见的去噪方式主要包括低通滤波、平滑滤波和取导数操作等方式,通过对3种不同方法去噪效果比较,本文采用的是FIR低通滤波器。有研究表明,人体动作的信号频率不超过18 Hz,因此,本文采用的低通滤波器截止频率设置为18 Hz,以去除原始信号中的高频噪声成分。在数据分割阶段,本实验采用的滑动窗口长度设置为2.5 s,考虑到传感器的采集频率为50 Hz,因此,每个数据窗口有125个数据点,窗口重叠率设置为50%,本数据集一共包含6 048个特征样本,每种行为包含864个特征样本。为了建立与用户无关的人体行为识别通用模型,实验采用留一交叉法(LOO)进行测试。根据不同分类行为将数据集划分为训练集和测试集,分别用于训练和测试分类模型。将每种不同行为的特征向量平均分成6个特征子集,然后每次不重复地抽取其中的一个特征子集作为待测样本集,剩余5个特征子集用于训练样本集,这样每次训练样本和测试样本分别包含720和144个特征样本,循环进行6次并对识别准确率求均值得出最终识别结果。表1为每次用于训练与测试时的样本数的划分情况。 图3 传感器数据接收模块Fig.3 Sensor signal receiving module 分类行为样本总数训练集样本数测试集样本数坐立54051030躺卧54051030站立54051030步行54051030上楼54051030下楼54051030跑步54051030 为了验证本文方法的性能,实验对滤波后的样本信号提取了包括均值、方差、四分位值、相关系数等348种特征,包括164种时域特征和184种频域特征,这样每种加速度行为的特征维数为384维。由于这些高维数据中存在着大量的相关与冗余信息,所以实验主要分成2部分完成:①通过本文提出的基于最大相关与最小冗余(mRmR)框架下的2种相关度量系数融合的特征选择方法进行降维,从384维降至50维,即将算法中的选择特征最大个数s设置为50;②为了进一步降低特征向量的维数,并保证人体行为识别的准确率,实验通过遗传算法对第1步获取的50维特征子集进一步优化。遗传算法的种群规模取值为20,最大进化代数为50,采用适应值比例选择方法选择产生下一代种群个体,交叉概率设置为0.8,变异概率为0.01。实验运行10次后,取平均值作为结果。 接着,为了方便对比实验结果,实验将通过SVM分类器和KNN分类器分别进行分类。由于SVM分类器能有效解决非线性、小样本、维数灾难和“过学习”等分类问题,常见的核函数包括有线性核函数、多项式核函数和径向基核函数等,设有H种不同分类行为,则共需要P=H(H-1)/2个2类分类器。本实验采用的SVM模型选用径向基核函数,表示为 K(x,xi)=exp(-γ|x-xi|2) (11) (11)式中,参数γ=1/H,本文中有7种分类行为,因此实验中H的值设为7。 KNN分类器的基本工作原理是根据计算出的待分类样本x与所有训练样本间的距离,并从中选出x的k个近邻,然后统计这k个近邻的类别,并将x归入k个近邻中得票最多的那一类。根据经验规则,k一般小于训练样本数的平方根,因此本实验将k的值设为12。 为了体现本文方法相比其他方法的优势,本文将通过2方面对其进行比较:最终获取的特征个数和实验的分类性能。表2为3种不同行为混淆矩阵的举例说明。相应的,本文将通过识别准确率衡量本方法的分类性能。 表2 混淆矩阵举例表 Accuracy即平均识别准确率,表示每个测试样本被正确分类的可能性,即所有分类行为的平均识别准确率,其计算公式如(12)式所示 (12) 在实验中,通过本文提出的方法对7种常见人体行为提取的特征集进行降维,并分别采用SVM分类器和KNN分类器进行分类,实验采用留一交叉法检测得到的混淆矩阵及分类识别准确率分别如表3、表4所示。 表3 通过SVM获取的混淆矩阵及识别准确率Tab.3 Confusion matrix and recognition accuracy obtained by SVM 表4 通过KNN获取的混淆矩阵及识别准确率Tab.4 Confusion matrix and recognition accuracy obtained by KNN 从表3和表4的混淆矩阵及各行为识别精度可以看出,本文方法对实验分类的7种行为实现较高识别准确率,SVM分类器的平均识别正确率达到了97.02%,而通过KNN分类器也达到了95.73%;另外,从混淆矩阵可以看出,对2种易分类的静止行为(站立、躺卧)没有出现混淆,达到了100%的识别准确率,而对于容易混淆的步行、上楼和下楼3种行为,本方法通过SVM和KNN也分别达到了96.53%和92.59%的高识别精度,3种行为之间也只有较少测试样本发生了混淆。 为了进一步验证本文方法的有效性,实验将本文方法分别与另外4种特征选择方法进行对比,包括未使用特征选择方法、mRmR方法、文献[14]及文献[15],其中,文献[14]采用基于遗传算法优化的不一致相关度量方法,文献[15]采用主成分分析(PCA)和基于遗传算法优化的线性鉴别(LDA)相结合的特征选择方法,4种方法都选用SVM分类器和KNN分类器进行分类测试,其中SVM和KNN分类器中参数设置都保持相同,文献[14]、[15]中使用的遗传算法的设置参数也与本文方法保持一样,实验从分类精度及特征维数降低幅度2方面进行对比,实验结果如表5、表6、表7及图4和图5,其中,表5和表6为本文方法与其他4种方法通过SVM和KNN分类识别的各行为分类精度,图4和图5分别为不同方法在通过SVM和KNN分类器分类时获取的平均识别准确率,表7为5种方法通过2不同分类器筛选出的特征维数。 表5 不同特征选择方法通过SVM获取的总体识别精度Tab.5 Total recognition accuracy of different feature selection methods by SVM % 表6 不同特征选择方法通过KNN分类的各行为识别精度Tab.6 Total recognition accuracy of differentfeature selection methods by KNN % 表7 不同方法降维后的特征维数Tab.7 Feature dimensions of differentmethods after dimensional reduction 图4 不同方法通过SVM的总体平均识别准确率Fig.4 Total average recognition accuracyof different methods by SVM 图5 不同方法通过KNN的总体平均识别准确率Fig.5 Total average recognition accuracyof different methods by KNN 结合表5、表6及图4、图5的实验结果可以看出,与另外4种方法相比,从分类精度看,本文提出的方法有最高的平均识别准确率,SVM分类器达到了97.02%,KNN分类器也达到了95.73%,与不使用特征选择方法相比较,平均识别准确分别提高了15.92%和14.63%;与传统的mRmR方法相比较,也分别提高了13.72%和9.92%;与文献[14]、文献[15]对2种传统方法的改进方法比较,通过SVM分类器分类,分别提高了3.31%与1.76%,通过KNN分类,则分别提高了6.15%和3.37%。从图4、图5还可以看出,当不选用特征选择方法,直接进行分类时识别准确率最差,平均识别准确率只有81.10%,所以从侧面也体现出在一些行为分类中,随着提取特征维数的增加,特征选择方法在分类识别中的重要性。从表7的实验结果可以看出,当使用本文提出的特征选择方法,通过SVM分类时特征向量的维数从384维降到了37维,虽然高于另外2种方法降维后的特征维数,即文献[14]的19维和文献[15]的23维,但本文方法的识别准确率却高于文献[14]、文献[15]的方法,由此,也可以看出特征维数并非降的越低越好。而通过KNN分类时,特征维数降到了26维,比其他几种方法所获取的特征维数都要低,且获得最好的识别准确率。另外,与经典的mRmR的特征选择方法相比,本文方法也效果明显,从侧面也可以看出使用多种相关系数融合的特征选择方法比仅使用单一的相关系数的效果好。 图6 本文方法与文献[14]、文献[15]方法通过SVM分类精度Fig.6 Classification accuracy of the proposed method andthe methods of literature [14], literature [15] by SVM 由于文献[14]、文献[15]及本文方法中都采用了遗传算法进行优化,所以实验进一步对此3种方法在分类精度及收敛速度2方面进行对比,实验通过SVM分类器分类时获取的实验结果如图6。 从图6的实验结果可以看出,相比于文献[14]和文献[15]中提出的特征选择方法,本文方法在迭代次数上也是最快实现收敛的,并且最终的识别精度也是最高的。 针对在基于加速度传感器人体行为识别的研究中,由于特征维数的增加会造成冗余,进而降低分类识别准确率的问题,本文提出一种基于遗传算法优化的多种相关系数融合的特征选择方法,该方法在基于mRmR准则下,通过多种相关系数融合的方法去除部分冗余、不相关特征,并利用遗传算法搜索最优或次优特征子集,通过与其他4种典型特征选择方法进行对比,实验分别采用SVM分类器和KNN分类器进行分类识别,结果表明:该方法具有优异的特征降维性能,同时对实验分类的7种不同人体行为实现更好的分类效果,平均识别准确率分别达到了97.02%和95.73%,与不使用特征选择方法相比较,平均识别准确分别提高了15.92%和14.63%;与传统的mRmR方法相比较,分别提高了13.72%和9.92%;与文献[14]、文献[15]对2种传统方法的改进方法相比较,通过SVM分类器分类,分别提高了3.31%与1.76%,通过KNN分类,则分别提高了6.15%和3.37%。在收敛速度方面,相比于文献[14]和文献[15]中提出的特征选择方法,本文方法在迭代次数上也是最快实现收敛的,并且最终的识别精度也是最好的。通过本文方法及实验结果可以发现,有效地利用多种相关度量方法不仅可以起到较好的特征选择作用,而且对实验的平均识别准确率也有显著提高。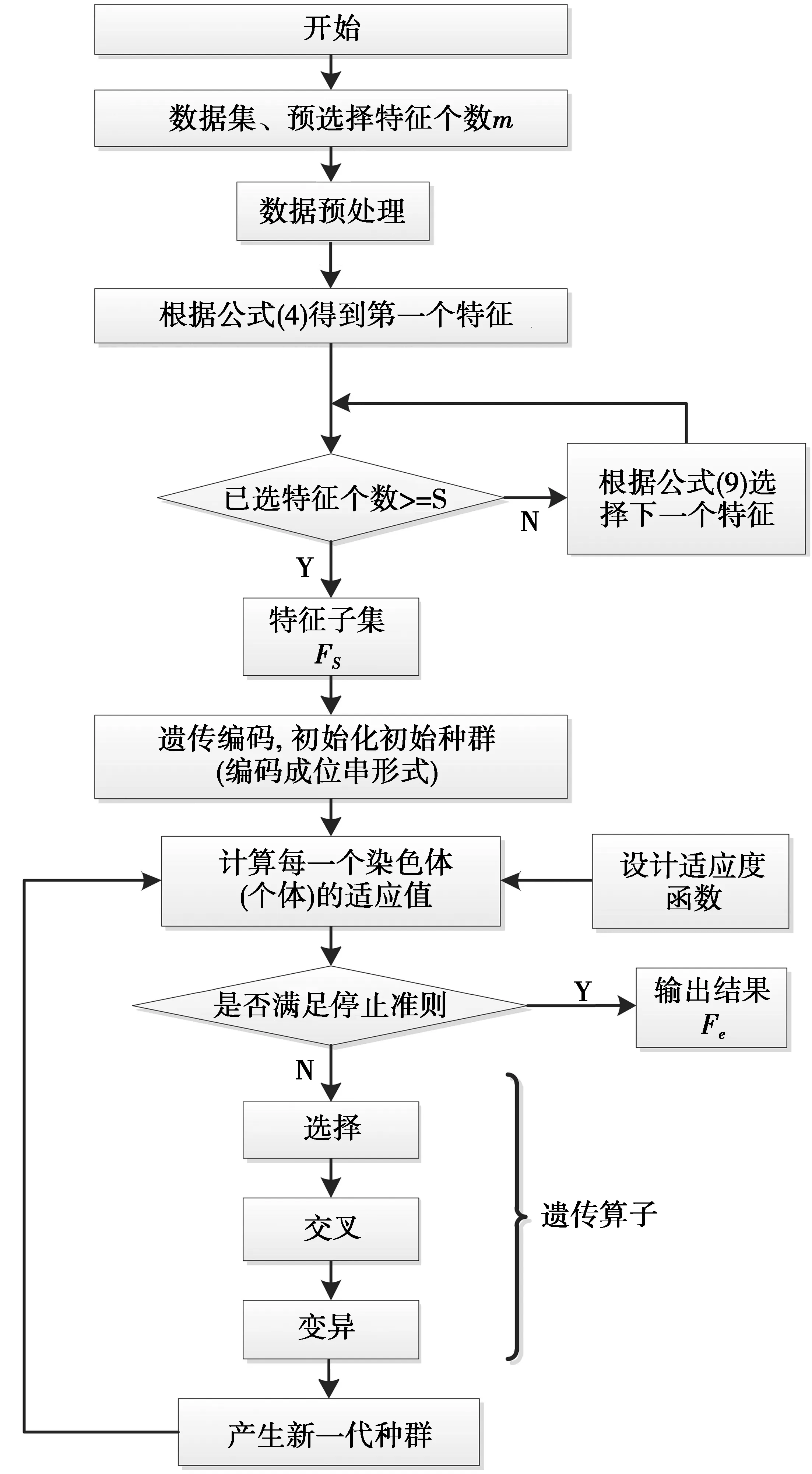
3 实验设计与结果分析
3.1 实验数据集

3.2 实验设置


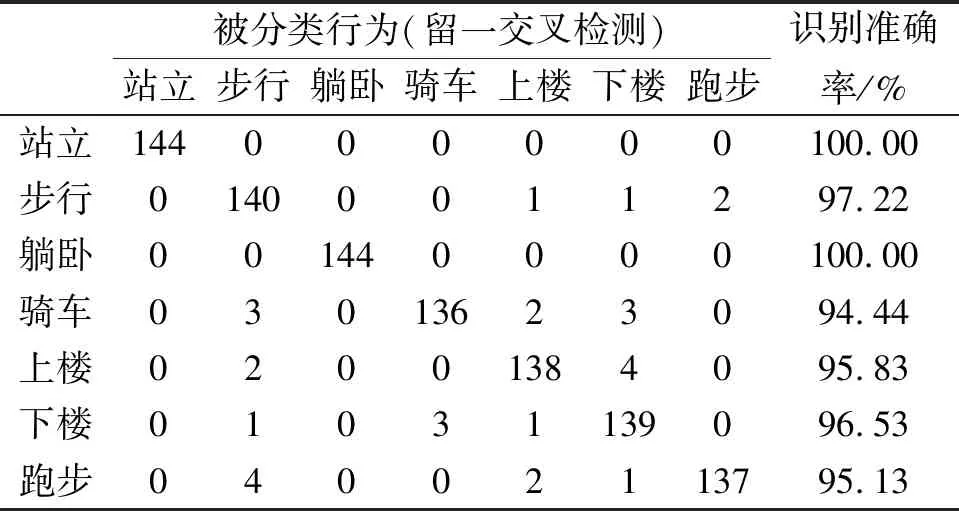
3.3 实验性能测量方法

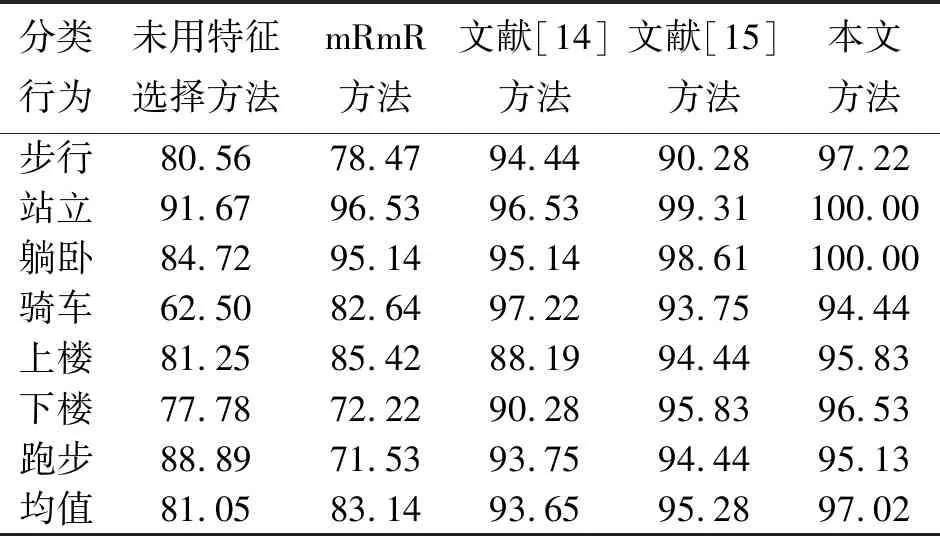
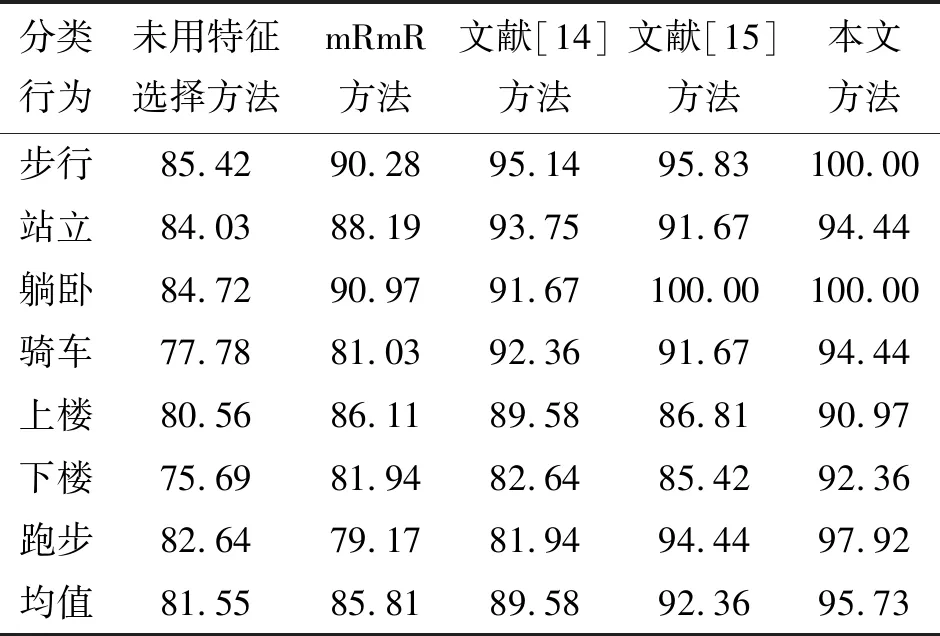
3.4 实验结果与分析

4 结束语

