脉冲噪声单脉冲分析及建模

黄 琼，龚 航，王 毅,,4，李松浓，郑 可，孙洪亮

(1.重庆邮电大学 理学院，重庆 400065；2.重庆邮电大学 通信与信息工程学院，重庆 400065；3.国网重庆市电力公司 电力科学研究院，重庆 400014；4.国网重庆市电力公司 博士后科研工作站, 重庆 400014)

0 引 言

电力线通信(power line communication，PLC)是指利用电力线网络进行数据、语音、图像传输的一种通信方式。电力线通信存在用户多、分布广、投资少、不需要重新布线、运行成本低、使用简便等优势。近年来，电力线通信快速发展，传输速率大幅提高，成为解决宽带网络瓶颈——“最后一公里”的新的接入技术。但电力线的设计最初是为了传输电能，而不是通信，因此，电力线通信环境并不理想。噪声、衰减、阻抗是影响电力线信道传输的主要因素，且随时间、频率、地点的变化而变化，严重影响电力线通信质量和速率，是研究电力线通信的难点[1-2]。为了提高低压电力线的通信性能，有必要对电力线信道噪声特性进行研究。

噪声通常分为背景噪声和脉冲噪声，其中，脉冲噪声是影响通信质量最主要的因素。电力线中的脉冲噪声主要是由电路中负载电器的开关通断以及插座中插头的插拔引起。对于电力线通信系统中的脉冲噪声，Bernoulli-Gaussian(BG)，Middleton’s Class A模型都能较好地建模[3-5]。但是这些模型认为脉冲噪声内部的脉冲点是相互独立的。在实际中，突发噪声内部的脉冲点不仅具有依赖性而且还具有相关性，不同的噪声源可能导致很大的脉冲方差。

Zimmermann和Dostert发现脉冲噪声有时以突发状态出现，即每一个脉冲长度内存在若干个脉冲噪声点，说明该噪声具有记忆性[6]。Gilbert-Elliot模型能简单建模随机脉冲噪声[7-8]，该方法可以用2个状态建模脉冲(误差)事件的脉冲间隔和脉冲宽度。考虑到脉冲噪声是随机事件，其特性可以用随机变量表示，文献[9]提出基于分群马尔科夫链(Markov chain, MC)的噪声统计模型。之后，其他作者研究了具有记忆的脉冲噪声[10-15]。在文献[11]中，用一个2级的两状态MC描述突发性脉冲噪声。第1级用一个两状态的一阶MC描述脉冲噪声的出现，第2级用另一个两状态的一阶MC描述该突发性脉冲噪声的内部特性。描述有记忆的脉冲噪声方法是在描述无记忆的脉冲噪声方法基础上发展而来的，比如Class A模型和Bernoulli-Gaussian模型与MC结合，分别得到了Markov-Gaussian模型[12]和Markov-Middleton模型[13]。

本文通过实际测量家用电器在工作中产生的脉冲噪声，发现家用电器产生的噪声不仅具有突发态，而且还有一定的包络。具体表现为每个包络呈现相同阻尼衰减趋势，但整体的包络长度、包络幅值是随机变化，局部的波峰衰减幅度、波峰出现频率也是随机变化的。显然,现有的模型忽略了该包络特性。研究多组单脉冲噪声包络，发现该包络特性在频域上表示为多线段特性，通过波形的极值点能够拟合该波形。

本文提出了频域极值点模型建模脉冲噪声的单脉冲波形，利用MC建立频域极值点序列统计模型，得到的频域极值点序列拟合噪声实部和虚部频域波形，经快速傅里叶逆变换(inverse fast Fourier transform，IFFT)能够产生在时域上具备包络特性的单脉冲噪声。仿真结果表明，提出方法所构造的单脉冲波形不仅在统计规律上与真实噪声相同，而且在其突发性基础上展现良好的包络特性。

1 噪声测量及分析

1.1 测量方案

图1给出了一种经典的噪声测试方案。图1中，线路阻抗稳定网络(line impedance stabilization network，LISN)是电力系统电磁兼容测试中的一种重要设备，其功能类似于滤波器和稳压器。将LISN加在前端电力线网络和被测设备之间，可以最大限度地滤除从配电房内外其他仪器设备带入电力线中的噪声干扰，尽可能地还原出纯净的电力线网络供被测设备接入。同时，还可以尽量稳定电力线网络的阻抗，并提供一定的稳定电压，以便对电压比较敏感的仪器起到保护作用。而被测设备接入LISN经处理后的电力线上可使设备工作后产生的噪声馈入电力线内。然后，这些干扰信号，通过一个具有高通滤波功能的耦合器耦合到PicoScope仪器中。PicoScope仪器是釆集噪声的主要仪器，并可以大体观察噪声波形。釆集得到的噪声数据可以通过与PC本地保存为.mat文件，PC端可以直接对.mat文件进行读取和分析。

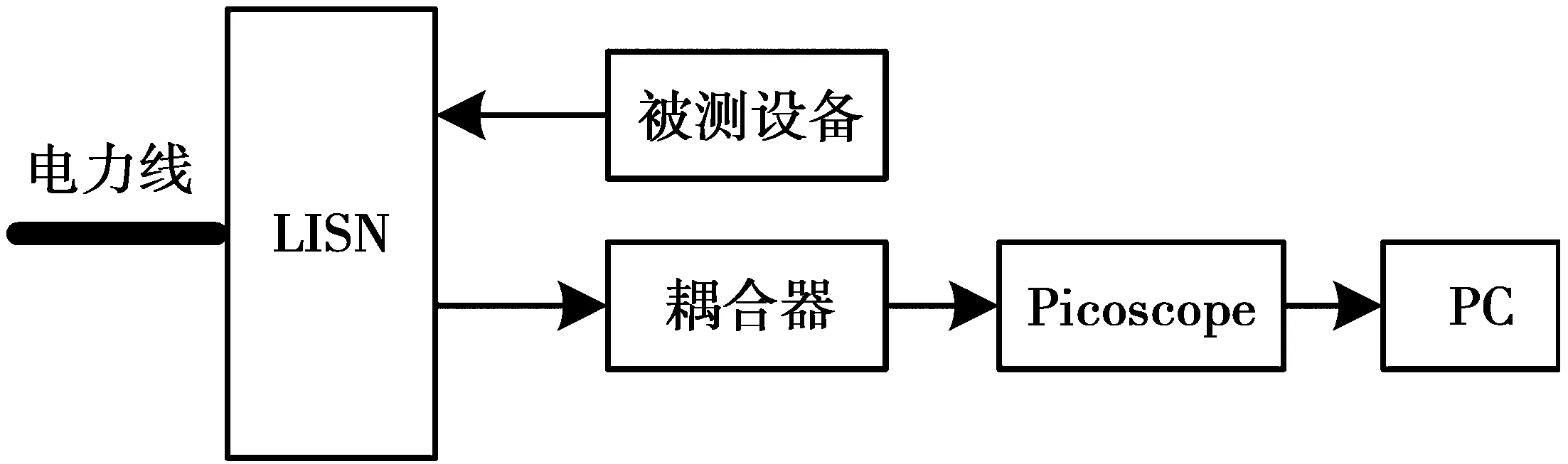
图1 噪声测试方案Fig.1 Scheme for measuring power line noise

本文取家用电器吹风机为研究对象，PicoScope数字示波器设置采样周期为16 ns，采样频率为62.5 MHz，测量了20组电力线通信信道噪声，图2为某一组测试噪声局部波形。

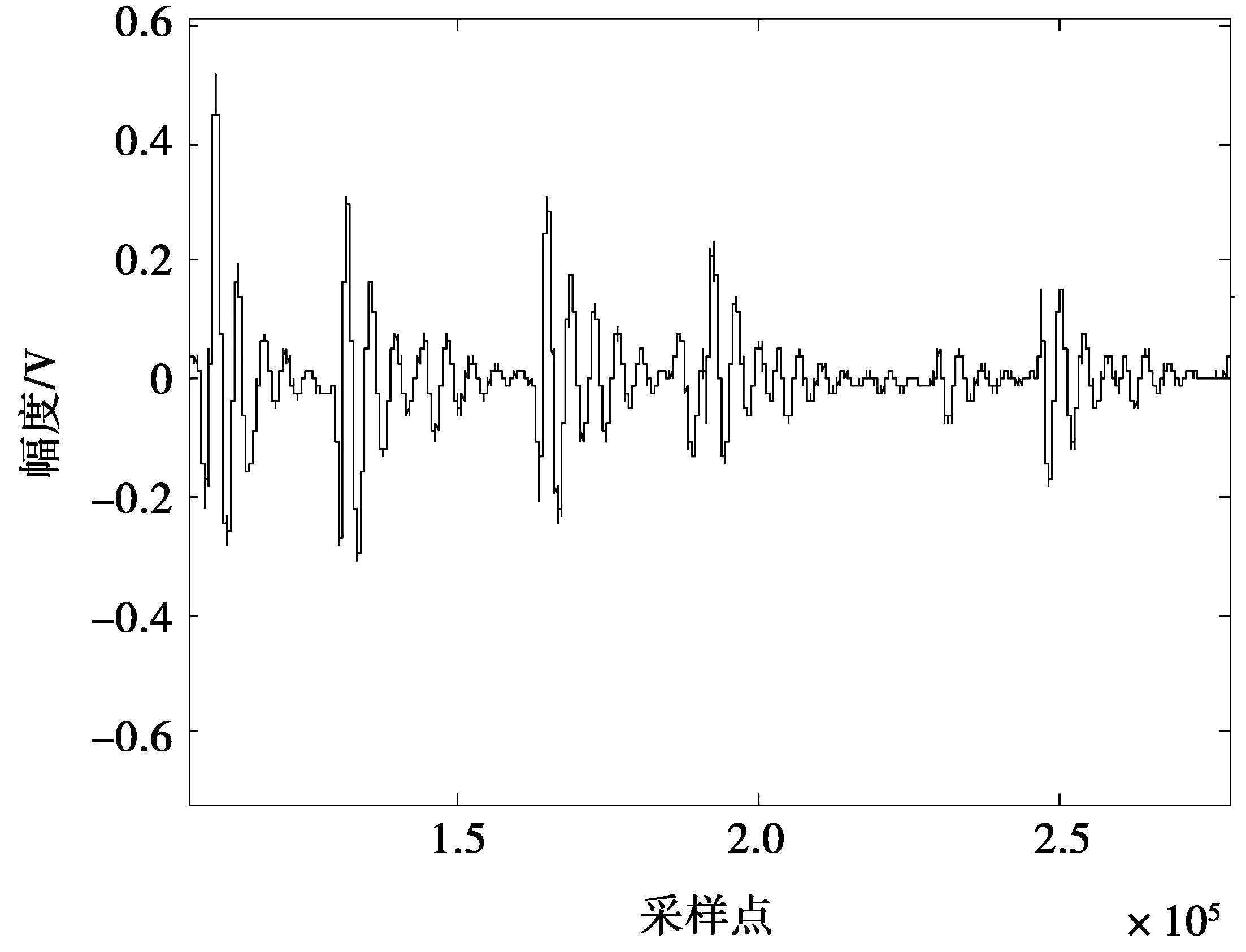
图2 一组实测电力线噪声的局部波形Fig.2 One group of measured part of power line noise

1.2 测试结果分析

噪声在其脉冲宽度范围内不是以单点脉冲存在，而是连续出现，也就是说该噪声呈现一种突发状态，称之为突发噪声。从家用电器吹风机工作时产生的局部噪声波形(见图2)，可以看出，该组噪声呈现突发状态，符合突发噪声的定义。

2 马尔科夫链理论

马尔科夫过程是目前发展很快、应用十分广泛的一类重要的随机过程，由马尔科夫链定义可知，一个状态和时间参量都是离散的随机过程X(n)，在k时刻状态X(k)已知的条件下，其后k+1时刻所处的状态只与k时刻的状态有关，而与之前时刻的状态无关；马尔科夫链的概率Pi,j(s,n)=P{xn=aj|xs=ai}为马尔科夫链在xs=ai的条件下，xn=aj的条件概率或转移概率，由转移概率构成的矩阵称为马尔科夫链的转移矩阵。

MC模型是基于有限时间的马尔科夫链理论，未来的状态只与当前有关，其过程的行为用状态表示。一个MC模型可表示为(S,P,Q)，其中，S是系统所有可能状态所组成的非空状态集，也称为系统的状态空间；P是系统状态转移概率矩阵；Q是系统初始概率分布。

3 脉冲噪声单脉冲模型

测量表明，脉冲噪声在其脉冲宽度范围内不仅是连续出现的，而且表现出一定的包络特性。文献[12]提出了有记忆的脉冲噪声模型Markov-Middleton，它结合Middleton Class A和Markov模型，Middleton Class A模型可以建模从纯高斯分布噪声到任意脉冲噪声特性的噪声，加入Markov模型使之具有突发性。图3为Markov-Middleton模型参数A=0.2,Γ=0.01,x=0.98,σ2=1的噪声仿真，其中，A为冲击指数，为单位时间内接受的平均脉冲数与脉冲持续时间的乘积；Γ为高斯噪声分量的平均功率与冲击噪声分量的平均功率的比率；x为决定噪声样本之间相关性的概率；σ2为总噪声功率。由图3可知，该噪声中脉冲的产生呈现泊松分布，在脉冲宽度范围内噪声连续出现，表现出很好的突发特性，然而该模型忽略了其包络特性，无法将包络形态表现出来。针对脉冲噪声的包络特性问题，本文提出了单脉冲建模方法。

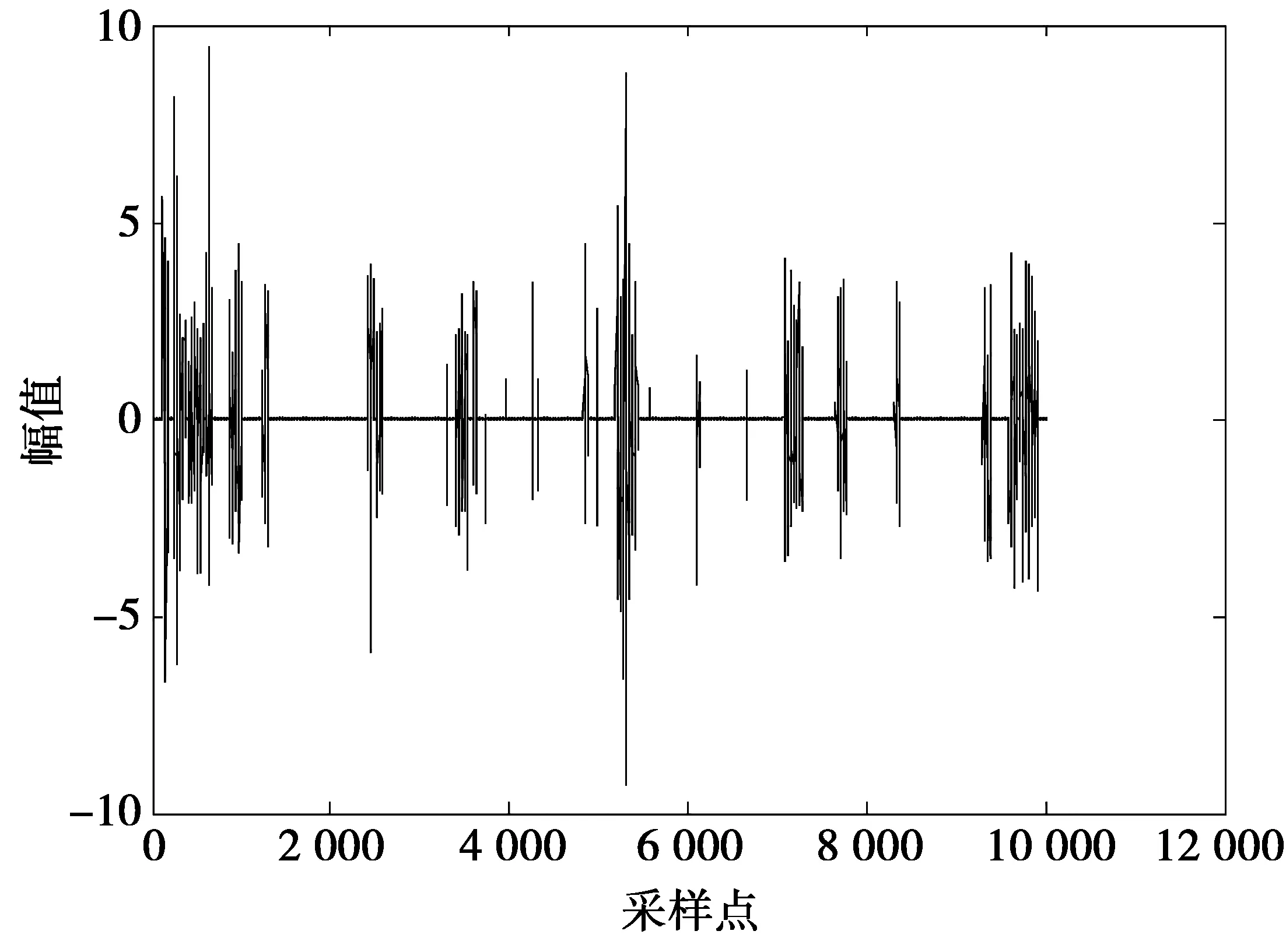
图3 Markov-Middleton模型参数的噪声实现Fig.3 Noise realization of the Markov-Middleton model with

3.1 单脉冲模型分析

实测483组单脉冲时域波形样本，采样频率为62.5 MHz。从频域观察发现噪声主要集中在0～100 kHz频段，如图4所示。因此，主要对该频段范围内的采样点进行分析。分析发现，单脉冲的包络特性在频域上均表现为多线段特性，从整体上可以看作分段线性曲线，由多个波峰和波谷组成。采用波形的极值点作为分段曲线的断点，通过极值点重新拟合该频域波形。图5a展示一组实测和极值点拟合的单脉冲噪声样本在0～100 kHz频段的实部频域波形；图5b展示一组实测和极值点拟合的单脉冲噪声样本在0～100 kHz频段的虚部频域波形。图5中，极值点拟合的频域波形显示，极值点拟合与实测产生的频域波形基本一致，频域取极值点所拟合的波形能够很好地表示单脉冲频域特征。图6展示了极值点拟合的实部和虚部频域波形所构造时域波形。结果显示，极值点根据频域特性拟合的频域实部和虚部波形，经IFFT变换后表现出了良好的包络特性。

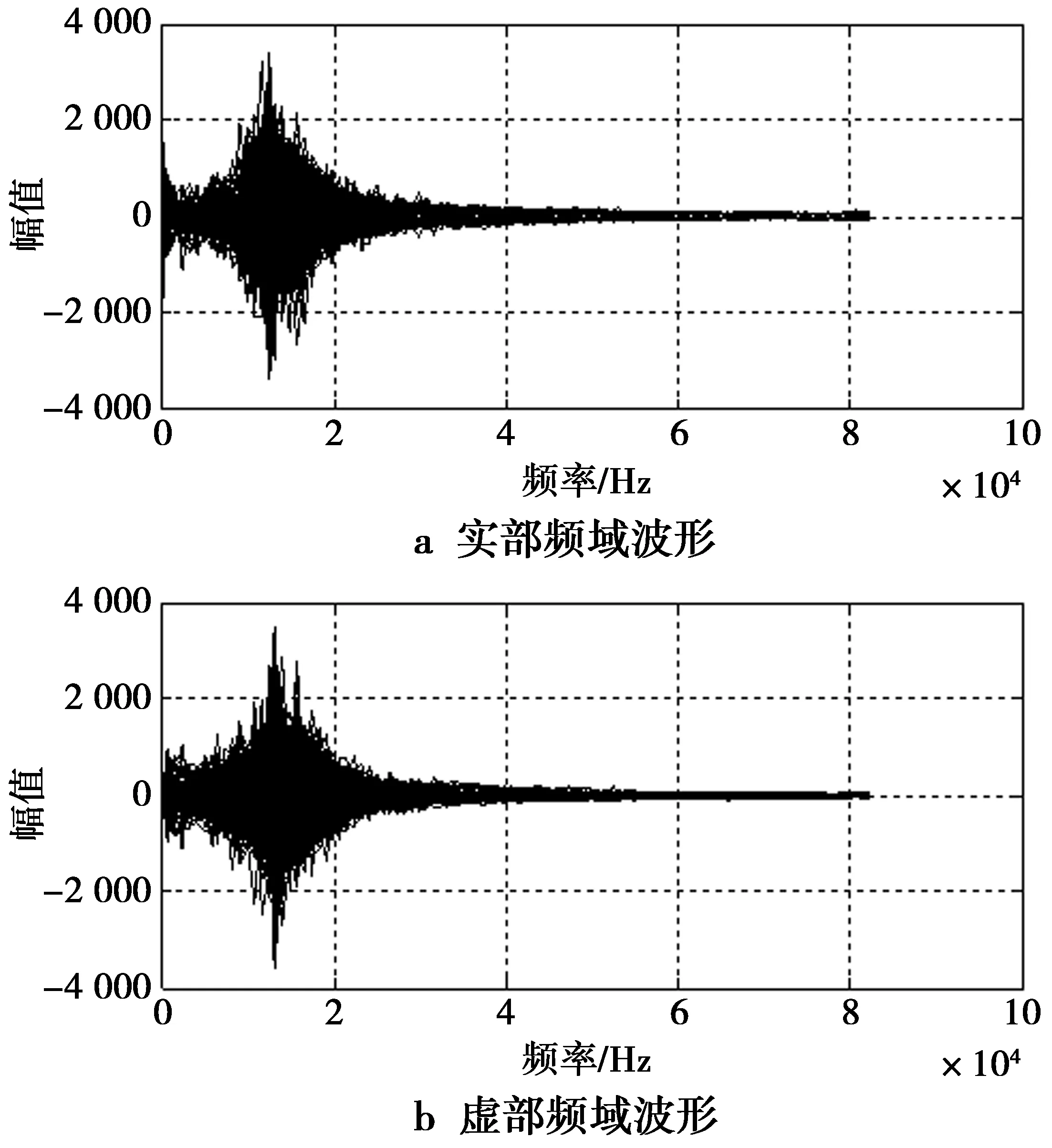
图4 频率在0～100 kHz的483组单脉冲频域波形Fig.4 483 groups of single-pulse frequency-domainwaveforms in the frequency band 0～100 kHz

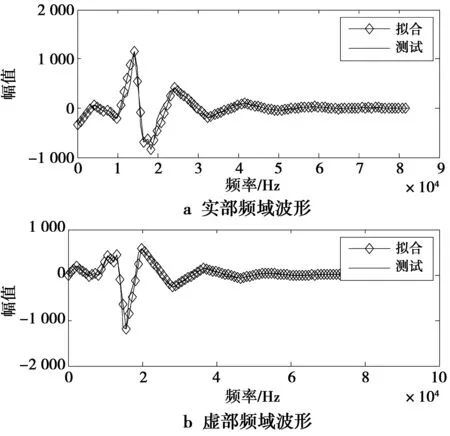
图5 实测和极值点拟合的单脉冲噪声样本在0～100 kHz的频域波形Fig.5 One group of frequency-domain waveforms ofmeasured and extreme point fitting single-pulse noise samples in the 0～100 kHz band

图7a和图7b分别展示频域实部和虚部的4组极值点序列。极值点由频率和幅值唯一确定，根据频率和幅值的大小，可以将极值点划分为不同的状态。观察发现每组频域极值点序列都不相同，具体表现为幅值维度上状态在高低状态之间转变，频率维度上状态从低状态向高状态转变。χ2检验方法能够检验离散的状态序列是否具有马尔可夫模型的性质[16]。通过该方法统计计算发现，极值点状态序列为马尔可夫链，本文可以利用马尔可夫链模型统计建模极值点序列。

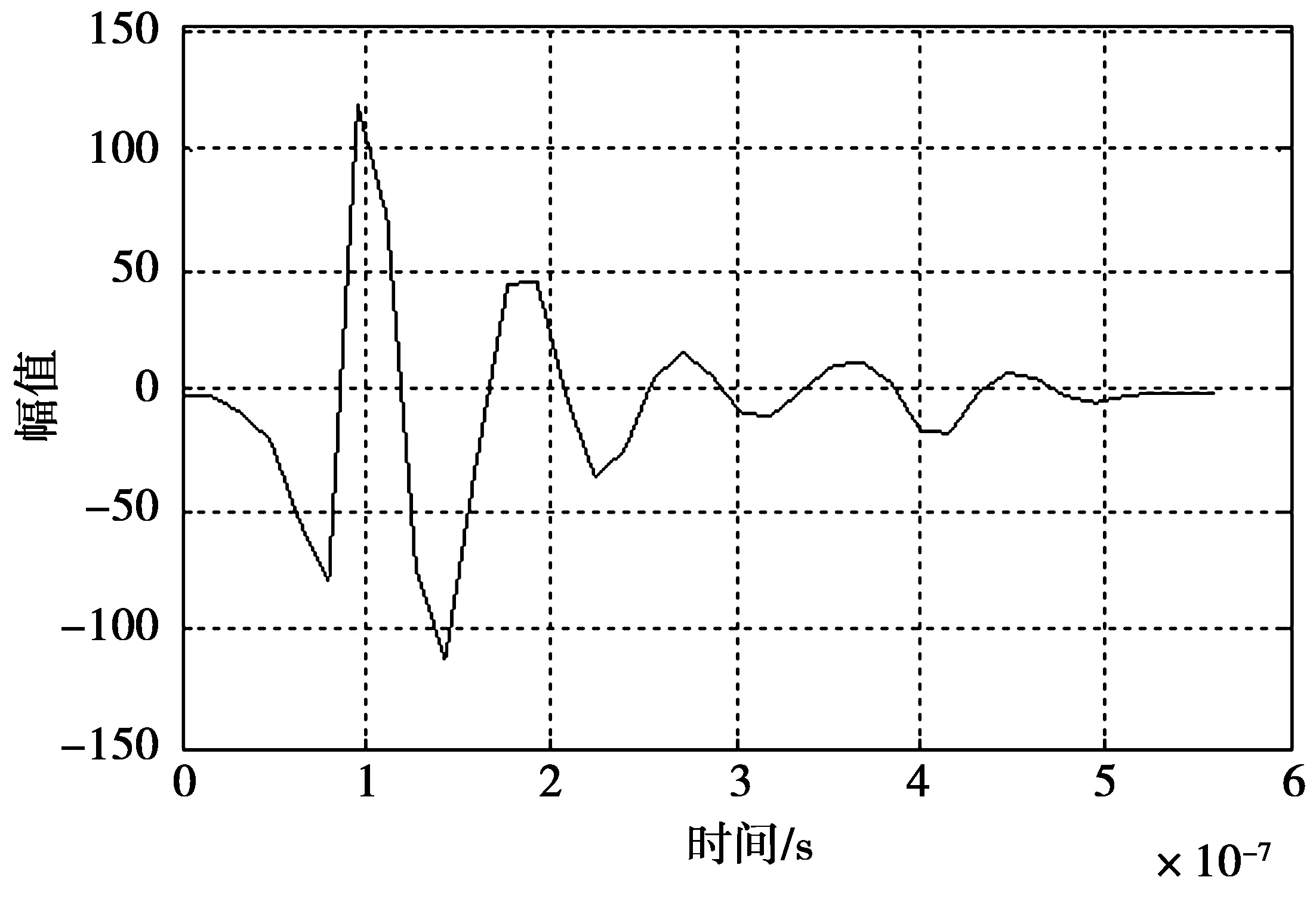
图6 一组极值点序列构造的单脉冲波形Fig.6 A group of single pulse waveforms constructed by extremum point sequence

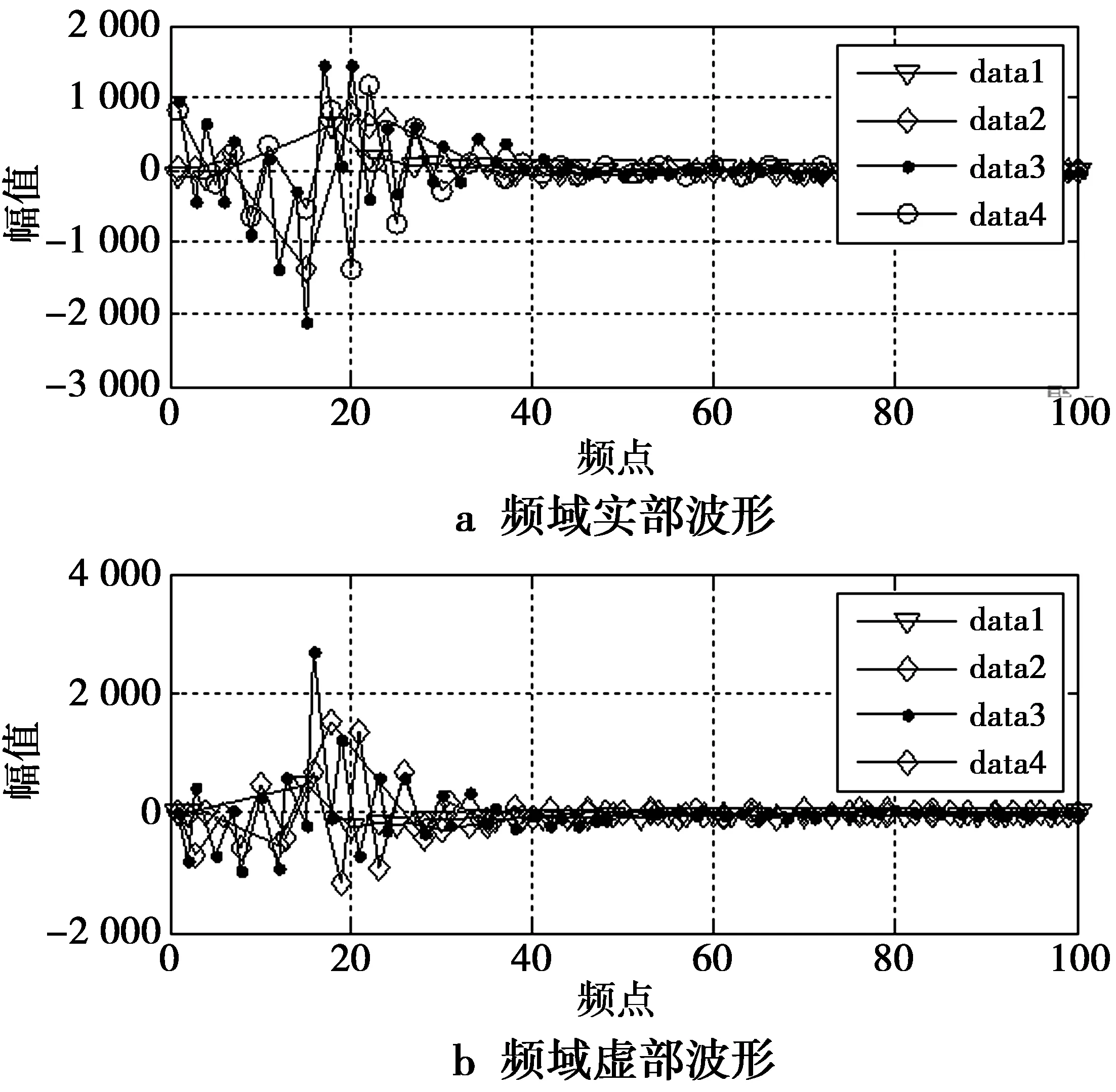
图7 4组频域极值点序列Fig.7 4 groups of frequency domain extreme point sequence

3.2 马尔科夫建模极值点序列

马尔科夫模型主要由3个参数表示，分别是状态空间、状态转移矩阵和初始状态分布矩阵。建模频域极值点由以下步骤实现。

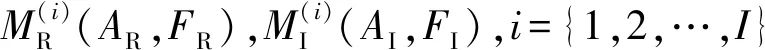
2)状态空间确定。已知AR，AI，FR，FI序列，可以确定频率和幅值的状态空间。m，n分别表示频率和幅值的状态空间容量。根据幅值和频率大小的不同，m取值100，n取值50。实部和虚部的幅值状态空间分别表示为

XR={AR,1,AR,2,…,AR,m}

(1)

XI={AI,1,AI,2,…,AI,m}

(2)

(1)—(2)式中：AR,m，AI,m分别为实部和虚部的第m个幅值状态。

实部和虚部的频率状态空间分别表示为

YR={FR,1,FR,2,…,FR,n}

(3)

YI={FI,1,FI,2,…,FI,n}

(4)

(3)—(4)式中：FR,n，FI,n分别为实部和虚部的第n个频率状态。

频域上的每个极值点都是由频率和幅值唯一确定，因此，极值点状态空间可以表示为

ZR={[AR,i,FR,j],i=1,2,…,m;j=1,2,…,n}

(5)

ZI={[AI,i,FI,j],i=1,2,…,m,j=1,2,…,n}

(6)

(5)—(6)式中，状态空间容量为m×n。

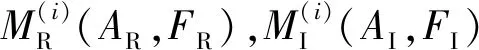
(7)

(8)

(7)—(8)式中，pi,j(i=1,2,…,m×n,j=1,2,…,m×n)表示状态i转移为状态j的概率。

QR=[p1,p2,…,pm×n]

(9)

QI=[p1,p2,…,pm×n]

(10)

(9)—(10)中，初始状态分布概率Pi(i=1,2,…,m×n)表示初始时刻状态i的概率。

5)产生极值点序列。根据马尔科夫链模型，已知模型的状态空间、初始分布概率矩阵及状态转移概率矩阵，可以仿真出无数组频域极值点序列。

4 仿真结果验证

实测483组单脉冲噪声样本，根据样本统计计算分别得到实部和虚部极值点的状态转移概率矩阵PR，PI，初始分布概率矩阵QR，QI及状态空间Z1，Z2。利用马尔科夫链模型建模极值点，可以得到无数组频域实部和虚部的极值点序列。模型构造的频域极值点概率密度和测试的频域极值点概率密度如图8和图9所示。从图8中可知，模型产生的频域极值点频点和测试的频域极值点频点概率密度曲线基本吻合。从图9中可知，模型产生的频域极值点幅值和测试的频域极值点幅值概率曲线也基本吻合。计算其均方根误差，均在0.02以下。因此，本文所提的马尔科夫链模型能够准确地模拟频域极值点序列。

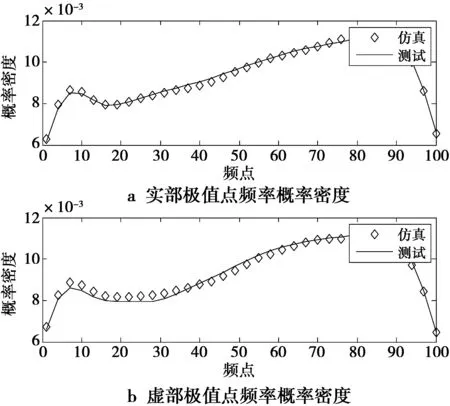
图8 仿真生成和测试生成的频域极值点频点的概率密度函数比较Fig.8 Comparison of probability density functions forfrequency point of frequency domain extreme pointbetween simulation and measure

通过其中4组实部和虚部的极值点序列拟合，构造了4组单脉冲序列如图10所示。该方法所构造的时域波形不仅具有良好的突发状态，而且表现出了一定的包络特性，每个包络呈现相同阻尼衰减趋势，但整体的包络长度、包络幅值是随机变化，局部的波峰衰减幅度、波峰出现频率也是随机变化的。验证了该方法的可行性。

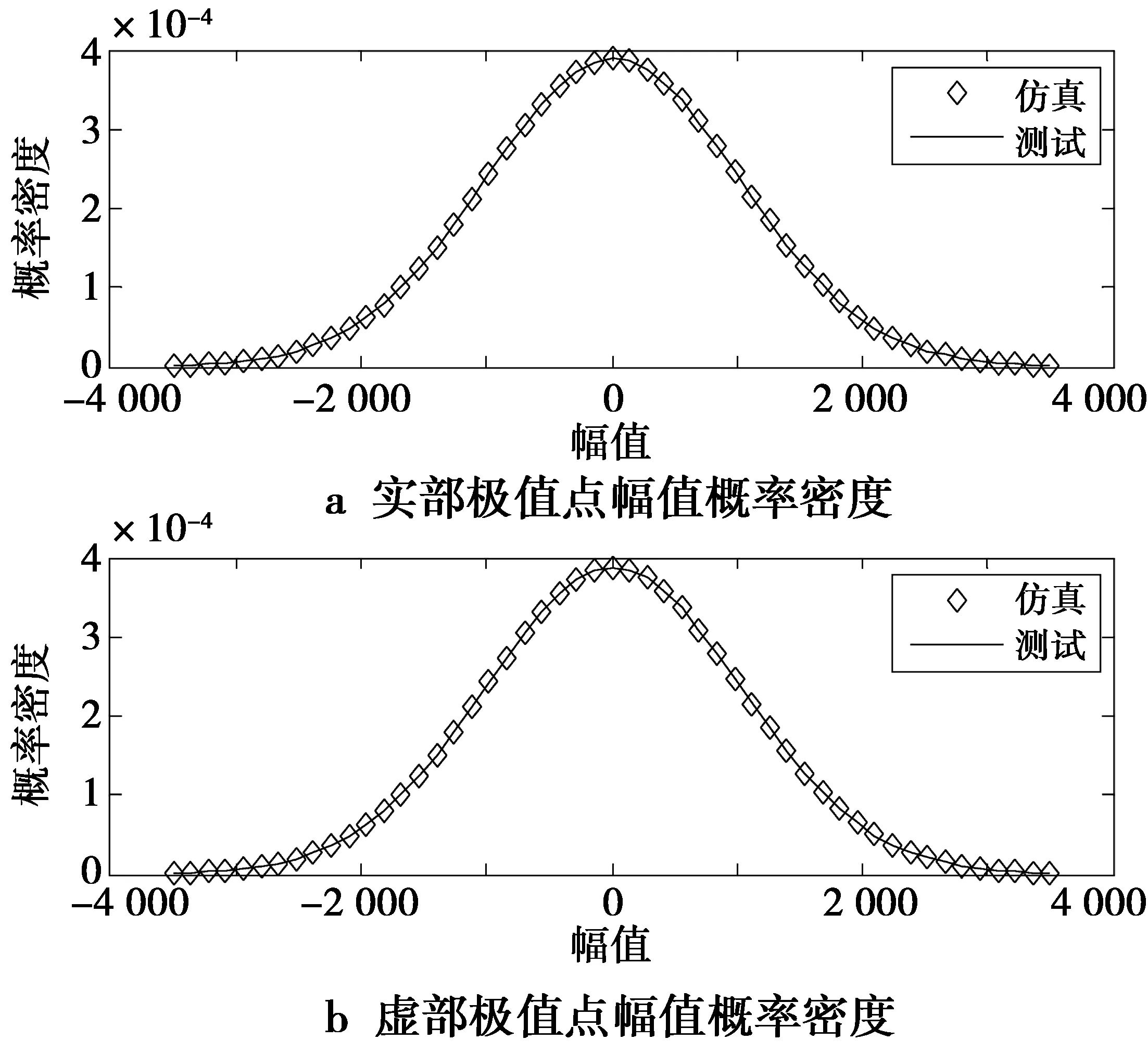
图9 仿真生成和测试生成的频域极值点幅值的概率密度函数比较Fig.9 Comparison of probability density functions foramplitude of frequency domain extreme point betweensimulation and measure

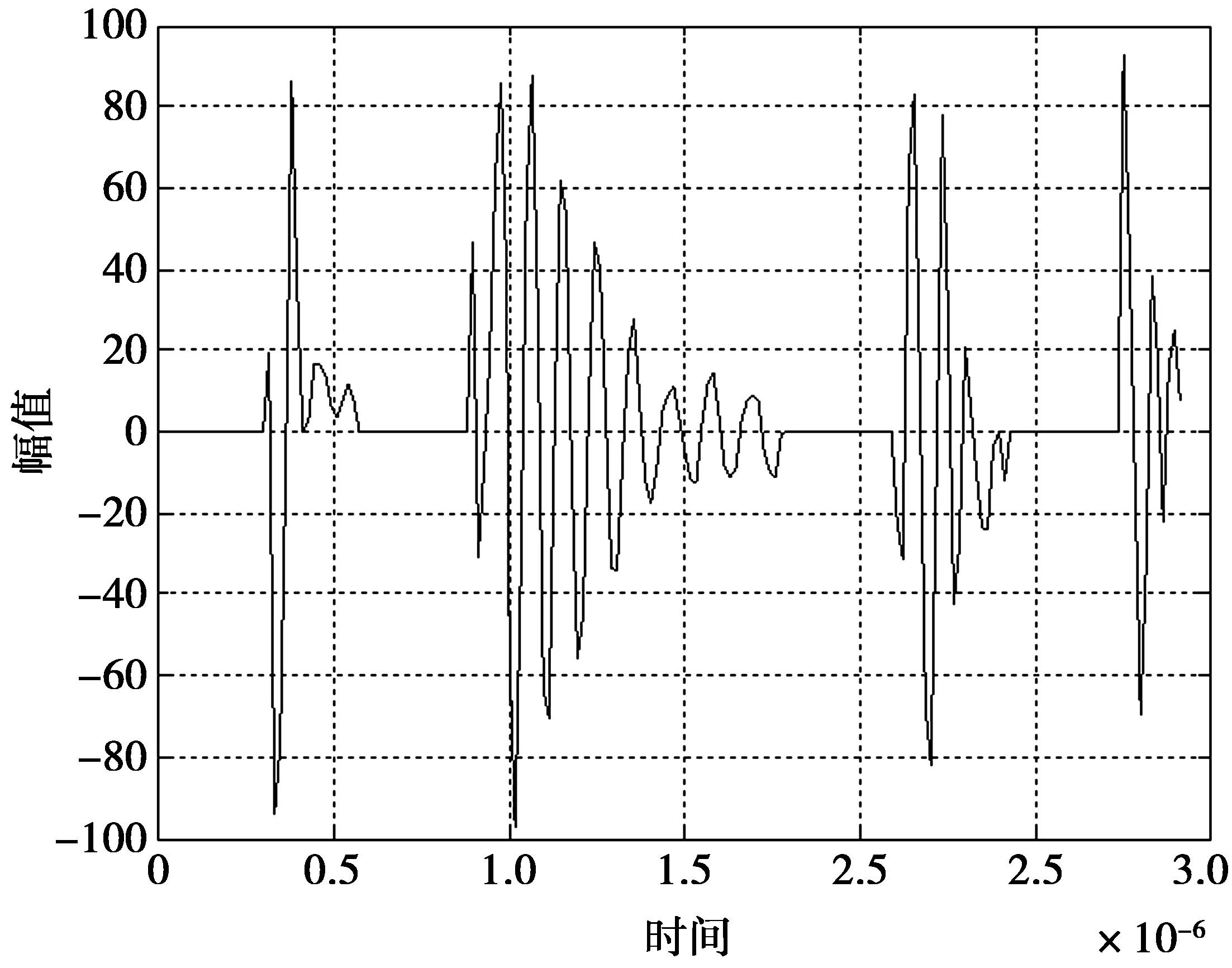
图10 本文建模方法构造的4组单脉冲波形Fig.10 4 groups of single pulse waveforms constructed by proposed model

5 结束语

脉冲噪声是影响电力线通信的主要因素。实测发现，脉冲噪声具有2个特性：①突发性，在其脉冲宽度范围内噪声并不是以单点脉冲存在，而是连续出现；②包络性，具体表现为每个包络呈现相同阻尼衰减趋势，但整体的包络长度、幅值是随机变化的，局部的波峰衰减幅度、波峰出现频率也是随机变化的。针对该特性，提出了频域极值点模型来建模单脉冲波形。通过仿真验证，提出的模型不仅考虑了脉冲噪声的突发性，更重要的是将脉冲的包络性也表现出来。为进一步进行电力线通信信道脉冲噪声建模提供了切实可行的方案。