基于筛选法的球载雷达解距离模糊改进方法
张小涵,刘润华,汪 枫,宿文涛
(空军预警学院,武汉 430019)
0 引 言
在脉冲多普勒雷达中,常常会遇到求解速度模糊和距离模糊的问题。脉冲多普勒雷达低重复频率(LPRF)有速度模糊而无距离模糊,中重复频率(MPRF)既有速度模糊又有距离模糊,而高重复频率(HPRF)一般只出现距离模糊[1-2]。球载雷达在中重复频率模式下工作,同时存在速度模糊和距离模糊。本文中的目标为接近气象杂波的慢速目标,目标移动引起的多普勒频率远远小于雷达发射脉冲的重复频率,不会产生速度模糊,因此本文重点考虑解距离模糊问题。对于解距离模糊,雷达目前最常用的是多重PRF的工作方式[3],常用的方法有孙子定理法[4-5]、余差查表法[6]和一维集法[7]等,这3种算法的原理是中国余数定理,且PRF选取方法一致[8]。这几种算法各有优点和不足,适合不同的解模糊情况[9]。
文献[4]提出的孙子定理法计算简便且算法复杂度低,但是对于距离测量的准确性和重频的选择要求很高[10];而文献[7]提出的一维聚类算法具有良好的误差纠错能力,既适用于解距离模糊,又适用于解速度模糊,但它的计算量太大,无法满足实时性的要求。文献[8]主要研究了余差查表法解单目标距离模糊问题。上述这些方法的缺点在于对噪声和距离量化误差比较敏感,在量测精度不高和信噪比较低时难以正确解距离模糊[11]。关于多目标解模糊问题,文献[12, 13]研究了多目标解模糊问题,但是均是在目标回波正确配对的情况下进行研究,没有考虑不同重频下目标与回波的失配问题。文献[14]提出了一种在距离、速度维联合解模糊的算法,但本文的目标运动速度较慢,且速度变化范围较小,不足以在球载雷达工作重频上构成速度模糊,因此该方法并不适用。文献[15]提出的筛选法虽然不用目标与回波正确配对就可以解模糊,但是不能解决目标在同一重频视在距离重合的问题。本文采用一种筛选法改进方法,该方法不仅可以快速解模糊,还可以解决目标同一重频视在距离重合的问题,且有较好的容错性。
1 传统解模糊算法
设有n种重频解距离模糊,各重复频率对应的最大不模糊距离分别是Ru1,Ru2,…Run,雷达需要探测的最大距离是Rmax。目标在各个重复频率上的视在距离分别是R1,R2…Rn,如图1所示。距离模糊就是指同一个重频上的视在距离可以对应很多个目标实际距离。
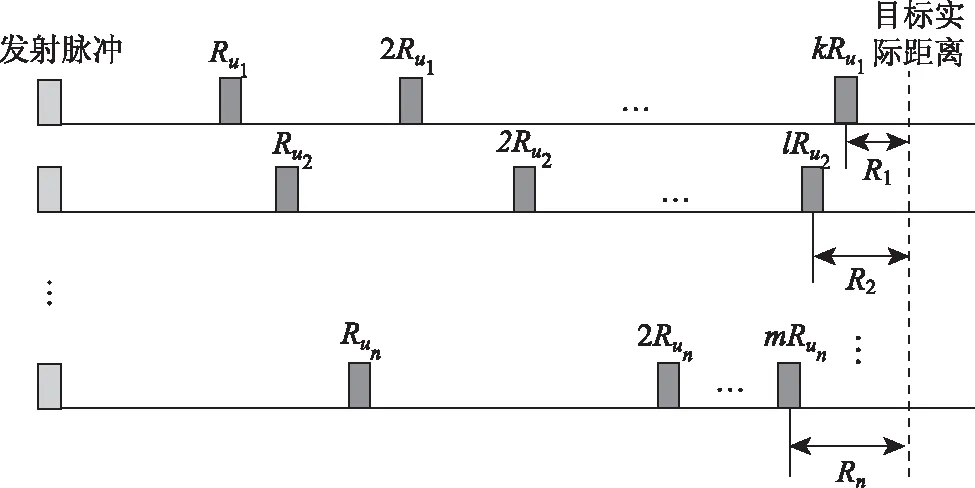
图1 视在距离示意图
1.1 一维集算法
一维集算法首先列出每个重频上得到的目标的视在距离所对应的全部可能的距离值:
Rik=Rk+i*Ruk,i=1,2,…int(Rmax/Ruk)
(1)
其中,Rk是第k重复频率对应的视在距离,Ruk是第k重复频率对应的最大不模糊距离。将得到的全部距离按照从小到大的顺序排列, 并用式Roi表示。依次取n个距离值求它们的均值和方差,则其方差为
(2)

1.2 余差查表法
以四重频为例,根据图1可知
R=N1×Ru1+R1=N2×Ru2+R2=
N3×Ru3+R3=N4×Ru4+R4
(3)
其中,R是目标的真实距离,Nk是在第k重PRF下的模糊数;若当N1N2N3N4互质且均为最小时,求得的目标真实距离唯一。本文以第一重频为基准重频, 余差表存储的信息为R2,iR3,iR4,iN1,i。其中,下标i表示距离单元个数,表值Rk,i=rk-r1,k=2,3,4表示某一距离单元在各重频上的余数之差,表值N1,i为某一距离单元在第一重频上的模糊度大小。当已知一组PRF时,可以通过上述运算在余差表中查找余差查表法的解,得到第一重PRF对应的模糊度值N1,则最终求得的目标真实距离值为:
R=N1×Ru1+r1
(4)
余差查表法计算方法简便,解算准确,有很强的解模糊能力。但是当某一重频目标视在距离重合时,不能进行准确解算。余差查表法在测距范围不大时能够快速匹配出目标的真实距离,但随着目标的测距范围增大其时间复杂度和空间复杂度都会迅速增加[8],且对每个驻留时间内检测到目标的帧数有较高的要求[16]。
1.3 筛选法
筛选法的思想是先选定一个重频作为基准重频, 把基准重频测距时得到的视在距离Ri对应的所有可能的真实距离一一列出,得到一个含有目标真实距离的集合,再以其它重频的视在距离作为检验项判断集合里的各个元素, 直到从集合中筛选出真实目标。
筛选法的具体实现过程为:
(1)求出目标在第k重复频率上的视在距离所对应的所有可能距离Xi,组成一个集合
x={X1,X2,X3,X4…Xm}
(5)
其中Xi=(Rk+ΔR)+i*Ruk,ΔR表示雷达测距误差,i=1,2,…m为模糊数,m=int(Rmax/Ruk)为最大模糊度。
(2)按顺序取出集合x中的元素,对剩余的其他重频对应的最大不模糊距离Ruk取余,得到一组余值为
di={XimodRu1,XimodRu2,…XimodRuk-1,
XimodRuk+1,…XimodRun}
(6)
(3)视在距离组成的向量为
r={R1+ΔR,R2+ΔR,…Rk-1+ΔR,
Rk+1+ΔR,…Rn+ΔR}
(7)
将得到的各个di与该向量相减,得到差值向量
ei=di-r={Ei1,…Ei(k-1),Ei(k+1),…Ein}
(8)
其中Eij=XimodRuj-(Rj+ΔR),j=1,2,…k-1,k+1,…n。
(4)对各ei取绝对值范数
‖ei‖=|Ei1|+…+|Ei(k-1)|+
|Ei(k+1)|+…+|Ein|
(9)
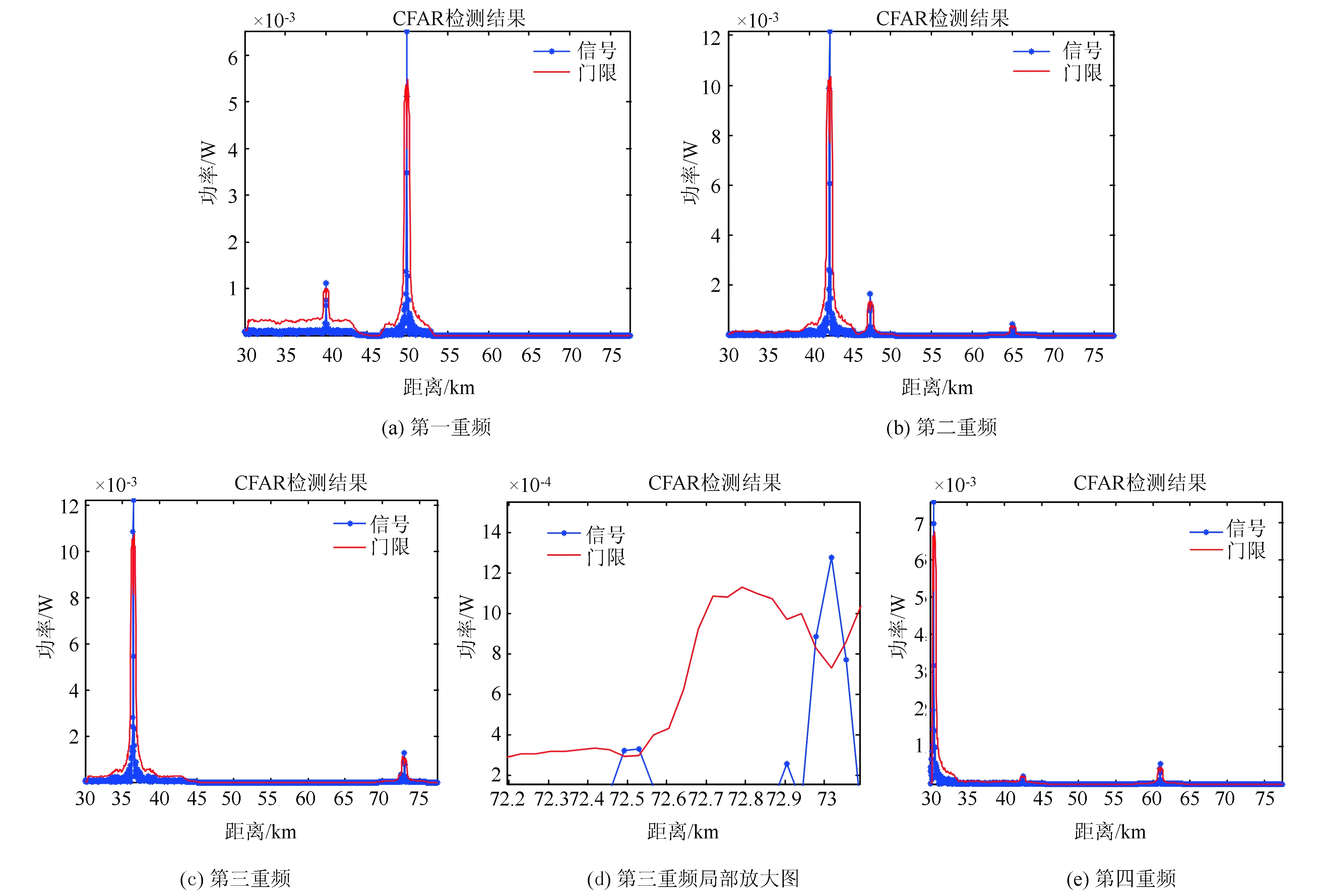
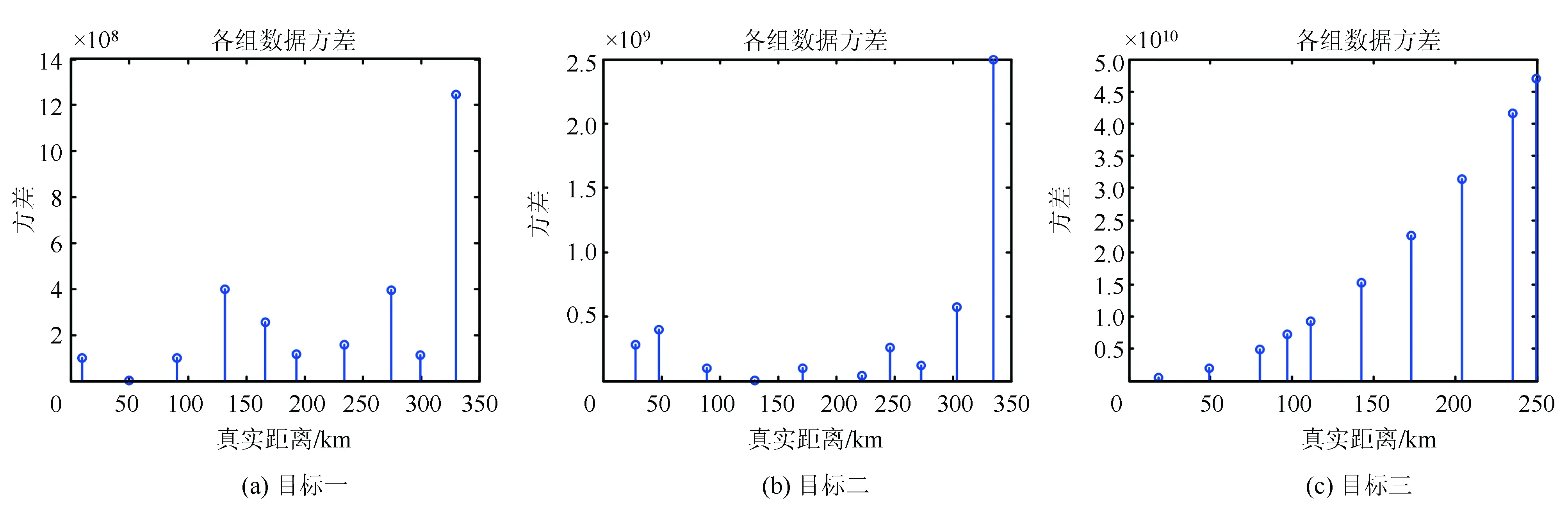
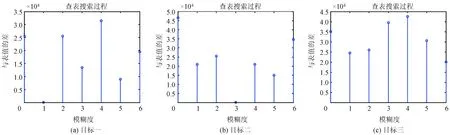
得到‖e1‖,‖e2‖…‖em‖m个值,在这些值中搜索选取最小值‖el‖,且满足‖el‖ 当测量不存在误差时,解出的目标距离会与实际的目标距离重合,但当存在测量上的误差时,要取两者差值最小的距离点,也就是要取集合中求余后结果与视在距离最接近的那个数。为了消除测距误差对结果的影响,设置了最大误差门限C,只有小于它的最小值才被认为是正确的,提高了筛选法的可靠性。多目标情况下,若目标在某个重频上视在距离重合,视在距离向量r在该重频上会减少一个元素,导致无法同时解算出两个目标。 当回波中含有多个目标信息时,第k重复频率视在距离对应的可能值由向量变为了矩阵,将所有重频对应的可能值求出,在无测量误差的情况下,每个矩阵中均含有所有目标的真实距离。将第k重复频率作为基准重频,对于基准重频中的每一个模糊距离值,在其它各个重频的模糊距离中寻找与其最接近的值,直到筛选出真实目标。基准重频的选取必须遵循所有目标在该重频的视在距离不重合的原则。 筛选法是中国余数定理衍生的方法,最少要求N+1种相异的脉冲重复频率才能解开N(N>2)个目标对应的模糊问题[17],也就是说使用N重频的系统对目标进行解算时可以准确地对N-1个目标解模糊。 利用n重频对x个目标进行解模糊,各重频对应的最大不模糊距离为Ru1,Ru2,Ru3,…Run,在各重频上的所有目标的视在距离值为Rtk,t=1,2,3,…x表示目标数,k=1,2,3,…n表示重频数,雷达的最大探测距离为Rmax。 (1)根据各个重频测得的视在距离,求出各个重频上视在距离对应的所有可能距离值矩阵为 (10) 其中,i表示四个重频中最大的模糊度,计算公式为i=int(Rmax/Rumin)。由于目标和距离门会出现失配问题,因此四个求得的矩阵相同的行不一定是同一个目标的视在距离对应的可能值。 (2)寻找一个所有目标视在距离均不重合的重频作为基准重频,这里选第一重频举例。按顺序取出矩阵里的元素,与其他重频的矩阵Sk中的每个元素相减,并取绝对值,得到一个新矩阵为 (11) 式中,sij表示矩阵S1元素,k=2,3,4,…n,矩阵S1根据式(10)计算可得。 (3)对矩阵E2,E3,E4所有元素的最小值求平均值dij,将S1所有的元素都比较完后可以得到dij组成的一个矩阵D。 (4)对矩阵D每行的最小值,若dxm为矩阵D第x行的最小值,且小于最大误差门限C,则m为第x个目标的模糊度,则第x个目标的真实距离为real_Rx=(R11+ΔR)+m*Ru1。 当测量不存在误差时,解出的目标真实距离与目标实际距离是重合的,但是由于环境中杂波和目标自身速度的影响,测量不可能没有误差,因此就要在其余重频上找与该可能值最接近的点(步骤2,3,4)。Ek中的元素值的大小反映了第k个重频上所有可能值与基准重频中某个元素sij的接近程度,值越小,接近程度越高。矩阵D的元素表示了剩余所有重频与sij的接近程度,越接近说明四个重频中都包含这个可能值,则这个可能值是目标真实距离的可能性越大。在实际应用中,雷达一般采用四重频解模糊,重频数值相差不大,因此,本文没有考虑不存在所有目标视在距离均不重合的重频这种情况。 对解模糊能力而言,当目标的视在距离在某个重频重合时,传统算法会出现漏解的现象。使用该算法则可以在目标信息不完备的情况下正确解算,提高了解模糊的能力,对于重频的选取也没有太多的要求。并且当系统存在测距误差时,该算法也能正确地解模糊,体现了很强的解模糊能力。 以4重频解3个目标距离模糊为例。设雷达发射的四个重频分别为PRF1=5000 Hz,PRF2=4000 Hz,PRF3=3448 Hz,PRF3=3030 Hz,最小探测距离Rmin=30 km,最大探测距离Rmax=280 km,雷达距离分辨单元为150 m,目标的真实距离为50 km,130 km,260 km,各重频所对应的最大不模糊距离为Ru1=30 km,Ru2=37.43 km,Ru3=49.95 km,Ru4=74.66 km。测量误差门为±150 m。 根据实际中雷达信号处理的流程,解模糊是在恒虚警检测后进行,因此认为检测时目标的位置即是视在距离,检测结果如图2所示。 图2 各重频CFAR检测结果 根据给出的参数进行理论计算可以得出表1,由(a)可知,第一重频仅有两个目标视在距离,分别为49.99 km,40.01 km,可以看出有两个目标视在距离是重合的,由(b)(e)可知,第二重频和第四重频三个目标视在距离均没有重合,可以作为基准重频,本文使用了第二重频作为基准重频。由(c)和(d)可知,第三重频三个目标视在距离没有重合,(c)看起来只有两个目标的视在距离是因为某个目标的回波信号太弱,局部放大后就可以找到这个目标。图2中所有视在距离减去雷达最小探测距离后与理论值基本一致,测量值出现了一些误差,这是由于环境中有杂波和目标有一定的速度导致的。 表1 理论视在距离(km) 图3 一维集算法结果 3.2.1 一维集算法 由于传统一维集算法计算量太大,本文仿真采用文献[13]提出的一种一维集的改进算法,以第二重频为基准,得到仿真结果如图3所示。 根据图3可知,在目标一和目标二的真实距离上方差最小,这是由于这两个目标信息完备,一维集改进算法可以准确地进行解算。但是由于第一重频上目标一和目标三的视在距离是相同的,目标三的信息在第一重频缺失了,因此一维集改进算法无法在寻找与第二重频第三个目标所有可能距离最近的距离,造成了解算错误,无法找到第三个目标的真实距离值。 3.2.2 余差查表法 以第二重频为基准重频,得到筛选法解模糊结果如图4所示。 图4 余差查表法结果 由图4可知,由实际测得的三个目标的视在距离经过运算查出余差表对应的模糊度为1,3,6。由式(4)可知,目标的真实距离分别为49.99 km,130.01 km,259.95 km,基本与目标真实距离一致。然而目标三的模糊度对应的差值远远超过了理论所 设置的±3个距离单元的误差门限,不能算作余差查表法的解,因此不能说目标三被正确解出。 3.2.3 筛选法 以第二重频为基准重频,得到筛选法解模糊结果如图5所示。 图5 筛选法结果 由图5可以看出目标一和目标二可以准确地由筛选法解算出来,而且误差很小。由于目标一和目标三在第一重频上视在距离是重合的,(c)中虽然在目标真实距离处误差最小,但还是远远超过了规定的最大误差门限±3个距离单元,会被判定为不正确的结果,因此只能算解出了两个目标。 3.2.4 改进算法 以第二重频为基准重频,得到改进算法解模糊结果如图6所示。 由图4结果可以看出,目标在50 km,130 km和260 km时,差值最小,与仿真参数一致,说明该方法可以很好的解多目标距离模糊,并且可以很好地解决两个目标视在距离重合的问题。在测量误差为±1距离单元的情况下也可以正确解模糊,说明该算法有一定的容错性,比较可靠。 图6 改进方法结果 本仿真实验在处理器为AMD A8-4555M APU(1.6 GHz),安装内存为4G的硬件环境和MTALAB 2014a的仿真环境中进行。通过仿真计时,改进的一维集算法的计算时间为1.224430秒,余差查表法的为1.183520秒,筛选法的为0.0022512秒,改进算法的为0.011971秒。筛选法计算时间为改进算法的18.8%,说明改进算法以增大计算量的代价解决了多目标情况下目标距离重合时筛选法无法正确解算目标真实距离的问题。但是从其他两种算法的计算时间上看,改进算法的计算速度还是优于这两种算法的。仿真结果说明了改进算法不仅拥有很强的解模糊能力,并且用拥有良好的实时性。 筛选法具有很好的实时性和很强的解模糊能力,但当目标视在距离重合的时候不能准确地进行解算。本文提出的方法不仅可以有效地进行目标匹配,并且很好的解决了目标视在距离重合时不能准确解算的问题。该算法计算原理简单,计算方法简便快捷,实用性较强。通过仿真分析,仿真结果验证了本文方法的正确性和有效性。2 筛选法改进算法
2.1 算法思想
2.2 算法实现步骤
2.3 算法性能分析
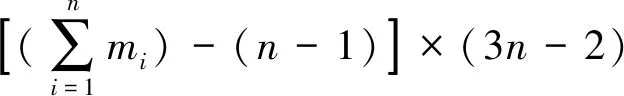
3 仿真实验
3.1 目标的视在距离

3.2 算法比较分析


4 结 语

