基于指数试探的稀疏度自适应匹配追踪算法*

于金冬，芮国胜，田文飚，董道广，于志军

（1.解放军91206部队，山东 青岛 266108；2.海军航空大学信息与信号处理山东省重点实验室，山东 烟台 264001）

0 引言

压缩感知（Compressed Sensing，CS）是一种新的信号压缩和处理理论，它突破了奈奎斯特采样定理的限制，同时完成了信号的采样和压缩，极大降低了信息存储、处理和传输的成本[1-2]。因此，该理论一经提出，便被广泛应用于遥感图像处理、医学图像采样等各个领域。

CS理论有3个核心问题：稀疏表示、压缩测量和优化重构。其中，优化重构直接影响着CS理论的应用效果，是最为关键的部分。贪婪迭代算法由于重建速度快且方法简便，应用十分广泛。它的基本思想是通过迭代，基于某种贪婪准则一次找出一个或多个待重构信号的构成元素，扩充支撑域以逼近信号的真实支撑。常用的贪婪算法有：匹配追踪（Matching Pursuit，MP）[3]、正交匹配追踪（Orthogonal Matching Pursuit，OMP）[4]、正则化正交匹配追踪（Regularized Orthogonal Matching Pursuit，ROMP）[5]、分段正交匹配追踪（Stagewise Orthogonal Matching Pursuit，StOMP）[6]、子空间追踪（Subspace Pursuit，SP）[7]等。这几种算法的抗噪声能力有限，为解决这一问题，Deanna Needell和Joel A TROPP提出了压缩采样匹配追踪（Compressive Sampling Matching Pursuit，CoSaMP）[8]，该算法引入了筛选回退的思想，提高了重构速度和鲁棒性。但是，上述算法都需要以稀疏度为先验信息，而实际问题中，信号的稀疏度往往是未知的，因此，出现了稀疏度自适应匹配追踪（Sparsity Adaptive Matching Pursuit，SAMP）[9]，它以固定步长逐步扩充支撑集，自适应地完成信号重建，但是步长的选择无法兼顾重构的精度和速度。近几年，学者们对稀疏度自适应重构算法进行了一些研究。杨成等[10]基于匹配测试获取稀疏度估计值，再通过子空间追踪重构信号，提出了SASP算法。Huang H等[11]引入弱匹配方法分别扩充和剔除原子，自适应获取稀疏度，提出了BAOMP算法。田文飚等[12]提出的BSAMP算法，基于分治思想预估稀疏度，然后通过自适应分组快速筛选出有效支撑集，进行信号重构。吕伟杰等[13]采用分段思想，先对半减小预估稀疏度，再逐一增加逼近，最后利用子空间追踪重构，提出了MASP算法。

1 CS理论框架

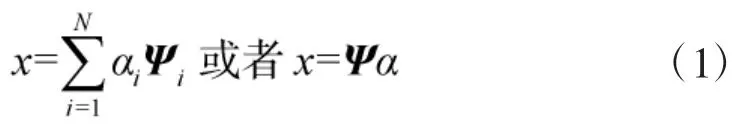
其中，Φ是M×N维观测矩阵，y是M×1维观测信号。将式（1）带入式（2）得：

信号的重构是利用M维观测信号y无失真恢复出N维原始信号x的过程。由于x是K稀疏的，因此，可转化成最小l0范数问题来求解，即：

由于观测维数M远小于信号维数N，因此，式（4）所描述的最小l0范数优化问题是一个NP-hard难题，数值计算复杂度高，而且极不稳定。文献[14]指出可以将该问题转化为求解一个更简单的l1范数优化问题来解决，即：

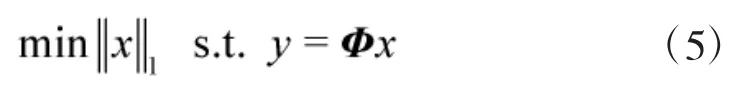
若要完成精确重构，观测矩阵Φ必须满足有限等距约束特性[15]（Restricted Isometry Principle，RIP）：

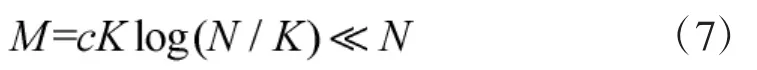
2 EtSAMP算法

2.1 指数试探思路

首先给出稀疏度欠量估计和过量估计的判据，如定理1和定理2所示。

证明：由文献[10]中给出的相关结论可知，若估计稀疏度 k≥K，则，其中，ΦT表示以T为索引的Φ中各列构成的子矩阵，为 ΦT的共轭转置。由于 K＜2K，根据δK的单调性可得，RIP常数δK≤δ2K，因此，，证毕。

由于引理1是充分不必要的，因此，在实际问题中，通常利用其逆否命题来判定估计稀疏度是否小于真实值，如定理1所示。

文献[12]给出了稀疏度过量估计的判据及证明，如定理2所示。

本文引入递减型指数函数进行试探，令预估稀疏度随着试探次数自适应发生变化，从而精确快速地逼近真实稀疏度。指数函数的基本形式如式（8）所示：

试探过程示意图如图1所示。

初始试探阶段：首先进行第一次试探，得到相应支撑集，若满足，说明稀疏度过量估计，即k＞K，转入下一次试探，使预估稀疏度不断减小，直至满足，说明稀疏度欠量估计，即k＜K，转入回溯试探阶段。

图1 指数试探过程示意图

回溯试探阶段：当k＜K时，令k=k+1，逐一增加预估稀疏度，直至再次满足，如此，便可得到有效估计的真实稀疏度。

该方法将试探过程分为两个阶段：初始试探阶段和回溯试探阶段。在初始试探阶段利用递减指数函数骤降的特性，进行粗略搜索，快速靠拢真实稀疏度；在回溯试探阶段以小步长逐步试探逼近，进行精细搜索，最终获得准确的稀疏度估计值。通过指数试探，不仅避免了SAMP等算法对步长选择的依赖，而且提升了试探精度，节省了运算时间。

2.2 算法步骤

算法的流程图如图2所示。

图2 算法流程图

详细步骤如下。

输入：观测矩阵Φ，观测向量y。

Step 1 指数试探稀疏度

4）i=i+1，逐一增加稀疏度估计值的大小，即ki=ki+1，直至满足，令k=ki，完成对稀疏度的准确估计。

Step 2 筛选回退重构

Step 3 弱匹配剪枝

Step 4 迭代停止条件

2.3 算法可行性说明

Step1 将稀疏度试探分为两个阶段，先粗略搜索后精细搜索，在2个判据的共同约束下，逐步逼近真实稀疏度，为后面的重构提供了可靠的先验信息，既保证了试探速度，又兼顾了试探精度，避免了SAMP算法对步长信息的依赖以及RAMP算法[16]中阈值对重构精度的影响。

Step2 首先根据相关性批量选择2k个原子构成预选集，然后回退筛选出候选集，重构得到估计信号，本质上是一种回溯类方法，同时提高了重构速度和抗噪声性能。

Step3 采用弱匹配原则选取重构向量大于一定阈值的原子，并将其索引加入支撑集，剪枝得到信号的逼近值。已有实验表明[11]，弱匹配参数ξ在[0.4，0.8]之间取值时，可以兼顾算法性能和运算速度。

Step4 通过对比前后两次残差值的大小，判断是否停止迭代。这是因为每进行一次迭代，算法都将选择相关性最大的一批原子构成支撑集，因此，残差值是不断减小的，而一旦满足，说明此时支撑集中已经引入了错误的原子，因此，应当退出迭代，保留上一次的迭代结果，输出重构信号。

3 实验结果及分析

通过分析可以看出，EtSAMP算法能够通过调整参数来实现任意稀疏比条件下信号的准确试探及自适应重构，由于工程应用背景各不相同，这里不一一穷举。文献[17]中指出，用压缩感知理论处理稀疏比较低的遥感图像，更有利于保护图像边缘，保留图像细节，抑制噪声干扰。

选取随机生成的一维稀疏信号作为测试信号（N=512），生成M×N维高斯随机矩阵作为观测矩阵，观测数（c取 2，4），弱匹配参数ξ取0.4。为降低随机因素的影响，所有数据都是经过1 000次蒙特卡洛仿真后求得的平均值。

3.1 相关参数的确定

由稀疏度欠量和过量估计判据可知，RIP常数δ2K关乎判别尺度的大小，进而影响试探的精度；由指数函数的性质可知，参数b能够改变其变化趋势，从而影响试探的速度。因此，确定二者的最优取值十分重要。

首先讨论δ2K对试探结果的影响，固定参数b，令真实稀疏度K=50，进行 20次实验，比较δ2K取不同值时稀疏度的试探结果，如图3所示，可以看出，当δ2K=0.2时，试探结果约为53，与真实稀疏度最为接近，因此，为保证试探的准确性，这里取 δ2K=0.2。

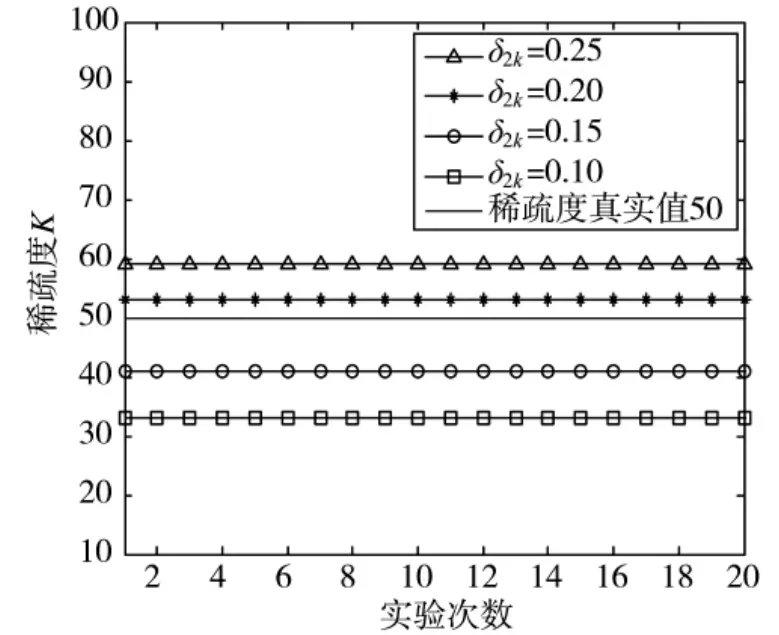
图3 δ2K与稀疏度试探结果

下面固定δ2K=0.2，研究参数b与试探次数的关系，结果如图4所示。

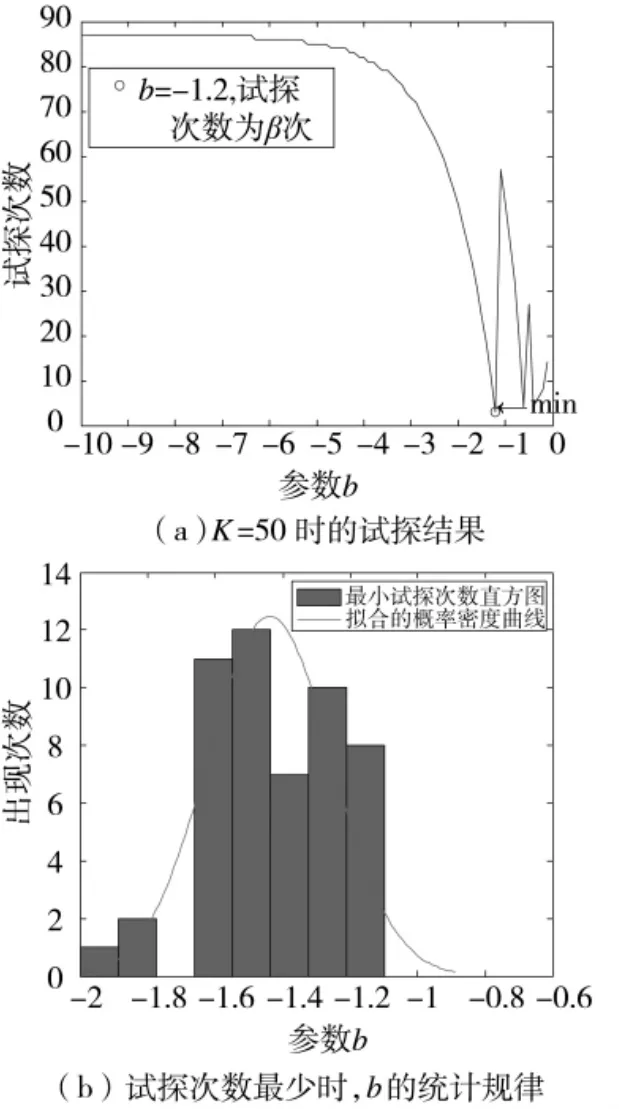
图4 b与试探次数的关系

图4（a）中，令真实稀疏度K=50，观察试探次数最小时b的取值。结果表明，当b=-1.2时，试探次数最少，只需3次。此外，试探次数随着b的增加呈现非线性变化，二者没有明显的线性关系，这是由指数试探先粗略搜索后精细搜索的性质决定的。图4（b）是图4（a）方法的推广，令稀疏度由1变化至128（稀疏比为0.25），统计当试探次数最小时，b取值的出现次数直方图和拟合概率曲线。结果表明，当b在[-2.0，-1.1]之间取值时，试探次数易达到最小，特别是当b=-1.5时，出现的概率密度最高。因此，为保证试探的效率，这里取b=-1.5。

3.2 稀疏度试探结果

为了进一步验证指数试探方法的可行性，令稀疏比K/N从0.1至0.25变化，比较估计稀疏度k和真实稀疏度K的值，结果如图5所示。

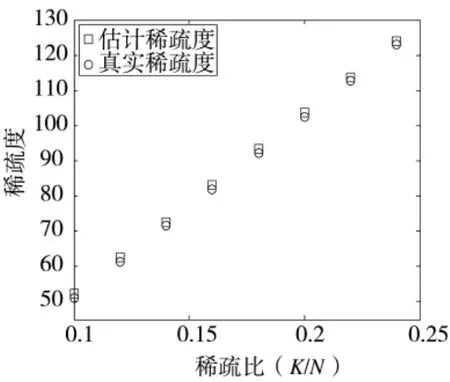
图5 估计稀疏度与真实稀疏度对比

可以看出，估计稀疏度与真实稀疏度基本重合，说明通过指数试探得到的结果与真实稀疏度十分逼近，该方法是可行的。此外，实验结果表明，估计稀疏度略微高于真实稀疏度，保证了即使稀疏度估计出现偏差，也能够包含重构所需的全部信息，进而重构出原始信号，提高了重构过程的稳定性。

3.3 重构性能比较

首先比较几种稀疏度自适应重构算法的运行时间。令稀疏比K/N从0.05至0.25变化，SASP算法中，α=0.7，δK=0.3，SAMP算法中步长取2，opt=0.001[10]。图6展示了在不同稀疏比条件下，4种算法的重构时间。

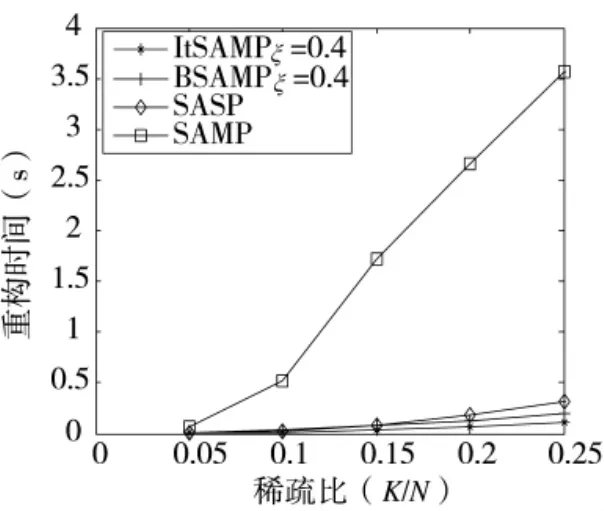
图6 不同算法重构时间比较

由图6可以看出，在稀疏比小于0.25时，各类算法的重构时间均随稀疏比的增大而增加，EtSAMP算法的重构时间最短，低于相同弱匹配条件下的BSAMP和SASP算法，远小于SAMP算法，优势十分明显。这是由于SAMP算法依据步长逐步扩充支撑集，在选择原子的候选集和最终支撑集时需要较大的计算量，SASP和BSAMP算法在试探稀疏度时步骤较多，EtSAMP算法利用指数函数提高搜索速度，试探次数最少，而且在重构过程中批量选择2k数目的原子与重构信号原子的支撑集做并集，节省了时间。

下面将EtSAMP算法与几种经典的贪婪算法进行对比，其中CoSaMP、OMP、ROMP算法中代入指数试探出的稀疏度k。实验结果如图7和图8所示。通常认为，如果重构信噪比SNR大于40 dB，则重构成功，即式（9）：

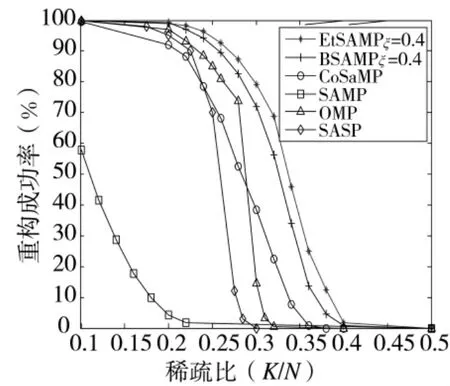
图7 重构成功率随稀疏比变化曲线

由图7可得，当稀疏比小于0.25时，EtSAMP算法的重构成功率基本稳定，不低于97%，而其他5种算法的重构成功率均有不同程度下降，当稀疏比提高到[0.25，0.4]之间时，EtSAMP算法的优势更加突出，重构成功率远高于其他算法，当稀疏比大于0.4时，6种算法都无法成功重构信号。

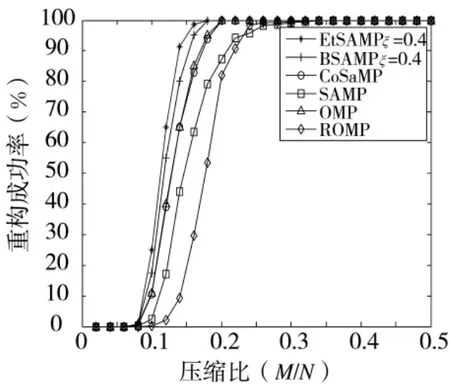
图8 重构成功率随压缩比变化曲线

从图8可以看出，当压缩比小于0.075时，几乎所有算法都无法实现重构，随着压缩比逐步增大，重构成功率快速提升，特别是当压缩比到达0.15时，EtSAMP和BSAMP算法就已经能够高概率完成重构，远远优于其他算法。

图9直观给出了当稀疏度取不同值时，残差随迭代次数的变化情况。

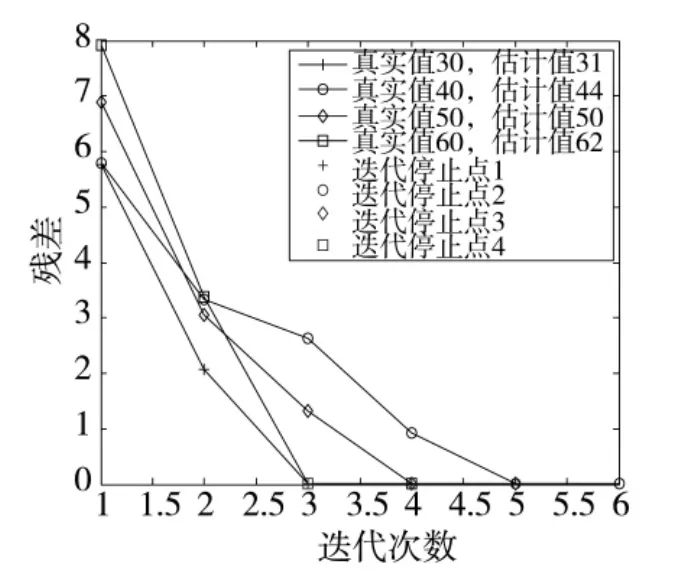
图9 残差随迭代次数的变化情况

由图9可见，当迭代停止条件尚未满足时，残差会随着迭代次数的增加而减小，直至，即最新一次迭代的残差大于上一次迭代的残差，此时无论稀疏度取何值，信号的重构信噪比均大于40 dB，认定重构成功。因此，以作为停止迭代条件是合理的，且说明EtSAMP算法具备一定的收敛性。

4 结论

利用指数函数特性，同时结合筛选回退思想和弱匹配原则，提出了一种新的稀疏度自适应重构算法。算法利用指数函数特性将稀疏度试探过程分为两个阶段，在初始试探阶段粗略搜索，在回溯试探阶段精细搜索，快速准确地逼近真实值，然后通过筛选回退扩充信号的支撑集，再采取弱匹配剪枝的方法精确重构出原始信号。算法较好解决了贪婪算法需要预知信号稀疏度，以及现有稀疏度试探方法效率较低的问题。实验表明，新算法的试探结果更加准确稳定，重构成功率提升，特别是当稀疏比小于0.25时，重构时间少于其他算法，适合处理低稀疏比的遥感图像问题。