新型四极轨道电磁发射器

刘 明，舒 涛，薛新鹏

（空军工程大学防空反导学院，西安 710051）

0 引言

电磁轨道发射器是电磁发射器的一种，它在新概念武器中具有广阔的应用前景[1-4]。脉冲电源、轨道、电枢和控制电路是它的重要组成部分。电流从一根导轨经电枢流向另一导轨，流经两导轨的电流在导轨之间形成强磁场，强磁场与流经电枢的电流相互作用产生强大的电磁力，推动电枢沿导轨加速并最终离开导轨，这就是传统电磁发射器的工作原理。电枢及轨道设计对其性能有着重要影响[5]，固体电枢具有欧姆损耗较小、能量转换效率高的特点，是目前研究的热点[6-9]。固体电枢的结构设计会影响通过电枢内部的电流分布、焦耳热分布以及电枢所受电磁驱动力[10-11]。轨道的布局构造能影响轨道间磁场的分布，从而影响电磁驱动力的大小。电磁轨道发射作为现代军事武器的发展方向，仅有大动能是远远不够的，现代化战争讲究的是精确高效，所以必须提高电磁轨道发射器的发射精度和命中率，才能适应现代化战争。选择合理的电枢模型及适合的导轨，不仅可以提高电枢所受的电磁驱动力而且可以提高发射精度，实现现代化战争的需要。

本文首先给出了新型四极电磁发射器模型，介绍电磁轨道发射电磁场基本理论，并对该模型进行理论分析；其次利用ANSYS Maxwell 3D对模型进行有限元仿真，获得推进力、磁场及电流分布等主要信息，与传统轨道炮进行对比，得出电磁力大小与轨道电流的关系。

1 发射模型

新型四极轨道电磁发射器模型如图1所示。抛体运动方向为Y轴。该发射器主要由四极轨道和抛体组成，抛体外侧为长方体轨道，抛体内侧为圆柱体轨道，轨道的材料是相同的，抛体为三叶花瓣状。

图1 四极轨道电磁发射器模型

1.1 发射过程

在最初的发射阶段，抛体在四极轨道中静止等待脉冲电流的进入。在发射过程中，脉冲电压源对圆柱体轨道进行放电，通过三叶花瓣状抛体连接，流入120°等间距分布的长方体轨道形成回路。同时，三叶花瓣状抛体获得3组径向电流，四极轨道产生的环向磁场环绕在抛体周围。环向磁场与径向电流相互作用，产生轴向力推动抛体高速发射。

1.2 四极轨道设计

四极轨道电磁发射器一项关键技术是四极轨道的结构设计。四极轨道布局和3组电流的流动方向具体如图2所示，图2为四极轨道电磁发射器的俯视图，抛体外侧三极长方体轨道120°均匀间隔分布，电流从圆柱体轨道流入，通过抛体后分别流入三极长方体轨道，最后流出形成回路。围绕在长方体轨道周围的圆圈是电流产生的磁感应线圈。因为电流大小是相等且均匀分布的，所以电流与磁场相互作用产生的安培力能平稳推动抛体向外发射而不会发生偏斜。同时这样的轨道设计可以提高发射过程中的稳定性，相比于传统的轨道电磁发射器只有两根导轨保证其稳定性，这样的轨道设计不光增加了抛体外侧的轨道数量，而且通过中间的圆柱体轨道使稳定性效果更优。这样的抛体设计能有效地减缓其振动，增加射击的准确度。

图2 抛体及电流流向

1.3 抛体设计

由以上轨道的设计方案可知，抛体是中空的，允许圆柱体轨道贯穿抛体，抛体外边缘需与外侧三极长方体轨道实现全接触。为了更清楚地了解三极长方体轨道间抛体电流的分布，首先将抛体设计成近似圆形，这样就可以获得抛体中电流分布，得到仿真结果如图3所示。

图3 抛体电流分布矢量图

抛体中的电流以最短路径从高电势流向低电势，图3中箭头主要集中在长方体轨道和圆柱体轨道的连线上，在抛体的其他位置箭头分布很少，说明电流主要流经轨道连线上，其他位置电流较少，且电流的分布是中心对称的，故最终将抛体设计成图4所示模型。三叶花瓣状抛体的设计，在满足电流畅通的同时降低发射系统重量。

图4 三叶花瓣状抛体

2 理论分析

2.1 空间磁感应强度分析

由毕奥-萨伐定律[12]知，对于长为l，电流为I的通电直导线来说，其周围任意一点P的磁感应强度为

其中，真空磁导率μ0为常数；ρ为P点到电流元的垂直距离；θ1和θ2分别为P点与通电直导线电流流向的夹角，若导线可视为无限长，则。这时上式变为

同时由于轨道电磁发射器在发射过程中存在电流趋肤效应，电流主要分布在导轨表面。为了简化计算，假设电流全部分布在导轨的表面上，长方体轨道就可以忽略其厚度当作金属薄板。假设轨道宽为b，通有电流I。为了方便求解轨道外一点P的磁感应强度，把薄板分成许多宽为dx的长细条，每根细条可看成通有电流dI的长导线，其中

它在P点产生的磁感应强度的大小为

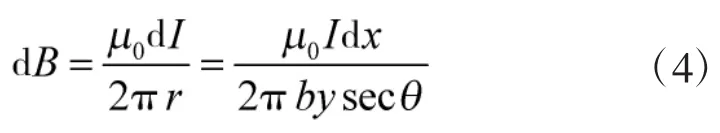
其方向与位矢r垂直，如图所示，不同位置的细条在P点处产生的dB各不相同。因此，将dB分解为沿X轴和Y轴的两个分量dBx和dBy，但由于对称性可知，与原点对称位置处的任意两细条产生在P点的dB沿Y轴方向相互抵消。因此，

又由

代入上式得

因为

所以

由于电枢是三叶花瓣状，故主要考虑长方体轨道和圆柱体轨道之间空间的磁感应强度，可近似地认为空间一点P的磁感应强度只受临近长方体轨道和圆柱体轨道中电流的影响，而不受距离较远的两极长方体轨道电流的影响。圆柱体轨道电流是长方体轨道电流的3倍，同理，圆柱体轨道在空间一点P产生的磁感应强度为

式中，y*表示空间点P到圆柱体轨道表面的距离。

由于电枢和轨道的尺寸已经确定，所以长方体轨道表面到圆柱体轨道表面的距离也是一个常数，设它为d，则

由以上分析可知，空间任一点P的磁感应强度为

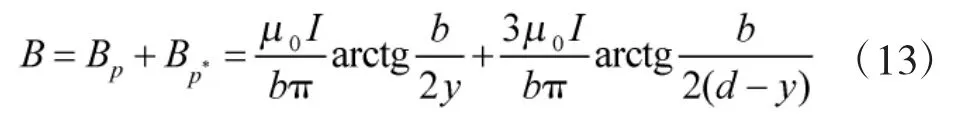
2.2 电磁力分析

当电流流过磁场中的电枢时，电流和磁场正交产生安培力推动电枢向外发射。由于已经明确空间中磁感应强度的分布，它随着空间点P位置的改变而改变，取一小段距离dl，在一小段距离之内认为磁场B不发生改变，为恒定值，通过对距离的积分求得电枢所受电磁力。根据电磁力定律，在磁场B的作用下，电流元所受到的电磁力为：

电枢上每段距离受到的安培力都是同向的，故不需要对力进行分解计算，电枢三叶花瓣其中一个受到的安培力

故电枢受到总的安培力为

3 有限元仿真

3.1 模型假设

在进行有限元仿真之前，为了简化计算，需要对模型做出一些合理的简化假设：

1）在发射过程中，因为轨道、电枢的形变量都很小，对电磁场基本无影响，所以进行电磁分析时可以忽略电枢、轨道的形变；

2）实际情况中电枢与轨道的接触不可能为全接触，为了简化计算，不考虑模型中的接触面与实际接触面的差异，假设电枢与轨道间是全接触；

3）相比轴向电磁力，径向的正压力较小，故可忽略电枢和轨道间的滑动摩擦力，同时为了简化计算忽略空气阻力。

3.2 有限元仿真分析

通过三维有限元软件模拟，对新型四极轨道电磁发射器进行仿真分析。抛体的磁感应强度分布如图5所示，以及随着电枢厚度变化磁感应强度的变化如图6所示。

图5 抛体磁感应强度分布

图6 磁感应强度变化情况

可以看出磁场主要分布在抛体的底部，依次往上磁场层层递减，顶部磁场强度最弱，抛体底部靠近圆柱体轨道周围磁场最强，这是因为电流主要由电枢底部传导给长方体轨道，且抛体底部圆柱体轨道周围的电流最集中。从图6可以得出随着电枢厚度增加磁感应强度下降速度增加，最后几乎降为零，曲线光滑程度不是很好，是因为节约运算空间使得电枢的网格划分比较粗糙所致。

四极环向磁场的矢量分布如图7所示，抛体靠近长方体轨道的地方磁场方向与径向垂直，这能保证最大的受力，抛体底部靠近圆柱体轨道处磁场最大。抛体底面电流分布如图8所示，抛体电流主要分布在靠近四极轨道处，三叶花瓣状电枢起到了引流的作用，电流沿径向流动。

图7 四极环向场矢量

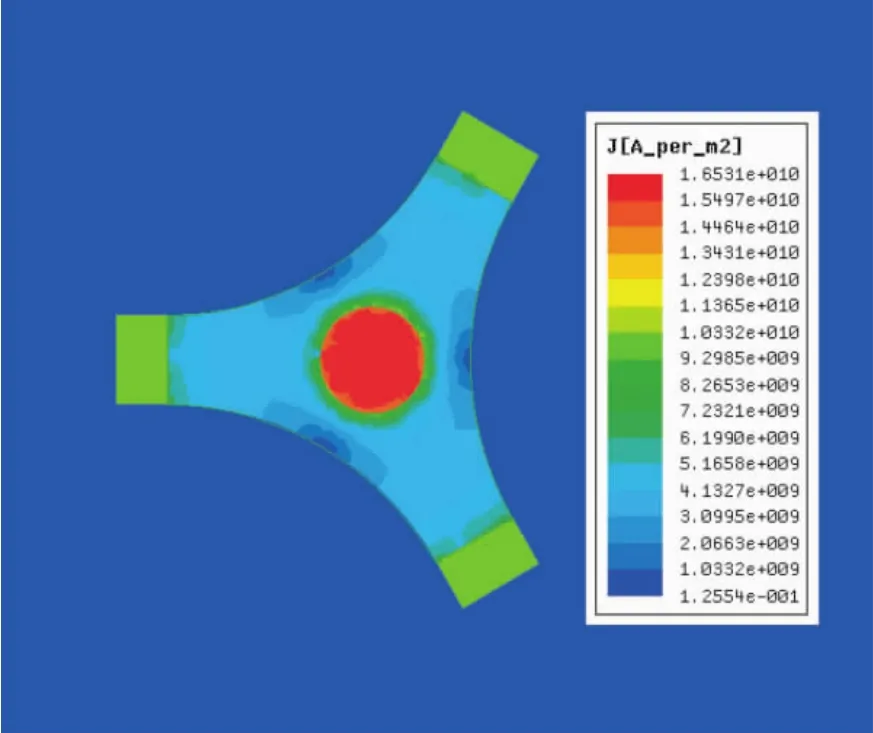
图8 电枢底部电流分布

3.3 推进力对比

为了验证新型四极轨道电磁发射器较传统轨道炮在推进力方面的优势，对下页图9所示传统电磁轨道炮进行有限元仿真分析，并将结果进行对比。

假设四极轨道电磁发射器和传统轨道炮电枢的厚度保持不变，轨道的材料和长度不变，加载电流大小与边界条件保持不变，输入电流均为300 kA，则作用在抛体的推进力对比如表1所示。

图9 传统电磁轨道炮模型

表1 推进力对比情况

通过前面的理论计算可知，X和Z方向的力相互抵消，只有在Y方向受到推进力。传统电磁轨道炮的轴向推进力是16 857 N，force_x和force_z干扰力很小。四极轨道发射器轴向推进力为37 317 N，与理论计算值39 562 N存在一定误差，这是由于三极长方体轨道中电流产生的磁场存在一定的相互抵消，但与传统轨道炮相比，force_y增加近两倍，其他两个方向的干扰力也很小，验证了四极轨道电磁发射器的合理性。

4 轨道电流对推进力的影响

根据第2节理论计算可以得出：随着轨道电流的增大，抛体所受推进力也会随之增大。为了进一步验证此理论，利用ANSYS Maxwell 3D来获得推进力随轨道电流的具体变化情况。

在模型仿真中，轨道材料选用黄铜，抛体选用铝，选用真空作为边界条件，轨道及抛体的结构尺寸保持不变，电流的变化范围从0 kA～500 kA。得到的结果如图10所示。

图10 推进力随电流变化情况

结果显示，随着轨道电流的增加，抛体受到的推进力也随之增加，起始阶段随着电流的增加，推进力增长幅度不大，但随着电流的等幅增长，推进力增长的趋势变大，增长的斜率变大。

5 结论

本文介绍了一种新型四极轨道电磁发射器。该发射器电流由中间圆柱体轨道流入，流经电枢后从外侧三极轨道流回电源形成回路，电枢在轨道间强磁场的作用下，产生巨大轴向推力使抛体发射出去。在与传统轨道的对比中发现，新型四极轨道电磁发射器能产生更大的轴向推力；在对电枢的磁场分析中发现，新型四极轨道发射器电枢的磁场集中于下部，上部磁场很小；随着轨道电流的增加，抛体所受推进力也会增加，符合理论计算结果；此外，新型四极轨道电磁发射器的结构设计对于抵抗发射过程中的剧烈振动，提高发射精度有重要的意义。总的来说，新型四极轨道电磁发射器有较大的优势，未来可用于导弹和卫星的发射等多方面。