基于TS-MMPF的机动弱目标TBD算法*
谭顺成,于洪波
(海军航空大学信息融合研究所,山东 烟台 264001)
0 引言
检测前跟踪(Track-Before-Detect,TBD)算法[1-12]是一种低信噪比情况下对目标进行检测和跟踪的有效方法。目前,典型的TBD算法主要包括Hough变换[2-3]、最大似然[4]和动态规划[5-6]以及粒子滤波(Particle Filter,PF)[7-12]等方法。其中,基于 PF 的TBD算法因对非线性非高斯系统具有较好的适应性,是目前研究的热点,基于多模粒子滤波(Multiple Model Particle Filter,MMPF)[7]的 TBD 的算法就是检测机动弱目标的典型代表。然而基于MMPF的方法,一方面只是在每个时刻给出了目标状态的估计值,不能给出目标的航迹信息;另一方面,当粒子出现严重退化时,粒子的多样性急剧减少,粒子集比较单一,容易造成存在却检测到目标不存在的问题,即目标漏检。
本文立足于解决此类问题,在基于MMPF的TBD方法基础上,提出一种基于航迹平滑(Track Smoothing,TS)的MMPF(TS-MMPF)机动弱目标TBD算法,该方法对MMPF的输出结果进行航迹起始、关联及滤波,当检测目标不存在时利用航迹预测值代替估计值,对目标航迹进行平滑形成暂定航迹,最后借助后续时刻的估计值判断是否维持或撤销暂定航迹,有效克服因粒子退化造成的目标漏检问题,提高了目标航迹的稳健性。
1 系统模型
1.1 状态模型
考虑单目标在x-y二维平面机动运动的场景,并假设在任意观测时间内目标的运动模式服从匀速直线运动、顺时针坐标转动以及逆时针坐标转动3种模式中的一种,以表示3种运动模式集合,其中,1代表匀速直线运动,2代表顺时针坐标转动,3代表逆时针坐标转动。以表示目标状态,其中,和Ik分别表示目标位置、速度和强度状态,目标状态转移方程为
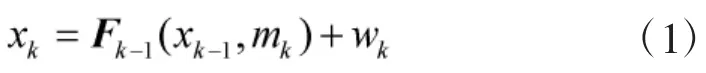

式(3)对应于坐标转动模式
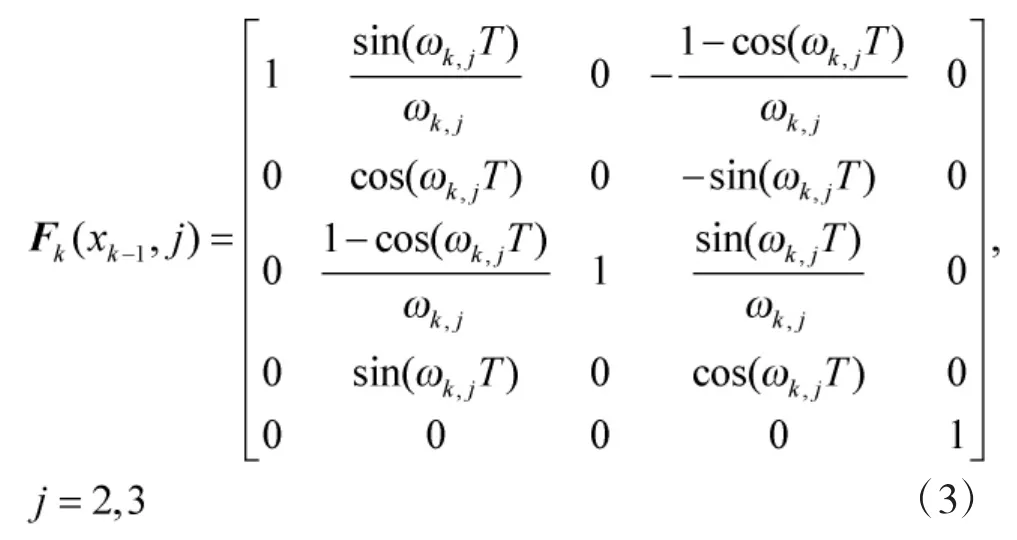
式中,T为传感器扫描周期,另外

分别对应于顺时针坐标转动和逆时针坐标转动,αm>0是一个典型的机动加速度。
假设mk作用于时间段,目标某一时刻只遵循一种运动模式,整个运动过程中,各种运动模式之间的转换可描述为3态的1阶Markov链。模式转移概率矩阵∏m,其各元素
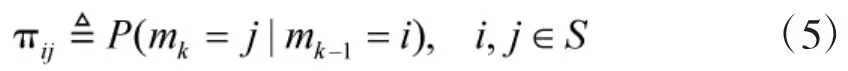
k时刻目标可能存在于传感器警戒区域内,也可能不存在,以变量Ek对此建模。描述为2态的1阶Markov链,即。0表示目标不存在,1表示目标存在。并定义目标“新生”概率Pb和“死亡”概率Pd为
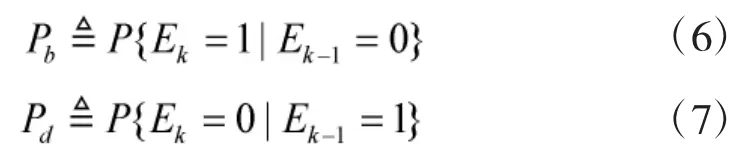
其转换概率矩阵为
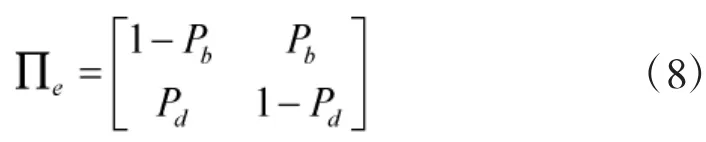
1.2 量测模型
假设传感器提供的监控区域内的二维图像,每张图像包含m×n个分辨单元。每个分辨单元对应于一个的区域,第(i,j)个单元的中心定义为。以表示时刻k
分辨单元(i,j)的观测数据
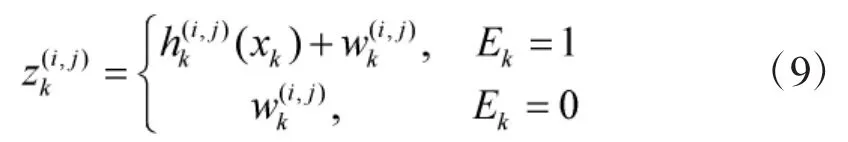
其中
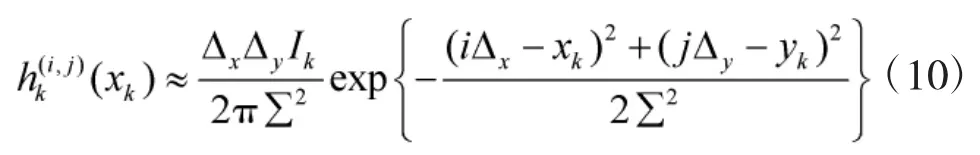

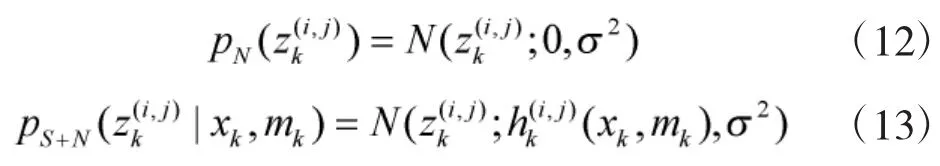
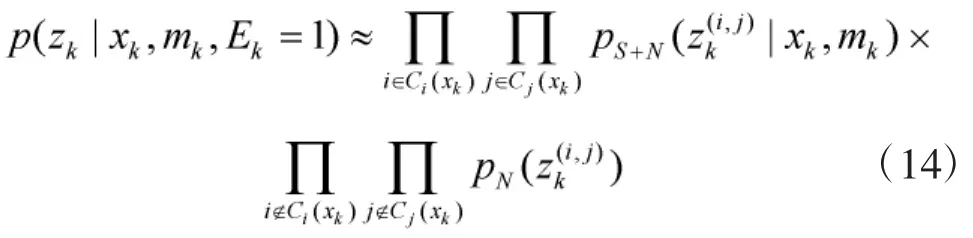
2 算法实现
2.1 滤波器初始化
5)根据目标初始运动模式概率φ0初始化目标运动模式变量;
2.2 粒子集预测
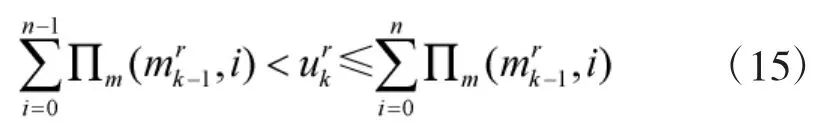
② 根据目标初始运动模式概率φ0生成预测的目标运动模式变量;
3)将对“持续存在”粒子进行预测得到的粒子集和“新生”粒子集进行合并,得到总的预测粒子集。
2.3 粒子权重更新和重采样
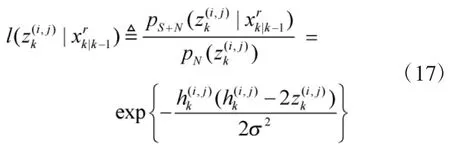
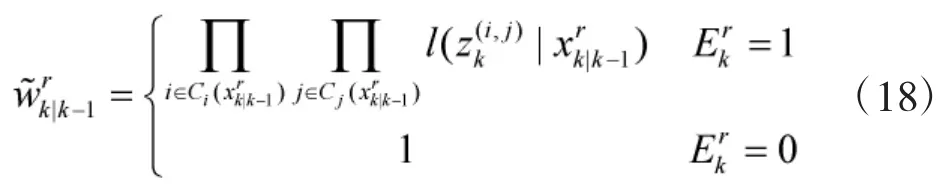
2)归一化粒子权重
2.4 目标状态估计和航迹平滑
计算目标存在概率
① 设置目标存在标志flag=2;
② 估计目标状态
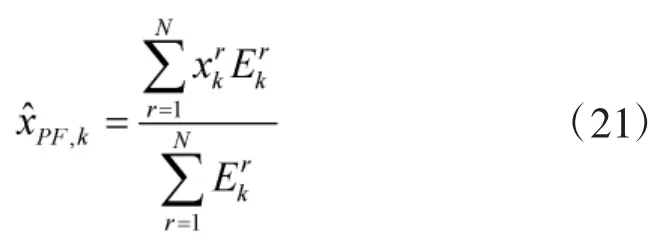
及状态协方差
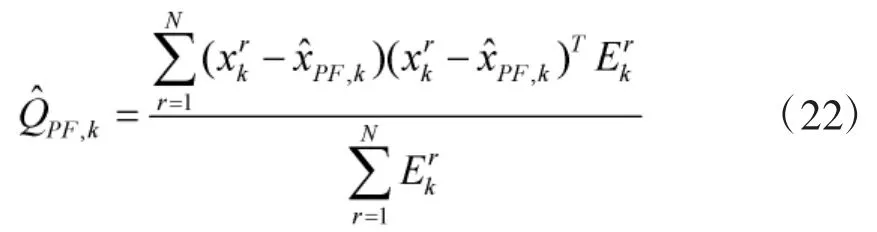
③ 估计目标按各模式运动的概率
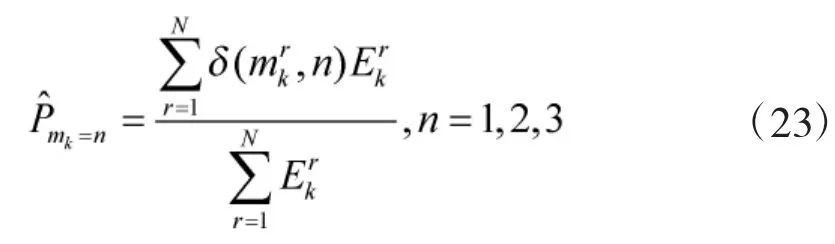
及当前时刻目标的运动模式
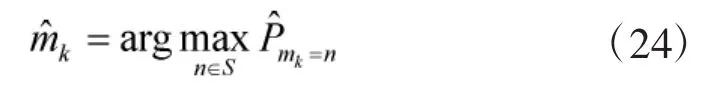
其中
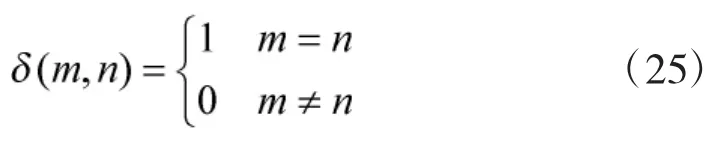
③若flag<0,当前时刻没有目标航迹,令flag=0。
基于TS-MMPF机动弱目标TBD算法的基本流程如下页图1所示。
3 实验仿真
设置一个与文献[8]相同的仿真场景,进行实验仿真,仿真总时间为45 s,其中目标从第7 s开始出现,首先沿x轴方向作10 s匀速直线运动,接着作5 s逆时针转弯运动,此后进入10 s的匀速直线运动,最后作5 s的顺时针机动转弯,直到37 s消失,一共存在30 s。假设过程噪声w为零均值高斯白噪声,其协方差矩阵为
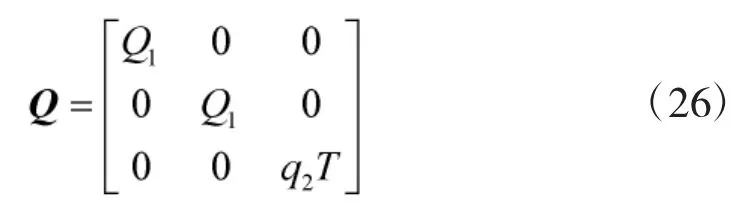
其中
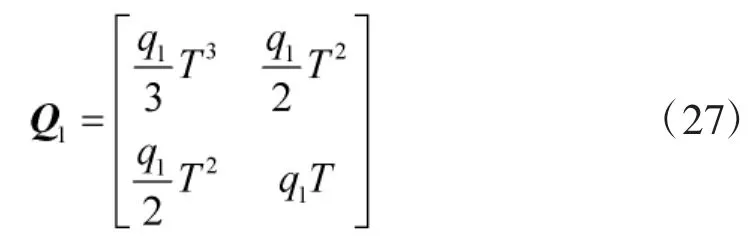
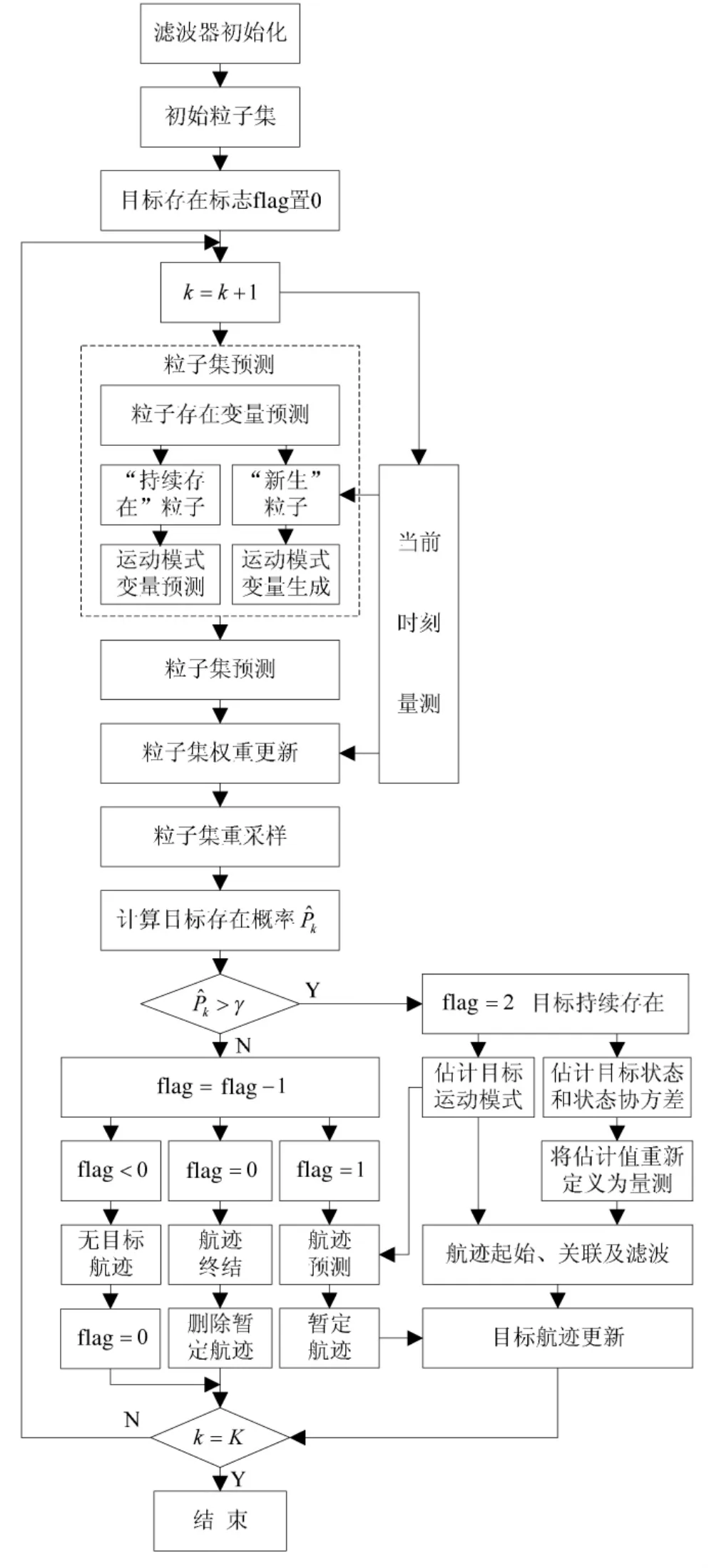
图1 算法流程图
q1和q2分别表示目标运动状态和目标强度的过程噪声。仿真中设置为q1=0.001,q2=0.01,机动加速度αm=1.08,传感器采样间隔T=1 s,每一秒产生一帧观测图像。观测区域m×n为60×60,每一个分辨单元的尺度设置为 Δx=Δy=1。目标初始位置为(20,20),速度为(2,0)分辨单元每秒。目标初始存在概率,“新生”粒子3种运动模式概率分别为 φ1=0.9,φ2=0.05,φ3=0.05,持续存在粒子的运动模式转移概率矩阵[8]为

图2为信噪比为6 dB时传感器得到的4帧(第1帧、7帧、20帧和38帧)量测数据的灰度图,由仿真场景设置可知,第1帧和38帧目标实际不存在,第7帧和第20帧目标实际存在,但是由于信噪比较低,目标回波信号湮没在噪声信号里,并不能从这些量测数据直接判断出目标是否存在,更不能直接获得目标的位置信息。

图2 SNR=6 dB时的4帧量测数据灰度图
图3~图6分别给出了目标信噪比为6 dB时基于MMPF和本文TS-MMPF的TBD算法的仿真结果,其中图3和图4分别为基于MMPF估计目标存在概率(底部的“*”号表示当前时刻目标实际存在于监控区域内)和估计的目标点迹与真实的目标航迹对比,图5和图6分别为TS-MMPF估计的目标存在概率和目标航迹与真实的目标航迹对比。
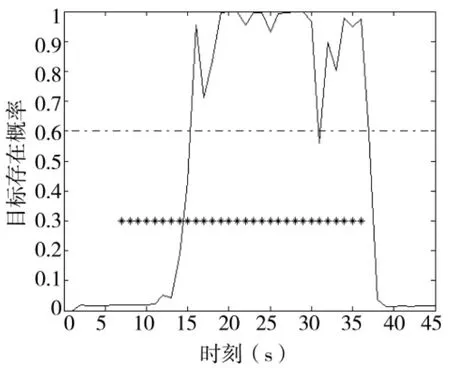
图3 MMPF估计的目标存在概率
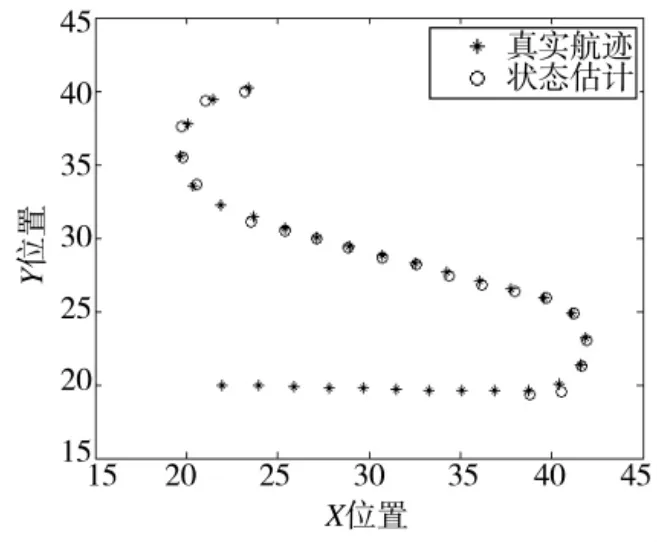
图4 MMPF估计的目标点迹和真实目标航迹对比
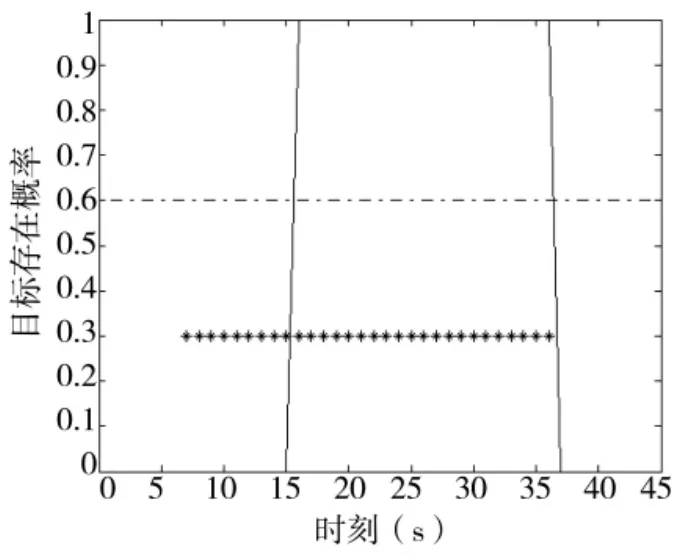
图5 TS-MMPF算法估计目标存在概率
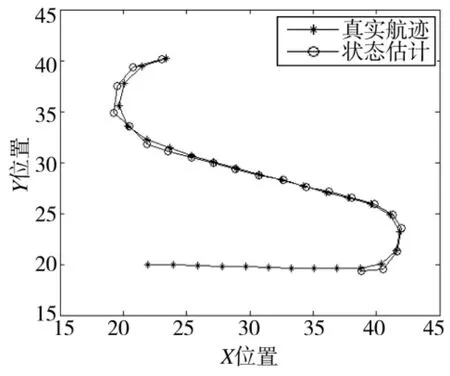
图6 TS-MMPF算法估计的目标航迹与真实航迹对比
由图4和图5比较可以看出,经过一段时间的积累后,MMPF仅给出了估计的目标点迹,不能给出目标的航迹信息,而本文的TS-MMPF算法可以直接给出目标航迹。图3 MMPF估计的目标存在概率存在一定的起伏,如果设置判断目标是否存在的检测门限为0.6,从图3可以看出,MMPF算法在第7 s~第16 s以及第31 s出现了目标漏检(同时体现图4的相应时刻不能给出目标状态估计值),其中第7 s~第16 s因为目标信噪比较低,算法积累不够而未检测到目标,而第31 s却是因为粒子退化而出现的目标漏检;图5 TS-MMPF算法给出的估计目标存在概率不存在起伏,同时有效修补了第31 s出现的目标漏检,并给出了该时刻的目标状态估计,因此,本文算法可以有效地提供目标航迹信息,提高目标航迹的稳健性。
4 结论
为解决基于MMPF的TBD方法存在不能直接给出目标航迹,以及粒子严重退化时容易出现目标漏检等问题,提出一种基于TS-MMPF机动弱目标TBD算法。在对多目标进行检测跟踪时,往往需要知道各目标的航迹信息,即各时刻各状态估计值与前后时刻各状态估计值之间的关系,也就是状态值之间的关联问题,本文为基于PF类的TBD算法只能给出目标状态而不能给出目标航迹信息的问题提供了一种可行解决思路,下一步将针对该算法推广应用于多微弱目标的检测与跟踪情况,进一步增强算法的适应性。此外,如何有效缩短算法的积累时间,减小目标检测延滞也将是需要研究的难点问题。

