深化探究过程 培育核心素养——以人教版《13.4课题学习最短路径问题》为例

◎韦王莹

如何有效地将学生核心素养融入数学教学的过程中，本文尝试从初中数学课堂教学的维度，以人教版八年级上《13.4课题学习最短路径问题》为例，谈一谈基于初中数学核心素养的教学设计的实践。

一、创设有效情景奠基知识回顾

兴趣是学生学习的重要动力。为学生创设熟悉的生活情景，让他们经历将实际问题转化成数学问题的过程，可以激发学生的好奇心和探究欲望，唤醒学生现有的经验和认知，并引发思考活动。复习引入环节教学片断：

我们研究过一些关于“两点的所有连线中，线段最短”，“连接直线外一点与直线上各点的所有线段中，垂线段最短”等问题，这些问题可称之为最短路径问题。在现实生活中，我们会经常涉及到选择最短路径问题，因此，本节将利用数学知识探究数学史中著名的“将军饮马问题”。

设计意图：引入问题情境，激发学生学习和探究的兴趣

当学生学习新知识时，他们需要适当的原有知识和心智发展水平来进行学习。在这里创设情境，寻找与本节课有关联的旧知识点，可帮助学生建立新旧知识间的联系。学生在已有知识的支撑下，开始对新的知识产生疑问，从而迸发出思维的火花。教学不仅仅是在于传授知识，更在于激励与唤醒学生的学习动力。可见，创设有效情境，合理安排引入环节可以培养学生的数学意识，提高课堂教学有效性。

二、注重探究过程培养学生的核心素养

初中数学的六大核心素养有：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析。在初中数学教学中，核心素养是其重要的教学目标。但并非是每一节课都能体现出这全部的六大素养。那么在本节课中，我们可以培养学生的哪些核心素养呢？

1.借助层次性问题，培养学生数学抽象能力

问题1：从A地出发，到一条笔直的河边饮马，然后走到B地。请问到河边什么地方饮马能使所走的路线最短？

提问1、你能用自己的语言解释题目的含义，并把它抽象成数学问题吗？

活动1：学生独立思考，试着画图，看能否把A，B两地抽象为两个点，把河流抽象为一条直线问题。

提问2：假设在河上有任意一点C，我们说所走的路线指的是什么？

活动2：学生小组谈论，把点C与A，B连接起来，则AC＋BC的长度和指的就是要求的路线。

提问3：在河边饮马的地点有无数个，我们怎样才能在河上找出一个点，使得两条线段长度之和正好为最短的路线呢？

活动3：设C为直线上的一个动点，上面的问题就转化为：当点C在l的什么位置时，AC与CB的和最小（如图1）。

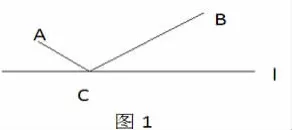
强调：将最短路径问题抽象为“线段和最小问题。

设计意图：通过步步追问，让学生将实际问题抽象为数学问题，即将最短路径问题抽象为“线段和最小问题”，不仅培养了学生用符号语言和图形语言表达数学问题的能力，同时有效地培养了学生的数学抽象能力。

2.画图操作，培养学生的直观想象能力

问题1：如图2，当点A、B分别在直线l的两边，如何在直线l上找出一个点，使得这个点分别到点A与点B的距离和最小？

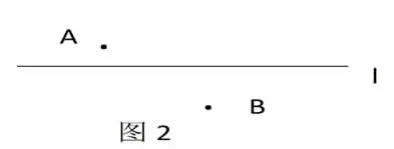
活动1：学生由“两点之间，线段最短”，可顺利找出点C。

问题2：如图1，如果点A，B在直线l的同侧，点C是直线上的一个动点，当点C在l的什么位置时，AC与CB的和最小？

追问3：对于问题2，是不是可以参照问题1，将点B“移”到l的另一侧B′处，满足直线l上的任意一点C，都保持CB与CB′的长度相等？

师生活动：学生独立思考，画图分析，小组交流，互相补充作法：（1）作点B关于直线l的对称点B＇；（2）连接AB＇，与直线 l相交于点C，则点C即为所求。

设计意图：通过搭建台阶，为学生探究问题提供“脚手架”，将“同侧”难于解决的问题转化为“异侧”容易解决的问题，渗透转化思想，同时培养学生的直观想象能力。

3.证明“最短”，发展学生的逻辑推理能力

提问1：能用所学的知识证明AC＋BC最短吗？

证明：如图，在直线l上任取一点C＇

（与点C不重合），连接AC＇，BC＇，B＇C＇。由轴对称的性质知，BC＝B＇C，BC＇＝B＇C＇.∴AC＋BC＝AC＋B＇C＝AB＇，AC＇＋BC＇＝AC＇＋B＇C＇.在△AC＇B＇中，AC＇＋B＇C＇＞AB＇，∴当只有在 C点位置时，AC＋BC最短。

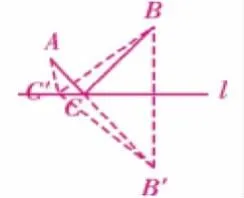
设计意图：让学生体会从画图到猜想，再到证明的学习过程，进一步提高他们的逻辑推理能力。

三、深化知识回顾，感悟转化思想

1.方法提炼提问

提问1：回顾本节课的探究过程，我们是通过怎样的过程、借助什么解决问题的？

提问2：轴对称在问题的研究中起到什么作用？

设计意图：通过反思，学生体验到轴对称的“桥梁”作用，感悟数学中经常用到的转化思想。在整个反思过程中，学生不仅能够还原整个知识的学习过程，还能将每个知识点还原到具体的问题情境，并且提出新的问题，自发地进行了全程性的反思。

如何在数学教学中培养学生的核心素养？我们教师要以数学知识为载体，通过创设生活情境，设计有层次性的问题，引导学生通过动手操作、证明猜想等多样化的学习活动，掌握数学双基，形成思维能力，并在运用数学知识解决问题的过程中培养创新精神和实践能力，从而实现核心素养的发展目标。