基于整距匝电势的相绕组电势表达式之推导

(华南理工大学电力学院，广东广州 510640)

0 引言

在导出交流绕组相绕组电势表达式时，传统电机学教科书[1～11]都是从一根导体的电势表达式出发的。这种方法基于磁场切割导体感生电势。法拉第电磁感应定律还有另一种表现形式，那就是e=-Ndφ/dt，即磁通变化感生电势。本文主要介绍这种方法。

说明：(1) 本文只讨论一对极基波情形。多对极及谐波情形不难类推。(2) 电动势简称为电势。(3)匝有时也称线匝。

1 短距匝和整距匝的电势

1.1 短距匝电势

当转子转到如图1所示位置时，转子基波磁场的分布图如图2所示。

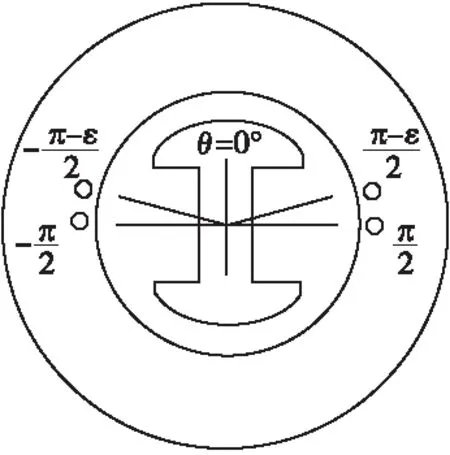
图1 短距线匝示意图

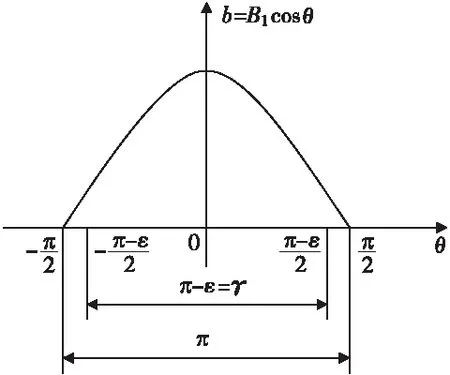
图2 基波磁场分布图

短距线匝的节距记为y，极距记为τ，短距线匝在定子内圆所张的电角度记为γ，易知

(1)

γ的补角记为ε，ε=π-λ。θ为沿定子内圆建立的电角度坐标，其原点位于磁极中心线。此时，穿过短距线匝的磁通达到最大值，记之为Φγ。穿过整距线匝的磁通最大值记为Φτ，取整距线匝的节距等于极距τ之意。显然，当γ=π时，Φγ=Φτ。

穿过短距线匝的磁通之瞬时值记为φγ，转子角速度记为ω，以图2所在瞬间作为时间原点，则有

φγ=Φγcosωt

(2)

下面计算Φγ

记定子内圆之半径为r，沿定子内圆积分的长度微分记为dx，则有

dx=rdθ

(3)

记定子铁心轴向长度为l，沿定子内圆积分的面积微分记为ds，则有

ds=ldx

(4)

穿过面积微分ds的磁通微分记为dφ，则由式(3)、式(4)两式知

dφ=bds=blrdθ

(5)

因极距长度为τ，故有

τ=πr

(6)

由式(5)、式(6)，参见图2，并计及式(1)，知

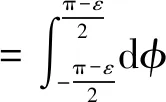
=Φτkp

(7)

式(7)中，引入了短距系数kp。

(8)

显然，短距系数与传统方法的无异。

以式(7)代入式(2)，得

φr=Φτkpcosωt

(9)

记短距匝电势为Et(有效值)、et(瞬时值)，t取turn(匝)之意。f为与角频率ω对应的时间频率。注意到匝数为1，由法拉第电磁感应定律可知

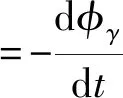
=ωΦτkpsinωt

(10)

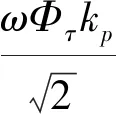
=4.44fΦτkp

(11)

1.2 整距匝电势

为了与短距情形区别，记整距匝电势为ET。当γ=π时，有kp=1，可知

(12)

显然，整距是短距的一种特殊情形。

2 线圈的电势

线圈的匝数记为Nc，线圈电势记为Ec，c取coil之意。由式(11)、式(12)易知

Ec=NcEt=4.44fΦτNckp

=ETNckp=ETNceff

(13)

Nceff=Nckp

(14)

式(13)中，Nceff是短距线圈折算到整距线圈时的匝数，可称为“短距线圈的有效匝数”，eff取effective之意。

3 线圈组的电势

线圈组的匝数记为Nq，线圈组电势有效值记为Eq，q取一个线圈组含q个线圈之意。槽距电角度记为α。分布系数记为kd。由传统的推导方法可知，

Eq=qEckd

(15)

以式(13)代入式(15)，可得

Eq=ETqNckpkd=ETNqeff

(16)

Nqeff=qNckpkd

(17)

式(16)中，Nqeff是由短距、分布线圈构成的线圈组折算到由整距、集中线圈构成的线圈组时的匝数，可称为“线圈组的有效匝数”。

4 相绕组的电势

相绕组的电势记为EΦ。相绕组的并联支路数记为a，支路匝数记为Nb，b取branch之意。支路匝数，传统称为“每相串联匝数”，意义含混。难道还有“每相并联匝数”不成？显然，没有。故本文特别提出“支路匝数”名称，以取代“每相串联匝数”。只是名称不同而已，所指的对象是相同的。

记相绕组总匝数为NΦ，绕组极对数为p。

对单层绕组言，NΦ=pNq。

对双层绕组言，NΦ=2pNq。

对单、双层绕组言

(18)

ks=1/a，a≥1，ks≤1。ks称为并联系数(s代表shunt，并联之意)，它表示与串联比较，并联引起相绕组电势计算匝数的减少。采用支路匝数时，相绕组电势为

EΦ=4.44fNbkpkdΦτ

(19)

将式(18)代入式(19)，得

EΦ=4.44f(ksNΦ)kpkdΦτ

=(4.44fΦτ)NΦkpkdks

=ETNΦeff

(20)

NΦeff=NΦkpkdks

(21)

式(21)中，NΦeff是考虑到短距、分布、并联三个因素后，计算相绕组电势时，折算到整距线匝的有效匝数，可称为“相绕组有效匝数”。

5 结语

5.1 基于整距匝电势ET，本文导出

(1)线圈电势表达式为

Ec=ETNceff

(22)

Nceff=Nckp

(23)

(2)线圈组电势表达式为

Eq=ETNqeff

(24)

Nqeff=qNckpkd

(25)

(3)相绕组电势表达式为

EΦ=ETNΦeff

(26)

NΦeff=NΦkpkdks

(27)

5.2 各电势表达式有一共同特点，都等于整距匝电势ET与相应的有效匝数之乘积，非常整齐。这显然具有美感，且还便于记忆。

5.3 各有效匝数表达式也有共同特点，都是实际匝数与相应系数的乘积，这些系数层层递进，与绕组的结构过程(短距、分布、并联)相对应，从kp到kpkd，再到kpkdks，同样具有美感，便于记忆。

5.4 本文的方法与传统电机学教科书的方法相比较，虽然两种方法都对，但是，本文的方法更有美感，更易于理解、记忆。