初步设计阶段倾转旋翼机短距起飞性能设计方法研究
齐万涛
(第一飞机设计研究院 总体气动设计研究所,西安 710089)
0 引 言
倾转旋翼机兼具直升机的垂直起降能力和固定翼飞机的高速巡航能力,使得该类飞机在抗震救灾和人道主义救援方面具有巨大优势。在复杂起飞场地环境下,倾转旋翼机可以无需借助跑道而进行垂直起飞;在场地条件允许的情况下,为了节省燃油、增加航程、执行起飞重量大于最大垂直起飞重量的起飞,亦可采用短距起飞的方式[1-3]。有多种方法可以帮助实现短距起飞,例如采用矢量推力和高升力襟翼、缝翼等[4]。倾转旋翼机的发动机短舱可以倾斜一定的角度,使得旋翼拉力产生一个前向的分量,该分量与常规飞机的推力或螺旋桨拉力的作用效果相同,使飞机加速到一定的起飞离地速度,该速度使飞机机翼产生足够的额外气动力并和旋翼拉力的垂向分量一起使飞机起飞离地。
大型民用倾转旋翼机在其概念设计阶段确定了起飞性能参数要求后,将转入初步设计阶段,其短距起飞离地速度、起飞场长等重要的起飞性能参数,与发动机短舱倾斜角密切相关。另外,当机场的海拔高度增加时,由于空气密度降低,起飞离地的真空速增加,加之发动机性能下降,导致倾转旋翼机的短距起飞性能降低。天气条件因素也可以影响发动机性能,进而对起飞性能产生影响。为了对上述影响起飞性能的因素进行分析,需要建立系统的倾转旋翼机短距起飞性能设计计算方法。短距起飞性能计算方法与固定翼飞机、直升机的起飞性能计算方法有很大区别。目前,国外对倾转旋翼机在初步设计阶段短距起飞性能设计计算方法的研究仍较少,迄今仅有“鱼鹰”及其衍生型等机型问世;国内的研究则更少[5-6]。朱源等[5]通过建立时变非线性纵向动力学模型并线化得到小扰动方程,而后对倾转旋翼机起飞轨迹进行了最优控制;严旭飞等[6]建立了适用于倾转旋翼机单发失效后轨迹优化的增广飞行动力学模型并进行了计算分析,对倾转旋翼机短距起飞单发失效着陆的轨迹进行了操纵优化研究。
本文针对影响倾转旋翼机短距起飞性能的因素,包括短距起飞短舱最小倾斜角、推重比、起飞离地速度、起飞距离等,进行了一系列研究,提出一套适用于初步设计阶段倾转旋翼机短距起飞性能的设计计算方法,并给出了计算结果。
1 短距起飞短舱最小倾斜角的确定
对于倾转旋翼机而言,空中飞行时,固定翼飞机模式下,发动机短舱和机身平行,此时短舱角度为0°;直升机模式下,发动机短舱和机身垂直,此时短舱角度为90°。在短距起飞地面阶段,旋翼桨的桨叶桨尖严禁触碰到地面并且应具有足够的安全距离,因此短舱倾斜角度受到相应的严格限制。
1.1 短距起飞短舱最小倾斜角的影响因素
CCAR-25-R4中规定,螺旋桨飞机,当飞机处于水平起飞姿态或滑行姿态时,对于前轮式飞机,螺旋桨桨叶与地面的安全距离均不得小于0.18 m[7]。由于倾转旋翼机短距起飞时类似于螺旋桨飞机,本文亦将该要求应用于倾转旋翼机。短距起飞短舱最小倾斜角几何限制如图1所示,γT为短距起飞短舱最小倾斜角,AB为短舱转动中心至旋翼桨毂中心距离,AE为桨叶长度,DE为桨尖距离地面的安全高度。
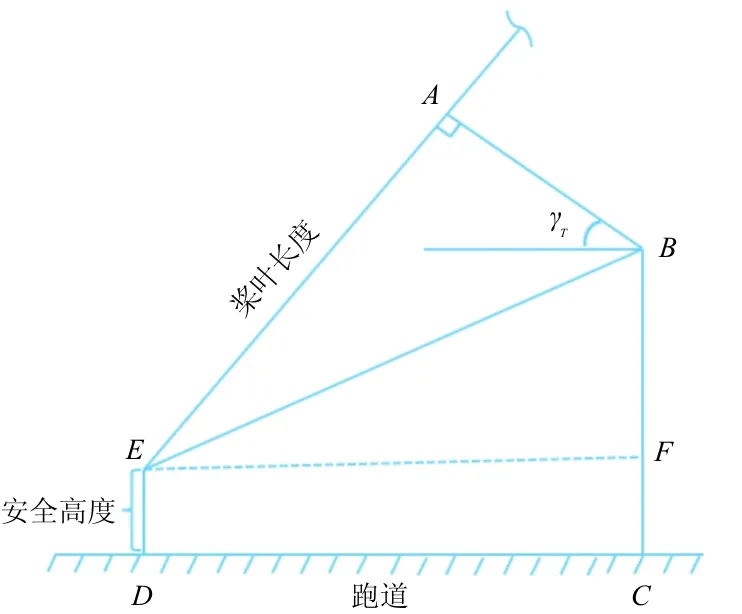
图1 短舱最小倾斜角几何限制示意图Fig.1 Geometry limitation of tilt angle
不同于传统的螺旋桨飞机,倾转旋翼机的旋翼一边转动一边挥舞,挥舞角β对桨尖安全距离的影响如图2所示。因此在确定短距起飞短舱最小倾斜角时,须考虑该因素。
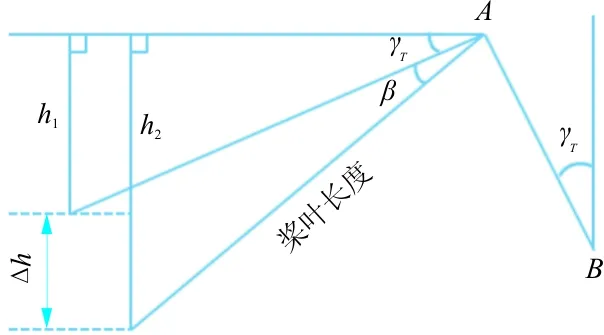
图2 挥舞角对桨尖安全距离的影响Fig.2 The influence of Conning angle on ground clearance
由图2可得,挥舞角引起的桨尖至地面距离的变化为
Δh=h2-h1=Rsin(γT+β)-RsinγT
(1)
式中:R为旋翼桨叶长度。
短舱转动中心距离地面的高度BC受机翼上反角、机身和起落架的影响,很难在初步设计阶段得到机身高度和起落架高度的最终值,因此需要考虑不确定因素对短舱最小倾斜角的影响。本文通过增大桨尖距离地面的安全高度来解决该问题。
1.2 短距起飞短舱最小倾斜角的计算分析
确定了该倾转旋翼机在初步设计阶段的几何参数后,根据几何限制约束(图1)和考虑了挥舞角引起的桨尖距地面距离的变化后,不同安全高度和挥舞角下的短距起飞短舱最小倾斜角的计算结果如表1所示。
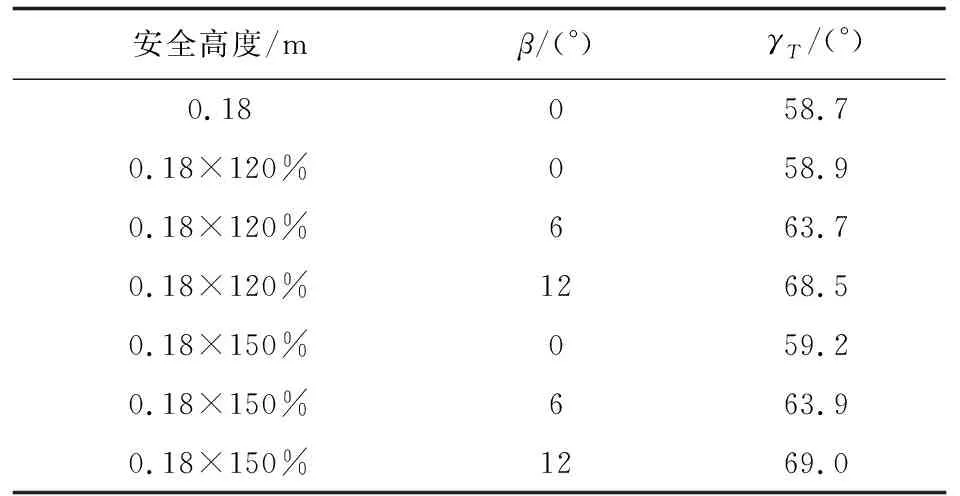
表1 不同安全高度和挥舞角下的短距起飞短舱最小倾斜角Table 1 Tilt angles of nacelle with the variation of ground clearance and conning angle
从表1可以看出:桨尖距地面安全高度的变化对短距起飞短舱最小倾斜角γT的影响较小,而挥舞角β的变化则对γT的影响较大。考虑到初步设计阶段起落架高度等参数的不确定性,在确定了桨叶挥舞角β后,短距起飞短舱最小倾斜角γT定为69°。该值为短距起飞几何限制值,即短距起飞地面阶段短舱倾斜角度严禁小于该值。
2 短距起飞性能计算方法
起飞性能的两个重要参数为起飞离地速度和起飞距离。起飞推重比和短舱倾斜角度对这两个参数起决定作用。
2.1 短距起飞推重比的确定
对于倾转旋翼机,垂直起降能力是一个基本要求,对应质量为2.5 g载荷条件下的最大起飞重量MTOW。依据文献[8],考虑了垂向机动和发动机功率提取等因素后,为了满足垂直起降要求,倾转旋翼机拉力和重力的比值,即推重比T/W在海平面应满足:
(2)
该要求通过发动机的选取和旋翼的设计来实现。
在高原机场以及高温天气,发动机性能降低导致推重比T/W急剧下降,另外由于起飞离地真空速增加,这些不利因素导致起飞距离大幅增加。
世界上尤其是我国境内存在众多高原机场。根据所选发动机的高度特性和温度特性,不同海拔高度和天气状况下推重比T/W的值如表2所示,ISA代表国际标准大气。其中最大计算高度为4 500 m,涵盖了世界上海拔高度最高的机场——四川稻城亚丁机场,其海拔高度为4 411 m。
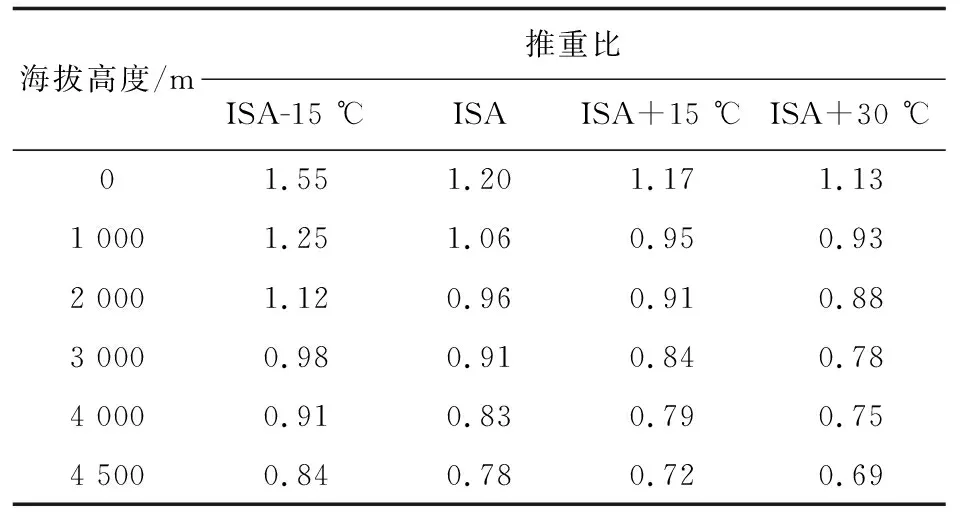
表2 不同海拔高度和天气条件下的推重比Table 2 Thrust to weight ratio in different altitudes and weather conditions
从表2可以看出:在最恶劣条件下,即机场海拔高度4 500 m和ISA+30 ℃天气状况下,推重比值由标准海平面的1.20降为0.69。
2.2 短距起飞离地速度和起飞距离计算方法
文献[9-11]仅给出了传统飞机起飞离地速度和起飞距离的计算方法。依据这些方法,本文推导了一系列适用于倾转旋翼机短距起飞方式的起飞离地速度和起飞距离的方程。
在地面滑跑阶段,包含了起落架支反力的运动方程:
Tsin(γT+α)+N+L=W
(3)
(4)
式中:T为旋翼拉力;α为起飞滑跑阶段飞机迎角;μR为飞机滑跑摩擦系数;N、L和D分别为起落架支反力、飞机升力和阻力。
在起飞离地点,起落架支反力为零,依据该条件,首先确定起飞离地速度VLOF:
(5)
式中:CL为起飞离地时的升力系数,由起飞离地迎角确定;ρ、S分别为大气密度和机翼参考面积。
然后经过推导,可得地面滑跑距离SG计算公式:
(6)
(7)
(8)
式中:g为重力加速度;CD为飞机阻力系数。
根据能量法,起飞空中距离SA可表示为
(9)
式中:V2为起飞安全速度;下标av表示起飞离地点和起飞安全高度点的平均值。
短距起飞距离Stf为地面滑跑距离SG和起飞空中距离SA之和,即:
Stf=SG+SA
(10)
3 短距起飞性能计算结果及分析
起飞重量对飞机起飞性能有重要影响,本文选取飞机最大短距起飞重量进行计算,该重量约为飞机最大垂直起飞重量的1.1倍。
给定飞机推重比后,根据上述所得到的短距起飞距离公式,计算不同短舱倾斜角度的起飞距离,计算结果如图3所示,虚线为几何限制条件下的短舱最小倾斜角。
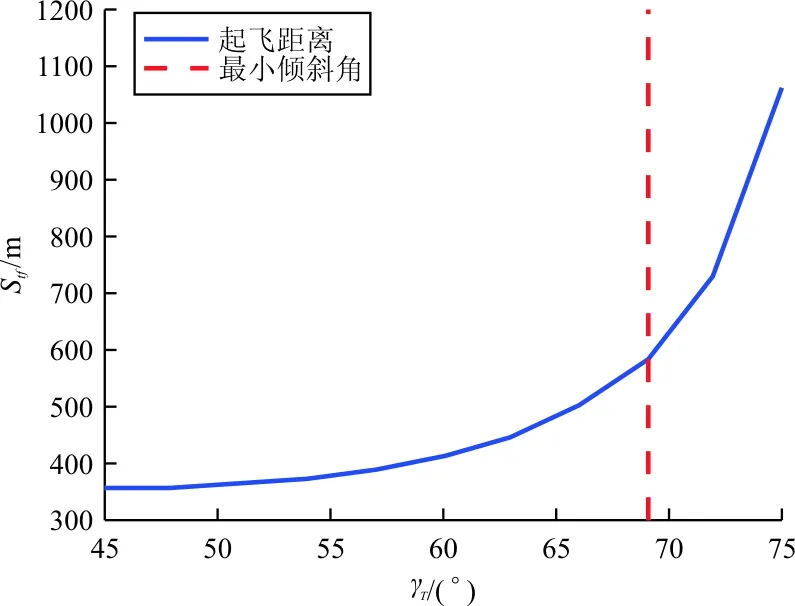
图3 不同短舱倾斜角起飞距离Fig.3 Take-off distance of different nacelle tilt angles
从图3可以看出:随着短舱倾斜角度的增加,起飞距离增加。但因为短舱倾斜角受桨尖至地面安全距离的限制,故取该限制条件下的短舱最小倾斜角的值为69°,以取得最小的起飞距离。
机场海拔高度和天气条件对短距起飞性能亦有重要影响。海拔高度和天气条件会影响飞机的推重比(如表2所示)。给定短距起飞短舱倾斜角度69°后,不同机场海拔高度和推重比下的短距起飞离地速度和起飞距离可根据式(5)~式(10)计算得到,计算结果如图4~图5所示。
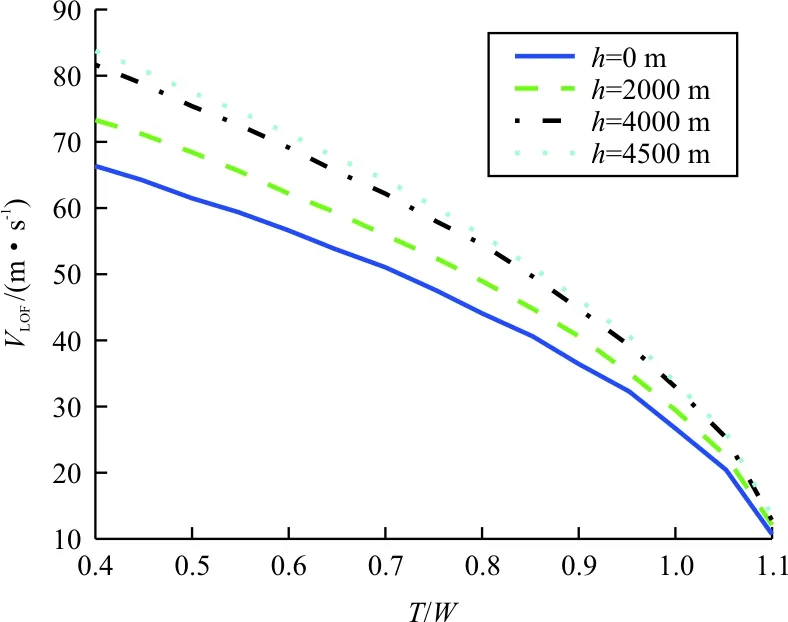
图4 不同机场海拔高度和推重比下的起飞离地速度Fig.4 Lift-off speed of different altitudes and thrust to weight ratio
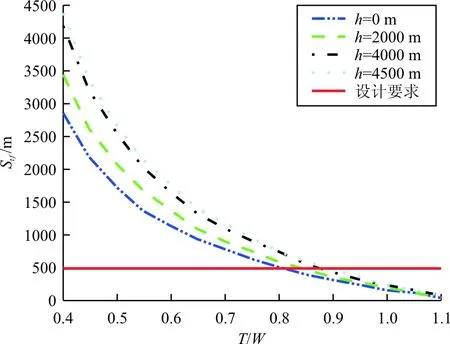
图5 不同机场海拔高度和推重比下的起飞距离Fig.5 Take-off distance of different altitudes and thrust to weight ratio
从图4~图5可以看出:发动机短舱倾斜角为69°时,起飞离地速度随着推重比的增加而减小,随着海拔高度的增加而增加;起飞距离亦表现出同样的规律;图5中平直线为短距起飞距离设计要求,该值应不大于500 m,为了满足该要求,在海平面和4 500 m高度,推重比需分别大于0.81和0.88。从表2可以看出:在海平面不同天气条件下,推重比均大于0.81,起飞距离满足设计要求。而在高原机场,飞机发动机性能恶化,导致推重比下降较快,部分计算点起飞距离不能满足设计要求。考虑到高原机场拥有较长的跑道,这种情况是可以接受的。
对于飞行来说,机组人员首先应根据机场高度和天气状况从表2中确定飞机的推重比,再依据推重比和海拔高度的关系从图4~图5中确定飞机的起飞离地速度和起飞距离,然后以起飞离地速度操纵飞机完成离地。对起飞离地速度的确定亦可由飞控计算机来完成。
4 结束语
本文通过对倾转旋翼机短距起飞性能的研究,提出了一套适用于初步设计阶段倾转旋翼机短距起飞方式的起飞性能设计方法。使用该方法得出的倾转旋翼机短距起飞性能计算结果合理,具有很好的工程应用价值。

