基于改进遗传算法的突防突击航线规划
李涵,姚登凯,赵顾颢
(空军工程大学 空管领航学院,西安 710051)
0 引 言
在现代战争中,歼轰机突防突击是航空兵有效的进攻手段,可以起到出其不意杀伤敌人的效果,因此合理规划我方突防突击航线,有效减少我方战机的被击落概率对保证任务成功和人员安全具有重要作用。
针对突防突击航线的规划问题,国内已有研究人员对其进行了不同方面和程度的研究。段海滨[1]对蚁群算法进行了详尽总结;柴毅哲等[2]在此基础上对蚁群算法做出了一定改进,综合分析了影响飞行的各类因素,提出了可规避威胁源的航线规划方法;饶卫平等[3]、Peng Zhihong等[4]提出了基于多智能体遗传算法的无人机突防航线规划方法;刘光宏等[5]利用进化算法规划了和导弹轨迹相关联的测量飞机航线的方法;汪先超等[6]、刘波等[7]规划了多普勒盲区下的低空突防航线;张帆等[8]、米粮川等[9]利用多准则遗传算法进行了最短路径的航线规划。上述研究多考虑影响飞行的因素,包括天气、地形、威胁源等,所规划的航线通常是精确但较为复杂的,有人机执行起来相对困难。而且,对突防突击飞机安全的重要影响因素之一是敌方空中和地面火力的拦截,上述研究缺少对航线中飞机被敌火力击落概率的研究和分析。
国外,亦对航线规划的方法进行了研究和创新,例如,提出了Voronoi图法[10]应用于战术飞行规划,以及用于搜索最优航线的模拟退火算法[11]和粒子群算法[12]等。在众多方法中,遗传算法因其自身隐含的并行性和多目标优化特点,已被广泛研究和使用。
对于本文所研究的突防突击航线规划问题,其适应度函数较为复杂,传统遗传算法的二进制编码及遗传操作容易产生不可行解,致使搜索效率大幅降低,因此,本文需对传统遗传算法进行改进。首先分别对敌地面火力和空中火力击落我方飞机的概率进行建模和分析,然后利用本文改进的遗传算法,搜索被击落概率最低的突防突击航线方案。
1 击落概率分析建模
1.1 建模前假设
(1) 突防突击任务可简化为两段,一是突破敌方拦截飞机,由出发点至进入敌地面火力范围;二是突破敌方地面防空火力,由进入敌对面火力范围至突击目的地。
(2) 假设敌只有一批巡逻飞机,位置已知并固定,防空导弹阵地雷达位置已知。
(3) 敌巡逻飞机仅在地面火力范围以外展开截击。
(4) 制空战斗机采用导弹先中距弹、后近距弹、再航炮的方式实施攻击,且航炮最多发射4次。
(5) 挂载方式为2中距、2近距,假设中距弹、近距弹以及航炮的击落概率相等。
1.2 击落概率分析
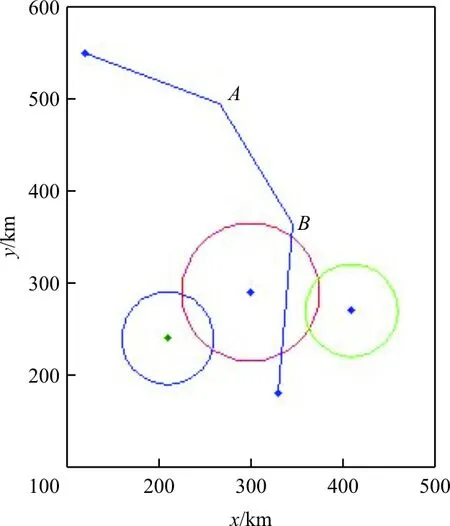
设起始点为O点,目标点为T点,圆表示敌地面防空火力在突防突击高度上的范围,从左至右依次标记为O1,O2,O3,且O1和O3的半径为50,O2的半径为75。各点坐标为O(120,550)、T(330,180)、O1(210,240)、O2(300,290)、O3(410,270)。过O、T两点分别作OT连线的垂线,在两条平行线中间取两点A、B,使得OA、AB、BT三段航线之和不超过飞机的最大作战半径,则O-A-B-T为突防突击航线。各点分布如图1所示,若航线经过导弹阵地火力范围,则与圆的交点为C1,C2,…,Cn。规定敌巡逻飞机位置的坐标为(150,380),敌地导阵地里雷达的坐标(从左至右)依次为:(200,220)、(240,230)、(290,250)、(340,260)、(390,240)、(440,250)。

图1 各点分布示意图Fig.1 Points distribution map
1.2.1 预警雷达系统发现飞机概率
根据文献[13]建立雷达探测概率模型,利用雷达虚警概率、某高度上探测概率为0.5的威力曲线(即此高度上探测概率为0.5的探测距离)、目标与雷达之间的距离计算概率。
假设高度为h处某方向探测概率为0.5的威力半径为Srn_0.5,该高度某点与雷达的距离为Srn,可根据式(1)计算该点位置处较探测概率为0.5位置处的等效脉冲信噪比增加的分贝数。
(1)
探测概率、虚警率与等效单脉冲信噪比的关系如表1所示,Pr_i为第i部雷达预警发现概率;Pfa为虚警率;U为等效单脉冲信噪比。令探测概率小于0.3时,计该点处的探测概率为0;探测概率大于0.9时,计为1。将增加后的分贝数对照表1,即可查得该点处的预警发现概率。

表1 探测概率、虚警率与等效单脉冲信噪比的关系Table 1 Relationship of detection probability, false alarm rate and equivalent single pulse signal to noise ratio
假设某雷达在虚警率为10-6时,探测概率为0.5的等效脉冲信噪比为12.5 dB,高度为h的探测距离为220 km,设E点在雷达所处平面内的投影距离雷达160 km,高度为h,则增加的信噪比为Δ=40lg(220/160)=5.5。则E点处的等效脉冲信噪比为(12.5+5.5) dB。查表得,预警发现概率约为0.8+0.1×(18-16.6)/(19.8-16.6)=0.84。
根据上述模型,某一点处被雷达网探测发现的概率为
(2)
式中:n为雷达数量。
1.2.2 被敌地面火力发现后击落概率
如果飞机飞入敌地面火力范围内,则计算飞机的航迹与每个圆之间的相对关系,若穿过圆k,则计算在圆k中能被炮击的最大次数:
(3)
式中:VT为突击编队飞机速度,单位是km/h;t1为导弹两次发射间隔,单位是h。
设每一次地面射击飞机被击落的概率均为80%,则编队被第k个导弹阵地击落的概率Pdk为
Pdk=1-(1-0.8)Qk
(4)
则在圆内飞行时被击落概率Pd为
(5)
1.2.3 被敌拦截飞机击落概率
根据截击作战特点,在敌方预警探测系统发现我方突击编队以后,立即按照截击三角形对我机进行拦截。截击三角形几何关系如图2所示,VF为敌拦截飞机飞行速度,单位是km/h;t2为我方飞机飞行时间,单位是h;t3为中距导弹飞行时间,单位是h;t4为效果评估加上再次锁定目标需要时间,单位是h;t5为近距导弹飞行时间,单位是h;t6为一次航炮攻击所需时间,单位是h;ST为我方飞机被敌机发现后飞行至地面火力范围的距离,单位是km;Nhp为航炮设计次数;L为敌机发现我机时两者的距离,单位是km;H为敌机距OB连线的距离,单位是km;φ、θ分别为截击三角形中的角度参数,单位是rad。

图2 截击三角形示意图Fig.2 Truncated triangular diagram
截击机发射中距弹后,突击编队移动距离为VTt2,假设期间突击编队采用除机动以外的各种干扰手段进行对抗,或仅进行短时间的机动躲避以后立刻回到航线上,则这一阶段每架突击飞机被击落的概率为
Pzj=1-(1-Pr_jq)kuz
(6)
式中:Pr_j为被敌机雷达发现的概率,可由1.2.1中计算雷达发现概率的原理得出;q为被一枚中距导弹击落概率;k为敌机架次;uz为发射中距导弹的数量。
截击机会对打击效果进行评估,再进行近距弹的锁定,所需时间为t3。
敌机发射近距弹和航炮的流程同上,可得被近距导弹击落概率Pjj和被航炮击落概率Php为
Pjj=1-(1-Pr_jq)kuj
(7)
Php=1-(1-q)kuhp
(8)
式中:uj为发射近距导弹的数量;uhp为航炮攻击次。
针对我方飞机在被敌机预警系统发现后飞行的距离需要进行判定:
(1)ST≥VT×(t2+t3+t4+t5+4×t6)时,敌机完成所有拦截攻击。
(2)VT×(t2+t3+t4+t5+m×t6)≤ST (3)VT×(t2+t3+t4)≤ST (4)VT×(t2+t3)≤ST (5)ST 又根据正弦定理可得: (9) 综合得到被敌机发现后击落的概率Pj为 Pj=1-(1-Pzj)(1-Pjj)(1-Php) (10) 1.2.4 整体击落概率 实际航线是连续的,为了便于计算将其离散化。在OAC1段航线中,从O点开始,每间隔5 km(不足5 km的舍去)取一点作为有效发现点,即在这些点才允许被敌机雷达系统发现,分别记为1,2,3,…,i。将每一点分别作为被敌机发现位置并计算被发现概率Pji,那么在OAC1航段被敌机击落的概率PJ为 (11) 式中:doac为OAC1航段的长度,单位是km。 在C1BC2段航线,从C1点开始每间隔5 km(不足5 km的舍去)取一点作为有效发现点,分别记为1,2,3,…,j。计算每一点我机被发现概率Pr_dj,则在敌地面火力范围内被雷达系统发现的概率Pr_D为 (12) 式中:dcbc为C1BC2航段的长度,单位是km。 则被敌地面火力击落的概率PD为 PD=Pr_DPd (13) 综合两段航线得出整条突防突击航线被击落概率P: P=1-(1-PJ)(1-PD) (14) 遗传算法是模拟达尔文“进化论”思想的一种全局寻优算法。该算法通过对种群中个体进行编码、选择、交叉、变异等操作,对种群进行更新直至结束条件,最终得到最优解。算法基本流程如下: 步骤1 确定遗传代数N,一般为100~150。随机生成初始种群并对种群中每个个体进行二进制编码,种群大小n一般为30~160。 步骤2 计算每个个体的适应度函数值f,然后随机选择两个个体进行遗传操作。 步骤3 以概率ρ对两个个体的基因片段进行交叉,产生两个新个体交叉概率一般为0.25~0.75。 步骤4 新个体每一个基因有δ的概率进行变异,即“0-1互换”,产生新的个体。 步骤5 判断是否满足结束条件,是则选择最优个体输出,否则返回步骤2。 对于连续变量二进制编码具有严重缺陷,通常会在目标函数中引入附加的多峰性,从而使编码后的目标函数比原始问题更加复杂。而选择交叉个体时采用的随机选择方法,缺少进化的方向性,容易产生不可行解。这两方面都大幅增加了搜索成本,不适用于本文要解决的问题,故需要对其进行改进。 分别从选择和交叉变异两个操作步骤对其进行综合改进,并结合实数编码,克服传统遗传算法在本文应用中的局限性。 2.2.1 种群预处理 步骤1 种群初始化 在靠近O点一侧随机取一个A点,靠近T点一侧随机取一个B点,连接O-A-B-T为一条航线,即一个个体,共选取125个个体组成初始种群。 步骤2 实数编码 突防突击航线是由O、A、B、T四个点组成的,起始点O和目标点T都是固定点,在交叉和变异中不产生变化,因此只对A点和B点进行编码。对连续变量二进制编码具有严重缺陷,通常会在目标函数中引入附加的多峰性,从而使编码后的目标函数比原始问题更加复杂,故采用实数编码。将A、B两点的横纵坐标按顺序排列得到的向量,即个体的基因。例如,A(400,221),B(441,309),则此个体的编码为向量(400,221,441,309)。 2.2.2 遗传优化 步骤3 选择策略 赌盘选择是最常见的策略,该方法虽然简单易懂、便于操作,但容易导致“早熟”的缺点。使用约束的最优保存策略[14], 可以有效防止“早熟”的发生。最优保存策略即当前群体中适应度最优的个体不参与交叉和变异运算, 而是用来替换掉本代种群经过交叉、变异等操作后产生的新种群中适应度最差的个体。首先根据击落概率模型计算出每一个个体被击落的概率,作为适应度值,选择最小的作为最优个体保存至下一代,其余个体参与遗传优化进入下一代;然后用父代中适应度最小的个体代替子代中适应度最大的个体产生新种群。 步骤4 可变算术交叉 算术杂交的理念源自凸集理论[15]。一般地,由向量x1和x2的加权平均得到的x3为 x3=λ1x1+λ2x2 (15) 如果限制乘子: λ1+λ2=1 (λ1>0,λ2>0) (16) 则称为凸组合,杂交类型为凸杂交。如果乘子不符合非负的条件,则称之为仿射组合,杂交类型为仿射杂交。如果乘子可取任意实数,则称之为线性组合,杂交类型为线性杂交。 因此定义杂交后的个体为 (17) 为了避免遗传操作后的个体大量出现在解空间之外,采用凸杂交[16]。每一代遗传中乘子在[0,1]中随机变化,可以增加个体被破坏的程度以及种群多样性,提高搜索效率。 经过150代遗传之后得到新种群,根据仿真结果,适应度最小的个体的路径为O(120,550),A(226.2,495.7),B(345.8,364.3),T(330,180),此时被击落概率为0.019 3。仿真结果如图3所示。 图3 仿真结果Fig.3 Simulation result 从图3可以看出:A、B两点都位于敌地面火力范围之外,且相对远离有敌拦截飞机巡逻的一侧。 通过20次仿真得到各个局部最优解,如表2所示。 表2 各个局部最优解Table 2 The local optimal solutions 从表2可以看出:由于初始种群的不同,以及仿真次数的限制,每一次仿真结果可能略有差异,因此并不能确定被击落概率为0.019 3的方案是全局最优解;经过20次反复仿真,得到的概率为0.019 3方案的次数最多;对于突防突击航线来说,不要求经纬度十分精确,且表中概率相近,因此选取被击落概率为0.019 3的航线作为最终规划方案,可以满足安全需要。 本文提出了基于改进遗传算法的突防突击航线规划方法。将被击落概率作为适应度函数,选择策略采用带约束的最优保存策略,提出可变算术杂交算子,增加种群多样性以防止陷入局部最优,同时,也极大地减少了产生不可行解的概率。经过模拟仿真,150代迭代计算之后,得到的最优解为由O(120.0,550.0)、A(226.2,495.7)、B(345.8,364.3)、T(330.0,180.0)四个点组成的航线。此方法规划的航线可以减小飞行员的操作难度,提高安全性,满足参谋人员决策需求,适应现代化作战需要。 本文不足之处在于,计算被击落概率模型仅考虑了敌机和敌地面防空火力两个因素,模型尚不完善,下一步工作中需要进行更加全面的研究。2 基于改进遗传算法的航线规划
2.1 传统遗传算法
2.2 改进的遗传算法
3 仿真结果分析

4 结 论

