基于车辆变道影响的城市路段交通流模型研究
邓社军, 钟煜一, 叶晓飞, 陈 峻, 白 桦
(1. 扬州大学 建筑科学与工程学院,江苏 扬州 225009; 2. 宁波大学 海运学院,浙江 宁波 315211;3. 东南大学 交通学院,江苏 南京 210096; 4. 中设设计集团股份有限公司,江苏 南京 210096)
0 引 言
换道是城市交通常见的驾驶行为,其涉及驾驶员的感觉、知觉、判断、操作等诸多交通特性。当交通流密度较低时,换道有利于驾驶员获得期望的行驶速度,提高道路交通的运行效率;而当交通流密度较高时,换道机会减少,若强行换道则会影响当前车道和目标车道的行驶速度,容易产生交通冲突,形成交通安全隐患[1]。
目前国内外主要采用交通仿真和试验数据的分析方法,研究在不同换道行为决策、变道安全距离和换道次数等情形下的换道模型[2-4],而针对车辆换道对道路交通流影响模型的研究成果尚不多见,相似的研究主要体现在车辆换道对道路交通的干扰影响方面。敬明等[5]分析了满足换道条件的车辆数与车辆密度的关系;魏丽英等[6]引入公交车影响因子,运用元胞自动机模型分析了公交车对社会车辆换道行为的影响;S.OH等[7]调查了多种交通状态下的交通流,发现换道行为虽然可以提高目标车道的流量,但最终会影响影响交通流运行效率,降低路段下游的通行能力;徐慧智等[8]基于实测数据,构建了换道行为对交通流运行速度的影响模型;禹伟[9]利用交通波模型和加速度模型定性分析了换道与交通拥挤的关系;王茉莉[10]建立了基于模糊控制理论的车辆换道模型,并通过了仿真对比,量化分析了车辆不同换道次数对交通流的影响。车辆在换道的过程中,不同的变道加速度、安全换道距离和相邻两车道的不同车流状态等,均会导致换道车辆对目标车道造成不同的影响[11-12],而已有的研究更多侧重于道路交通流的宏观变化特性,缺少对变道影响时间的分析,尤其是缺少多因素耦合作用下各车道车流的微观变化特性分析。
在已有研究的基础上,基于车辆换道的安全距离特性,通过理论分析得出了换道影响时间的计算模型,结合实例建立了城市道路单个车道在换道影响下的车流速度动态变化模型,并进行了仿真模拟验证,对于进一步研究主路交通安全和延误的变化特性具有一定的现实意义。
1 车辆变道安全距离特性分析
为了研究变道对目标车道社会车辆的影响程度,笔者通过分析车辆变道的过程及变道车辆的行进轨迹,通过理论的方法寻找相关特性与规律。由于主要研究换道对目标车道车辆的影响,因此不考虑变道车辆与本车道前后车的距离。为了便于统一研究,笔者确定了车道编号规则,即最靠近道路中心线的车道为1,依次向外侧方向编号分别为2、3。图1为换道前车道1与车道2各车辆的位置,为了便于分析车辆的行进轨迹,以变道车辆的最左边缘为横坐标轴,向上为纵坐标轴,建立坐标系。图1中:O为车道1的换道车辆,C为换道车辆前车,D为换道车辆后车,A为目标车道的前车,B为目标车道的后车;WO为换道车辆的车宽,WA为目标车道前车的车宽,W1为换道车辆最左侧与目标车道前车最右侧的距离,W2为换道车辆最左侧与目标车道前车最左侧的距离,W3为目标车道的宽度;LA为目标车道前车的车长,LO为换道车辆的车长,O1为换道车辆的左前角点。
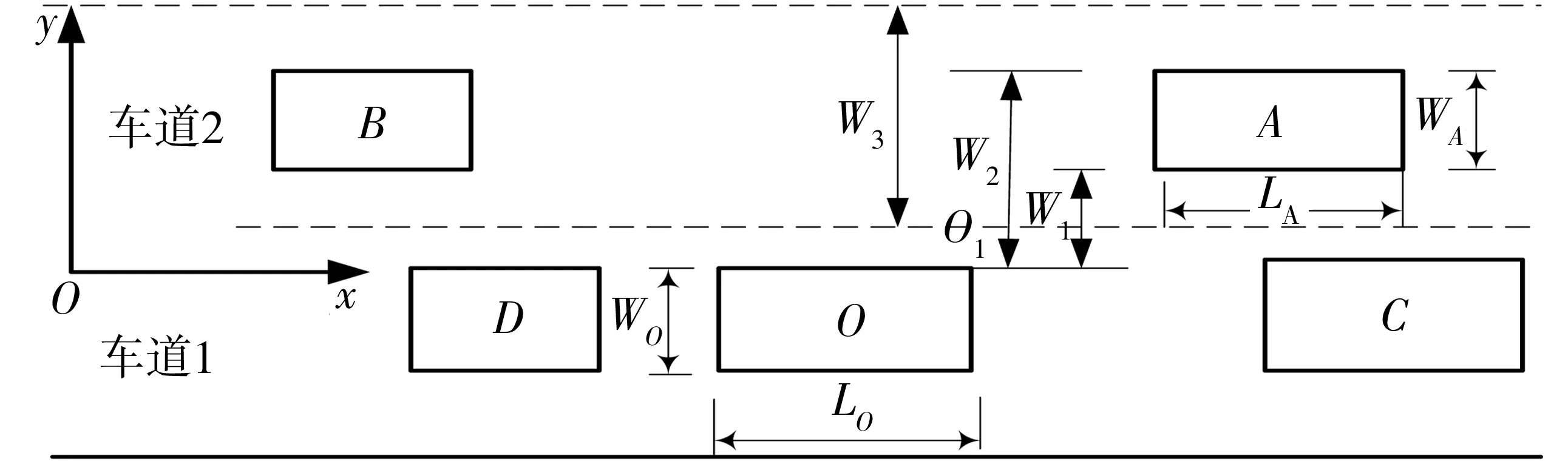
图1 车辆换道前的各车位置Fig. 1 Initial position of the vehicles before lane change
1.1 变道车辆与目标车道前车安全距离特性分析
由于小客车是城市交通的重要组成部分,因此仅针对此类型车辆的换道特性进行研究。图2为变道车辆与目标车道前车的运动轨迹示意。
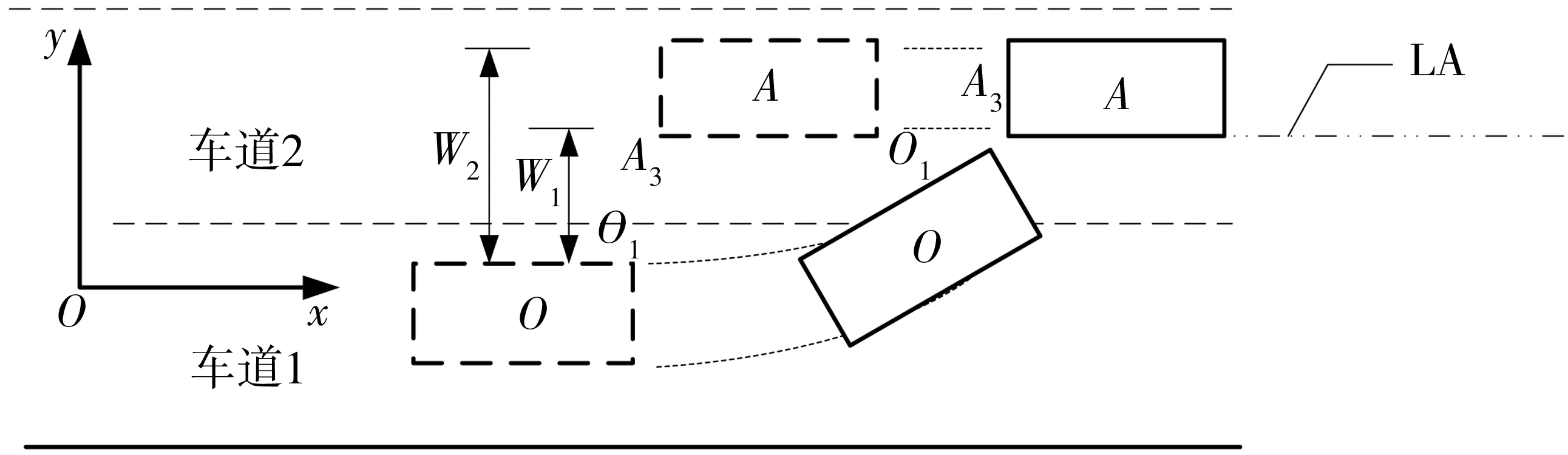
图2 变道车辆和目标车道前车的运动轨迹示意Fig. 2 Trajectory of the lane-change vehicle and the front vehicle on target lane
为了描述车辆变道后与目标车道前车与后车的关系,根据建立的坐标系,假设在任意t时刻,变道车辆的横、纵坐标分别为xO(t)、yO(t),目标车道前车A的横、纵坐标分别为xA(t)、yA(t)。假设变道车辆O左前角O1接触到车道2与车道1的车道分界线的时刻为tadj+tc,其中,tadj为开始侧向加速的时刻,tc为车辆开始侧向加速后的持续时间。在tadj+tc时刻,变道车辆左前角O1越过车辆A最右侧的水平线LA,并假设与该线交于C点,则tadj+tc为变道车辆行驶到C点的时间。则有:
(1)
式中:θ(t)为变道车辆O在tadj+tc时刻与水平方向的夹角,其值可以计算得出:
(2)
将w2=yA(tadj+tc),w1=yO(tadj+tc)代入式(1),则有:
(3)
当t≥tadj+tc时,变道车辆越过LA线,容易与A车发生侧面碰撞事故;当车辆完成变道后,则容易与A车发生追尾事故。因此在T≥t≥tadj+tc时,为变道车辆的危险时段。要使得两车不发生碰撞,则需满足:
(4)
令变道车辆左前点O1与目标车道前车A右后点A1的水平距离为S(t),则有:
vO(0))t+SAO(0)=SA(t)-LA-wO.sin[θ(t)]-
SO(t)+SAO(0)
(5)
式中:SAO(0)为车辆变道的初始时刻变道车辆O车头与目标车道前车A的车尾的初始纵向距离。
因此,要使得变道车辆没有碰撞,则必须S(t)>0且SAO(0)满足最小安全距离要求,即:[13]
(6)
1.2 变道车辆与目标车道后车安全距离特性分析
同样,为了为避免发生摩擦或碰撞等,车辆在变道后亦必须保证变道车辆与目标车道后车辆之间最小的安全距离,两者的位置关系见图3。
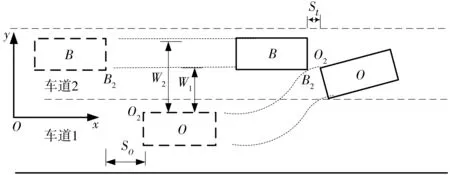
图3 变道车辆和目标车道后车的运动轨迹示意Fig. 3 Trajectory of the lane-change vehicle and the rear vehicle on target lane
令变道车辆左后点O2与目标车道后车B右前点B2的水平距离为S(t),则有:
vB(0))t+SBO(0)=xO(t)+LOcos[θ(t)]+wO·
sin[θ(t)]-xB(t)+SBO(0)
(7)
式中:SBO(0)为车辆变道的初始时刻变道车辆O的车头与目标车道后车B的车尾的初始纵向距离。
因此,要使得变道车辆与目标车道后车不发生碰撞,则必须S(t)>0且SBO(0)满足最小安全距离要求,即:
(8)
2 车辆变道影响时间分析
2.1 车辆变道时间
相关研究表明[14],每一名驾驶员在特定交通流密度下都有一定期望车速,该期望车速与车辆机械性能、驾驶员特性、道路的限速措施等有关。当车辆在当前车道行驶时,由于受到前方慢车的影响而使其车速低于期望车速的一定数值范围内,则车辆会产生变道的意图,由于车辆变道通常是由车速较低的车道换入车速较高的车道,因此笔者主要针对这种类型开展研究。
由式(8)分析可知,要计算变道车辆与目标车道车辆之间的安全距离,则需测定车辆之间的速度与加速度。由于在实际测量中难度较大,因此假设在变道的过程中,变道车辆以恒定加速度行驶,其它车辆保持匀速运动。
2.1.1 变道车辆与目标车道前车的变道时间
此时的变道时间即为变道后能与前车保持最小安全距离的时间。图2为变道车辆O与目标车道前车A的运动轨迹。假设车辆变道开始的时刻为t0,变道结束后的时刻为t1,变道时间为ta,则ta=t1-t0。车辆在加速变道完成后,其速度与目标车道的车速保持一致,即vO(t)=vA(t)。则车辆的变道加速时间为:
(9)
式中:aO为车辆换道的加速度,m/s2;vA为车辆换道后的速度,m/s;vO为车辆换道前的速度,m/s。则在ta时间内变道车辆O行驶距离:
(10)
在ta时间内目标车道前车A行驶距离SA=vA·ta=vA(t1-t0),则变道车辆O与目标车道车辆A在变道后的纵向水平距离:
(11)
若变道车辆O能够不与目标车道车辆A发生碰撞,则必须S(t)>0,即
wOsinθ(t)>0
(12)
求解式(12),得出:
t1,2={(vA-vO)±[(vA-vO)2+2aO(SAO(0)-
wOsinθ(t))]1/2}/aO
(13)
{(vA-vO)-[(vA-vO)2+2aO(SAO(0)-
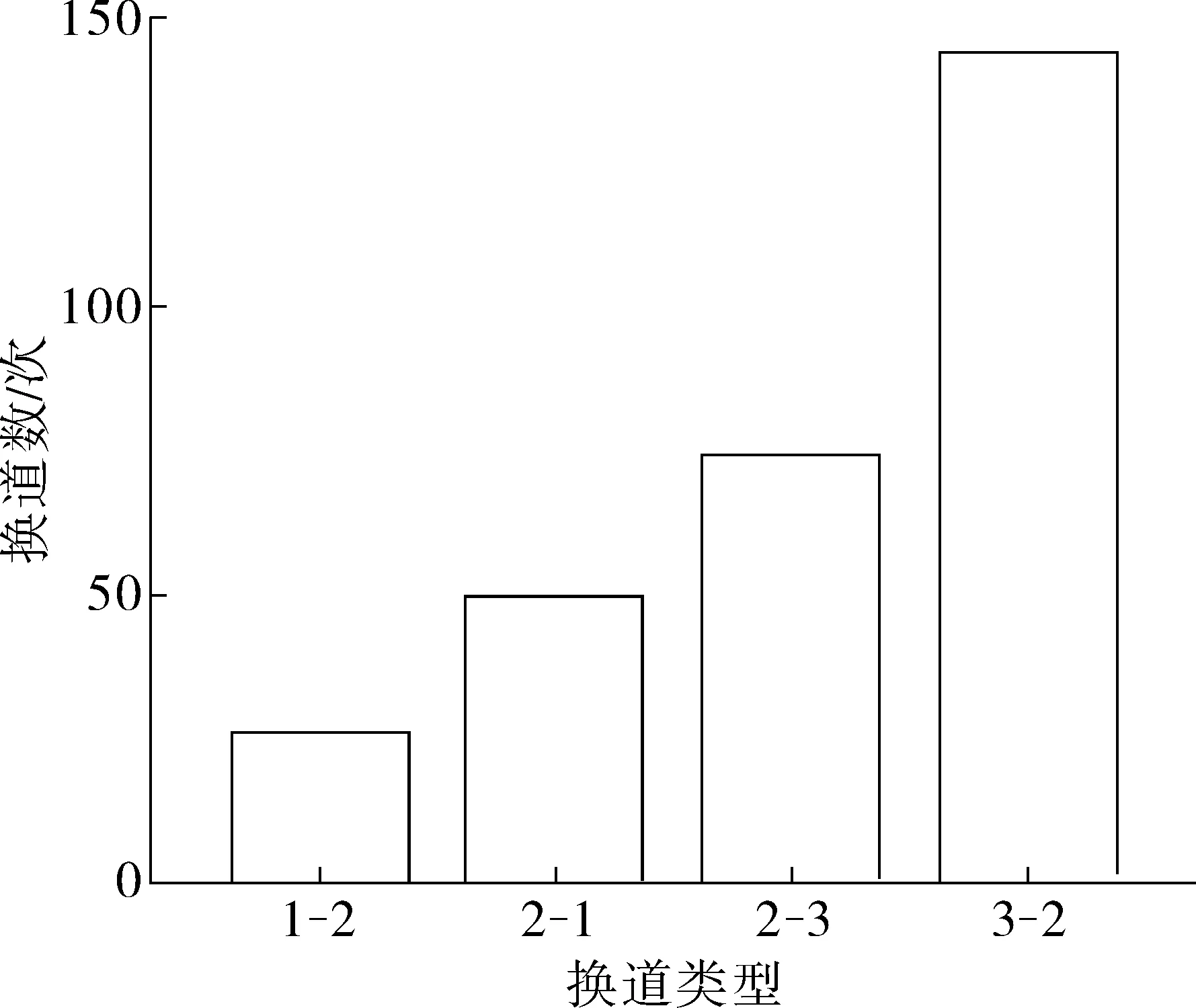
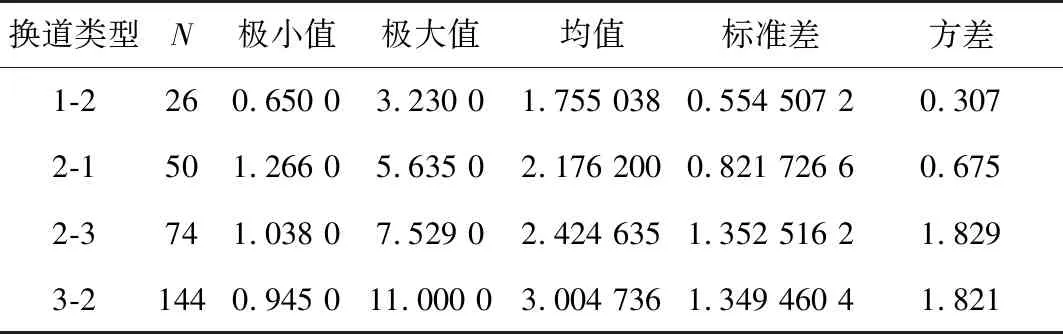
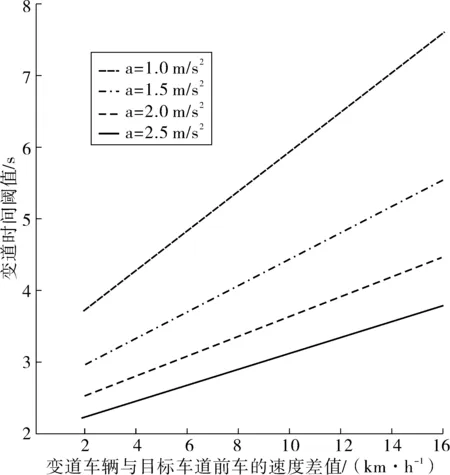
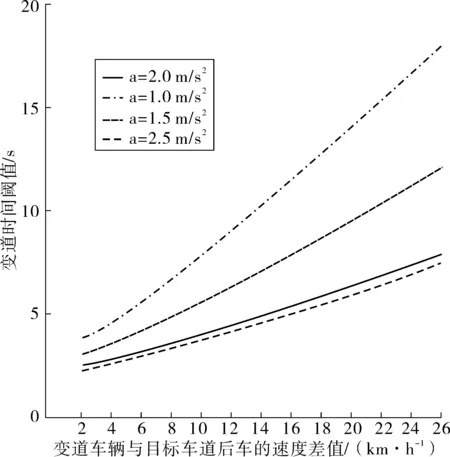
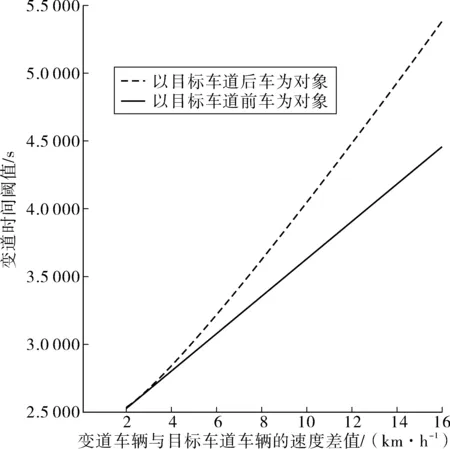
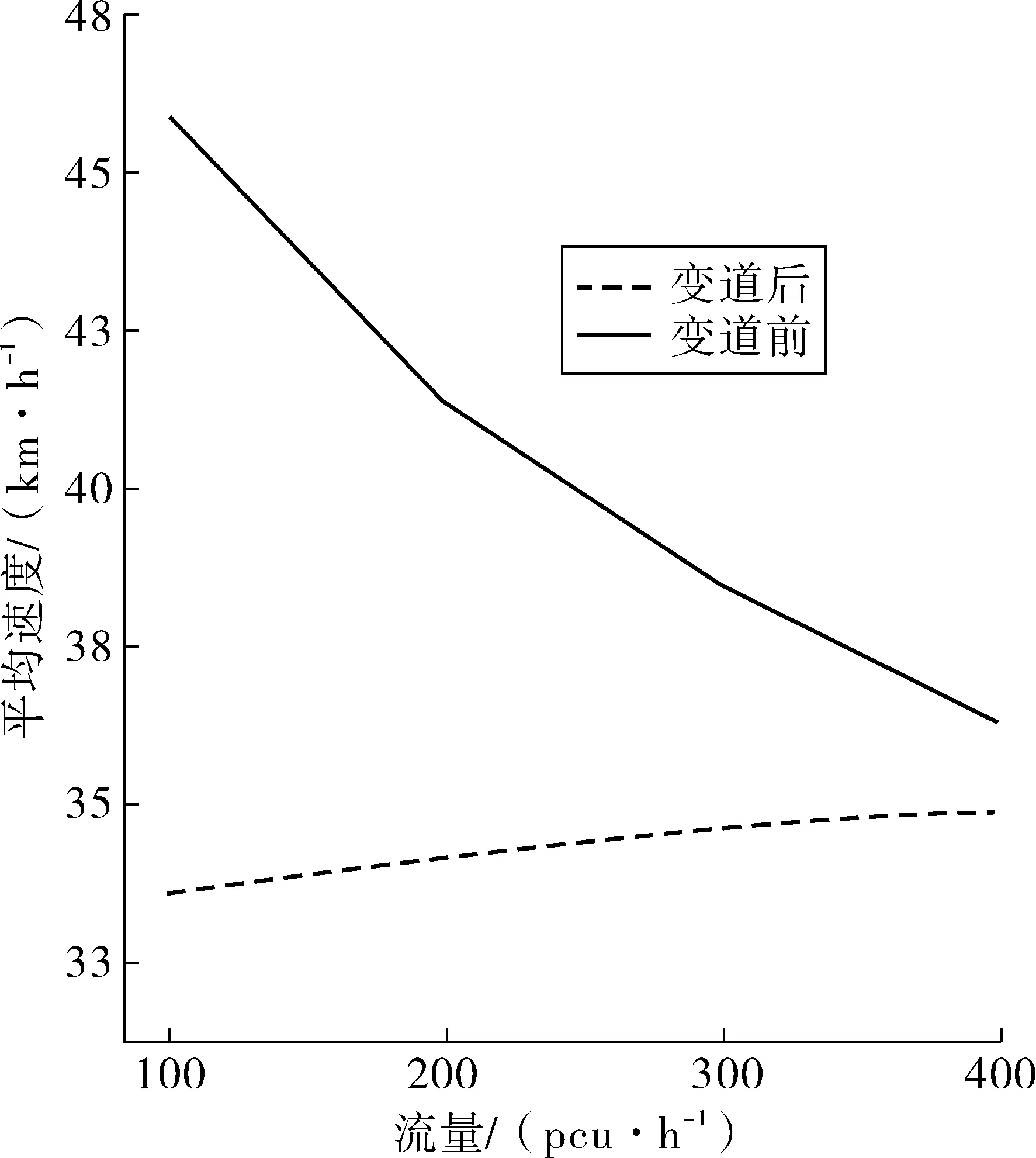
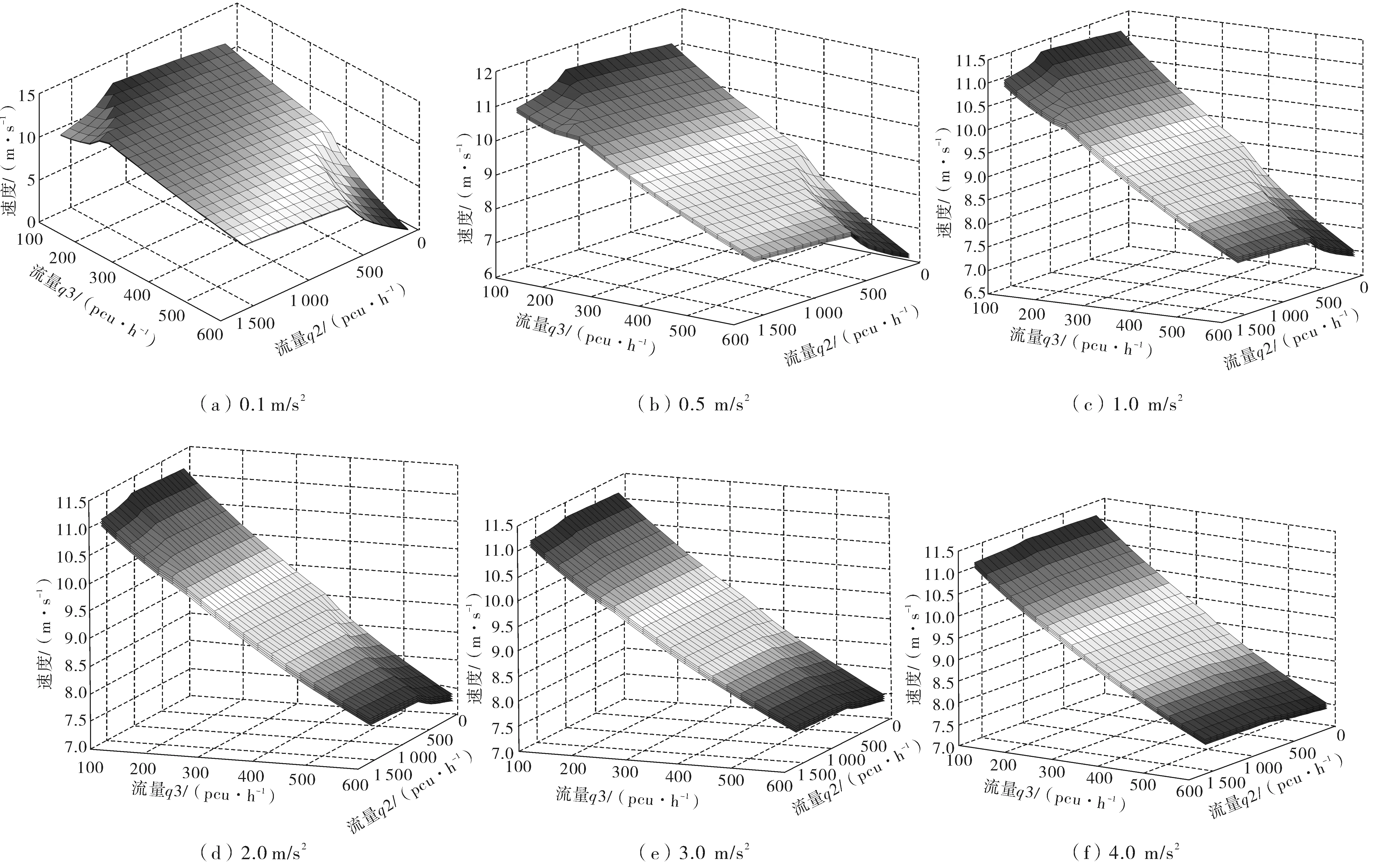
wOsinθ(t))]1/2}/aO 2aO(SAO(0)-wOsinθ(t))]1/2}/aO (14) 由于车辆正常换道θ在3°~5°之间,wO=1.5 m,因此满足:0.1 所以一般情形下,wOsinθ(t) {(vA-vO)-[(vA-vO)2+2aO(SAO(0)- wOsinθ(t))]1/2}/aO<0 (15) 当式(13)成立时有: 0 wOsinθ(t))]1/2}/aO (16) 2.1.2 变道车辆与目标车道后车的变道时间 此时的变道时间即为变道后能与后车保持最小安全距离的时间。图3为变道车辆O与A的运动轨迹,此时两车之间可能发生的碰撞形式有斜向碰撞和追尾碰撞。假设车辆变道开始的时刻为t0,变道结束后的时刻为t1,变道时间为ta,则ta=t1-t0。车辆在加速变道完成后,其速度与目标车道的车速保持一致,即vO(t)=vB(t)。则车辆的变道加速时间为: (17) 则在ta时间内变道车辆O行驶距离: (18) 在ta时间内目标车道后车B行驶距离: SB=vB.ta=vB(t1-t0) (19) 则变道车辆O与目标车道车辆B在变道后的纵向水平距离: (20) 变道车辆O能够不与目标车道车辆B发生碰撞,则必须S(t)>0,即: (21) 对于式(21),求解: t1,2={(vB-vO)±[(vB-vO)2+2aO(SBO(0)- wOsinθ(t))]1/2}/aO (22) 则式(22)的解为: ta>{(vB-vO)+[(vB-vO)2+2aO(SBO(0)- wOsinθ(t))]1/2}/aO (23) 或者: ta<{(vB-vO)-[(vB-vO)2+2aO(SBO(0)- wOsinθ(t))]1/2}/aO (24) 由于车辆正常变道在一般情形下,wOsinθ(t) {(vB-vO)-[(vB-vO)2+2aO(SBO(0)- wOsinθ(t))]1/2}/aO<0 (25) 所以此时的变道时间必须满足: ta>{(vB-vO)+[(vB-vO)2+2aO(SBO(0)- wOsinθ(t))]1/2}/aO (26) 由前文的分析可知,为了避免变道车辆与目标车道车辆产生碰撞,变道车辆与目标车道前车的变道时间: wOsinθ(t))]1/2}/aO (27) wOsinθ(t))]1/2}/aO (28) 当车辆从车道1变道至目标车道2时,若目标车道2后车距离变道车辆足够远时,则可以不考虑其影响,只需要满足目标车道2前车的最长变道时间;若目标车道2前车距离变道车辆足够远时,则可以不考虑其影响,只需要满足目标车道2后车的最短变道时间;若目标车道2前车与后车与变道车辆距离适中时,则需要考虑两者的影响。 根据实测数据分析,绝大多数变道车辆在变道时均优先考虑与目标车道前车的关系,因此笔者首先研究车辆变道满足目标车道前车要求的情形,此时: wOsinθ(t))]1/2}/aO (29) 如果要同时满足目标车道后车的要求,此时有: wOsinθ(t))]1/2}/aO (30) 假设目标车道的车辆行驶状态是一致的,即vB=vA,变道车辆均以相同的加速度aO进行变道,考虑不同的最小安全换道距离进行分析。 2.2.1 当SAO(0)=SBO(0) 2.2.2 当SAO(0)>SBO(0) 1)当满足: {(vB-vO)+[(vB-vO)2+2aO(SBO(0)- wOsinθ(t))]1/2}/aO 2aO(SAO(0)-wOsinθ(t))]1/2}/aO (31) 2)当满足: 0 wOsinθ(t))]1/2}/aO (32) 可以满足与目标车道前车A之间的安全变道要求,但是将对目标车道后车B形成影响,此时的影响时间为: 2aO(SBO(0)-wOsinθ(t))]1/2}/aO-ta (33) 式中: 0 wOsinθ(t))]1/2}/aO (34) 3)当满足: ta>{(vB-vO)+[(vB-vO)2+2aO(SAO(0)- wOsinθ(t))]1/2}/ao (35) 若满足与目标车道B之间的安全变道要求,但此时不能满足与前车的要求,即此时变道车辆将会与目标车道前车发生碰撞,因此不考虑此情形。 2.2.3 当SAO(0) 1)当满足: {(vB-vO)+[(vB-vO)2+2aO(SBO(0)- wOsinθ(t))]1/2}/aO 2aO(SAO(0)-wOsinθ(t))]1/2}/aO (36) 2)当满足: 0 wOsinθ(t))]1/2}/aO (37) 如果变道车辆与目标车道前车A存在变道间隙,变道车辆O欲变换到目标车道前车A,在此情形下要想变道成功,B车必须减速、跟驰或停车等待。因此,变道将对目标车道后车B造成影响,其影响时间为: 2aO(SBO(0)-wOsinθ(t))]1/2}/aO-ta (38) 式中: 0 wOsinθ(t))]1/2}/aO (39) 3)当满足: ta>{(vB-vO)+[(vB-vO)2+2aO(SBO(0)- wOsinθ(t))]1/2}/aO (40) 即变道车辆与目标车道后车B存在变道间隙,变道车辆O欲变换到目标车道后车B,此时变道车辆将不能满足目标车道前车的安全要求,即变道车辆将会与目标车道前车发生碰撞,因此不考虑对此情形。 综合上述内容,车辆变道对目标车道前后车的影响可以表述为: 2aO(SBO(0)-wOsinθ(t))]1/2}/aO-ta (41) 式中: (42) 相关研究[15]表明,变道车辆与目标车辆前车的最小安全距离: (43) 分析式(43)可知:SAO(0)的取值范围为[0,LA+wOsinθ(t)]。则变道车辆与目标车辆后车的最小安全距离为: (44) 分析式(44)可知:SBO(0)的取值范围为[LB+wOsinθ(t),+∞]。由于假设目标车道的车辆行驶状态是一致的,变道车辆与目标车道车辆为同一车型,即vB=vA,LA=LO,所以必然有SAO(0) 因此,当变道车辆与目标车道前后车存在变道间隙时,此时变道车辆对目标车道上游车辆的影响时间为: (45) 选择南京市中山南路为研究对象,采用摄像法获取道路交通相关数据。该道路为双向6车道的四幅路。为了便于统一研究,确定了车道编号规则,即最靠近主路中心线的车道为1,依次向非机动车道方向编号分别为2、3,如图4。 图4 中山南路各车道编号示意Fig. 4 Schematic diagram of numbering each lane ofZhongshan road 则存在:车道1→车道2、车道2→车道3、车道3→车道2、车道2→车道1等4种换道形式。经过实地调查发现,车辆从车道3变换到车道2的次数最多,如图5。 表1为4种情形下的换道时间对比分析。可以看出:换道类型为1-2的换道时间均值最小,换道类型为3-2的换道时间均值最大。换道类型为1-2时,换道时间的最大值为3.23 s,而换道类型为3-2时换道时间却为11.00 s。研究结果表明:当从车道1变换至车道2时,为自由变道,换道时间比较短;而从车道3变换至车道2时,由于变道条件不完全具备,车辆将实施强行换道,此时的换道时间较长。因此笔者重点研究车辆换道对车道2交通流的影响模型。 图5 各换道类型的换道次数Fig. 5 Number of lane-changing times for each lane-changing type 换道类型N极小值极大值均值标准差方差1-2260.650 03.230 01.755 0380.554 507 20.3072-1501.266 05.635 02.176 2000.821 726 60.6752-3741.038 07.529 02.424 6351.352 516 21.8293-21440.945 011.000 03.004 7361.349 460 41.821 以1分钟为观测时间间隔,以各车道为研究对象,获取交通流量与区间平均车速数据,建立了各车道的速度-流量模型,即: (46) 由于笔者假设变道是从速度低的车道向速度高的车道变换,且变道成功后无减速行为,因此S=0。当车辆从车道3变换到车道2时,变道车辆对目标车道2车辆的影响模型可以描述为: v=-2.031+0.842v2-0.04{[(v2-v3)+ (47) 将v2与v3的表达式代入式(47),得出最终的影响模型为: (48) 选取南京市中山南路为例,利用所建立的影响模型进一步分析各个影响变量对社会车辆速度影响的敏感性分析,进而解析车辆变道过程对社会车辆影响的分析机理。 相关研究表明[15],当变道车辆与目标车辆前车的速度差值越大时,其最小安全距离越小;当变道车辆与目标车辆后车的速度差值越大时,其最小安全距离越大;同时当变道加速度增大时,变道车辆与前车之间越不安全,而与后车之间越安全。 因此,车辆要成功换道到目标车道,其变道时间不仅与两车之间车速的差值有关系,还分别与变道时的加速度和换道车辆与目标车道前后车的最小安全距离密切相关。 由前文可知,式(16)为变道车辆与前车必满足的必要条件,其阈值为: {(vA-vO)+[(vA-vO)2+2aO(SAO(0)- wOsinθ(t))]1/2}/aO (49) 将式(16)代入,则式(49)阈值为: (50) 同样可以得出,变道车辆与后车的变道时间阈值为: (51) 从式(49)、式(51)可以看出,描述变道车辆与前后车变道时间的阈值与变道车辆与目标车道车辆的速度差与变道车辆的加速度有关。 为了能直观分析变道车辆与目标车道前后车之间的关系,假设变道车辆与目标车道的后车长度取值均为5 m,宽度取值均为2 m,车辆变道的平均角度θ=4°,选择不同的加速度对变道时间的阈值进行对比分析。图6为变道车辆与目标车道前车在不同加速度下的变道时间阈值。 图6 变道车辆与目标车道前车在不同加速度下的变道时间阈值Fig. 6 Lane-changing time threshold of the lane-change vehicle and the front vehicle on target lane at different accelerations 从图6可以看出: 1)变道时间的阈值与两车的速度差呈现单调递增的变化规律,即当速度差越大时,变道时间的阈值也越大。这说明当两车的速度差越大时,要完成变道所需的临界时间也越大;而当两者速度差越小时,则变道时间越小,说明在此情形下要完成变道,则所需的临界时间越小。 2)当变道车辆的加速度越大时,阈值越小。当变道车辆与目标车道速度差相同时,变道时间的阈值与加速度大小呈现反向的变化趋势,即加速度值越小,则变道时间的阈值越大,说明变道越不容易。 3)当变道车辆与目标前车符合变道条件时,若两者速度差较大,则变道车辆的加速度对变道过程有很重要的影响。 图7为变道车辆与目标车道后车在不同加速度下的变道时间阈值。 图7 变道车辆与目标车道后车在不同加速度下的变道时间阈值Fig. 7 Lane-changing time threshold of the lane-change vehicle and the rear vehicle on target lane at different accelerations 从图7可以看出:①变道时间阈值都与变道车辆与目标车道后车速度差值呈现单调递增的变化趋势;②变道时间阈值与加速度呈现单调递增规律,但当加速度在1.0~2.0 m/s2时,对阈值的变化影响很大,当加速度大于2.0 m/s2后,对阈值的影响较小。 图8为换道车辆以相同的加速度2 m/s2分别变道至目标车辆前车与目标后车,在不同的速度差时的变道时间阈值对比分析。 图8 换道车辆与目标车道前后车在不同速度差下的变道时间阈值Fig. 8 Lane-changing time threshold of the lane-change vehicle and the front and rear vehicle on target lane at different accelerations 从图8可以看出: 1)在相同的速度差下车辆进行变道时,以目标车道前车为变道对象所需要的时间比以目标车道后车为变道对象要短。 2)以目标车道后车为变道对象时,变道时间阈值-速度差的曲线变化的幅度要比以前车为对象要大,特别是当速度差≥6 km/h时,其变道时间增长的幅度非常明显。这说明变道车辆在满足与目标车道前后车最小安全距离的条件下,选择以前车为变道对象,所需要的时间更短,更能够有利于实现成功变道。 假设目标车道2流量为100~400 pcu/h,车道3的流量为500 pcu/h,车道3有车辆变道,此时由于变道引起车道2速度的变化值与无变道前的对比分析见图9。可以看出:变道引起了车道2车辆速度的下降,同时随着车道2流量的增大,变道前后的速度值变化幅度越来越小。这与实际情况比较吻合,说明模型具有一定的准确性。 图9 车道2变道前后速度对比分析Fig. 9 Comparison of velocity in lane 2 before and after lane change 图10为车道3的车辆变道至车道2时,车道2的车辆受变道影响后的速度。 图10 不同变道加速度下目标车道车流速度的变化Fig. 10 Variation of vehicle flow velocity in target lane at different transit accelerations 图10中加速度分别为0.1、0.5、1.0、2.0、3.0、4.0 m/s2,可以看出: 1)当变道车辆所在车道流量为500~600 pcu/h且目标车道流量为0~500 pcu/h时,或者当变道车辆所在车道流量为100~200 pcu/h且目标车道流量为1 000~1 500 pcu/h时,采取不同的加速度进行变道,对目标车道的车流速度影响较大。 2)当变道车辆的加速度越小时,由于变道引起的速度变化幅度越大,当变道加速度越大时,由于变道引起的速度变化幅度越小。 1)变道时间阈值与变道车辆与目标车道后车速度差值呈现单调递增的变化趋势,与目标车道后车加速度呈现单调递增的规律。变道车辆在满足与目标车道前后车最小安全距离的条件下,选择以前车为变道对象,所需要的时间更短,更能够有利于实现成功变道。 2)当变道车辆与目标车道前后车存在变道间隙时,此时变道车辆对目标车道上游车辆的可进行变道强制性变道满足的条件是若目标车道的平均车头时距小于总的变道时间阈值,但大于与前车的变道时间阈值,此时变道对目标车道交通产生影响。若目标车道的平均车头时距小于与前车的变道时间阈值,此时容易导致车辆追尾等交通冲突事件,则禁止变道。 3)当变道车辆所在车道的流量为500~600 pcu/h且目标车道流量为0~500 pcu/h时,或者当变道车辆所在车道的流量为100~300 pcu/h且目标车道流量为1 000~1 500 pcu/h时,车辆变道对目标车道车流速度的影响幅度较大。 4)当变道车辆的加速度越小时,由于变道引起的目标车道车流速度的变化幅度越大,反之,则越小。当变道车辆的加速度为0.1~2.0 m/s2时,对目标车道的车流速度影响较大。2.2 车辆变道影响时间
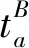
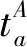
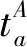
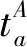
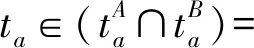
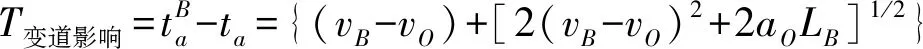
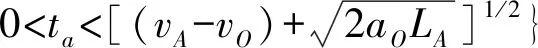
3 基于车辆变道影响的主路交通流模型
3.1 研究对象
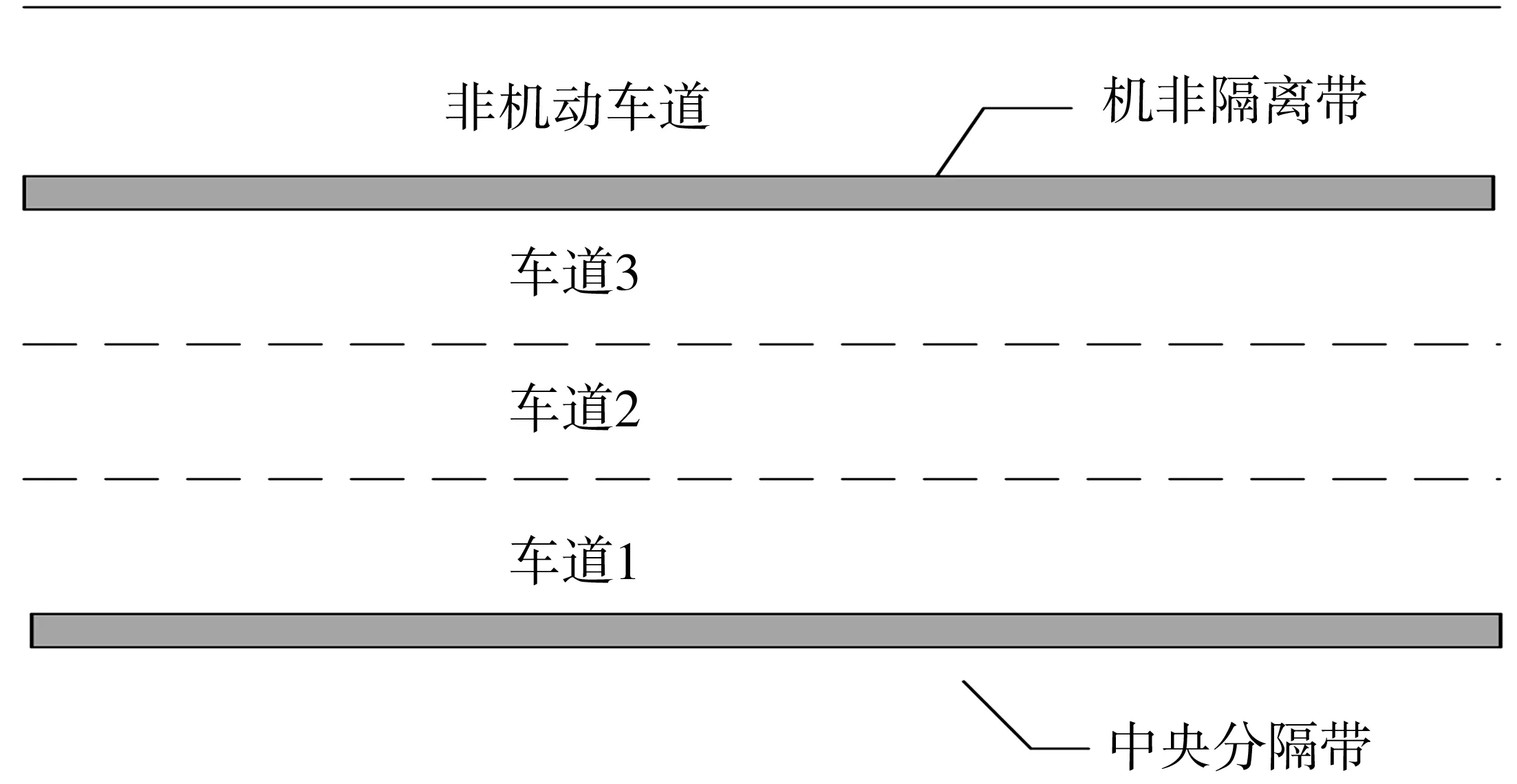
3.2 模型构建
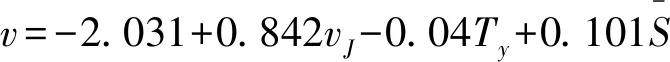
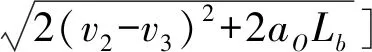
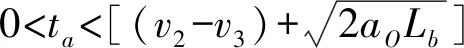
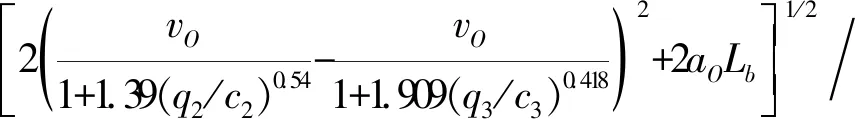
4 车辆变道对目标车道影响模型的敏 感性分析
4.1 变道时间阈值的特性分析
4.2 变道时间阈值的敏感性分析
4.3 变道前后速度分析
5 结 论

