基于非对称性GARCH模型的国债经济市场波动性分析

孙斐斐，施国洪

（1.江苏大学 管理学院，江苏 镇江212013；2.常州轻工职业技术学院，江苏 常州 213164）

0 引言

把握国债的波动性是投资者获利的基本要求。适度的波动性可以对经济市场产生积极的作用，它推动了金融产品的创新，发展了经济理论。通常采用国债收益率的标准差或方差来定量国债波动性，但是，经过多次研究发现，国债收益率不是呈现出简单的概率分布，而是随时间不断变化[1]。因此，为了准确地刻画出国债波动性，本文采用非对称效应的GARCH模型来模拟方差随时间变化特征具有明显的优势。

世界上对国债经济波动性研究有着较长的历史。Blank-scholoes提出了一种期权定价模型，这种模型假定了国债市场收益服从标准正态分布，即国债的波动率是不变的[2]。1976年，Morgan在研究中发现国债收益率的变化特征[3]，推翻了Blank-scholoes提出的模型[4]。1982年，Engle提出了ARCH模型，该模型基本可以模拟国债变化的时变性[5]。之后，Bollerslev在Engle研究的基础上补充了均方误差和条件方差两个参数，并命名为GARCH模型[6]。2010年，Sabiruzza-man在研究美国国债指数时采用了GARCH模型，验证发现，GARCH模型在非对称的形式下可以更好地反映国债市场的变化效应[7]。我国对国债市场收益率的波动性研究起步较晚，但是也不乏杰出的研究成果[8-10]。

为此，本文首先说明了非对称性GARCH模型的TARCH模型和EGARCH模型的表达式和参数情况，然后采用非对称性GARCH模型对我国国债经济市场的波动性进行分析。

1 非对称效应的GARCH模型

1.1 TARCH模型

TARCH模型可以很好地模拟出国债经济市场的非对称效应[11]。TARCH模型的条件方差公式如下：

其中，εt<0时，表示负面效应，dt=1，否则表示正面效应，dt=0。在TARCH模型中，正面效应和负面效应对条件方差的影响效果不同。正面效应会引入一个α的参数，负面效应则会增加一个α+γ的参数。如果γ>0则存在非对称效应，说明了非对称效应的效果造成了指数变化频率过快。如果γ≠0，表示指数是不对称的。如果γ<0，表示非对称效应的效果造成了指数变化频率过慢。

1.2 EGARCH模型

GARCH模型成立的条件是绝对值相等正面效应和负面效应影响因素引起的波动情况相同，即条件方差相同。GARCH模型的结果是绝对值相等正面效应和负面效应造成的指数波动收益情况相同且对称。但是，在现实的国债经济市场中，绝对值相等正面效应和负面效应影响因素引起的波动情况是不同的，国债指数下降幅度大于上升幅度。因此，采用GARCH模型描述国债指数的波动性并不可靠。而Nelson提出的EGARCH模型可以完成参数的非对称效应。基于EGARCH模型的条件方差公式如下：

其中，log()表示条件方差的自然对数，说明非对称效应是指数级变化的，同时条件方差也是非负值。如果纬<0的假设成立则表示非对称效应存在。

EGARCH模型的优势在于条件方差的数据是的自然对数形式，而肯定非负，也就不需要对条件方差公式进行其他限制来保证条件方差也是非负。

为了说明EGARCH模型的特性，这里介绍EGARCH模型的另一种表达式如下：

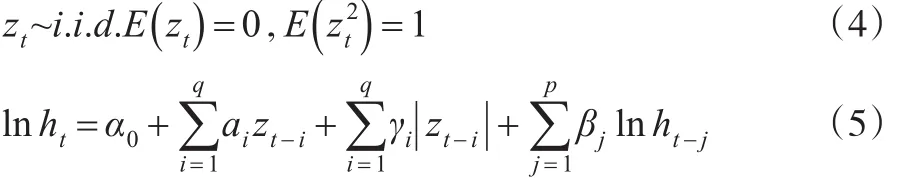
其中，et表示平均值模型的预估误差值，是实际值的时间序列。令ψt为截止到某一时刻t的所有指数数据集合，ht表示指定指数数据集合ψt-1时et的条件方差。公式（5）则为EGARCH模型的条件方差计算表达式。

为了简化计算，令ft=lnht，则EGARCH模型的条件方差化简为：

而在条件下，EGARCH模型具有高稳定性，同时具有唯一的严格稳定遍历性。

为了计算EGARCH模型的参数，本文采用极大似然估计法进行计算。设有n+q个稳定样本序列e1-q，e2-q，…，e-1，e0，e1，…，en。集合ψt为截止到某一时刻t的所有指数数据集合。由公式（5）可知，et关于ψt-1的条件密度为：

其中，θ为参数向量。e1，…，en是对于ψ0的联合条件密度为公式（8）：

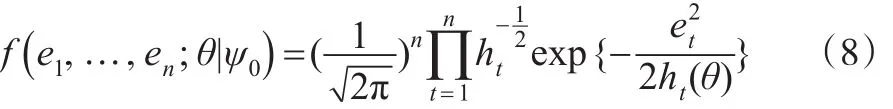
自然对数条件似然函数如下：

关于θ的一阶和二阶偏导数，结果如下：

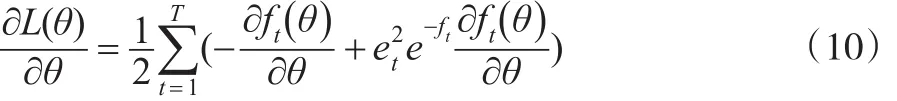
化简为：

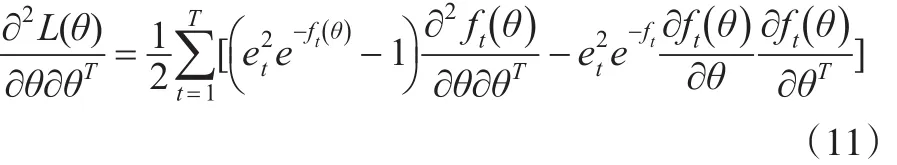
对应于参数θ的矩阵为：

且满足公式（13）：

此时可以取迭代估计参数θ：

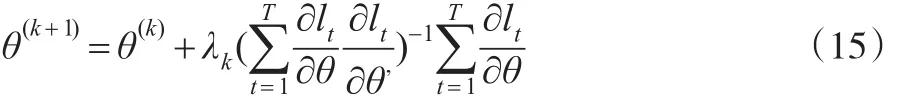
其中，λk为第k步步长，lt为自然对数似然函数，为最优解方向向量。不断迭代，直到条件不满足。

2 国债经济增益的波动性实证分析

结合对非对称效应的GARCH模型的描述，本文将采用GARCH模型对我国国债经济增益的波动性进行分析。

2.1 数据说明

本文以上海交易所的2010年10月30日至2016年4月20日期间每个交易日国债收盘指数为样本数据，共计1332组原始数据，数据源于新浪财经国债频道[12]。在整个国债交易市场中，上海证券交易所（以下简称上证）的国债交易量占到了全国总量的99%。与股票价格波动类似，国债价格波动通常采用国债指数（LEB）[13]反映。国债指数早在2003年对外发布，国债指数是以上证交易所上市的全部固有利率的国债为样本，根据国债发行量来增加利率，每月最后一个交易日剔除年限不足一年的国债。上证国债指数是上证指数系列中最为重要的指数之一，上证国债指数能够体现我国债券市场的整体波动情况，是我国国债价格的“显示器”。为了定量分析我国国债市场的波动性，本文使用上证国债指数来衡量国债市场的波动性。

2.2 统计性描述

图1是上海证券交易所国债指数波动示意图。从图中可以看出，国债指数变化造成的债券收益率变化表现出明显的时变性、聚簇性和并发性。

图1 上证国债指数波动图

图2（见下页）是上海证券交易所国债指数描述性统计图。从图中可以发现，样本内的债券指数收益率为0.04%，标准差为2.13%，偏差为-0.405，左偏差峰值为4.929，其值远大于正态分布的峰值3，收益率表现出明显的峰高底厚的特点。Jarque-Bera计算值为242.707，收益率在最小显著水平情况下不同于标准正态分布。因此，如果样本数据采用F检验或者基于正态分布检验方法均无法检验收益率。

图2 上证国债指数描述性统计图

2.3 国债指数收益率序列的平稳性检验

从图2可以看出，上证国债指数收益率以均值为中心上下波动，收益率指数不趋向于某一值。因此，本文使用ADF平稳性检验手段对国债指数收益率序列进行检验。选择滞后4阶，并带截距无趋势项参数，ADF平稳性检验结果如表1所示。

表1 上证国债指数收益率ADF平稳性检验结果

从表1的ADF检验结果来看，1%显著性水平检验条件下MacKinnon的Prob.*值为-3.6588，5%显著性水平检验条件下MacKinnon的Prob.*值为-2.3420，10%显著性水平检验条件下MacKinnon的Prob.*值为-2.9463。t检验数据为-15.93460，小于相应的临界值，因此拒绝H0，表示上证国债指数收益率数据服从I（0）过程，不存在单位根，是平稳数据。

2.4 GARCH模型实证

采用非对称效应TARCH模型对上证国债指数收益率的波动性进行研究。TARCH模型的模拟结果如表2所示。

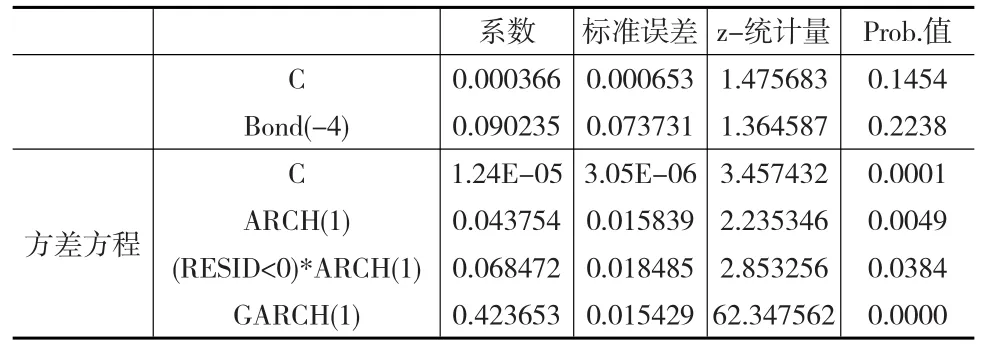
表2 TARCH模型模拟结果

TARCH模型中，非对称性效应是由表2中的(RESID<0)*ARCH(1)结果描述的，公式（17）中项的系数为0.06847，值大于0，表示显著性为正，说明TARCH模型存在非对称性效应，同时也能说明上证国债指数收益率的波动性存在非对称性效应，负面效应引起的波动比正面效应引起的波动大得多。正面效应出现时，即εt>0，那么有一个伪=0.073731的冲击；负面效应出现时，即εt<0，那么有一个α+γ=0.073731+0.068472=0.142203的冲击。

采用非对称效应EGARCH模型，对上证国债指数收益率的波动性进行研究。EGARCH模型的模拟结果如表3所示。

表3 EGARCH模型模拟结果

EGARCH模型中同样存在非对称性效应，负面效应引起的波动比正面效应引起的波动大得多。EGARCH模型的A=0.145474，非对称项纬的系数显著性小于0，其值为-0.035474，说明上证国债指数收益率的波动性存在非对称性效应。正面效应出现时，即εt>0，那么有一个α+γ=0.145474+(-0.035474)=0.11的冲击；负面效应出现时，即εt<0，那么有一个α+γ=0.145474+(-0.035474)×(-1)=0.180948的冲击。

2.5 实证结论

根据对上证国债指数收益率的波动性进行实证分析，得出以下结论：

（1）GARCH模型可以很好地解释我国债券市场收益率的波动性现象。虽然GARCH模型已经被发达国家所采纳，但是该模型不影响在我国债券市场的应用。经过本文研究发现，上证国债指数收益率的波动性的条件方差特性较为显著，这样也同样可以证明本文采用的GARCH模型能够实际反映上证国债指数收益率的波动性的变化规律，而且准确性较高。

（2）从时间角度上来看，上证国债指数收益率的波动性体现出了较强的可变性和波动集簇性。波动集簇性是上证国债指数的主要影响因素。收益率不具有自相关性，但是收益率的平方具有较强的相关性，这种相关性并不表现出一种正态分布，而是呈现出一种峰高底厚的特点。

（3）通过构建TARCH模型和EGARCH模型，上证国债指数收益率表现出较强的非对称性效应。同等强度的负面效应对上证国债指数收益率的冲击力要远远大于同等强度的正面效应对上证国债指数收益率的冲击力，负面效应造成的上证国债指数收益率的波动性更加剧烈。

3 对策和建议

为了构建完善的债券市场，市场波动性的存在十分必要，因为适度的市场波动性可以较好地刺激金融市场。通过实证分析发现，我国的债券市场还存在一定的问题，对此，本文提出以下意见和对策：

（1）完善信息公示体制。我国债券市场的波动聚簇性现象较为普遍，市场中的大部分国债交易不够合理，影响债券价格的稳定性。信息公示效率低下使得债券价值的资源配置能力下降。信息公示制度可以保证债券市场基本信息的充分公开，能够充分发挥金融市场作用，优化信息传递机制，减少不必要的非理性投资。

（2）强化理性交易观念。如今，债券交易所中的广大群众缺乏一种理性的交易观念，偏执于某一种债券投资，缺少一定的债券交易知识和投资理财能力。因此，可以加强对债券投资理财的教育力度，使得金融市场交易更加稳定合理。

（3）优化政府债券市场的管理。政府不需要过度干预债券市场秩序。当债券市场泡沫化程度较高或者债券市场不景气时，政府的直接干预会破坏金融市场的供求关系，严重扰动市场的波动性。因此，政府作为行政职能部门需要明确其基本工作，建设公平公开的债券交易体系，稳定债券市场秩序，尽量减少对市场的过多干预。

（4）增强风险管理力度。债券市场存在着比股票市场更高的金融风险，提高风险管理力度更具必要性。同时，为了保障投资者的投资权益，也需要提高风险管理力度，加强风险管理制度建设，避免过多的市场动荡。

（5）加强债券市场的法制建设。当前，我国债券市场的法律法规准则还不够完善，部分投资者会进行违法违纪行为，扰乱市场秩序，破坏市场的资源配置能力。因此需要大力推进债券市场法制化建设，规范交易行为。

4 总结

本文采用非对称效应的GARCH模型来准确模拟国债指数收益率的波动情况。基于国内外现有的成果，首先介绍了非对称效应的GARCH模型中的TARCH模型和EGARCH模型，这两种模型是描述国债市场非对称效应的两个经典模型。然后采用GARCH模型对我国国债经济增益的波动性进行分析，样本数据为上海交易所的国债指数数据，并结合上证国债指数的波动图和描述性统计图进行数据分析。接着采用ADF平稳性检验方法对国债指数收益率序列进行检验，检验结果发现上证国债指数收益率数据服从I（0）过程，不存在单位根，是平稳数据。使用TARCH模型和EGARCH模型分别对国债指数收益率的波动性进行实证分析，实证结果发现TARCH模型和EGARCH模型均存在非对称性效应，且同等强度的负面效应对上证国债指数收益率的冲击力要远远大于同等强度的正面效应对上证国债指数收益率的冲击力，负面效应造成的上证国债指数收益率的波动性更加剧烈。