动态粒子群优化K-means的图像分割算法研究

杨雨航

（重庆师范大学计算机与信息科学学院，重庆401331）

0 引言

图像分割是一个从目标图像中具有独特性质的区域中将感兴趣的目标提取出来的一门技术或者一个过程，对于后续进行的图像分析和图像识别有着不可忽视的影响，是完成图像处理的关键步骤[1]。目前，图像分割已经广泛应用于包括工业、医学、交通、农业等各个领域[2-3]。

K-means聚类算法是一种半监督学习方法，特点是能够快速处理大数据集，目前已经在图像分割领域得到广泛应用[4]。但K-means聚类算法存在以下几点局限性[5]：K-means聚类算法采取随机选取初始聚类中心的办法，因此，聚类结果对聚类中心的依赖较高；K-means聚类算法需在算法进行初始化时即确定聚类数目；K-means聚类算法的结果受噪声点影响较大，对噪声较为敏感，容易被少量数据影响最终聚类结果；K-means聚类算法容易收敛至局部最优解，从而错过全局最优解。

为了克服这些局限性，粒子群优化算法（Particle Swarm Optimization，PSO）因其拥有强大的全局搜索优化的能力这一特点[6]，带给国内外一些研究人员启发，提出了一些通过结合PSO粒子群优化算法对K-means聚类算法进行改进的方法。如穆瑞辉提出的基于粒子群优化的模糊K-means目标分类算法[7]；班俊硕提出的基于PSO与K-means聚类的混合算法[8]；刘桂红等提出的利用PSO+K-means混合算法来改进全局优化能力[9]。然而，粒子群优化算法PSO本身也存在一些局限性[10]，由于标准粒子群优化算法的惯性系数为初始化时的一个固定值，该值的选取如果不合适，可能会出现粒子在某局部极端之间徘徊，导致算法结果收敛至局部最优解甚至难以收敛至一个结果。

本文通过结合改进的粒子群优化和K-means聚类算法来进行图像分割。首先采用双边滤波对目标图像进行平滑降噪处理，以减轻噪声对后续图像分割过程中K-means算法聚类结果的影响，再通过动态调整PSO粒子群优化算法中的惯性系数的大小更新每次迭代中的粒子速度，使其能够克服易于陷入局部最优的缺点，获得较好的图像分割效果。

1 相关理论

1.1 K-means算法

K-means算法应用于图像分割[11]时，即将目标数字图像划分为K个簇，通常情况下，K-means算法将每一幅目标图像都抽象成具有n维向量的数据点集合X={X1,X2,…,Xn}，找出该集合的子集 Z={C1,C2,…,Ck}来最小化目标函数：

式中，‖Xj-Ci‖2表示目标图像数据点Xj到聚类中心Ci的欧氏距离，D越小，说明聚类效果越好。因此，K-means算法通过对目标函数进行多次迭代使其达到最小化，并在每次迭代时不断更新聚类中心，更新公式为：

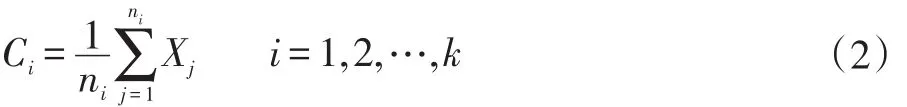
式中，ni表示第i个簇中数据点的个数，聚类中心在更新过程中，同一聚类中心的簇中的数据点相似度朝着增大的趋势发展，而不同簇之间数据点之间的相似度逐渐减小的方向发展，直至聚类中心不再变化，说明已达到收敛，聚类完成。

1.2 标准粒子群算法

粒子群算法[12]，也叫做粒子群优化算法或者鸟群觅食算法，算法初始化时先随机化问题最优解，经过不断迭代计算，最终得到最优解。对于每一个优化问题，PSO都将该问题的解看作是搜索空间中忽略体积和质量的粒子，每一个粒子都有其对应的初始位置和初始速度，并随着适应度值的不同每一次迭代都有相应变化，每个粒子都有一个对应的适应度，该适应度的大小由目标优化函数决定。假定在D维空间中存在N个粒子，粒子i的位置表示为Xi={Xi1,Xi2,…,XiD}，粒子i的速度表示为Vi={Vi1,Vi2,…,ViD}，粒子i其个体经历的最好位置表示为pbesti={pi1,pi2,…,piD}，粒子群经历的全局最佳位置表示为gbest={g1,g2,…,gD}。

第k次迭代粒子i的第j维的速度更新计算公式如下：

第k次迭代粒子i的第j维位置更新计算公式如下：

式中，w为惯性系数,；c1和c2为加速度常数，也称学习因子，分别代表着粒子的自我学习能力和集体学习能力，取值区间为[0,4]，通常取 c1=c2=2；r1和 r2为两个在区间[0,1]均匀分布的随机数。

2 改进的动态PSO优化K-means的图像分割算法

2.1 平滑滤波

由于图像在采集、获取、传送和转换过程中的环境复杂多变，例如会受到光照、电磁等因素影响，均存在不同程度的被可见或不可见的噪声干扰，导致图像不仅在视觉质量上有所下降，噪声甚至可能会掩盖某些重要图像细节[13]。因此，在对采集到目标图像做进一步的分割处理时，可先对图像进行必要的滤波降噪[14]处理。

本文算法选择双边滤波来完成对目标图像的降噪处理。双边滤波[15]是一种非线性滤波方法，通过将目标图像的像素值相似度与空间邻近度相结合完成采样，以达到同时考虑到灰度相似性和空域信息的目的，从而在完成对图像进行降噪的同时对图像边缘也能够进行很好保存。滤波效果如图1所示。

图1 平滑滤波结果对比

2.2 动态惯性系数

根据前文对标准粒子群算法的描述可知，该算法容易错过全局最优解，而陷入局部最优解的徘徊。因此，将固定惯性系数进行动态调整是一个解决该问题的有效途径。本文算法使每次迭代的惯性系数w服从一个概率分布，其概率密度函数为：

2.3 动态PSO优化K-means算法

本文算法在完成平滑滤波预处理之后，剩下的工作主要分为两个阶段：第一个阶段为利用动态粒子群优化算法搜索全局最优解得到初始聚类中心；第二阶段为K-means算法继续进行迭代直至收敛。首先从将目标图像平滑滤波处理后得到的具有n维向量数据点集合X中随机选取m个数据点构成优化问题的解空间，也即后续在K-means算法阶段用来初始化聚类中心；然后将集合X中剩余数据点分配给这m类，令xi为集合X中的第i个数据点，cj为第j个聚类中心，若||xi-cj||=min||xi-ck||（其中k=1,2,…,m），则将数据点xi归入第j类，该粒子的适应度计算公式为：

由此，动态粒子群算法的收敛程度可由粒子的适应度变化表示，即当粒子适应度不再变化时，算法收敛。本文选择使用方差δ2来表示适应度变化，当方差小于某一指定值时，认为该算法达到全局最优，其计算公式如下：

式中，favg表示粒子的平均适应度，计算公式如下：

当动态粒子群优化算法达到全局最优后，将输出的最优解结果作为第二阶段K-means聚类算法的初始聚类中心，从而在一定程度上克服K-means聚类算法初始聚类中心的随机选取对聚类结果影响较大这一局限性，有效提高K-means算法的收敛速度。

本文算法流程如下：

Step1.读取目标图像数据，采用双边滤波进行降噪处理；

Step2.计算每个粒子适应度；

Step3.更新惯性系数，粒子速度和位置；

Step4.计算适应度方差；

Step5.判断方差大小，若大于规定值，则返回Step2，若不大于规定值，则输出结果到下一步骤；

Step6.将输出的全局最优解作为聚类算法的初始聚类中心；

Step7.计算数据点到聚类中心距离；

Step8.更新聚类中心直至收敛，若聚类中心不再变化，输出结果，否则，返回Step7。

3 实验结果及分析

3.1 实验环境及实验数据

本文所提算法的实现平台为Anaconda3-5.2.0-Windows-x86_64，实验所用计算机硬件配置为：Intel Core i5-4200U CPU@1.60GHz，内存：4.00GB（3.75GB可用）。为了证明本文算法的分割性能，与K-means算法和标准粒子群优化K-means的PSOK算法进行图像分割对比实验。本文算法实验参数设置如下：

（1）在三个算法中K-means算法部分，令初始聚类中心数量为k=3；

（2）在 PSOK 算法中，令 c1=c2=2.0，w=0.8；

（3）在本文算法中，令c1=c2=2.0。

三种不同算法图像分割结果如图3所示，后文将从定性分析和定量分析两个方面进行图像分割效果研究分析。

3.2 定性分析

观察图2可知，相较于K-means算法和PSOK算法，在以图像中的动物为目标进行分割时本文算法在保留细节的基础上可以获得更优的图像分割效果，在相同区域轮廓完整，边缘清晰，总体分割效果更令人满意。因此，本文算法分割性能要优于K-means算法和PSOK算法。

图2 三种不同算法图像分割效果图

3.3 定量分析

本文算法在图像分割上性能优于标准粒子群优化K-means的PSOK算法的原因，除了本文算法引入了双边滤波对目标图像进行降噪预处理之外，最主要的原因是本文算法对惯性系数进行动态调整之后，粒子群优化算法的全局优化性能大大提升。本文选取了Sphere函数和Griewank函数两种标准测试函数对本文使用的粒子群优化算法和标准粒子群优化算法进行比较。参数设置如表1所示。

表1 标准测试函数参数设置

使用上述两种标准函数对本文算法使用的粒子群优化算法与标准粒子群优化算法的迭代结果如图3所示。

图3 标准测试函数迭代过程

图3中，DPSO代表本文改进的动态粒子群优化算法，PSO代表传统标准粒子群优化算法。从图3（a）中可以看出，对于Sphere函数，两种算法均能非常快速地收敛至最优解，差异非常小，但本文改进的动态粒子群优化算法仍然更快速的收敛至最优解。从图3（b）中可以看出，对于Griewank函数，虽然两种算法最后均收敛至全局最优解，然而标准粒子群优化算法在中途有陷入局部最优解的趋势，明显动态粒子群优化算法更快更稳定。因而，采用本文动态粒子群优化算法在图像分割中实现了预期效果。

4 结语

本文提出了一种改进的结合动态粒子群优化与K-means聚类的混合算法来进行图像分割，该算法通过引入双边滤波在最大限度保留边缘信息的情况下对图像进行降噪预处理，再通过动态调整惯性系数达到提高粒子群算法优化能力的目的，从而使该算法在图像分割整体上获得优异的效果。实验结果表明，本文算法结合了K-means算法快速收敛的特点和PSO全局搜索的能力，且相对于标准粒子群优化K-means的PSOK算法获得更好的分割效果和更高的分割效率。但是，对于PSO算法中惯性系数的动态调整只是随机产生，自适应程度不足，在后续研究中将继续对惯性系数和学习因子的动态调整进行自适应的改进，使其更好的分割图像。