钢板爬壁机器人三角架组合体结构优化设计
曾红 魏旭东 冯帆


摘要:三角架组合体作为履带式爬壁机器人的重要支撑件,其机械性能决定船体大面积焊接作业的可靠性。以钢板吸附力为基础,对爬壁焊接机器人三角架组合体进行有限元分析,得到模型的受力、变形和前四阶模态振型;随后分析求解相关结果,利用参数灵敏度分析方法,对三角架组合体的结构进行优化。运用ANSYS Workbench软件对优化后的结构进行模拟仿真,得到总组合体的变形量、应力值均有一定程度下降,模态振型的表现形式转变为较平稳的平动或摆动状态。提高了机器人运动的平稳性,对大面积船体焊接质量的稳定性提供技术支撑。
关键词:
机器人三角架组合体;有限元分析;灵敏度分析法
DOI:10.15938/j.jhust.2019.01.004
中图分类号: TP242 2
文献标志码: A
文章编号: 1007-2683(2019)01-0023-06
Structural Optimization Design of Tripod Assembly of Steel Plate Climbing Robot
ZENG Hong 1,WEI Xu dong 2,FENG Fan 3
(1 Rongcheng Campus,Harbin University of Science and Technology,Rongcheng 264300,China;
2 School of Mechanical and Power Engineering,Harbin University of Science and Technology,Harbin 150080,China;
3 College of Mechanical and Electronic Engineering, China University of Petroleum,Qingdao 266580,China)
Abstract:As an important supporting part of the crawler wall climbing robot, the mechanical properties of the tripod assembly determine the reliability of the large area welding operation of the hull In this paper, based on the adsorption force of steel plate, finite element analysis is performed on the tripod assembly of the wall climbing welding robot to obtain the force, deformation and the first four modes of the model Then we analyze and solve the relevant results, and the structure of the tripod assembly is optimized by the method of parameter sensitivity analysis Using ANSYS Workbench software to simulate the optimized structure, the deformation and stress values of the total assembly are reduced to a certain degree, and the form of modal shape changed to a more stable translational or swing state Optimized combination improves the smoothness of the robot′s movement and provides technical support for the stability of large area hull welding quality
Keywords:robot triangular plate combination; finite element analysis; parameter sensitivity analysis
0引言
在机器人领域中,最引人注目的新技术之一就是行走式或爬行式智能机器人。其中爬壁机器人技术日渐成熟,逐渐运用于高层写字楼玻璃幕墙维护或清洗、重型船舶大型设备检测与焊接,尤其是履带式机器人[1]。其稳定性好、适应能力强,对提升劳动生产率、更好地符合企业现有生产条件、降低生产中安全事故的发生有重要意义[2-4]。
关于爬壁机器人的研究,国外已有半个世纪的历史,特别是欧美和日本的研究所[5]。国内研究人员也在爬壁机器人理论知识及实验优化做了许多的研究工作,如文[6-8]。但研究方面多为机器人的建模仿真和验证, 無法为爬壁机器人的优化提供理论依据。
随着有限元分析的日益发展,其在土木建筑、流体力学、磁场中运用十分广泛,工厂和企业通过有限元技术可以进行模拟仿真、优化产品结构和减少设计成本等[9]。因此,在力学分析的基础上,本文利用有限元分析方法对爬壁机器人中对实际焊接作业有重要影响的三角架组合体进行分析,得到相应的应力、变形参数与前四阶模态振型。通过图表分析数据、比较强度极限,从而提早发现重要部件三角架结构在实际运作条件下出现的问题。随后根据实际作业中的技术和功能要求,结合参数灵敏度分析方法,对三角架组合体的结构进行优化,使组合体充分保证爬壁机器人进行焊接作业时的安全可靠。
1爬壁机器人的力学分析
要实现机器人在壁面的作业,就要进行力学分析,以便于后续在携带焊接设备等负重的情况下进行讨论。当爬壁机器人运动时,要提供足够的吸附力,防止机器人在爬行过程中出现大角度偏斜、脱落等事故。
本文采用的爬壁機器人为履带式,其底座结构如图1所示。
这里以机器人最主要的运动形式,沿壁面匀速为例进行分析。机器人如果上爬,驱动力由两侧电机提供。根据相关资料文[10],结合静力学中的几个危险状态,焊接爬壁机器人沿船舶壁面做直线运动时的力和力矩平衡方程见式(1)、(2)所示。
∑ n1 i=1 F f-G-ma=0(1)
W2(∑ n2 i=1 N i)+GH+maH-W2F p=0(2)
式中m为机器人总质量;i为机器人从动轮编号(i=5~12);N i 为电机驱动力(i=1,2),a为机器人的运动加速度。H为本机器人重心G到地面高度,W为两个驱动轮间距。
整理后,我们得到匀速运动时,机器人的吸附力满足的条件如式(3)所示:
F p≥ max G+maμ,2HW(G+ma) (3)
设计 H 为160.mm, W 为385.mm,爬行速度 v 不超过0 1.m/min,并且可以变速调整;焊枪等负载加机器人自重 G '为40.kg,最大重力加速度 a 为0 15.g。取摩擦因数 μ 为0 5,根据上述数据,带入公式(3)中,计算后得机器人的临界吸附力为 1.440 N。
2机器人三角架组合体的有限元仿真
2.1机器人三角架组合体静力分析
由于三角架与轮轴和机器人侧板轴相连接,其构成的组合体的强度对复杂工况下焊接工作的安全与稳定有重要影响。因此,利用ANSYS Workbench对履带式焊接机器人的三角架组合体进行分析具有较强的工程应用价值。
首先在软件中设定三角架组合体的金属材料为304不锈钢,泊松比 ρ =0 3,弹性模量 E =200.GPa,密度 μ = 7.890 kg/m 3。随后利用Mechanical模块对模型结构进行处理。从动轮采用自动划分网格,轴及三角架采用四面体网格划分方法。设置模型的边界约束为三根轴的轴端,顶轴设置为完全约束,其余轴设置为无摩擦约束。采用第1章的数据进行分析,在每个轮子施加180.N的力,随后加载自身重力,求解得到的三角架组合体变形与应力结果如图2、图3所示。
当三角架组合体在只受自身重力时,如图3所示,最大应力为26 477.MPa,出现在邻近顶轴下端的三角架上。根据相关资料[11],可知室温下不锈钢的屈服极限大于该应力值;不锈钢的最大变形量为 0 002.8 mm,各部件也均出现一定的应力和应变,故应将结构进一步优化,提高三角架的承载能力。
2.2机器人三角架组合体模态仿真
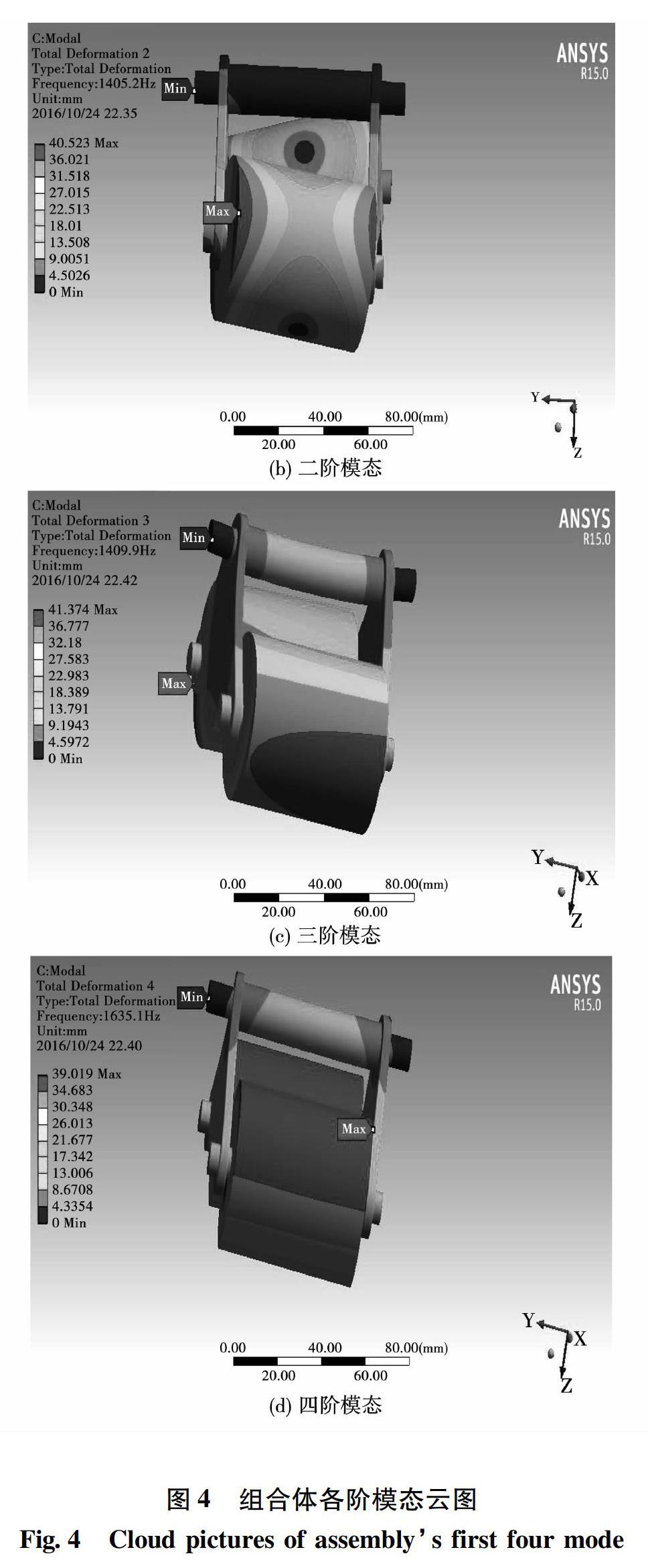
模态是机械结构的固有振动特性。通过该分析,可评价现有结构系统的动态特性、诊断故障及放止共振等。将模态模块与先前处理的静态模块相关联,生成三角架组合体的前四阶模型固有频率和振型效果云图如图4所示。
由于三角架整体结构的刚度主要由第一阶固有频率所决定,故对低阶系统进行研究即可发现模型运动时存在的问题。由图可知,一、三阶振型变形主要出现在两从动轮处下部;四阶振型变形主要出现在两从动轮处上部。特别需要关注的是二阶变形,其变形出现在轮子两侧面且扭转方向不同,变形量在40.mm左右,轮子或与三角架发生碰撞。当电机或磁铁振动频率与其发生共振时,三角架易产生较大变形,使机器人的运动发生偏斜,使焊接质量变差甚至造成一定的生产事故,这也进一步说明了三角架进行优化设计,降低三角架组合体的共振变形或扭转。
3实验验证
将单个三角架作为实验验证模型,进一步验证模态仿真的准确性,如图5所示。三角架的几何参数与有限元分析中相同,如表1所示。通过力锤冲击实验来获得工件应变模态,采用Kistler5236B旋转式测力仪和5238B电荷放大器收集实验过程信号。分别用PCB 3330B加速度计和测量了16个激励点位置的加速度响应和动态应变响应。采用灵敏度为10 42.mv/g的PCB加速度传感器,东华DH5922采集系统收集加工过程加速度信号。采用灵敏度为3 41.pC/N力锤来进行模态试验获得三角架的固有频率。采用激光位移传感器测量加工过程工件的变形量。激光位移传感器型号为KEYENCE LK H020,采样周期为5.μs。应变模态测量装置示意图如图5所示。
图6为敲击点设置示意图,给出了16个不同力锤敲击点的位置。然而,在实验中,存在一些不可避免的误差因素,可能导致在结构边界附近的应变测量不准确。因此,在实验结果中去除了在边界处点1和点16的不准确的实验应变数据。试验所得三角架四种应变模态如图7所示。
从表1和图7可以看出,初始动态有限元模型和三角架结构的动态特性几乎相近。初始动态有限元模型计算频率与相应测量结果之间的最大相对误差为14 40%,最小相对误差仅为1 87%。因此,动态有限元模型可用于进行相关的模态分析。
4机器人三角架的优化设计
鉴于上述分析,综合考虑爬壁机器人从动轮的可靠性及在船舶等墙壁环境的要求,可利用参数的灵敏度分析对三角架进行优化设计。
4.1优化尺寸的选择
ANSYS Workbench的Design Exploration模块就是利用灵敏度分析原理进行参数优化的。其原理是通过数学和机械理论分析,选择对机械结构特性影响较大的设计参数,根据灵敏度数值大小,確定影响较大的参数,随机进行优化[12]。
针对三角架组合体的结构,初步选取如图8所示的5个尺寸。这些尺寸都处于应力较大区,且尺寸不存在干涉或依赖关系,不会导致模型再生失败,可进行尺寸优化。
在不影响组合体整体性能的前提下,确定优化尺寸初始值及变化范围如表2所示。需要注意的是,D3、D4和D5均为对称分布,即若要进行优化时,各相应尺寸均需要进行调整。
基于六西格玛的判定原则,通过Ansys自身迭代,5个尺寸对三角架的应力和一阶固有频率灵敏度影响情况如图9所示。
4.2优化尺寸灵敏度分析
图9显示灵敏度出现正负值,当值为正,说明当此尺寸增大时,目标函数的值会相应增大;值为负,说明尺寸减少时,目标函数的值会相应减小。分析后发现D3、D4和D5对三角架组合体的影响较大,因此选择这些尺寸进行最终优化。
ANSYS Workbench的DOE环节可探究灵敏度最大时各尺寸出现的概率,优化后的尺寸分别为:D3 11 2.mm,D4 66 7.mm和D5 6 3.mm,圆整得D3 11.mm,D4 67.mm和D5 6.mm。随后按照本文第2章的设计步骤进行分析,得到改进后组合体的静力学仿真结果和模态分析结果见表3所示。
由表格数据可知,三角架优化后,使得总组合体变形量继续减小;最大应力值下降17%。低阶模态有了一定的提升,避开了振动频率较低的电机或液压系统;同时二阶模态振型转为平动,变形量明显减少;其余各模态振型多为较平稳的平动或摆动,避免了不安全的工况发生。
5结论
三角架组合体对爬壁机器人的焊接作业稳定性有重要影响,因此本文提出了一种关于机器人三角架及其组合体运行稳定性的理论计算方法、有限元分析和优化设计方法。将理论分析的计算结果带入ANSYS Workbench中进行有限元及模态分析,结果表明三角架变形量和等效应力均小于许用值,其结构设计基本满足设计要求。针对三角架组合体的模态振型可能导致机器人出现偏移、失稳等不安全现象发生,本文采用参数灵敏度分析的方法对模型进行优化,优化后三角架组合体的变形量、应力值均有一定程度下降,模态振型多转变为平动或摆动,说明优化后的组合体令机器人运行更加平稳,使爬壁机器人充分按照指定命令行进,充分保证了实际焊接作业的安全可靠,对机器人其他部件的优化设计具有一定的参考价值。
参 考 文 献:
[1]SCHMIDT D,BERNS K.Climbing Robots for Maintenance and Inspections of Vertical Structures A Survey of Design Aspects and Technologies[J]. Robotics and Autonomous Systems,2003(61):1288.
[2]YBERLE J.Application of Climbing Robot Rosy Ⅱ in the Business of Building Conservation[J].Iaarc, 1998: 111.
[3]吴明晖.面向焊接任务的轮足式非接触磁吸附爬壁机器人的研究[D].上海:上海交通大学,2014:6.
[4]李志梅,付宜利,王树国.四轮驱动滑动吸盘爬壁机器人的动力学研究[J].机器人,2010,9(32):601.
[5]SCHMIDT D C,HILENBRAND K, et al.Omnidirectional Locomotion and Traction Control of the Wheel driven Wall climbing Robot CROMSCI[J].Robotica,2011,29:991.
[6]衣正尧, 弓永军,等. 新型除锈爬壁机器人附壁建模与仿真[J]. 四川大学学报,2011,43(3):211.
[7]孙玲,王祖温. 船舶除锈机器人转向运动学分析[J]. 机械设计与制造,2014, 7(7):189.
[8]仝建刚,马培荪,陈俊梅. 履带式磁吸附爬壁机器人壁面适应能力的研究[J]. 上海交通大学学报,1999,33(7):851.
[9]梁君,赵登峰. 模态分析方法综述[J]. 现代制造工程,2006(8):139.
[10]KRZYSZTOF T, ROBOT M.Instantaneous Kinematics and Dexterity of Mobile Manipulators[C]// Proceeding of IEEE International Conference on Robotics and Automation,2000:2493.
[11]濮良贵,陈国定. 机械设计(第九版)[M]. 北京:高等教育出版社,2013.
[12]刘超峰,张功学. DVG850高速立式加工中心主轴箱灵敏度分析[J]. 组合机床与自动化加工技术,2010(5):88.

