径向通风电机流体流动及传热特性分析
丁树业 夏之慧 李海玲 仵程程 隋宇
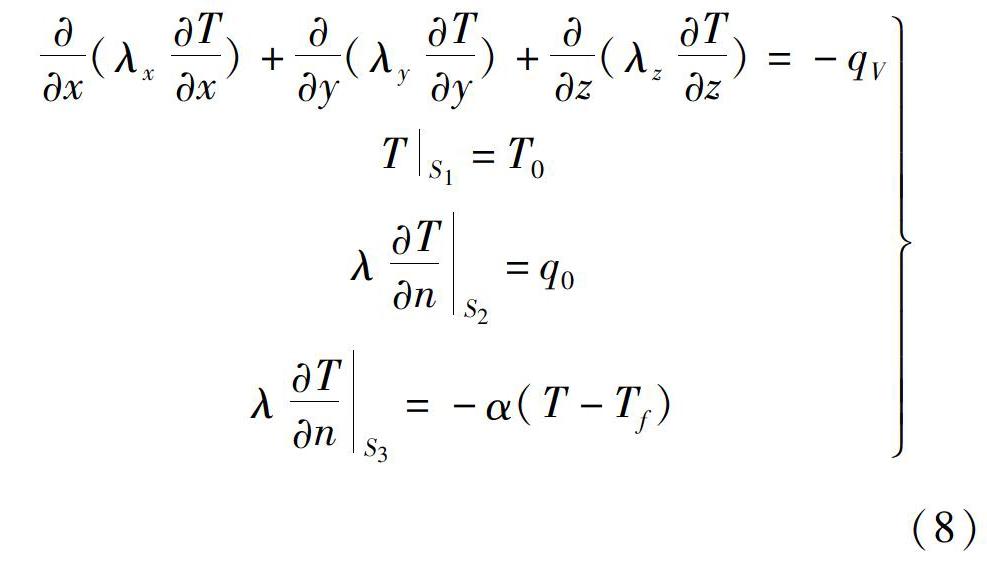
摘要:为研究径向通风电机内部流体分布、传热性能及温升特性,根据径向通风电机通风结构及传热特点,建立三维流动及传热耦合的物理模型和数学模型,结合工程实际给出基本假设和边界条件,采用有限体积法对流体场及温度场进行求解,得出电机内部冷却介质流动性能、传热特性及电机各部件的温升分布情况。最后,对电机定转子股线、绝缘及铁心温升分布做了详细分析,获得电机温升分布趋势及温升最大值的位置。为径向通风电机综合物理场的准确计算以及通风结构的优化提供了理论依据。
关键词:
径向通风电机;流体流动;传热特性;耦合
DOI:10 15938/j jhust 2019 01 006
中图分类号: TM315
文献标志码: A
文章编号: 1007-2683(2019)01-0034-07
Analysis of Fluid Flow and Heat Transfer Characteristics for Radial Ventilation Generator
DING Shu ye,XIA Zhi hui,LI Hai ling,WU Cheng cheng,SUI Yu
(School of Electrical and Electronic Engineering, Harbin University of Science and Technology,Harbin,150080,China)
Abstract:In order to study distribution of fluid flow, the characteristic of heat transfer,and temperature rise characteristics of radial ventilation generator,a mathematical and physical model of 3D fluid flow and heat transfer coupled was established according to structure characteristic of radial ventilation generator Flow fluid and field was calculated coupled using finite volume method by giving fundamental assumptions and corresponding boundary conditions From the research,the performance of fluid flow characteristic of heat transfer,and temperature rise distribution of generator were obtained Finally,the temperature rise distribution of the strand, insulation and iron core of stator and rotor are analyzed respectively, the maximum temperature rise position of each parts of the motor are obtained The theory gist for accurate calculation of synthetic physical fields and structure optimization for the radial ventilation generator is provided
Keywords:radial ventilated generator; fluid flow; heat transfer characteristics; coupling
0前言
隨着电机单机容量的增加,势必增加电机尺寸、结构的复杂性以及电机内电磁负荷的强度,即大大增加了电机研究的难度。电机电磁负荷增加,电机内各部件温度随之升高,而电机温升分布作为衡量电机运行状态的重要指标之一,在电机的综合性能评价中占据重要的指导地位[1-3]。因此,对电机的温升计算及通风结构优化尤为重要。
目前国内外专家对电机流-热耦合场计算方面的研究,通常以一个槽为研究对象,且假设冷却气体垂直进入径向通风沟,但事实并非如此。本文从流-热耦合角度采用有限体积法对径向通风电机进行全面透彻的研究,不仅可以弥补电机温度场传统计算方法的缺陷,而且提高径向通风电机数值计算的精度,该求解方法充分考虑电机内部各种因素的影响,使仿真过程更加贴近实际运行环境,具有重要的理论意义及工程实际价值。
本文根据径向通风电机通风结构及传热特点,建立三维流动及传热耦合的物理模型和数学模型,结合工程实际给出基本假设和边界条件,采用有限体积法对流体场及温度场进行仿真计算,并对电机的流体流动性能及各重要部件的温升分布进行详细分析,获得电机温升分布趋势及温升最大值的位置,为径向通风电机综合物理场的准确计算以及通风结构的优化提供了理论依据。
1模型的建立
1 1计算流体动力学控制方程
电机中的流体在运动过程中必须满足三大守恒方程,其三大守恒方程式如下所示[4-5]:
质量守恒方程:
ux+vy+wz=0(1)
式中:u、v、w分别为x、y和z方向的速度分量。
动量守恒方程:
(ρuu)x+(ρuv)y+(ρuw)z=
xμux+yμuy+zμuz-px(2)
(ρvu)x+(ρvv)y+(ρvw)z=
xμvx+yμvy+zμvz-py(3)
(ρwu)x+(ρwv)y+(ρww)z=
xμwx+yμwy+zμwz-pz(4)
式中:ρ为流体密度;μ为动力粘度;p为流体压力。
能量守恒方程:
(ρuT)x+(ρvT)y+(ρwT)z=
xλ lc pTx+yλ lc pTy+zλ lc pTz(5)
式中:c p為流体比热容;T为温度;λ l为流体的导热系数。
在电机内部流体流热问题的求解变量都可以用通用形式的的控制方程进行表示,通用方程如下所示[6]:
通用控制方程式为:
t(ρφ)+div(ρuφ)=div(Γgradφ)+S(6)
其展开形式为:
t(ρφ)+x(ρuφ)+y(ρvφ)+z(ρwφ)=
x(τφx)+y(τφy)+z(τφz)+S(7)
式中:可以代表u、v、w、T等求解变量;φ为通用变量;S为广义源项;Γ为广义扩散系数。
1 2数值传热学控制方程
本文只对电机稳态运行时温度场进行数值计算,因此可以将导热方程中时间项去掉,在本文中电机铁心导热系数呈现各向异性。因此,根据上面的假设,电机内温度场计算中三维导热控制方程在笛卡尔坐标下可以表示为如下形式[7-9]:
x(λ xTx)+y(λ yTy)+z(λ zTz)=-q V
T S 1 =T 0
λTn S 2 =q 0
λTn S 3 =-α(T-T f)(8)
式中:T为初始温度(℃);λ x、λ y、λ z分别为不同材料沿x、y、z轴的导热系数( W/(m 2·K) );α为表面散热系数( W/(m 2·K) );q V电机内的总热源值( W/m 3 );T 0为边界面处的温度值;T f为电机的环境温度(℃);S 1为恒温边界;在数值计算之前,必须给出q 0的值,其数值大小为边界面S 2上热源密度。
1 3通风结构
本文径向通风电机采用密闭式通风冷却系统,电机上部冷却器流出的冷却气体进入电机的端部气腔,当转子旋转时转子风沟内槽钢等效为离心式风扇,使电机内部产生压力差,促使冷却气体由电机两端进入电机内部,由于冷却气体与电机部件充分接触产生对流换热,最后从转子径向通风道流出电机本体从而带走电机热量,经出风口流回冷却器完成一次密闭循环流动。
2电机求解模型的建立
2 1基本假设
径向通风电机结构较复杂,为了合理的简化求解,做如下假设[10-14]:
1)只对电机稳定状态时的流体场进行计算,因此导热方程不含有时间项;
2)电机内部冷却气体的雷诺数很大(Re>2300),故采用湍流模型进行求解;
3)电机内部冷却气体流速远小于声速,即马赫数(Ma数)很小,故冷却气体为不可压缩流体;
4)电机定、转子端部股线采用直线段等效处理;
5)对定、转子股线绝缘、层间绝缘以及主绝缘等效为一个绝缘体;
6)电机各部分浸漆均匀,绝缘良好;
7)定、转子上下层股线施加热源相同,忽略其集肤效应。
2 2流体场求解域及边界条件
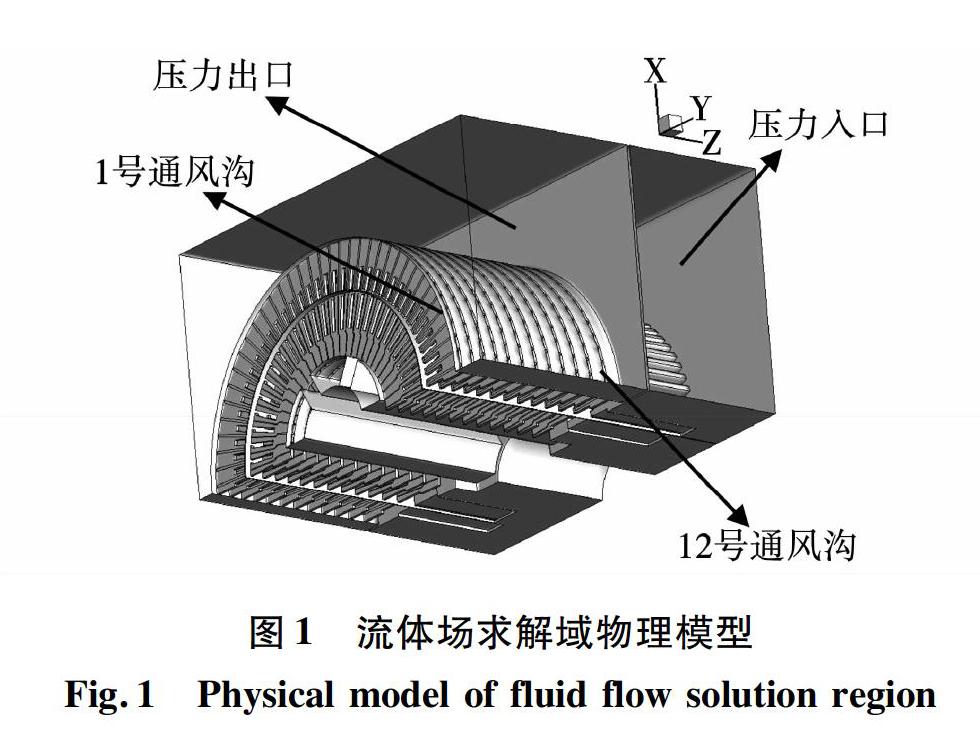
根据该径向通风电机轴向及周向均对称的特点,在基本假设的基础上,取电机轴向及周向均1/2区域作为流体场求解域物理模型,即整机的1/4为研究对象。其物理模型如图1所示。
电机流体场计算边界条件设置如下[13]:
1)以一个标准大气压为初值,入口为压力入口边界,出口为压力出口边界;
2)轴向对称面设置成对称边界条件,周向对称面设置成周期边界条件,其余的边界面均设置成无滑移边界。
2 3温度场求解域及边界条件
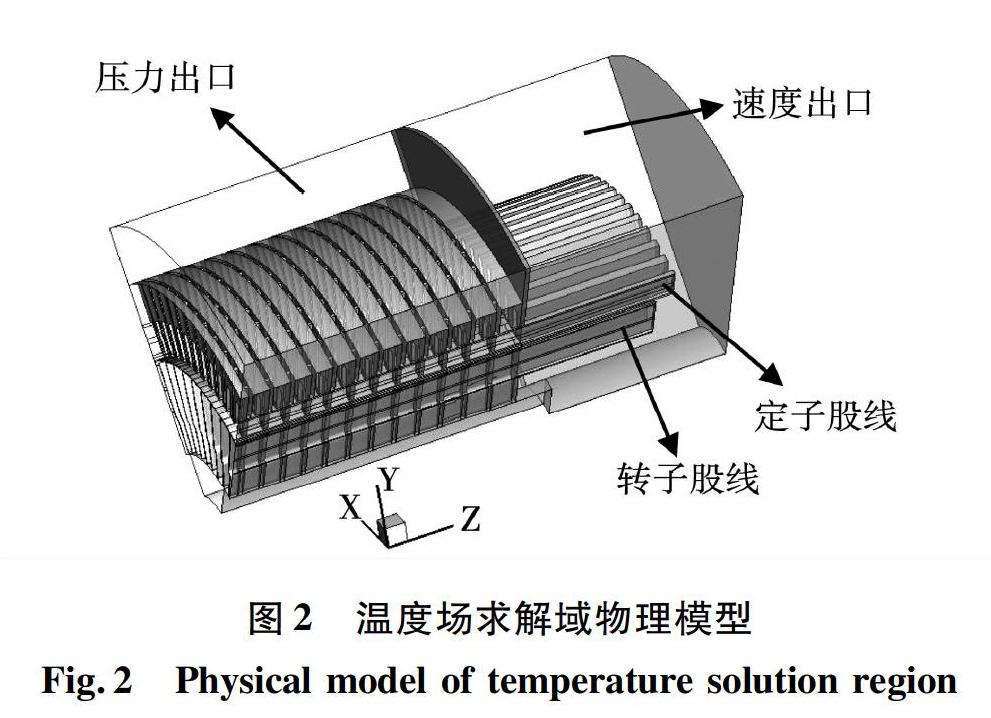
由于该电机在轴向及周向完全对称,在基本假设的基础上,为了降低电机温度场计算难度,又不降低计算的准确性,取电机轴向1/2、周向1/6区域作为电机求解域物理模型,即周向取12个定子槽,9个转子槽作为研究对象,电机的求解域物理模型如图2所示。
根据电机流体场计算结果,采用流-热耦合数值方法对电机温度场进行数值计算,电机温度场计算边界条件设置如下[15]:
1)电机空气入口设置成速度入口边界条件,速度值为0 52.m/s;
2)电机空气出口设置成压力出口边界条件,压力初始值为一个标准大气压;
3)电机轴中心端面为对称边界条件,其它边界均为绝热面;
4)转子区域流体与电机额定转速相同,均设置为 1.200 rpm。
2 4电机热源的分析
电机在额定运行时电机将产生损耗,即电机电磁损耗、机械损耗以及杂散损耗。表1给出了电机各部分损耗。
根据电机在额定状态下损耗大小,对电机定转子铁心及绕组施加热流密度,进而对电机进行温度场求解。
3流体场计算结果分析
3 1整体流体场计算分析
径向通风电机内流体场计算结果如图3所示。
从总体流体迹线分布可以看出,冷却气体在入风口附近流速较低,到气腔后速度逐渐升高,且靠近电机顶部的冷却气体流速相对于电机底部数值较大,并且电机定子部分较转子部分变化更加明显。这是由于转子以恒定转速旋转,定子在空间位置上与机壳保持相对静止,电机顶部和底部相对位置对转子影响较小,但是对定子影响较大,导致端部气腔内定转子部分流体流速分布不一致。冷却气体由端部气腔沿轴向风道进入电机内部,且转子径向风沟内流体流速较高。冷却气体经气隙进入定子径向风道,流速降低,且冷却气体在定子区域流速明显降低,流线分布较稀疏,这是由于冷却气体在定子径向风沟内受到沿程阻力的影响,且定子风道出现回流,使冷却气体在径向风道内发生碰撞,能量损失严重。
3 2整域内流体场流量计算结果分析
通过仿真计算,电机由转子旋转而产生的内部冷却气体的总风量为4 941.m 3/s,理论计算时,电机所需冷却风量为 4 078.8 m 3/s,因此,可以初步判断,单独采用转子自力扇风性能的冷却系统可以满足电机的通风要求。为了分析电机内部冷却气体分布规律,提取电机转子区域、定转子气隙及定子区域内流量分配数据以及各部分在总流量中所占百分比,如下表2所示。
从表2中可以看出,冷却器流出的冷却气体经入风口进入电机端部气腔,冷却定转子端部绕组后经转子支架气腔几乎全部进入定转子区域,流量损失较小。一方面,是由于转子构件起到离心风扇的驱动作用,另一方面,是由于该电机采用定转子风道沿轴向对齐布置,利于电机内部冷却气体的流通。
3 3径向通风沟内流速分析
为详细分析径向通风沟内的流体流变特性,取流量最大的径向风沟为研究对象,图4给出了1号通风沟中心截面速度分布云图。
从图4中可以看出转子区域流体速度远远大于定子区域。随着径向长度的增加转子流体速度逐渐增大,在气隙处达到最大。定子通风槽钢迎风面与背风面流体流速差异更加顯著,即定子通风槽钢迎风面流体流速大于背风面,但是在径向方向流体速度变化平缓。这是因为风从电机顶部入口进入电机端部气腔,分配给电机的各个径向通风沟,由于电机转子旋转而产生离心力作用从而使转子区域内风速不断升高,在转子风道出口与气隙的接触处风速达到最大值,而定子区域受入风口流速及转子旋转影响较小,沿径向方向变化不明显。
4温度场计算结果及传热特性分析
4 1电机整体温升特性分析
经过完整的数学描述和物理模型的建立,再结合电机各部分材料的物理属性,施加热流密度及边界条件后进行温度场计算,电机的温升分布云图如图5所示,计算结果如图6所示。
由图5可知,电机定子区域温升较高,而电机端部及转子区域温升相对较低。这是由于进入电机内的冷却气体首先冷却电机端部,然后经转子支架气腔进入转子径向风沟,冷却转子铁心及绕组,此时转子区域温度降低而冷却气体因吸收转子热量使自身温度升高,冷却气体再经气隙进入定子径向风沟后冷却定子的能力减小,使定子温升偏高。
通过计算结果图6可以得出以下几个结论。
1)电机各部分温升各不相同,总体上定子温升均高于转子;
2)定子区域,股线温升最高,为93.K,转子区域,温升最高处位于转子股线处,为77 6.K;
3)转子区域各部分平均温升、最高温升及最低温升呈现相同的变化趋势,即转子股线温升最高,绝缘温升次之,铁心温升最低。
4 2电机定子温升分析
定子铁心温升分布云图如图7所示。
由图7可知,定子铁心区域整体温升变化不大,即铁心两端温升低,中间温升高,铁心区域最高温升出现在靠近端部的9~11号径向风沟附近,达83 6.K。受端部气腔冷却空气影响,到铁心端部位置温升又明显降低。
从图8、图9中可知,随着轴向长度的增加,定子股线温升呈现先增大后减小的趋势,最大值位于靠近端部的中间位置,温升值为93.K。整体而言,靠近电机中间位置定子上下层股线温升几乎相同,但是越靠近电机端部位置,下层绕组温升下降幅度越明显,这是由于冷却空气刚进入端部气腔时,首先吹拂定子下层股线,冷却性能好,冷却气体进入径向通风沟后虽然首先冷却上层股线,但是定子通风沟内空间狭小,加上此时冷却气体温度较高,对上层股线及下层股线冷却能力偏差不大。
图10为定子绝缘温升分布云图,从图中可知,定子绝缘温升变化趋势与定子股线变化趋势基本相同,但是定子绝缘温升略低于定子股线温升值,其最大温升值为91 2.K。
综上可知,电机定子区域温升最大位置位于定子股线,绝缘温升次之,铁心温升最低。由于该电机采用F级绝缘水平,因此在电机额定运行时绝缘水平满足要求。
4 3电机转子温升分析
图11为转子铁心温升分布图,从图中可知,冷却气体冷却转子铁心的能力最佳,温升最低,铁心部分最高温升为68 1.K,最低温升为21 3.K。
图12为转子绝缘温升分布云图,从图中可知,转子绝缘最高温升为77 2.K,其最高温升与转子股线温升值相差不大,但是转子绝缘最低温升较低,最低值为29 2.K。
综上可图13为转子股线沿轴向长度温升分布图,从图中可知,与定子区域相比,转子股线平均温升明显降低,最高温升达77 6.K。随着轴向长度的增加,转子股线温升先增加然后减小。但是,转子下层股线温升明显低于上层股线温升值,这是因为端部气腔及径向风沟内冷却气体均首先冷却转子下层股线,冷却效果好。
综上可知,电机转子区域温升最大位置位于转子股线,绝缘温升次之,铁心温升最低,这是由于该径向通风电機通风特点所致。
5结论
本文以全封闭循环冷却系统的径向通风电机为研究对象,对电机三维流体场及温度场进行了数值仿真分析。从流-热耦合角度采用有限体积法对径向通风电机进行了全面的分析,获得如下结论:
1)电机内部冷却气体的总风量达4 941.m 3/s,高于电机所需冷却风量;因此,单独采用转子自力扇风性能的冷却系统可以满足电机的通风要求;
2)随着径向长度的增加,风沟内流体流速呈非线性变化,在气隙处达到最大,其速度值为74 67.m/s;冷却气体进入定子径向风沟,回流现象明显,流体流速降低;
3)端部气腔冷却气体经轴向风道进入定转子径向通风沟,流量损失较小;在轴向方向上,电机中部的风沟流量最大,越靠近端部的风沟流量越小;
4)定子平均温升较高,转子平均温升较低;绕组温升最高,绝缘温升次之,铁心温升最低;电机最高温升点位于定子股线,数值为93.K;在F级绝缘等级下,该径向通风电机满足绝缘要求。
参 考 文 献:
[1]黄东洙.大中型异步电动机电磁场与温度场数值计算[D].哈尔滨理工大学,2004.
[2]王水发,陈德为.基于ANSYS的异步电动机电磁场分析[J].电气开关,2011,2:20.
[3]杜海,曲延滨,张鹏.新型旋转电磁热机流体流动与传热的耦合计算与实验[J].电工技术学报,2015,12:291.
[4]王福军.计算流体动力学分析[M].北京:北京清华大学出版社,2004:1,119,31.
[5]陶文铨.数值传热学[M].西安:西安交通大学出版社,2001,(5):1,347,137,567.
[6]周俊杰,徐国权,张华俊.Fluent工程技术与实例分析[M].北京:中国水利水电出版社,2013:14.
[7]WIGGERT P.Mechanics of Fluids[M].北京:机械工业出版社,2003:136.
[8]赵镇南.传热学[M].北京:高等教育出版社,2008:1.
[9]LI XR,CU G.Coupled Electromagnetic and Thermal Analysis of Stator Insulating Structure[C]// ICEMS 2003:146.
[10]曹君慈,李伟力,程树康,等.复合笼条转子感应电机温度场计算及相关性分析[J].中国电机工程学报,2008,28(30):96.
[11]LIU Y J,LEE Y,JUNG H K,et al.3D Thermal Stress Analysis of the Rotor of an Induction Motor[J].IEEE Transactions on Magnetic 2000,36(4-1):1394.
[12]XYPTERAS J,HATZIATHANASSIOU V.Thermal Analysis of an Electrical Machine Taking into Account the Iron Losses and the Deep bar Effect[J].IEEE Transaction on Energy Conversion 1999,14(4):996.
[13]孙兆琼.基于流-热协同机理的永磁风力发电机结构优化[D].哈尔滨:哈尔滨理工大学,2012:6.
[14]李伟力,李守法,谢颖,等.感应电动机定转子全域温度场数值计算及相关因素敏感性分析[J].中国电机工程学报,2007,24:85.
[15]丁树业,王海涛,郭保成,等.50kW永磁同步电机内流体流动特性数值研究[J].电机与控制学报,2014,9:30.

