基于ABAQUS的Lamb波椭圆法探伤的仿真分析

王高平，魏 鸣，石 政，徐 博

(武汉工程大学 机电工程学院，湖北 武汉 430205)

0 引言

随着我国工业化进程的高速发展，工业化产品及其设备已普遍应用于社会的各行各业，而这些产品的结构离不开板状结构。板状结构在加工成型的过程中会产生缺陷，为避免发生设备故障和安全事故，及时发现板件缺陷和分析缺陷很重要[1]。

兰姆(Lamb)波在检测薄板结构时不会出现扩散衰减，与金属薄板的中性面相比，Lamb波传播时会出现频散现象而形成多种模态，其速度依赖于频率和厚度之积(频厚积)[2]。随着波的频率和板件厚度的改变，其模态也随之改变，所以，在研究Lamb波的传播特性时，Lamb波的频散曲线很重要。利用MATLAB编程求解Lamb波波动方程，得到其频散曲线，来确定频厚积与模态间的关系，为仿真奠定基础[3]。

本文基于椭圆定位法则[4]，运用ABAQUS软件对Lamb波在铝板中的传播过程进行仿真。分别建立健康、缺陷铝板模型并进行网格划分，计算时间步长和增量步长，加载中心频率为250 kHz的汉宁窗调制波，分别得到健康、缺陷铝板的x-y图和差信号图,并进行分析和计算，从而确定损伤的具体位置[5]。

1 Lamb波的频散特性

Lamb波被广泛应用于结构健康监测中，它是一种在厚度与激励声波波长为相同数量的声波导中、由纵波和横波相互耦合而成的一种弹性波，在薄板中有对称和反对称两种传播形式。频散特性是主动Lamb波在薄板中传播的主要特性之一，它主要描述了频厚积改变时Lamb波的相速度(群速度)的变化趋势。在自由边界条件下，各向同性材料薄板的Lamb波表面波的频散方程[6]为

(1)

(2)

(3)

cp=ω/k

(4)

(5)

d=h/2

(6)

式中：k=ω/cp为Lamb波波数，ω=2πf为Lamb波的角频率，f为Lamb波的频率；h为薄板厚度；cT，cL分别为Lamb波横波和纵波波速；cp，cg分别为Lamb波的相速度和群速度[7]。

根据式(1)～(6)求出铝板中cT=3 090 m/s、纵波波速cL=6 390 m/s[8]。式(1)中，幂次取+1与-1，分别表示Lamb波对称和反对称模态方程，利用图解法和二分法，用cL、cT、cp将整个区间分为4个，分别对对称和反对称模态方程进行求解，借助MATLAB的编程和绘图功能求解方程,且绘制出群速度和相速度的频散曲线，如图1、2所示。

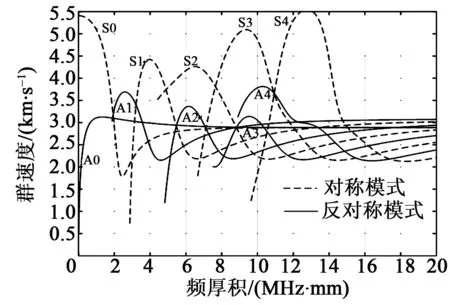
图1 Lamb波群速度频散曲线图

图2 Lamb波相速度频散曲线图

由图1、2可看出，任意一个频厚积至少对应2种或以上的模态，随着频厚积的增加，模态的形式越复杂，这也是Lamb波在薄板中的频散现象，由于多模态对后期数据处理制造很大的障碍，为了便于分析，尽量只激发单模态下的Lamb波，即频厚积选择1 MHz·mm。

2 Lamb波激励信号的参数选择与加载方式

本次研究采用窄带激励的方式产生Lamb波激励信号。通常采用加窗函数对正弦信号进行截取的方式来获取Lamb波的窄带信号，这里选取加载汉宁窗进行激励,Lamb波激励信号[9]为

(7)

式中：fc为激励波形的中心频率;t为激励波形传播时间;n为正弦波周期数目。

由图1可知，随着频厚积的逐渐增大，Lamb波发生频散现象，且每个模态的速度都不同，这样会使后期的信号处理复杂化。在Lamb信号处理的应用中，通常只激发Lamb波的S0和A0模态来进行分析，即频厚积选择1 MHz·mm来激发单一模态的Lamb波。综上所述，选择中心频率250 kHz、周期数目5、幅值10 V的Lamb波作为激励信号。将式(7)展开可得

(8)

由式(8)可看出，Lamb波是由3个正弦函数叠加而成，在设置载荷时需加载3个正弦周期函数。图3为激励信号时域图。

图3 Lamb波激励信号时域图

3 椭圆法定位薄板损伤的仿真分析

本次研究以椭圆法定位为基础实现损伤识别[10]。对损伤的板件进行检测时，如果损伤位置不在检测路径上，那么观测点B会收到两部分信号，一部分是从激励点A直接传入，另一部分是经损伤信号反射而传入，如图4所示。因此，在处理数据时，将同一观测点处的损伤铝板信号与健康铝板信号相减，即可只携带损伤信息的信号。

图4 Lamb波在损伤铝板中的传播示意图

3.1 Lamb在健康铝板中传播的有限元分析

本次仿真对象为铝板，其长为400 mm，宽为400 mm，厚为4 mm，密度ρ=2 700 kg/m3,弹性模量E=70 GPa，泊松比υ=0.33。激励信号选择中心频率为250 kHz、周期为5的汉宁窗调制信号。

激励信号的激励点A设置在模型的左端，入射角为45°，观测点B、C分别设置在右上角和左下角,缺陷位置位于板中心，长为12 mm，宽为8 mm。建立的模型如图5所示。

图5 健康铝板的模型图

为了保证结果的稳定性采用显性动力分析，积分单位选取典型代表性的8节点线性减缩单元(C3D8R)。网格划分遵循一个Lamb波波长至少横跨10个网格单元，以达到精度要求[11]。时间步长需满足Lamb波在铝板中传播所花费的时间，根据时间增量准则,激励信号的最大频率对应的最小周期时间必须大于20个时间增量步长[12]。综上所述，最小网格单元长度设置为1 mm,时间步长为3 ms，时间增量步长为40 ns。对设置好的健康铝板模型加载激励信号，并进行数值模拟仿真，计算后分别得到观测点B、C的x-y图,如图6、7所示。

图6 观测点B处健康铝板的Lamb波传播图

图7 观测点C处健康铝板的Lamb波传播图

3.2 Lamb波在损伤铝板中的有限元分析

铝板的参数不变，损伤的位置设置在铝板中心，长12 mm，宽4 mm，激励点与观测点位置不变，建立的模型如图8所示。

图8 损伤铝板的模型图

对设置好的健康铝板模型加载激励信号，并进行数值模拟仿真，计算后分别得到观测点B、C的x-y图如图9、10所示。

图9 观测点B处损伤铝板的Lamb波传播图

图10 观测点C处损伤铝板的Lamb波传播图

为得到只携带损伤信号的x-y图，分别将B、C点的损伤铝板信号与健康铝板信号相减，得到B、C两点的差信号，如图11、12所示。

图11 观测点B处差信号的Lamb波传播图

图12 观测点C处差信号的Lamb波传播图

由图11、12可看出，Lamb波在传播过程中发生多次反射形成叠加，这里使用S0模态的Lamb波信号来进行损伤定位(见图6、7、9～12)。由图1可看出，S0模态下的波速大于A0模态下的波速，即出现的第一个模态为S0模态，将模态的波峰值处的时间作为波在板中的传播时间，通过ABAQUS的x-y图查找功能分别查找各信号的S0模态传播时间和幅值大小，其中差信号表现出仅由损伤引起的传播信号，得到最终数据如表1所示。损伤定位图如图13所示。

表1 ABAQUS仿真数据

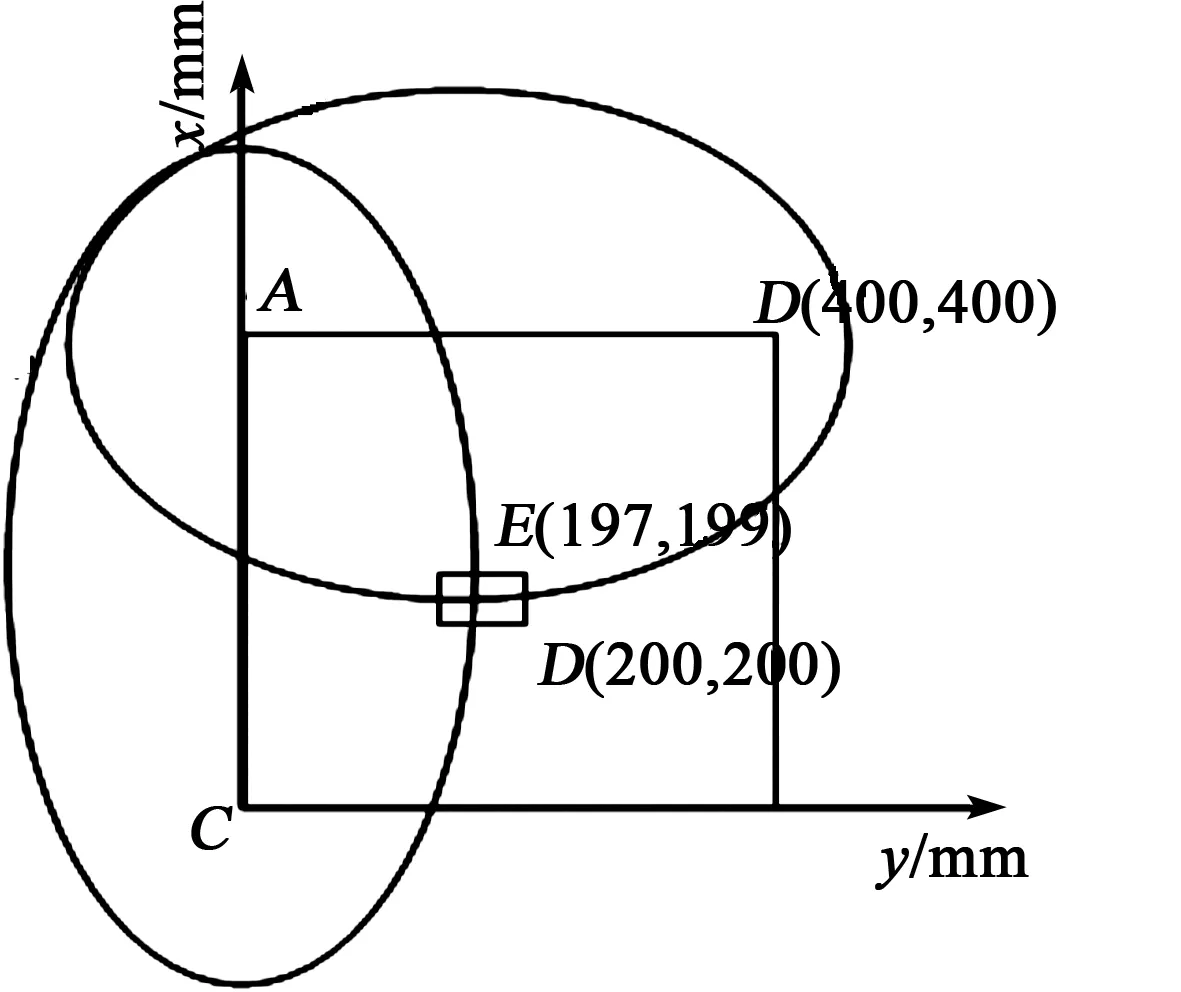
图13 损伤定位图

由图1、2可知，在频厚积为1 MHz·mm处的群速度为5 311 m/s，由S=v·t(其中S为Lamb波的传播距离，v为Lamb波的群速度，t为传播时间)可求出AE+EB=560.3mm，AE+EC=565.8 mm，而所建立的模型中AE+EC=AE+EC=565.7 mm，由此可确定损伤的位置(见图13)。

理论损伤位置E与实际损伤位置D横坐标相距3 mm，纵坐标相距1 mm，误差极小。由图13可知，该模型的检测范围是以A为原点，AC、AB为边界的区域，当损伤位置处于AB或AC线路时，即激励点、损伤点和观测点处于同一直线上，可将模型简化成监测路径上的Lamb波检测。将损伤位置E点至于B点，则监测路径上的损伤定位图如图14所示。提取A点处的x-y图如图15所示。

图14 监测路径上的损伤定位图

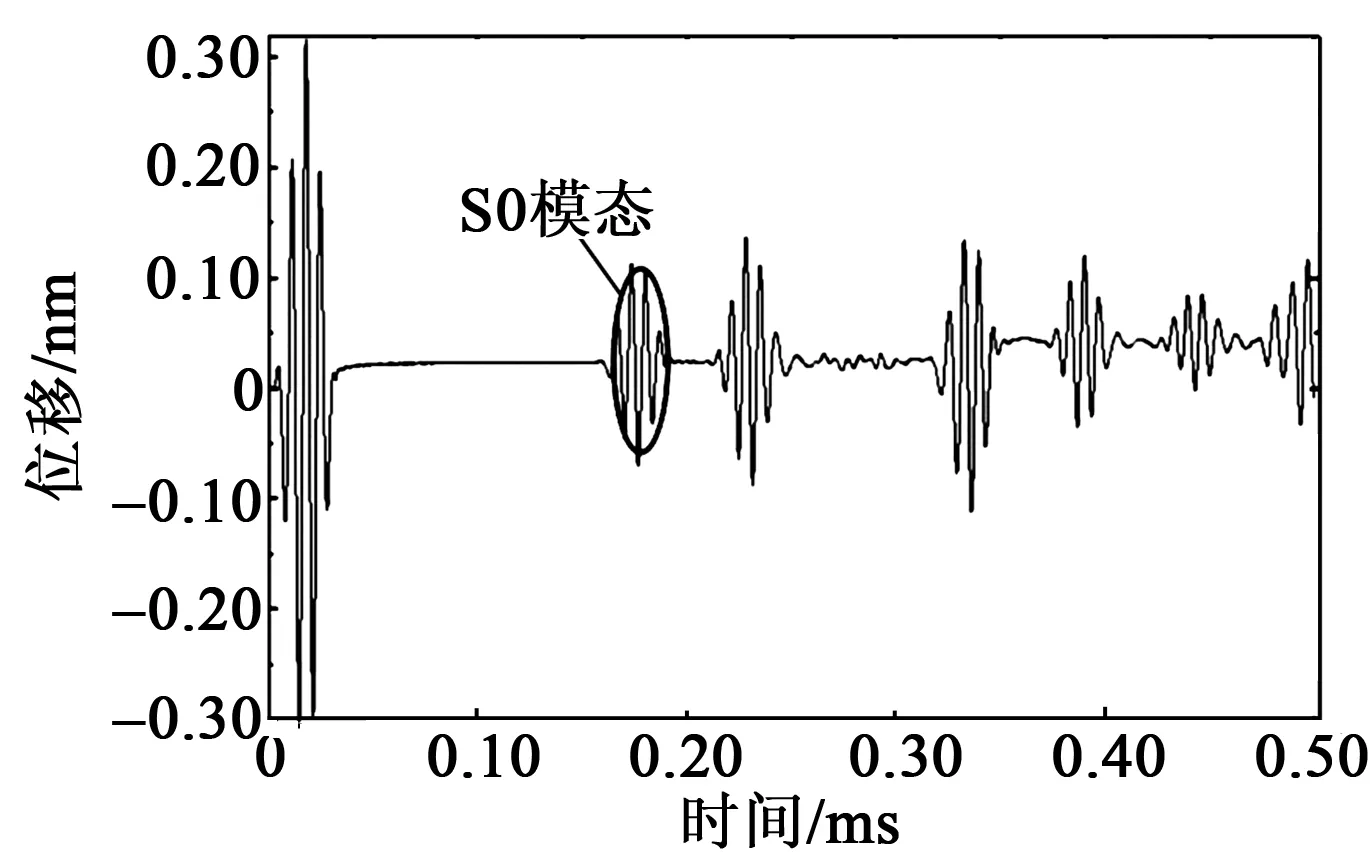
图15 观测点A处的Lamb波传播图

用S0模态来计算传播时间，查询数据点得t=155.97 μs，由S=v·t/2可得S=398.84 mm，与实际位置400 mm很接近。充分验证了本次仿真的可行性，为实验部分奠定基础。

4 结束语

通过研究Lamb波的频散特性，利用ABAQUS建立Lamb波在缺陷铝板中传播的模型并进行分析求解，在尺寸为400 mm×400 mm×4 mm的铝板中识别处出了铝板缺陷大小为12 mm×8 mm的位置并与实际位置进行对比，误差值在5 mm以内，确定了此次仿真的有效性和准确性。充分验证了利用椭圆法对铝板损伤定位识别的有限元模拟的可行性。