超级航姿中基于变阈值判据的自适应Kalman滤波

谢祖辉，杨功流，于东康，李 壮

(1.北京航空航天大学 仪器科学与光电工程学院，北京 100191；2.惯性技术国防重点实验室，北京 100191)

0 引言

机载导航系统通常分为传统航姿系统和惯导系统[1]。超级航姿系统(super-AHRS)作为两者之间的衔接导航系统，它在满足低成本、小体积的同时，还能在主惯导系统和外界辅助信号都失效的情况下，进行短时(20～30 min)较高精度的纯惯导解算，为机载武器的发射提供全面的导航信息。此外，它还能长期输出一定精度的水平姿态和航向信息，以确保飞行器能正确返航。

超级航姿系统通常采用精度水平为0.05 ～ 0.10 (°)/h的光纤陀螺，当GPS失效时，由于陀螺漂移的影响，无阻尼的惯性导航会使飞行器的姿态和航向逐渐发散，导致飞行器无法正确返场[2]。传统捷联航姿系统内阻尼算法虽然在一定程度上能抑制飞行器水平姿态角的发散，但由于加速度计输出特性易受周围环境的影响，因此，基于定阈值的载体机动判据将无法正确判断出飞行器的机动状态，从而导致飞行器的水平姿态长期得不到修正，最终引起姿态角发散[3-4]。当加速度计输出稳定性发生变化时，基于定量测噪声的常规卡尔曼滤波器易振荡甚至发散[5]。

本文提出了一种基于模糊推理系统的变阈值载体机动判据自适应Kalman滤波算法，降低因加表输出稳定性变化所引起的载体机动状态误判率，并提高了滤波稳定性。

1 超级航姿系统内阻尼姿态组合算法

基于载体机动状态自检验的超级航姿系统内阻尼姿态组合算法的基本原理是：由于加速度计长期稳定性好，因此，当载体长期处于非机动状态时，可利用加速度计输出与姿态角之间的对应关系，将计算得到的载体俯仰角θD和横滚角γD作为量测量，通过Kalman滤波器对载体的姿态角进行修正，以提高飞行器水平姿态角精度[6-7]。

1.1 内阻尼姿态角方程

取导航坐标系为东、北、天(E、N、U)地理坐标系，系统比力方程：

(1)

加速度计在载体坐标系下的输出fb与导航坐标系下的投影关系为

(2)

由式(1)、(2)可得

(3)

(4)

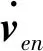
1.2 内阻尼Kalman滤波状态方程

由文献[6,8]知，超级航姿系统内阻尼Kalman滤波的状态量为

(5)

式中：φE，φN，φU为数学平台误差角；δvE、δvN为载体的速度误差；εi(i=x,y,z)为陀螺随机常值漂移。

平台失准角误差模型为

(6)

载体速度误差模型为

(7)

式中：ωN，ωU为地球自转角速率在导航坐标系下的投影；r为地球半径；εE、εN、εU为等效陀螺漂移；fE、fN、fU为加表输出在导航坐标系下的投影。

综上所述可知，超级航姿系统内阻尼Kalman滤波状态方程为

(8)

式中：X(t)为系统状态量；F(t)为误差传递矩阵；G(t)为系统噪声驱动矩阵;W(t)为系统激励噪声序列。

1.3 内阻尼Kalman滤波量测方程

超级航姿系统内阻尼Kalman滤波器中的量测量由惯导解算得到的姿态θI、γI与内阻尼姿态θD、γD之差构成，即

N(t)2×1

(9)

(10)

式中：Z(t)为系统t时刻的量测量；H(t)为系统量测矩阵；N(t)为量测噪声矩阵;θ和ψ分别为载体真实的俯仰角和方位角。

2 变阈值载体机动判据自适应Kalman滤波算法

超级航姿系统内阻尼姿态组合导航算法的关键在于正确判断飞行器的机动状态，适时启用或断开加速度计的量测信息，从而更好地达到校正系统姿态误差，提高系统精度的效果[9-10]。通常情况下，载体机动自检验法以加速度计输出均值作为判断阈值，但当加速度计输出稳定性发生变化且飞行器处于非机动状态时，传统的基于定阈值的载体机动判据将出现误判，从而断开内阻尼姿态修正回路，使载体的姿态角长期得不到修正，最终导致发散。

2.1 基于模糊推理系统的变阈值载体机动自检验法

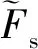
(11)

(12)

(13)

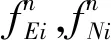
模糊推理系统(FIS)是一种多输入单输出(MISO)或单输入多输出(SIMO)系统，它将确定信号根据知识库转换为模糊量，再将模糊量进行去模糊化处理并转换成精确控制量输出[11-13]。根据最小误判率准则，本文以式(13)作为FIS的输入，以判断阈值d和量测噪声调节因子α作为输出，构成如图1所示的模糊推理系统。其中，输入变量采用全交叠Gauss型隶属函数,而输出变量采用三角形隶属函数，如图2所示。

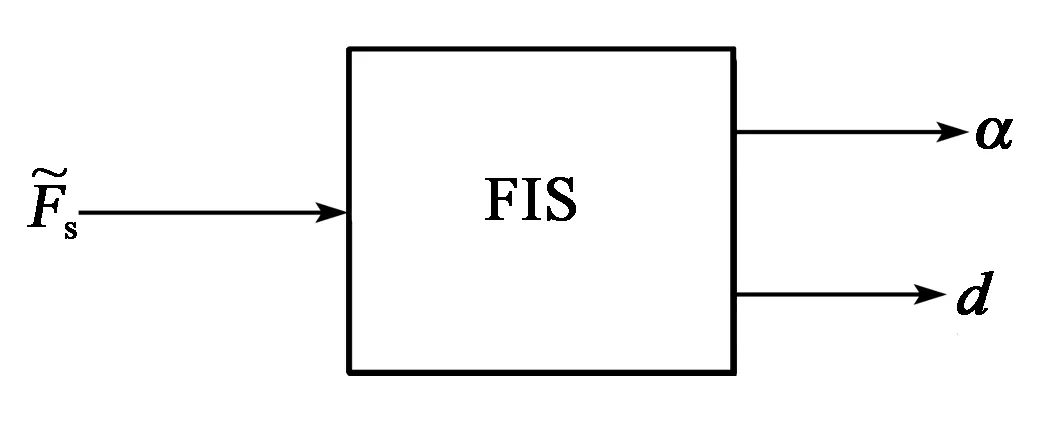
图1 SIMO模糊推理系统

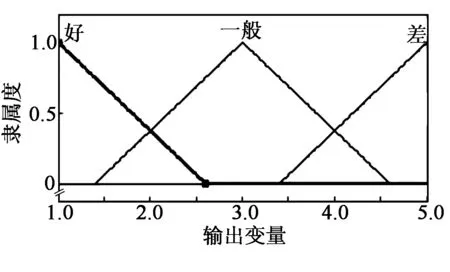
图2 FIS系统输出变量图

在该SIMO模糊推理系统中，用好、一般及差来表示加速度计输出稳定性。根据加速度计输出稳定性越好，内阻尼姿态误差越小的原则，同时，为了减小计算量，方便工程上实时解算，设计3条模糊推理规则如表1所示。

表1 SIMO模糊推理规则

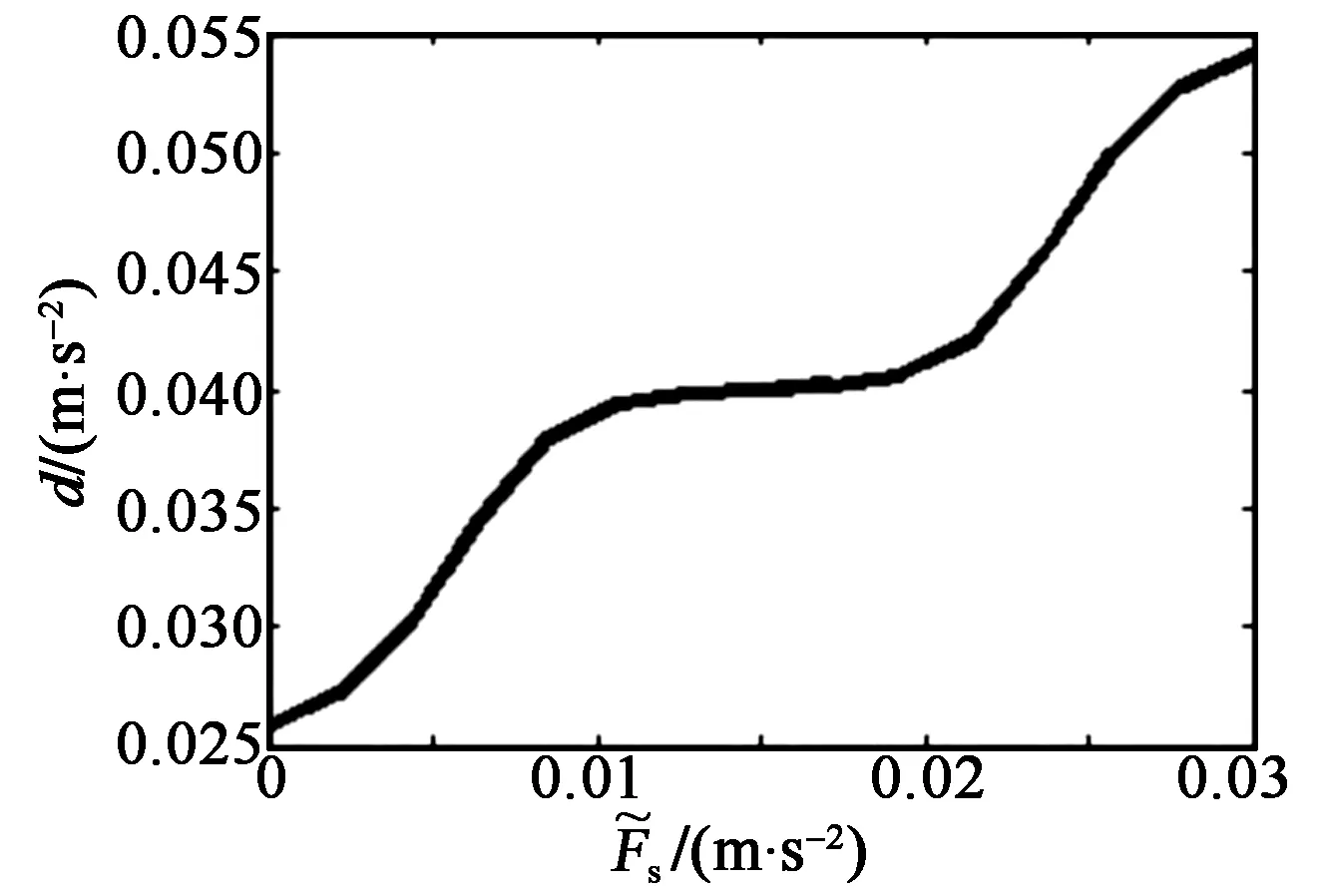
图与d关系图

2.2 基于时变噪声的自适应Kalman滤波算法

变阈值载体机动自检验法虽然降低了载体机动状态的误判率，提高了内阻尼姿态的利用率，但当加速度计输出稳定性发生变化时，基于定量测噪声的Kalman滤波算法无法根据加速度计的输出实时调整量测噪声阵Rk，从而增大或减小Kalman滤波器对量测信息的利用率，严重时将导致滤波器振荡甚至发散[14]。

Rk=αR

(14)

图与α关系图

综上所述可知，本文提出的基于模糊推理系统的变阈值载体机动判据自适应Kalman滤波算法的基本流程为：当由式(11)、(12)计算出的值分别小于d1和d2时(d1和d2均为判断阈值)，即认为载体处于非机动状态，此时启用变阈值载体机动判据自适应Kalman滤波算法来修正载体的水平姿态角，否则系统进入纯惯导解算模式。

3 仿真结果与分析

通过设计两组仿真实验来验证文中所提变阈值载体机动判据自适应Kalman滤波算法的有效性，2组实验的仿真航迹如表2所示。表中，v、a、ω分别为载体的速度、加速度、角速度。

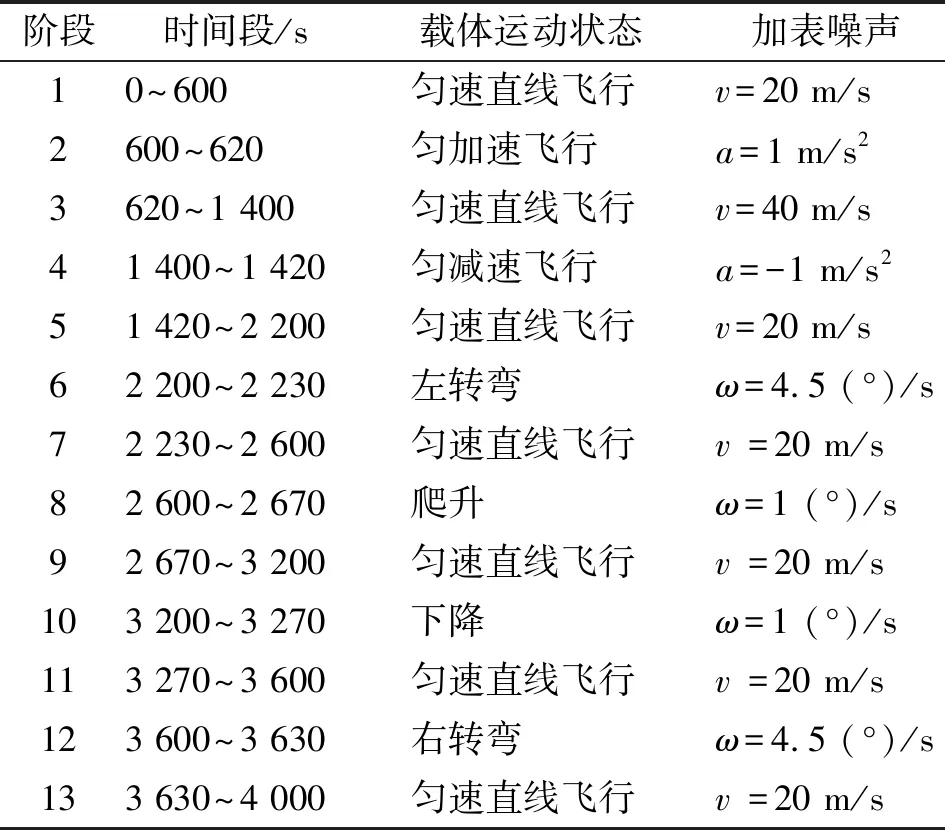
表2 超级航姿系统航迹仿真过程

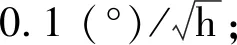
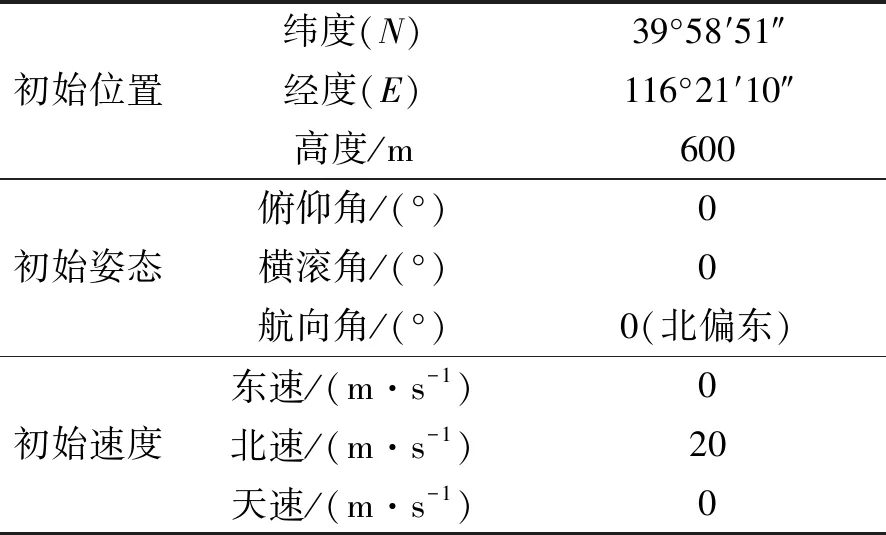
表3 载体的初始状态信息

3.1 变阈值载体机动状态自检法仿真实验

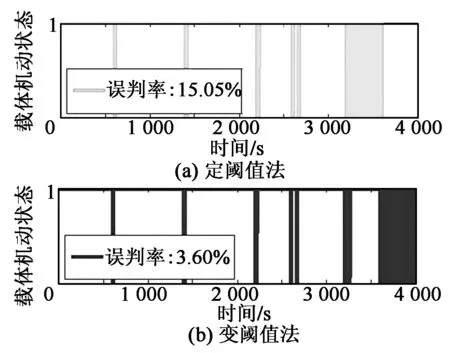
图5 载体机动状态判断结果图

经计算，定阈值法载体机动判据的误判率为15.05%，而变阈值法载体机动判据的误判率仅为3.60%。由图5可看出,在3 200～4 000 s，即加表稳定性突变阶段，基于定阈值的载体机动自检验法明显出现较大的误判率；而基于变阈值的载体机动自检法则能根据加表输出稳定性的高低实时调整判断阈值d的大小，从而降低误判率。由此可见，基于模糊推理系统的变阈值载体机动判据在加表输出稳定性发生变化时，仍能较好地判断出飞行器的机动状态，从而适时启用或断开内阻尼姿态，更好地起到修正载体水平姿态角的作用。

3.2 时变噪声自适应Kalman滤波算法仿真实验

为验证载体水平姿态经过时变噪声自适应Kalman滤波算法修正后的效果，取初始量测噪声阵R=0.02°；根据加表稳定性的高低，将FIS系统另一输出变量α的取值范围设为[0,5]；其余参数及加表随机漂移的变化情况与3.1节相同，得到载体水平姿态误差角曲线和内阻尼姿态角曲线分别如图6、7所示。

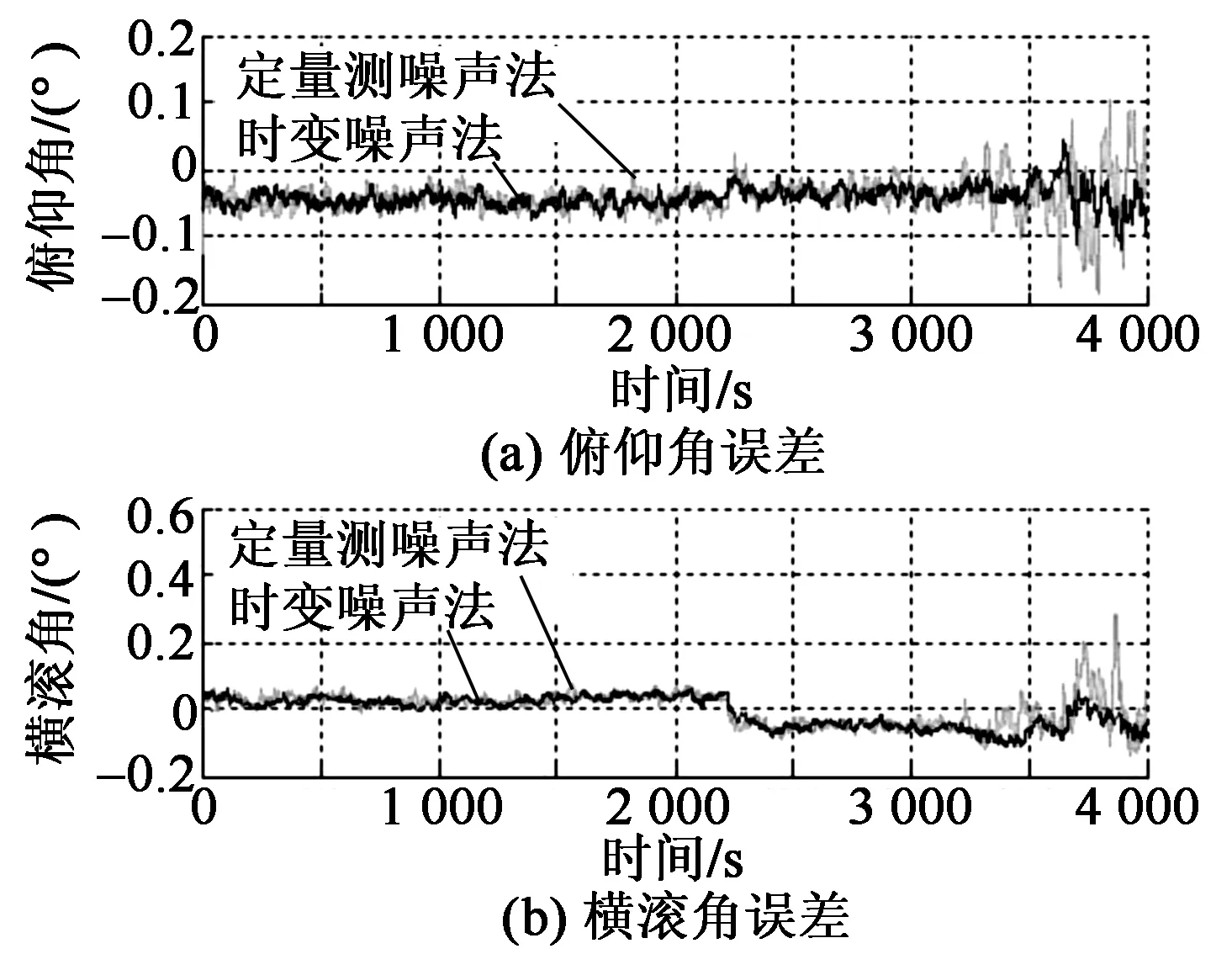
图6 载体姿态误差角曲线

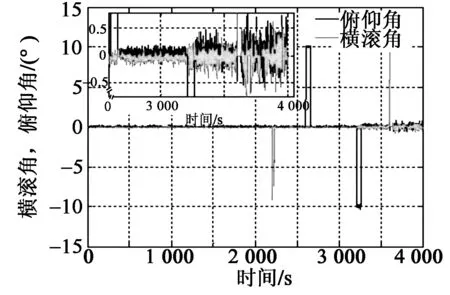
图7 内阻尼姿态角曲线

为了便于直观对比定量测噪声Kalman滤波算法与时变噪声自适应Kalman滤波算法在上述4个阶段的滤波稳定性，各阶段所对应的载体姿态误差角稳定性计算结果如表4所示。

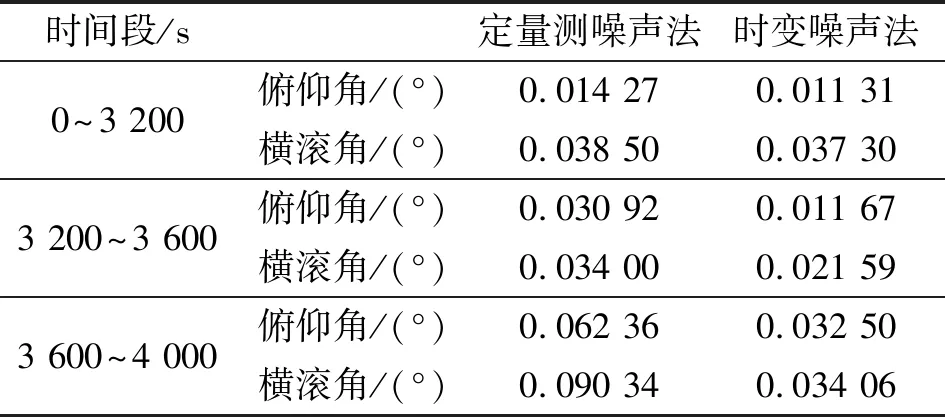
表4 载体姿态角误差稳定性

由图6可见，在0～3 200 s阶段，由于加速度计随机漂移保持不变，两种算法的滤波精度和稳定性基本相同，其中，俯仰、横滚角误差都抑制在0.1°内，且两种算法的姿态误差角稳定性基本相同。在3 200～4 000 s阶段，由于量测噪声发生突变，因此，定量测噪声法出现较大幅度波动，而时变噪声法滤波稳定性明显优于定量测噪声法。其中，在2.5倍噪声时，俯仰、横滚角误差稳定性分别提高了62.26%和36.50%；在5倍噪声时，俯仰、横滚角误差稳定性分别提高了47.88%和62.30%。其原因：由内阻尼姿态融合算法的基本原理可知，加速度计输出稳定性的高低直接决定着内阻尼姿态角稳定性的高低。由图7可看出，加速度计输出稳定性变差的同时，由其解算得到的内阻尼姿态角波动幅度也较大，由于定量测噪声法的量测噪声阵Rk为定值，此时，若初始量测噪声R取值过小，即滤波器的滤波结果对量测信息的依赖程度较高，则Kalman滤波的稳定性随着内阻尼姿态稳定性的变差而变差。时变噪声法能通过FIS系统自适应地调整噪声调节因子α的大小，从而通过式(14)降低超级航姿系统对内阻尼姿态的利用程度，即提高了滤波精度，也增强了滤波器的鲁棒性

4 结论

1) 本文针对传统定阈值载体机动自检法在加表输出时，因受外界干扰导致其稳定性变差，存在对载体机动状态误判率高等缺点，提出了一种基于变阈值的载体机动自检法。该算法不仅能在加表输出稳定阶段正确判断出载体的机动状态，还能在加表输出稳定性发生突变时，通过模糊推理系统自适应调节载体机动状态判断阈值，从而降低了传统定阈值法对载体机动状态的误判率。

2) 本文针对量测噪声发生变化时，传统的基于定量测噪声的Kalman滤波算法滤波稳定性差的缺点，提出了一种基于时变噪声的自适应Kalman滤波算法。该算法以加表输出稳定性作为模糊推理系统的输入，以调节因子α作为输出，实时地对量测噪声阵进行调整，从而提高滤波器对量测信息的利用程度，改善了超级航姿系统在不同状态下的滤波精度和滤波稳定性。

仿真实验表明，本文所提算法能有效抑制超级航姿系统在GPS失效时的水平姿态误差，具有一定的工程应用价值。