一种残差模糊匹配的非线性目标跟踪改进算法

腾红磊，王跃钢，杨 波，单 斌，张复建

(1.火箭军工程大学 三系，陕西 西安 710025；2.火箭军士官学院，山东 青州 262500)

0 引言

近年来，非线性卡尔曼滤波由于其优点而得到国内外学者的深入研究。其中，扩展卡尔曼滤波器(EKF)及其一些改进算法得到较广泛的应用，但需计算雅克比矩阵，且一阶线性化近似精度低[1]。为了克服EKF的理论局限性，Julier等提出无迹卡尔曼滤波(UKF)算法[2]，避免雅克比矩阵的复杂计算，但应对高维数系统存在发散可能。Arasaratnam等[3]使用三阶球面-相径容积法则代替Unscented变换近似计算策略，提出容积卡尔曼滤波(CKF)，并被应用于导航定位、目标跟踪和动态定位等领域[4-5]。上述方法是基于状态先验分布选择确定数目的采样点，并对非线性函数直接传递后的采样点加权处理，以近似获得状态后验概率密度分布，数学意义上统一归为确定采样型滤波器。

非线性卡尔曼滤波在应用于目标跟踪时性能依赖于噪声统计特性和系统模型是否准确，否则引起系统估计误差持续增大，甚至滤波发散。针对先验统计特性未知和估计误差较大约束条件下的EKF算法，通过选择合适的噪声协方差矩阵能提高滤波数值稳定性和收敛速率[6]。因此，学者提出当模型的非线性和噪声先验统计特性满足一定条件时UKF估计误差有界收敛，并指出调整噪声协方差矩阵能确保滤波器收敛[7]。孙妍等将STF算法引入CKF算法框架，提出容积卡尔曼的自适应改进算法(ACKF)，仿真结果证实了可行性[8]。虽然CKF及其相关改进算法能有效提高滤波精度和数值稳定性，抑制滤波发散，但缺少相关的理论对CKF的数值稳定性和滤波收敛性进行系统的分析[9]。

本文基于已获得的非线性算法的收敛性结论，提出一种基于残差的模糊自适应(RTSFA)非线性目标跟踪算法，利用李雅普诺夫第二方法给出算法收敛的充分条件，将T-S模糊逻辑和量测椭球界限规则引入非线性跟踪算法，最后给出RTSFA算法的具体流程。

1 RTSFA目标跟踪算法机理

假设非线性离散系统和量测模型描述如下：

xk+1=f(xk,uk)+ωk

(1)

yk+1=h(xk+1)+νk+1

(2)

式中：xk∈Rn为k时刻系统的状态向量；uk∈Rp为控制向量；yk∈Rm为量测向量；ωk∈Rn，νk∈Rm分别为零均值且线性无关的高斯白噪声；函数f(xk)和h(xk)分别为状态和量测的非线性函数。

首先，定义估计误差和一步预测误差为

(3)

(4)

这里基于文献[10-11]对误差表达式进行简化：

(5)

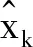
因线性化近似时忽略了高阶项，为了得到严格的预测误差等式，这里定义2个未知对角矩阵βk=diag(β1,k,…，βn,k)，αk=diag(α1,k,…，αn,k)，使得下式成立：

(6)

(7)

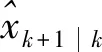
由Sigma点卡尔曼滤波(SPKF)算法[12]可得，系统滤波满足高斯分布积分：

(8)

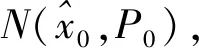
(9)

(10)

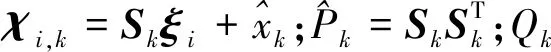
量测预测及协方差、互协方差为

(11)

(12)

(13)

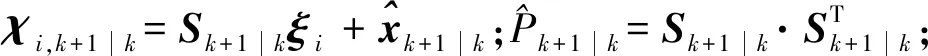
状态更新及协方差、卡尔曼增益为

(14)

(15)

(16)

由式(3)、(4)、(15)易得

(17)

整理式(17)、(7)，代入(6)可得

(18)

因此，可求得预测误差协方差为

(19)

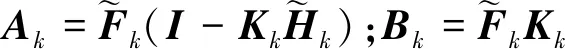
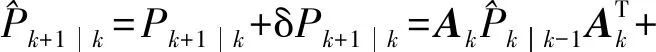
(20)

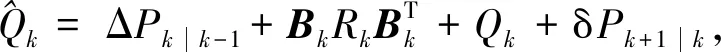
(21)

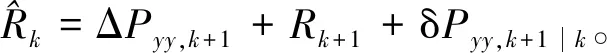
(22)

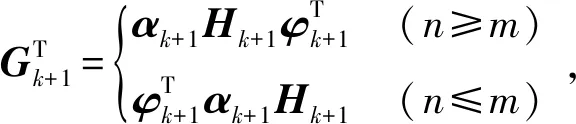
(23)

(24)

通过定义未知的对角矩阵，给出基于SPKF基本框架且含有线性误差的系统滤波严格形式，下面进一步分析RTSFA算法机理收敛的充分条件。

2 RTSFA目标跟踪算法机理收敛性分析

对式(3)的估计误差进行分析，下面不加证明的给出关于随机过程有界性的结论[14]：

引理 1 假设存在随机过程Vk(ηk)，实数vmin，vmax，μ>0，0<λ≤1，使得随机过程ηk的每个解都满足下式：

vmin‖ηk‖2≤Vk(ηk)≤vmin‖ηk‖2

(25)

E[Vk(ηk)|ηk]-Vk-1(ηk-1)≤μ-λVk-1(ηk-1)

(26)

则随机过程均方指数有界，即

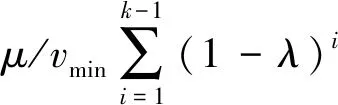
(27)

为证明过程更准确，有如下假设：

假设1 非线性系统(见式(1)、(2))对于k≥0，存在umin,umax,smin,smax,βmin,βmax,αmin,αmax,φmax≠0使以下不等式成立：

(28)

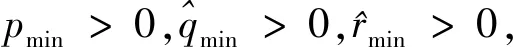
(29)

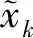
证明：定义李雅普诺夫函数：

(30)

(31)

(32)

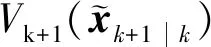
(33)

(34)

根据假设条件1、2的各界限值可得

(35)

将式(35)代入式(34)，并分别对不等式两端求逆：

(36)

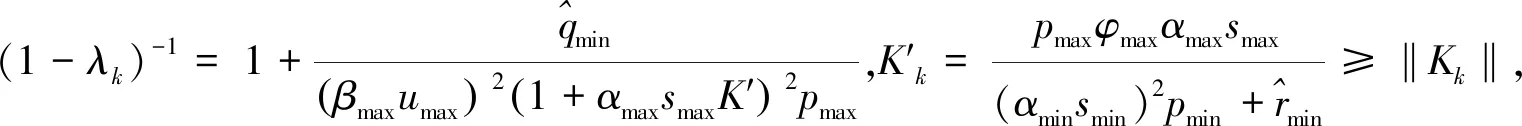
(37)

(38)

考虑恒等式tr(UV)=tr(VU)，对式(38)两端求迹，存在实数μk>0，且在假设条件下有界。将式(36)代入式(37)可得

(39)

(40)

(41)

联合假设1、2的各界限值可得

(42)

3 RTSFA目标跟踪算法步骤及应用

根据上述的收敛性结论，结合式(10)、(12)，Rk和Qk的值成为关键。因此，引入自适应协方差矩阵，构造自适应Rk和Qk如下[10]：

(43)

(44)

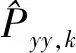
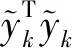
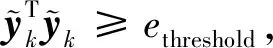
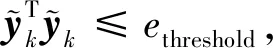
采用单点模糊产生器[15]，确定2个模糊集：D为减少，I为增加。选择T-S模型设计推理引擎，ρ和σ的变化逻辑关系通过Qk和Rk的递推关系为

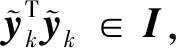
(45)

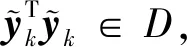
(46)

2) 根据式(43)、(44)，本文构造的自适应状态方程噪声协方差和量测方程噪声协方差仅与残差有关，当出现异常量测更新时会产生较大残差。因此，这里选择量测椭球界限规则确定量测空间的有效区域，用于判定异常量测野值，描述如下：

(47)

式中γG为界限阈值，可从χ2状态分布中得到[16-17]。

RTSFA的非线性目标跟踪算法总结如下：

a.初始化后验概率密度函数

(48)

b.时间更新

4) 根据式(47)进行判定，不满足则按下式进行更新：

(49)

若满足则进行下一步。

6) 重复执行算法步骤2)～5)。

4 仿真实验

4.1 实例1：滤波初值信息不明纯方位跟踪

二维笛卡尔坐标系下，假设雷达测站位于坐标原点，目标在空间内沿方向角30°做近似匀加速直线飞行，目标运动模型的状态方程描述为

xk+1=Fkxk+ωk

(50)

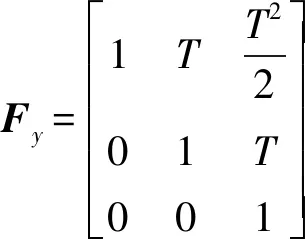
(51)

(52)

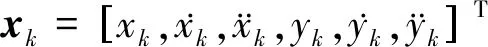
目标运动的量测方程为

(53)

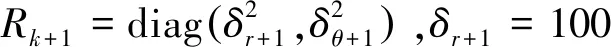
假设目标的理论初始位置为[200 0]，初始速度和加速度分别为10 m/s、2 m/s2。为了验证初始状态偏差较大时算法的性能，设置滤波器的初始状态x0=[10 30 10 50 10 10]T，初始协方差矩阵P0=10-2I6，δ和ζ分别取10-6和10-4，仿真数据产生步数N=100。

首先，分析不同调节因子的影响，以x方向加速度信息为对象，取调节因子ρ和σ为常量102、104和模糊值，并与CKF进行对比，结果如图2所示。在初始状态存在较大偏差时，CKF失去跟踪能力，虽然能够基本收敛但滤波精度下降且收敛较慢。104RAKF(RAKF为残差自适应卡尔曼滤波)和RTSFA较CKF明显具有较快的收敛速度，并减少由初始状态不准确引起的估计误差。尽管两者能克服滤波发散，但随着估计误差的减小，RTSFA的模糊自适应调节因子相比于常量调节因子具有更高的滤波精度。102RAKF较104RAKF(调节因子为102和104常值的RAKF)具有更高的滤波精度，但其选择较小的调节因子，其收敛速度不理想。

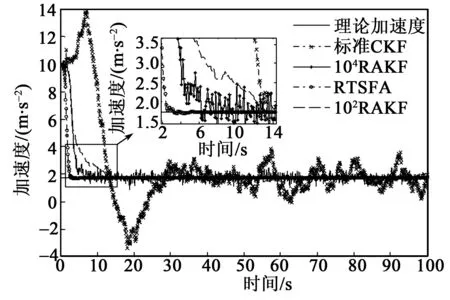
图1 初始状态偏差较大时x方向加速度估计曲线

其次，为了更好的对比算法性能，使用加速度信息定义的均方误差均值：

(54)

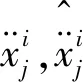
表1 几种算法下x方向加速度均方误差均值

当系统初值不明甚至存在较大偏差时，RTSFA的算法跟踪性能优于其他确定采样卡尔曼滤波器，尤其是与常量调节因子的卡尔曼滤波相比具有更快的收敛速度，并能在估计误差减小时确保估计值更接近真实值。

4.2 实例2：量测噪声时变纯方位目标跟踪

基于实例1的仿真环境，目标在空间内以一定角速度做机动转弯，运动量测方程和噪声特性形式仿照实例1定义，目标运动模型的状态方程描述为

xk+1=Fkxk+Γωk

(55)

(56)

(57)

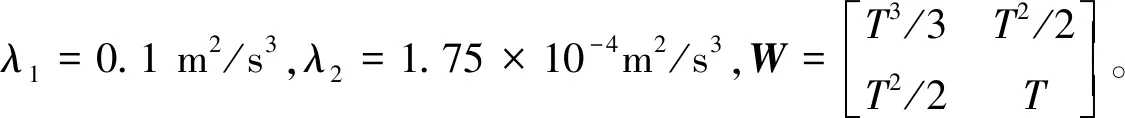
(58)

在量测噪声时变的条件下，图2～4分别为4种算法跟踪目标的位置、速度和角速度的均方根误差结果。在目标跟踪30 s内，量测噪声与先验量测噪声相对一致，4种滤波估计误差相差不大。

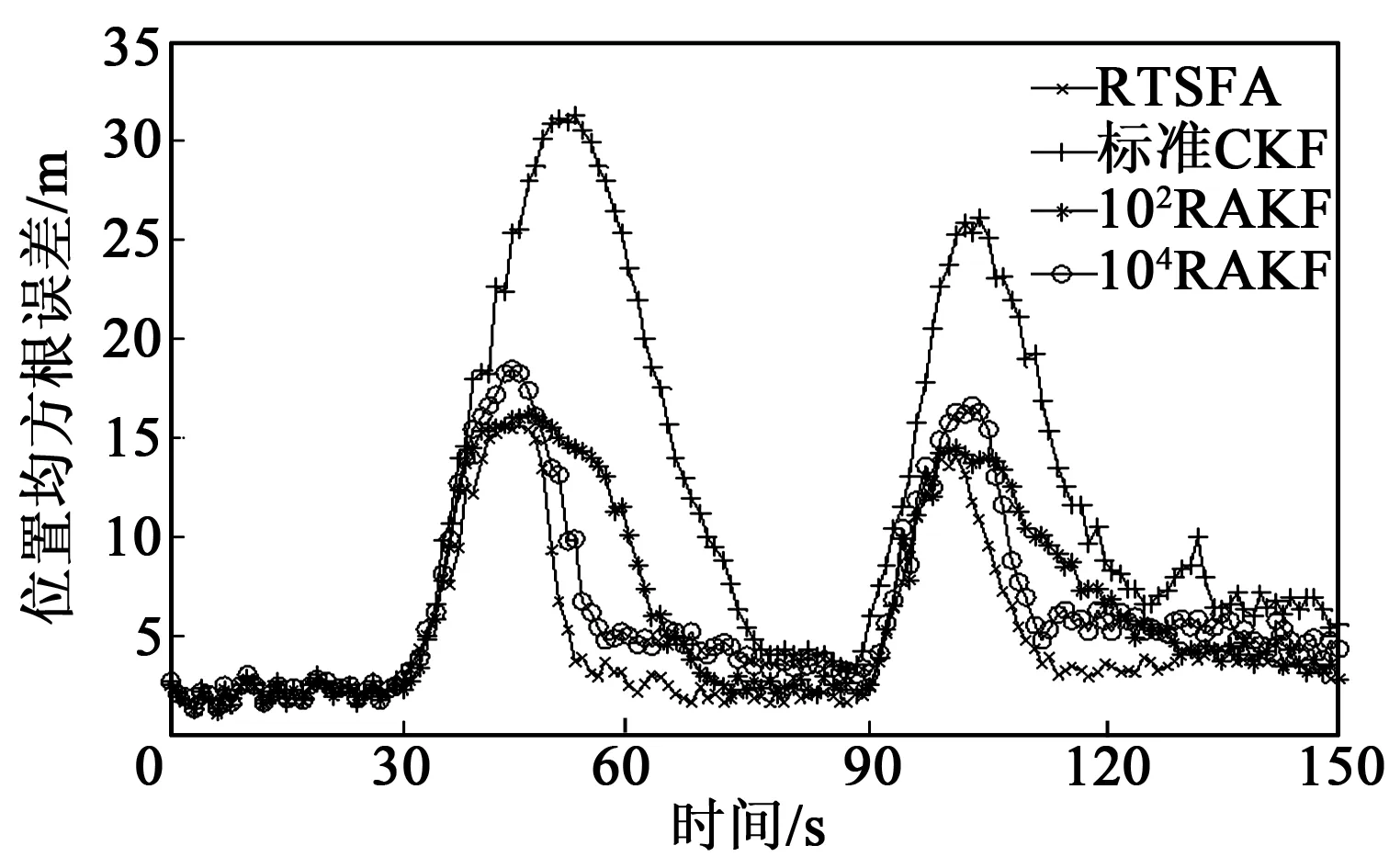
图2 4种算法下位置的均方根误差

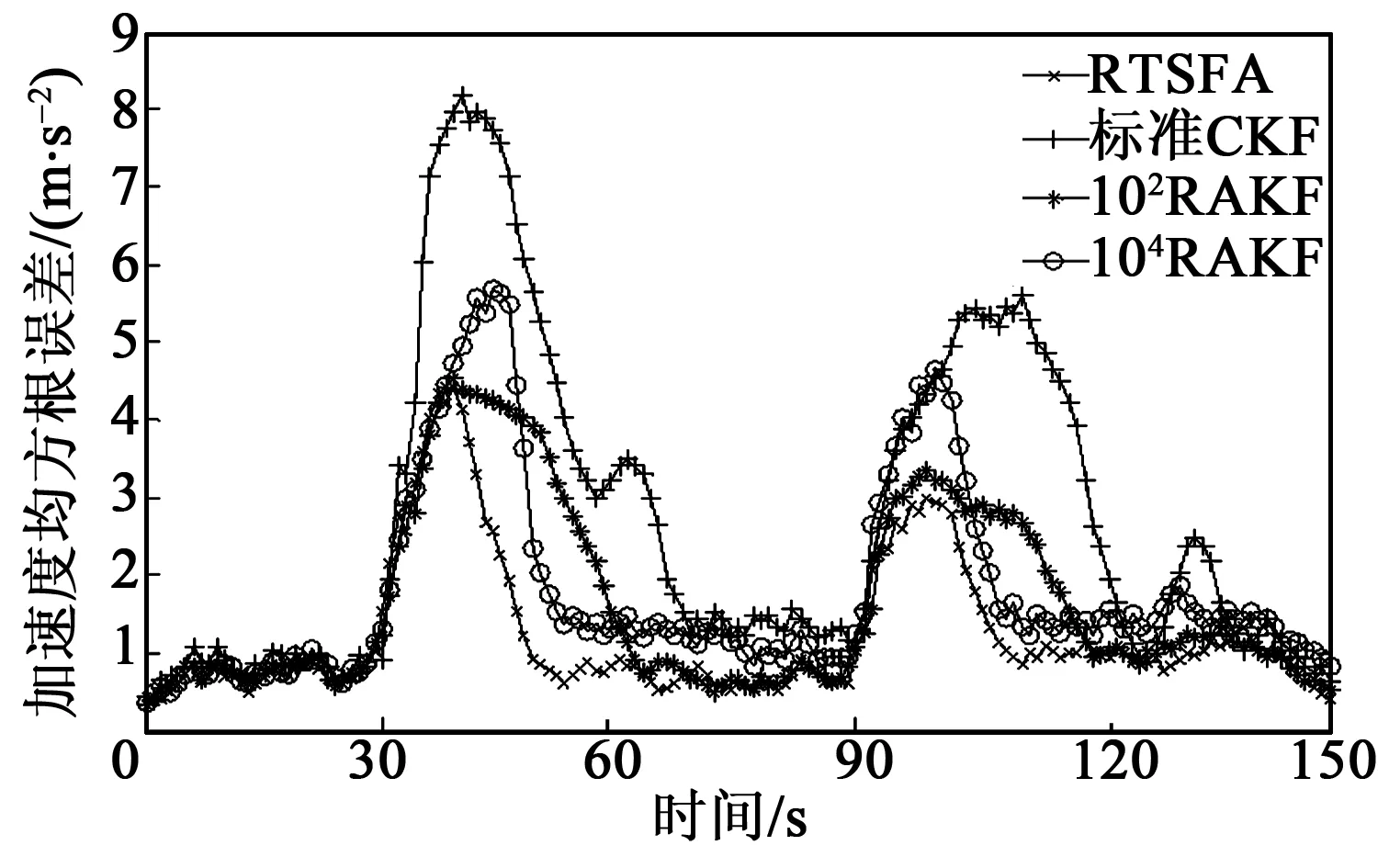
图3 4种算法下加速度均方根误差

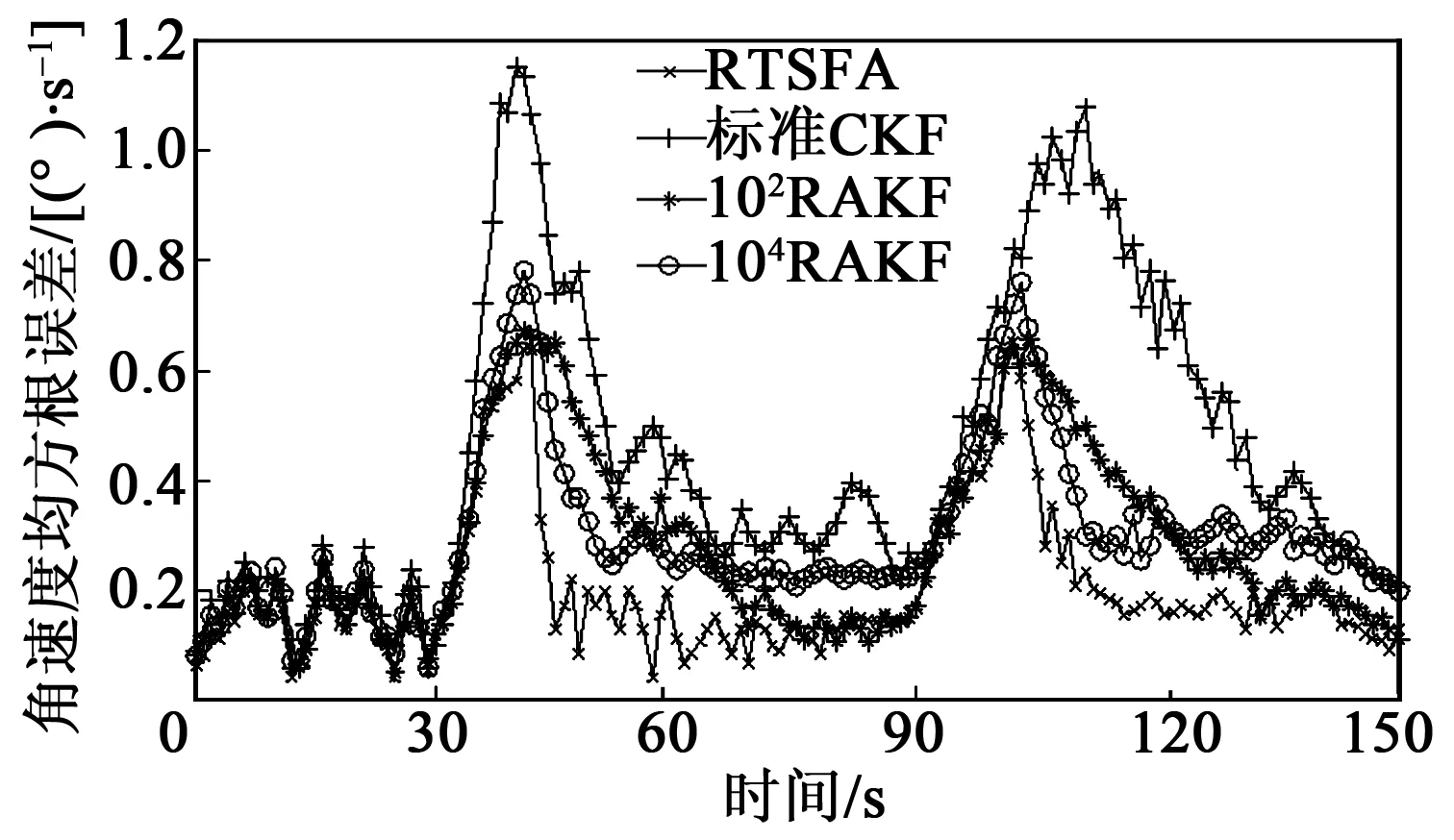
图4 4种算法下角速度均方根误差

在31～90 s和91～150 s时量测噪声发生变化，先验量测噪声协方差不能对系统量测噪声进行准确数学描述，4种算法估计误差都开始迅速变大。与其他3种算法相比，标准CKF算法不具备调整量测噪声协方差的能力，估计误差随时间更新逐步加大，滤波精度下降，收敛较迟缓；102RAKF采用较小调节因子，能有效提高滤波精度，避免滤波发散，但收敛较缓慢；104RAKF收敛快，但收敛后精度较差。表2为4种算法的状态估计均方根误差均值统计数据。

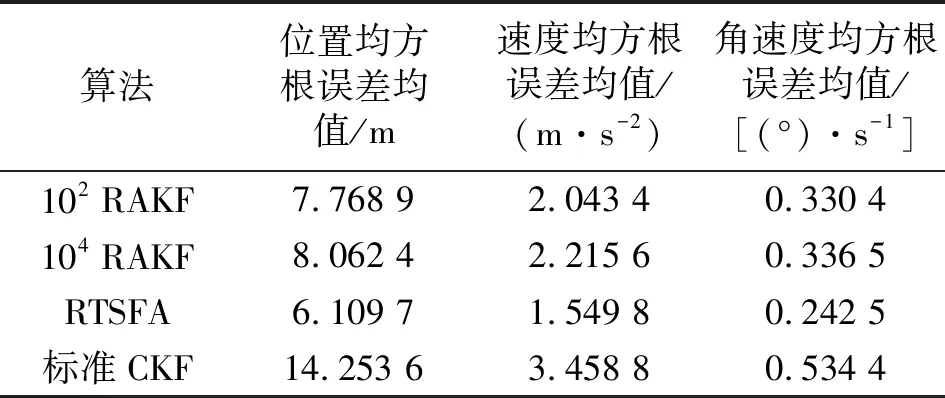
表2 4种算法下状态估计均方误差均值

RTSFA算法基于量测残差和模糊逻辑递推量测噪声协方差阵，使R更接近真实值，克服时变噪声统计特性引起的滤波发散问题。由图2～4及表2可知，本文算法的滤波估计精度和收敛速率优于其他3种算法，跟踪数据更接近真实值。

5 结论

1) 提出一种基于残差的模糊自适应(RTSFA)非线性目标跟踪算法。该算法根据Sigma点卡尔曼滤波(SPKF)的基本框架和球面径向规则推导出线性化误差约束条件下的近似高斯权值积分一般形式。同时，利用李雅普诺夫第二方法证明了RTSFA非线性目标跟踪算法估计误差有界收敛的充分条件，并构造一种噪声估计器在线修正噪声统计特性，引入T-S模糊逻辑算法和量测椭球界限规则选择准确的自适应噪声协方差调节因子，有效抑制传统非线性跟踪算法因噪声统计不准引起的滤波发散，增强非线性滤波器应对目标跟踪的鲁棒性。

2) 将本文算法应用于信息不明和量测噪声时变纯方位目标跟踪中进行仿真验证，在目标因初值误差和量测时变引起估计误差变大时，与其他确定性采样卡尔曼滤波器和常量调节因子的残差自适应卡尔曼滤波相比，该方法具有更强的鲁棒性和更快的收敛速度，表现出更好的跟踪能力。