口齿式定子驱动的平面超声电机特性分析

余 九，贺红林

(南昌航空大学 航空制造工程学院,江西 南昌 330063)

0 引言

超声电机是一种利用逆压电效应将电能转换为机械能的新型压电换能结构。与传统电机相比，压电超声电机具有低噪、微型化，可控性好，抗干扰性好等优点，在航空航天、智能制造及精密仪器等方面已得到广泛应用。超声电机分有旋转型、直线型、单自由度及多自由度等形式。1998年,Tomikawa等[1]利用矩形板面一纵和四弯进行电机驱动，该电机在NEC实现了产业化。1999年,日本多生电机利用三角形压电振子实现了薄型电机[2]，其速度达450 mm/s。2010年,Won-Hee Lee等[3]提出了一种外型类似于碟翼的微型超声电机，其体积为9 mm×8 mm×1 mm。2003年,李朝东等[4]推出了卧板式大动力电机。2006年,赵淳生等[5]推出方板两正交二弯模态驱动的电机，速度为180 mm/s，推力为5 N。2008年,李宝玉等[6]实现该型的单足驱动到双足驱动的转换。2014年，刘英等[7]设计了多种基于纵弯复合模态的多自由度电机，最大直线速度为1 182 mm/s。总体看来，由于发展时间不长，现已推出的平面超声电机型式有限[8-9]，电机性能离产业化还有很大差距。一方面，超声电机普遍存在动力小，效率低，工作欠稳定等问题，故而深入探析其力/电转换行为、摩擦驱动机理、理论建模和结构优化成为其重要研究内容[10-11]。另一方面，由于电机较有限的结构形式，无法满足应用领域对其提出的多样需求，故探索电机新原理及定子超声换能结构仍是直线电机研究的重要方面[12]。因此，为丰富平面超声电机的型式，本文提出口齿形定子驱动的平面超声电机，对电机的振动驱动机理、动力学优化及运行特性等进行了研究。

1 电机运动原理及设计

1.1 定子工作模态及结构

电机定子采用口齿形结构(见图1(a))，由外框和内部对称的4根条状齿组成。在每根杆正反面末端位置均设置驱动足，齿的正反面和左、右侧面分别设置面内激振压电陶瓷片和面外激振压电陶瓷片。选取定子面外弯振、横齿面内弯振、纵齿面内弯振为电机的工作模态。面外弯振分别与横齿面内弯振、纵齿面内弯振耦合，分别在横齿、纵齿驱动足上合成出沿xOz、yOz面行进的椭圆轨迹，以推动电机沿x、y向移动，从而实现平面运动。

图1 平面电机的定子子结构及其工作模态

1.2 定子压电陶瓷激励配置

根据定子工作模态振型，为其配置的压电极化供电方式如图2所示。

图2 定子上压电陶瓷的极化及其供电配置

图2中，采用正弦信号sinωt激励横齿面内弯振和纵齿面外弯振，余弦信号cosωt激励横齿面外弯振和纵齿面内弯振，这使横、纵齿面的内、外弯振响应的相位差皆为90o。各陶瓷片均沿背离粘贴面方向极化，且各陶瓷片与定子基体粘结的电极均接地以避免短路。为增强各工作模态的振幅，将各陶瓷片(PZT)尽量贴在弯振模态波峰(谷)处。

1.3 电机驱动机理

图3为纵齿在1个振动周期(T)内推动动子运动的情形。

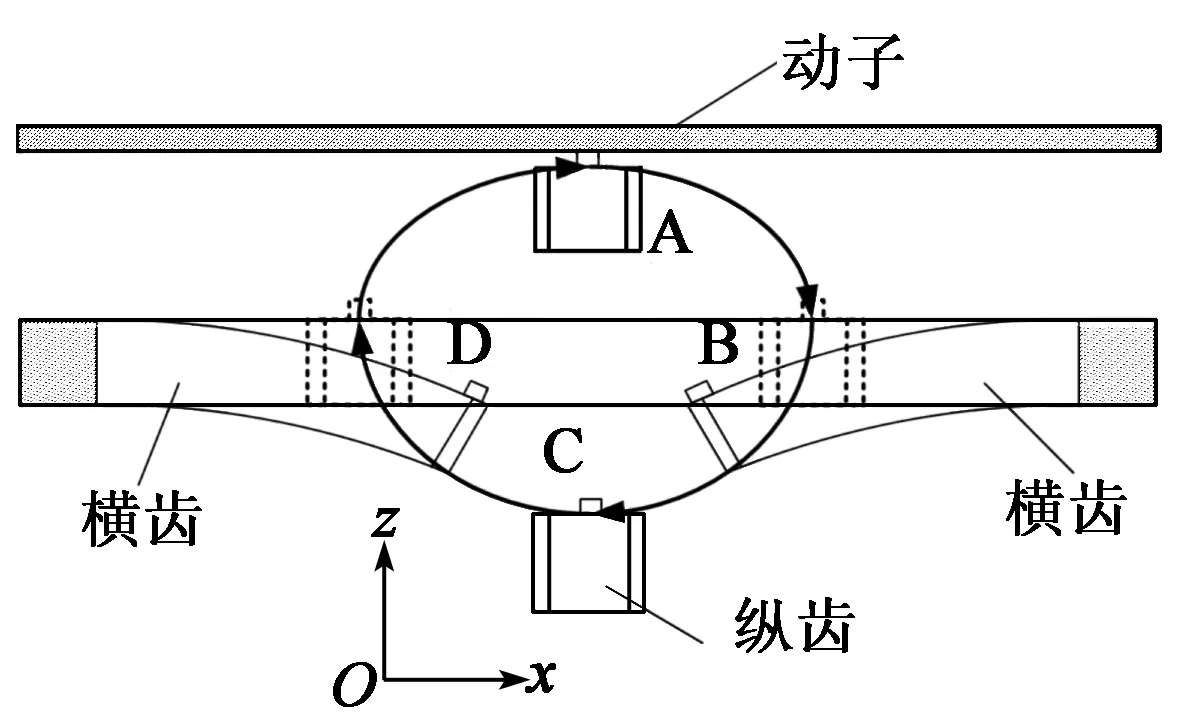
图3 定子在一个振动周期内运动

运动具体如下：

1) 在0～T/4振动时段内，定子面外弯振使纵齿由最大前弯状恢复成直杆状，纵齿上的驱动足与动子接触,而此时横齿由最大后弯状恢复成直杆状，且与动子不接触；定子面内弯振使纵齿由初始位置A行至B处。在该时段，纵齿上部驱动足与动子接触，推动动子沿x向移进第一个步距。

2) 在T/4～T/2振动时段内，定子面外弯振驱使纵齿由直杆状弯成最大后弯状，纵齿上的驱动足与动子脱离接触。此时，横齿由直杆状弯至最大前弯状，且横齿上的驱动足与动子接触；定子面内弯振使纵齿由位置B行至最大后弯曲处C。在该时段，定子横齿上的驱动足与动子接触，推动动子沿y向移进第二个步距。

3) 在T/2～3T/4振动时段内，定子面外弯振使纵齿由最大后弯状恢复成直杆状，同时纵齿上的驱动足与动子保持脱离。此时，横齿由最大前弯状恢复至直杆状，且横齿上的驱动足与动子保持接触。定子面内弯振使纵齿由最大后弯处C行至D处。在该时段，横齿上的驱动足与动子接触，推动动子沿y向移进第三个步距。

4) 在3T/4～T振动时段内，定子面外弯振使纵齿由直杆状弯成最大前弯状，纵齿上驱动足与动子接触。此时，横齿由直杆状弯至最大后弯处，且横齿上的驱动足与动子脱离。在该时段，定子面内弯振使纵齿由D处行至最大前弯处A。在该时段，纵齿上的驱动足与动子接触，推动动子沿x向移进第四个步距。

2 结构动力学优化

2.1 定子有限元(FEM)建模

对于结构、边界条件简单的圆板或矩形板，可用解析法求取振型及其振动响应，但对于口齿形这样的复杂结构，则只能进行数值法求解其动力学特性，本文采用FEM模型如图4所示。定子的FEM模型动力学平衡方程为

(1)

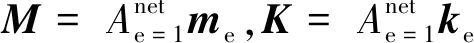
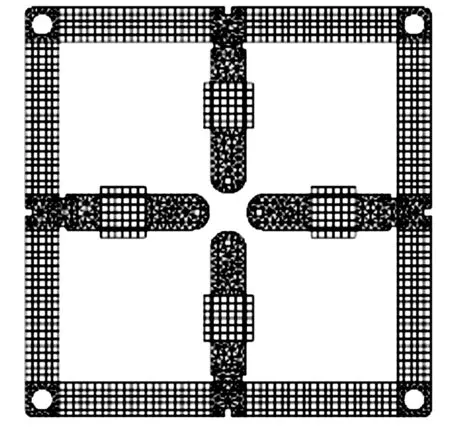
图4 定子FEM模型

利用ANSYS求解式(1)时，采用Solid185对定子基体网格化，采用Solid5对PZT网格化。定子材料采用磷青铜，材料密度为8 270 kg/m3，弹性模量为92.0 GPa，泊松比为0.33。压电陶瓷材料选PZT8。

2.2 频率灵敏度分析

定子两相工作模态的频率应尽量接近，且振型应尽可能纯正，这样才能在驱动足激发出足够的振幅以驱动动子。为此，对定子做频率一致性优化设计。优化前，需先对定子做频率灵敏度分析，频率灵敏度是指单位尺寸变化所引起的频率变化，定义：

(j=1,2,…,6)

(2)

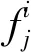
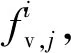
表1 优化前、后定子尺寸

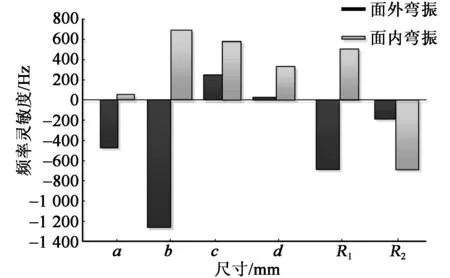
图5 振子结构尺寸的频率灵敏度

根据图5优化定子尺寸得到定子优化后尺寸如表1所示。根据优化后的尺寸得到定子的三相工作模态(见图1(b)～(d))频率分别为31 347 Hz、31 350 Hz和31 356 Hz，最大频差为9 Hz，不超过模态频率的0.03%，频率一致性良好。定子三相模态振型纯正，有利于振子振动响应控制。

3 定子振动响应及运动调节

3.1 谐响应分析

谐响应分析可判断定子工作模态附近是否存在干扰模态，并为剔除干扰模态确保电机正常运行提供依据。因为干扰模态的存在将导致电机无法正常运行。对定子的FEM模型施加250 V的简谐电压，设置频率分析范围为30.9～31.5 kHz，在频率分析范围内设置100个频率分析点对定子做谐响应分析,得到的驱动足幅频特性如图6(a)所示。由图可见，驱动足在x、y、z向均只出现单个峰值，均未出现干扰模态，这说明口齿型定子具有良好的驱动特性。定子只有以最适频率驱动，才能产生最大振幅，使电机性能最优。因此，对频区30～32 kHz进行细化扫频，得到定子最适驱动频率为30 800 Hz。

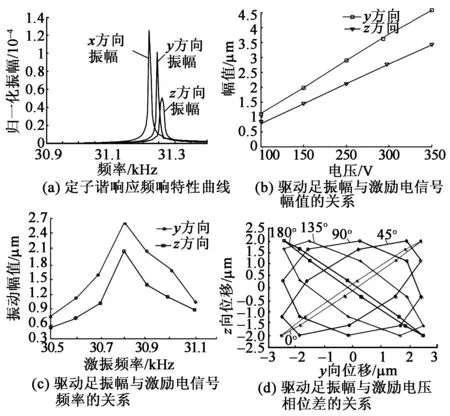
图6 定子频响及运动调节特性

3.2 瞬态振动特性

3.2.1 瑞利阻尼的选择

在求解定子瞬态振动特性时，必须先设置定子结构的瑞利阻尼，否则求解将不会收敛。瑞利(Rayleigh)阻尼假设结构的阻尼矩阵C是质量矩阵M和刚度矩阵K的组合，即

C=αM+βK

(3)

Cn=αMn+βKn

(4)

式中Cn，Mn，Kn分别为第n阶振型的阻尼系数、振型质量和刚度，且

(5)

(6)

(7)

瑞利阻尼是一种正交阻尼。假设结构体系的阻尼满足正交条件，并采用振型叠加法求解，则不必构造整体阻尼，而直接采用振型阻尼比εn即可，因为实际结构阻尼测量中都是直接给出阻尼比，即

Cn=2εnωnMn

(8)

(9)

将式(8)、(9)代入式(4)可得

(10)

如果给定任意2个振型阻尼比εn分别代入式(10)，即可得关于α和β的2个线性代数方程，解得α和β，则确定了瑞利阻尼。假设εi和εj给定，则可计算出α和β的矩阵形式为

(11)

得到其解析式为

(12)

由谐响应分析可知，口齿形定子的最适驱动频率为30 800 Hz，这里取ωi=30 750 Hz，ωj=30 850 Hz，εn=0.005，代入式(10)求解，由式(12)可得瑞利阻尼为

(13)

3.2.2 瞬态特性求解

只有定子驱动足振幅达到微米级别，定子的振动才能通过摩擦转换为动子的宏观运动。为此，在定子FEM模型的两相PZT施加30 800 Hz、250 V等幅、同频且相位差为π/2的交变电压，且施加第3.2.1节所求得的阻尼，启动ANSYS瞬态解算器，求得纵齿和横齿的椭圆运动轨迹如图7所示。可见，定子面内、外工作模态均被有效激励，驱动足产生了微米级振动，其x、y、z向振幅分别达2.1 μm、2.6 μm、2.0 μm，电机有望得到较好性能。

图7 定子定频激励时驱动足运动轨迹

3.3 电机运动调节特性

压电平面电机的优势之一便是多样化的振动调节特性。考虑到电机采用简谐信号驱动，故分别就驱动信号的幅值、频率、相位差对驱动足运动的影响进行探索。首先对定子模型施加不同幅值的驱动电压，得到驱动足调压特性如图6(b)所示。由图可见，驱动电压幅值与驱动足振幅呈现一定线性关系，增大电压,驱动足切向、法向振幅也相应地增大。

采用等幅、不同频率的驱动信号激励定子模型，得到驱动足振幅与驱动频率间关系如图6(c)所示。由图可见，当驱动频率低于工作模态频率时，增大驱动频率，则电机振幅增加，但当驱动频率高于工作模态频率时，增大频率却使振幅快速下降，这是因为驱动频率与工作模态频率不等时，驱动足产生差拍振动现象，拍频率恰为驱动频率与激励频率的差，差拍振动导致驱动足振幅减小。

对定子面内、外弯振激励陶瓷片施加不同相位差的电信号，得到驱动足振幅与相位差间关系如图6(d)所示。由图可见，当相位差为90°时，驱动足轨迹为规范的椭圆；当相位差为45°时，驱动足轨迹变为倾斜态扁椭圆；当相位差为0°时，驱动足轨迹退化为斜直线。所以，要以调相法调节电机振幅，驱动信号相位差只能控制在90°附近较小的区域，否则电机可能无法正常工作。

4 装配结构设计

图8为电机装配结构。支座上有螺纹孔，用以固定支座在别的机械结构上；盖板上设置球槽和安装孔，预紧滚珠安装在盖板球槽内，以减小摩擦阻力，盖板通过螺钉固定在支座上；定子通过螺栓和弹性垫片固定在支座上。

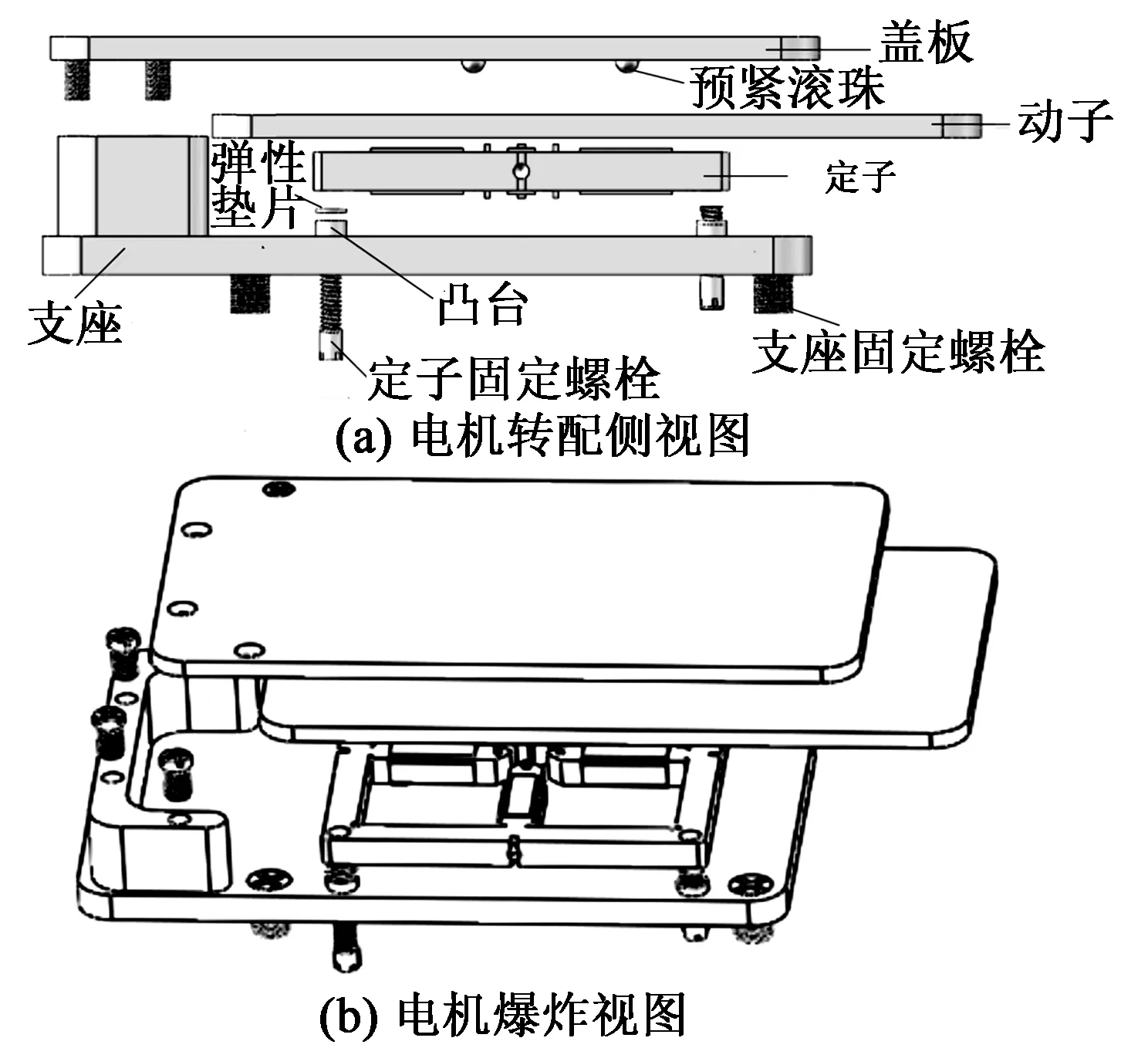
图8 电机装配结构设计

由于定子的4个端部恰为工作模态的节点，故在装配结构选定四端部圆孔作为定子的固定点，因为在该处将定子固定将对定子工作模态产生最小的影响，在该处用螺钉将定子固定。考虑到振子需做面外弯振，故为防止驱动足触碰支座底板而影响振子振动，故在支座上设置高度为1～2 mm的凸台。动子下表面与定子驱动足接触，同时与顶部盖板通过滚珠构成滚动副连接。电机通过螺栓、预紧滚珠和弹性垫片调节定/动子间界面的预紧力。该装配结构能够保证电机动子具有2个方向的平面运动。

5 结论

1) 提出口齿形定子谐振驱动的平面电机，选定口齿形结构面外弯振、面内纵齿弯振、面外横齿弯振作为工作模态以驱动电机的平面运动。

2) 配置出定子压电极化供电模式，得到定子优化尺寸54 mm×45 mm×5.8 mm，设计出电机结构。

3) 建立定子的机电耦合分析模型并模拟出其纵、横齿驱动足的两相椭圆轨迹，验证了电机原理。

4) 正常激励时驱动足振幅可达微米级。当驱动电压为250 V时，驱动足沿x、y、z向振幅分别为2.1 μm、2.6 μm和2.0 μm。