行波型超声波电机等效电路建模

周先立，罗 萍，黄 龙，刘泽浪

(电子科技大学 电子薄膜与集成器件国家重点实验室，四川 成都 610054)

0 引言

行波型超声电机具有低速大力矩、运行平稳等特点，已广泛应用于机器人、仪器仪表、工业控制、精密定位和航天航空等领域。近10年，行波型超声波电机的研究发展始终围绕力矩、精度、稳定性和可靠性等性能提升的纵深方向发展,便需了解超声电机的振动及动力响应特性，建立准确的数学模型。目前超声电机数学模型[1-2]主要包括解析模型、等效电路模型和有限元建模。解析模型和有限元建模都存在求解复杂，使用不便等问题，等效电路模型在超声电机应用系统设计中更具适应性。在等效电路模型的研究方面，通过前人不断地完善超声电机等效电路模型，目前已有较成熟的超声电机定子模型，但未综合考虑电机压电耦合效应、定转子间的摩擦耦合情况及转子振动特性3方面的完整、准确的超声电机等效电路模型。

本文利用将受迫振动模型与电学模型类比推导的思想，提出了一种超声电机转子优化模型，建立了较完整的超声电机等效电路模型，并给出了模型中的参数计算方法。通过搭建实验平台验证了本模型能准确反映行波型超声波电机的电气特性，从而为进一步开展超声电机驱动器和控制器的设计提供了理论基础。

1 超声电机等效电路模型

基于超声电机机理，本文从定子、接触区域和转子3方面建立了超声电机等效电路模型。

1.1 定子模型

图1为国际上已有的、公认的超声电机压电定子的等效电路模型[3]。其中，Cd为定子的夹持电容，V、I分别为电机驱动电压、电流，电阻R、电感L、电容C分别为

L=Ms/A2

(1)

R=γs/A2

(2)

C=A2/ks

(3)

式中：Ms为定子含压电陶瓷和定子弹性体模态质量；A为力系数；γs为定子粘滞阻力系数；ks为定子模态刚度。

图1所示的模型描述了定子通过逆压电效应经阻抗Z的损耗后产生输出机械力F的过程。图中，v为机-电转换后的输出机械力输出速度，F为机电转换后的输出机械力。

图1 压电振子等效电路模型

1.2 接触区域模型

1.2.1 面接触、库仑摩擦模型

柔性转子在与定子行波接触时是一个接触面，并随着正压力增大而增大。超声波电机工作时，定子表面的轮廓线成正弦波形状。由于定、转子材料较硬，而预压力相对较小，故可假定定、转子本身不因此产生接触形变，只有摩擦层产生相应的形变，这就是刚性定子-弹性转子的面接触模型，如图2所示[4]。图中，ξ0为定子振幅，h0为定子厚度的一半。

图2 摩擦层的面接触物理模型

1.2.2 超声电机接触模型计算分析

面接触模型(见图2)反映了定子微观振动转换为转子宏观转动的过程。图2中接触边界x0处的纵向振动幅值为

us(0,x0)=ξ0coskx0

(4)

式中k=2π/λ为弹性波振动的波数。接触边界点：

x0=arccos(us/ξ0)/k

(5)

行波横向振动位移[5]为

ζ=kh0ξ0sin(kx-ωt)

(6)

对式(6)求导，令定、转子等速，有

kh0ξ0ωcoskx1=ωrotorr

(7)

式中ωrotor为转子角速度。式(7)化简可得定、转子等速点为

x1=arccos[ωrotorr/(kh0ξ0ω)]/k

(8)

式中：k为波系数；ξ0为定子0时刻波峰处的纵向振动幅值；r为平均接触半径；ω为角频率。

由图2可知，转子振幅ξ0(1-coskx0)为定子振幅ξ0的1-coskx0倍，所以，转子振动位移ur与定子振动位移us的关系为

ur=us(1-coskx0)

(9)

转子纵向的合力为定子行波波峰对转子的轴向压力Fsr，横向的合力为摩擦力FR。考虑到转子和摩擦材料的阻尼与摩擦层的等效刚度，转子的振动方程为

(10)

式中：Mr为转子质量；kf为摩擦材料等效刚度；γr为转子阻尼系数；γf为摩擦阻尼系数。

1.3 转子模型

将式(10)通过向量的方法化简后代入式(9)可得

FR+Fsr

(11)

将受迫振动与电学模型中的阻抗、容抗1/(jωC)、感抗jωL公式类比推导，得出的转子等效电路如图3所示。

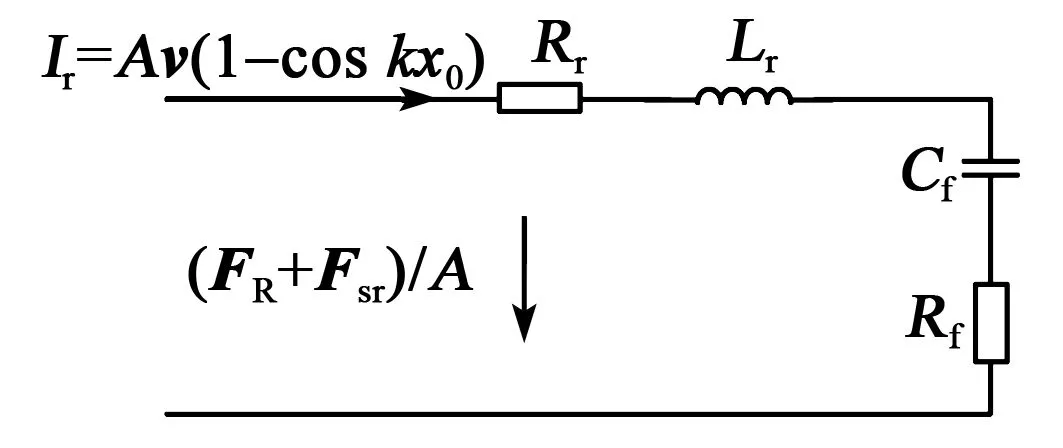
图3 转子侧等效电路

图3中，各个参数表达式为

Rr=γr/A2

(12)

Rf=γf/A2

(13)

Lr=Mr/A2

(14)

Cf=A2/kf

(15)

式中：Rr,Rf分别为受转子和摩擦阻尼影响后的电阻；Lr是转子质量为感性影响时的电感；Cf是摩擦材料刚度为容性影响时的电容。

添加支路与其并联进一步完善，图3的转子侧等效电路，新增的支路提供Avcoskx0大小的电流，使总电流Ir为Av，其中：

R′=(Rf+Rr)·m

(16)

L′=Lr·m

(17)

C′=Cf/m

(18)

m=(1-coskx0)/coskx0

(19)

完善后的转子侧等效电路如图4所示。

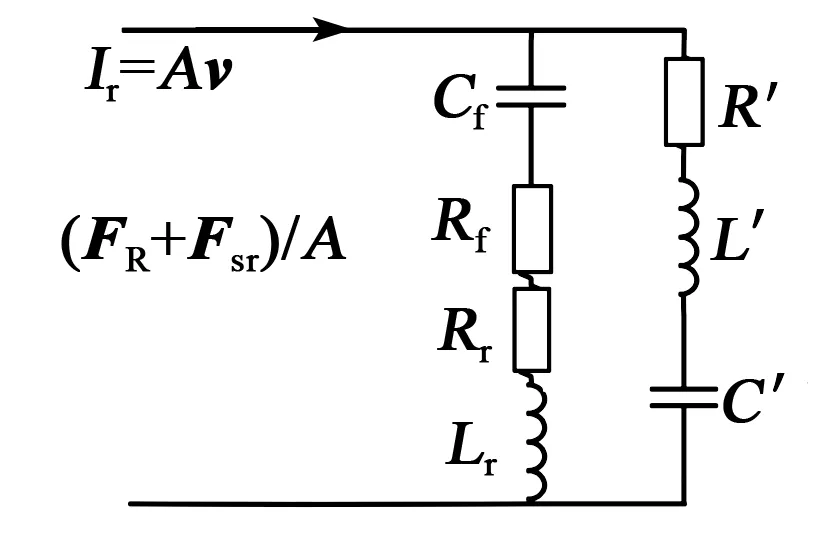
图4 优化后的转子侧等效电路

由图4与式(16)～(19)可看出，R′、L′、C′受m控制，m代表了电机的转动状态，因此，随着电机转动状态发生改变，可用图4中的R′、L′、C′这条支路来表征电机转动时阻抗的改变情况。由于在不同的转速下m值会改变，因此，图4的电机转子模型可反映转子对超声电机的整体性能带来的影响。

1.4 超声电机等效电路

综上所述，考虑到实际采用的是两相交变电源驱动，但由于A、B两相对超声电机的影响具有对称性，可视两相等效电路相同。因为定子对转子的输出机械力F就是转子在横、纵两方向受到的合力Fsr+FR，故可将定、转子模型结合，即将图1与图4合并，图5为两相之一的等效电路图。

图5 超声电机空载时等效电路

考虑到加负载情况下，转速比空载时低。由图2可看出，等速点x1、接触边界点x0会向下、向外移动，使整个接触区域变大，转子形变增大。通过转子侧等效电路的建模分析可知，转子侧等效电路总电流Ir=Av(1-coskx0)将增大，在原来图3基础上，支路电流增加表现为并联了RL支路，即可得超声电机负载时等效电路,如图6所示。图中V是由方波信号Vpulse经LLCC滤波网络后产生的超声电机输入信号。

图6 超声电机负载时等效电路

2 仿真验证

用HP4294A网络分析仪对行波型超声波电机样品进行测试，并合理选择驱动频率[6]，得到的实验参数如表1所示。

表1 参数测试数据

Cadence仿真中Cd=1.34 nF,Cf=75 pF,Vpulse=0～40 V,R=2.5 Ω,Rf=216 Ω,L=125.5 mH,Rr=5 Ω,C=9.5 nF,Lr=85.5 mH。R′、L′、C′值会随电机转动发生改变，在谐振频率下，一定转速时实测所得R′=4 338 Ω,L′=1.678 H,C′=3.82 pF。

空载时，基于图5的超声电机等效电路，采用LLCC滤波网络进行滤波[7]，搭建Cadence仿真平台，仿真如图7所示。

图7 超声电机等效电路的驱动信号仿真波形图

由图7可得到电机驱动电压52 V(峰-峰值)、电流32 mA(峰-峰值)且存在高次谐波的正弦信号。高次谐波存在的原因是LLCC滤波网络设计时未考虑波形的畸变率。

图8为超声电机有、无转子情况仿真的等效对比图。通过第1节的分析及图8的对比仿真结果可知，转子对整个电机模型的电气特性影响主要体现在转子质量Mr的感性特性与摩擦材料等效刚度kf的容性特性，而Mr与kf也是转子转动物理特性的关键设计参数，且电机在不同工作状态下，电机转速不同，将有不同的R′、L′、C′值，由于这种变化特性，使研究转子模型具有意义。

图8 超声电机有、无转子等效对比图

3 实验结果分析

对行波型超声波电机样机进行实测， 用H桥电路产生的0～40 V方波电压经LLCC谐振后得到的正弦驱动信号来驱动超声电机，超声电机能稳定转动，具有良好的动态特性。图9为驱动装置实物图。图10为超声电机其中一相的驱动电压、电流在有、无转子情况下的对比图，且与图8仿真对比图吻合。

图9 电机实验实物图

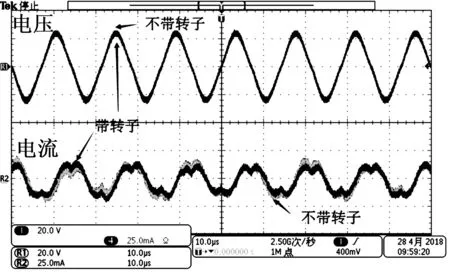
图10 超声电机驱动信号对比图

最终超声电机能正常转动，实测结果电机驱动电压V为50 V(峰-峰值)，驱动电流I为30 mA(峰-峰值)，且存在高次谐波信号，与理论分析一致，与仿真结果吻合，细微的差异是由于电机内部参数与选择的分离元件精度造成的。仿真与实验结果表明，得到的电流波形都含有高次谐波，这种非正弦特性正好充分验证了本文提出的超声电机转子优化模型与超声电机整体等效电路模型的准确性与完备性。

4 结束语

本文考虑电学的两相输入特性与电机物理模型横、纵向的差异性，推导出适合两相交流电输入的行波型超声电机等效电路模型；考虑摩擦耦合情况与转子对超声电机的影响，提出了摩擦层转子侧等效电路模型。对本文推导出的超声电机等效电路模型搭建了Cadence仿真平台,并进行了仿真验证。对样品电机搭建实验平台，测得实验结果，通过对比分析，验证了本文模型的准确性与完备性。本文建立的超声电机等效电路模型可为进一步开展超声电机的精准驱动和控制提供模型基础。