半圆形初始裂纹在交变拉伸载荷下的裂尖应力场数值模拟

周晓松，张焱冰，张岳林

1中国人民解放军军事科学院 国防科技创新研究院，北京100071

2海军工程大学 舰船与海洋学院，湖北武汉430033

3中国人民解放军91404部队，河北秦皇岛 066001

0 引 言

裂纹普遍存在于航空航天及海洋结构物中，例如，因材料缺陷和加工引起的初始裂纹以及疲劳载荷引起的萌生裂纹。因此，开展裂纹扩展规律及裂尖应力场的研究，对于准确评估板结构的剩余承载能力具有重要意义，尤其是对于承受交变波浪载荷的船体结构。为此，国内外学者开展了此类结构的极限强度研究。例如，Cui等［1］针对一系列不同长度、位置、方向角的裂纹，对钢板极限强度影响的非线性进行了有限元分析；Bayatfar等［2］对在单轴压缩载荷作用下的非加筋板和加筋板单元的极限强度特性进行了研究，发现裂纹长度及其位置对极限强度有着重要影响；闫小顺等［3］提出了一种坐标变换建模方法，用来解决球柱结合壳焊趾表面裂纹的有限元建模问题；吴建国等［4］基于能量差率基本原理，以非穿透裂纹深度的相对值作为控制裂纹虚比例扩展的无量纲几何参量，来构造求解裂纹张开位移幅值的伯努利微分方程，从而导出以裂纹绝对尺寸和相对尺寸为参数的裂纹张开位移幅值的表达式，得到了有限大体非穿透裂纹三维应力强度因子的闭合解。在上述研究中，大多数是将含裂纹的非加筋板或加筋板简化为二维薄壳结构，即认为裂纹厚度沿板截面是均匀分布的。然而，在实际工程应用中，裂纹在板截面上的形状往往是不规则的，故应用实体单元对裂纹扩展和裂尖应力场进行分析有望提高计算的精度。

本文将以半圆形三维初始裂纹为例，基于虚拟裂纹闭合技术（Virtual Crack Closure Technique，VCCT），运用Marc有限元程序，对裂纹在交变拉伸载荷作用下的裂尖应力场进行分析，从而为考虑初始裂纹的板结构疲劳强度计算提供参考。

1 Marc中的虚拟裂纹闭合技术

虚拟裂纹闭合技术最先由Rybicki和Kanninen［5］提出，主要用于计算二维裂纹的问题。该方法通过对有限元分析结果进行后处理，得到所需裂纹扩展的能量释放率。Shivakumar等［6］后来将该方法推广到了三维裂纹的计算中，Narayana等［7］则进一步发展了针对面状裂纹的一般形式的计算公式。在上述方法中，由于所需的断裂参数是对有限元分析结果进行后处理得到的，因此比较繁杂，也削弱了有限元分析和参数计算的有机联系。为此，Xie和 Biggers［8］提出了哑节点断裂单元（Fracture element with dummy nodes）方法。图1所示为一个九节点块体单元的虚拟裂纹闭合法示意图［4］。图中：只有位于裂纹尖端的节点1和2对单元的刚度矩阵产生影响；节点3和4用于计算裂纹张开位移；节点5～9用于确定局部坐标系并计算虚拟裂纹的扩展面积。为计算裂纹尖端处的节点力，在节点1和2之间放置刚度很大的强弹簧。

图1 九节点块体单元的虚拟裂纹闭合法示意图［4］Fig.1 Sketch of 9-node solid elements using VCCT［4］

由此，可得到3种断裂形式的应变能释放率，分别表示如下：

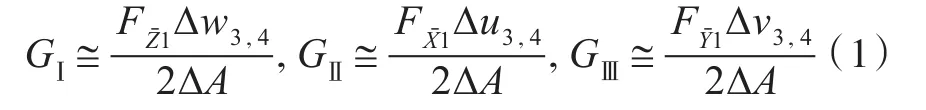
式中：GⅠ，GⅡ和GⅢ分别为3种断裂形式的应变能释放率；为由全局坐标系转换为局部坐标后节点 1上的节点力；Δu3，4，Δv3，4和Δw3，4为局部坐标下节点3和4之间的相对位移；A为裂纹深度。

对于复合型断裂，当断裂判据满足式（2）时，

此时，节点1和节点2处的强弹簧完全失效，裂纹扩展。其中，GⅠC，GⅡC和GⅢC分别为3种断裂形式应变能释放率的门槛值。

2 裂纹扩展的数值模拟

2.1 模型概述

图2所示为本文构建的数值模型。具体尺寸及相关参数如下：板尺寸为200 mm×100 mm×20 mm，单元数划分为26 660个，节点为4 743个，裂纹半径为5 mm。材料为DQSK36，材料密度为7.85×10-9t/mm3，杨氏模量为2.07×105MPa，泊松比为0.28。图3所示为DQSK36材料的塑性力学特性曲线。本文模型采取左侧固支，右侧施加随时间t变化的载荷P，并由下式计算：

图2 模型网格划分Fig.2 Meshing of the model

图3 DQSK36材料塑性力学特性Fig.3 Plasticity mechanical characteristics of material DQSK36

2.2 初始裂纹定义

本文将模型视为接触体，并基于VCCT方法指定在疲劳加载模式下裂纹扩展的相关参数。其中，疲劳载荷周期取为1 s，裂纹扩展增量取为4 mm，裂纹扩展方向采用最大Hoopstress方法。

在构建初始裂纹尖端和裂纹扩展尖端周围的网格时，采用全局网格重划分技术自动完成，并使用了Patran四面体网格生成器。通过距离控制单元尺寸的变化，在距离裂纹尖端20 mm以内的区域，对网格进行细化，接近裂纹尖端部位采用单元长度为3 mm的网格重新划分，逐渐远离裂纹尖端时采用过渡网格，其他部位采用均匀的10 mm单元尺寸划分。

采用Crack initators定义初始裂纹尖端自动建模的参数，通过小面构成的曲面在接触体中插入模板裂纹。然后，分别定义预载荷和往复加载分析工况，其中预载荷工况采用1个增量步，在0.5 s内完成；往复加载工况采用10个增量步，在5 s内完成，激活全局网格重划分和初始裂纹建模选项，提交计算。

3 裂纹水平面的应力场

打开Marc有限元程序的结果后处理文件，读取计算结果，得到如图4所示的裂纹水平面的应力云图。由图可以看出，由于模型的对称性，裂尖应力场关于裂纹中心点对称分布。

图4 裂纹水平面的应力云图Fig.4 Stress contours of crack in horizontal plane

图5所示为以下面的裂尖为原点，在极坐标系下，在不同时刻（t=1.5，2 s）时的von Mises等效应力随r的变化曲线。图中，r为计算点离开裂纹尖端的距离，a为裂纹长度，θ为裂纹与载荷方向的夹角。

当t=1.5 s时，在θ=0或 π位置，计算点的von Mises等效应力随着离开裂尖距离的增大而呈线性增大，当r=0.08a时达到最大值，为155 MPa，此时的载荷为100 MPa。用该值无量纲化计算的点应力为1.55P，此后计算点的von Mises等效应力随离开裂尖距离的增大而呈线性减小。

当t=2 s时，载荷由100 MPa降低到50 MPa，降幅达 50%。在θ=0，π，π/6，5π/6，-π/6，-5π/6，-π/3，-2π/3，-π/2 位置，随着载荷的减小，计算点的von Mises等效应力比t=1.5 s时刻的有所减小，但幅度小于载荷减小的幅度（50%）。这说明计算点发生了塑性变形，计算点的von Mises等效应力随r的变化规律与t=1.5 s时刻的相似，即基本上呈线性或双线性关系。而在θ=π/3，2π/3，π/2位置，在载荷变小的情况下，当0≤r＜0.35a时，von Mises等效应力随r的增大而迅速减小，当r=0.35a时达到最小。这是因为在整个加载过程中r=0.35a附近区域的von Mises等效应力水平均未超过材料的屈服应力，其未发生塑性应变。

图5 不同时刻von Mises等效应力随r的变化Fig.5 Variation of von Mises equivalent stress with r at different times

4 裂纹横断面的应力场

图6为在不同时刻裂纹横断面的应力云图。由图可以看出，在裂纹横断面上，裂纹的扩展方向总是沿着裂纹形状的法向，即以裂纹中心为原点，在极坐标下，a为任意值时计算点的von Mises等效应力随r的变化均一致。由此，本文绘制了任意a位置时的裂纹横断面应力随r变化的曲线，分别如图7和图8所示。

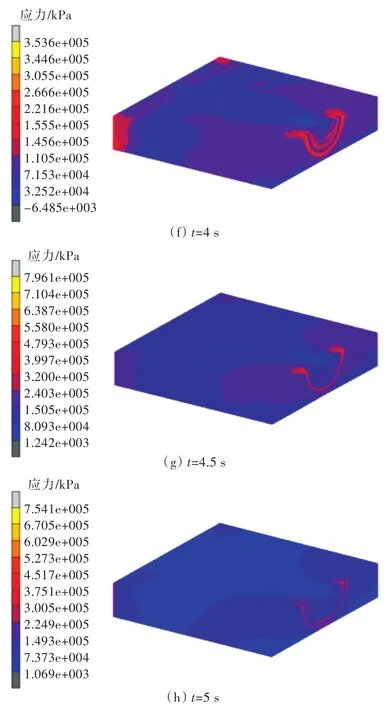
图6 裂纹横断面不同时刻的应力云图Fig.6 Stress contours of crack cross-section at different times

图7 不同时刻裂纹横断面应力随r的变化曲线Fig.7 Variation of crack stress in cross section with r at different times

图8 不同时刻裂纹横断面应力随r的变化曲线Fig.8 Variation of stress at crack cross section with r at different times

当t=1.5 s时，计算点的von Mises等效应力随r的增大而增大，在r=0.5a时达到最大，此位置恰好在裂纹边缘，其应力值为1.45P。此后，von Mises等效应力随r的增大而减小，当r=0.8a时，von Mises等效应力-r/a曲线逐渐呈平稳的直线，应力值趋向于P，即距原点的距离大于0.8a的位置不再产生应力集中。

当t=2 s时，计算点的von Mises等效应力随r的增大先增后减，在r=0.9a时达到峰值2P。此后，von Mises等效应力随r的增大而减小，在r=1.4a时，应力值趋向于P。

对于t=2.5s时的情况，当r＜0.9a时，计算点的von Mises等效应力随r的变化仍然呈现出高度非线性，在r=0.9a时，von Mises等效应力达到峰值2P，此后，von Mises等效应力随r的增大而减小；在r=1.5a时，von Mises等效应力值趋向于P。

综上所述并结合图8，得出了如表1所示的不同时刻von Mises等效应力出现的位置（瞬时裂纹半径rt）、应力集中开始消失的位置rd以及裂纹边缘应力峰值σmax。其中，比值rd/rt表示裂纹位置的严重程度，值越大，应力集中越严重。

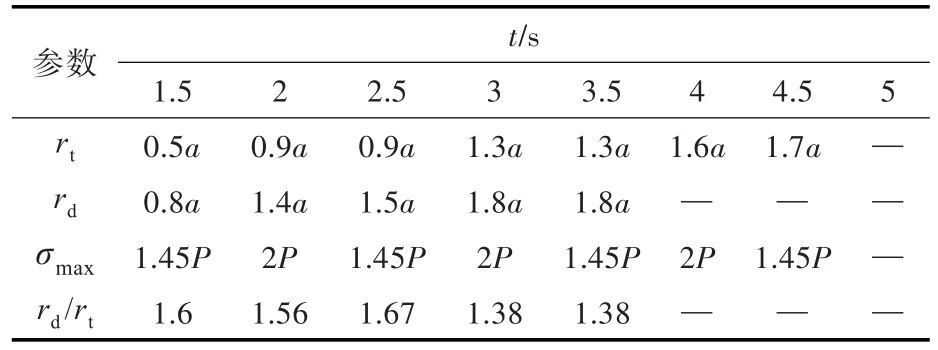
表1 裂纹横断面应力场参数随时间变化Table 1 Parameters of the stress field in cross section of crack varying with different times

由表1可知：在任意时刻下，应力集中总是从1.38～1.67倍裂纹半径的位置开始消失；当载荷为2/3倍材料屈服应力时，裂纹边缘应力峰值总是等于1.45P；当载荷为1/3倍材料屈服应力时，裂纹边缘应力峰值总是等于2P。

需要指出的是，由于在t=4 s后裂纹扩展到板厚近末端，故整个模型中不再出现应力集中消失的位置，尤其是在t=5 s时，结合图6中t=5 s时的裂纹横断面不同时刻的应力云图，裂纹扩展到板厚边缘贯穿了整个板厚。

5 结 论

本文基于三维虚拟裂纹闭合技术，以半圆形初始裂纹为例，研究了其在交变载荷作用下的裂尖应力场。根据本文的研究，得到以下结论：

1）对于裂纹水平面的应力场，在发生塑性变形的区域，其von Mises等效应力随计算点距裂尖距离的增大而减小，两者之间基本上呈线性或双线性关系；在未发生塑性变形的区域，基本上是裂尖距离的三次函数。

2）对于裂纹横断面，裂纹总是沿裂纹边缘形状的法向方向扩展，应力最大值总是出现在裂纹边缘。在裂纹内部，应力值随着距裂纹中心的距离而呈现高度的非线性分布；在裂纹外部，应力值随着距裂纹中心距离的增大而减小。当距裂纹中心的距离大于裂纹半径1.67倍时，应力集中消失。

3）同样，对于裂纹横断面，当载荷为材料屈服应力的2/3倍时，裂纹边缘最大应力值总是为载荷的1.45倍；当载荷为材料屈服应力的1/3倍时，裂纹边缘最大应力值总是为载荷的2倍。