基于动态性能空间理论的运算放大器正相反馈控制器设计

陈旭东

(安徽新闻出版职业技术学院 机电信息系，安徽 合肥 230601)

相同零、极点在根轨迹平面的不同位置表现出不同的动态性能，表明系统动态性能与零点或极点本身无关，完全由其所处的位置决定[1]。基于此，文献[1]借助数理分析中的“场论”概念[2]，认为无论零、极点是否真实存在，根轨迹平面的每一个位置点，都对应着一组确定的控制性能值，可表示为：

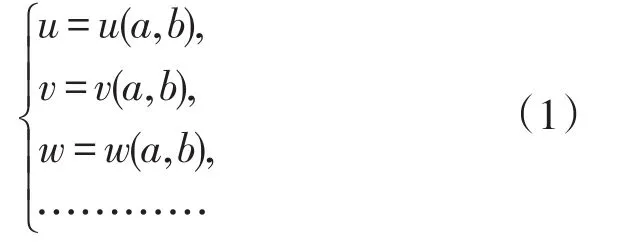
其中(a,b)为零、极点的根轨迹坐标，（u,v,w,…）为系统的一组性能指标[1]。

文献[3-4]系统研究了控制系统的动态性能，已得出以下结论：

1）频率特性曲线中工作频段带宽频率ωb的大小决定了定位精度的高低，ωb越大系统定位时间越短，定位精度越高；

2）幅频特性曲线中第一个谐振峰的峰值Mr大小决定了控制稳定性的高低。Mr越大系统相频特性曲线下穿-180°处的斜率越大，控制稳定性越低。

在此基础上，文献[5]选取定位精度ωb和控制稳定性Mr作为系统动态性能的描述量，构建了极点根轨迹坐标(a,b)与系统性能指标(ωb,Mr)之间的函数对应关系，并分别以b=±a和b=0作为分界线，将根轨迹平面划分为动态系能配置区、不可观测区和实数极点配置区三个子空间：

①动态系能配置区(复共轭极点且当|b|＞|a|时)：

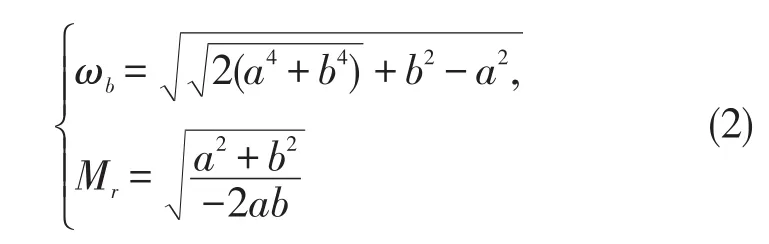
②不可观测区(复共轭极点当|b|≤|a|，且b≠0时)：

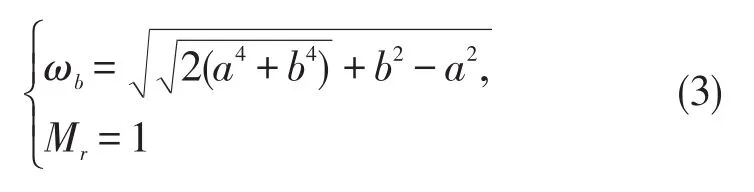
③实数极点配置区(实数极点当b=0时)：

依据公式(2)～(4)，通过选取不同的ωb和Mr值，采用在根轨迹平面绘制一系列等ωb线和等Mr线的方法构建了系统的动态性能空间[5]。

本文尝试应用该动态性能空间理论，对运算放大器正相反馈控制器结构及参数的优化设计方法予以研究。

1 正相运算放大器闭环系统

1.1 运算放大器的电路结构

运算放大器(operational amplifier，Op-Amp)电路结构示意图如图1[6]。若以Vp和Vm分别表示放大器正、负极的输入电压，则输出电压V0和输入电流Iin可表示为：

式中，A为放大器开环直流增益，一般介于105～107之间，大小由图1中电压控制电压源的多项式系数确定；Rin，Rout分别是放大器的输入和输出电阻。

因通常情况下，Op-Amp中Rin远大于Rout[7]，故输入电流Im和输出压降IoutRout可近似认为趋于0，则(5)式简化为：

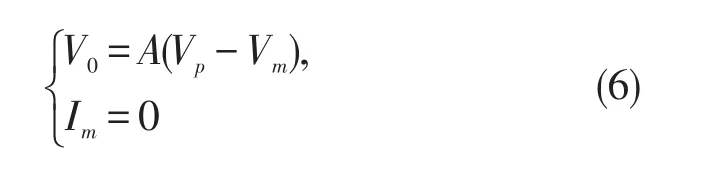
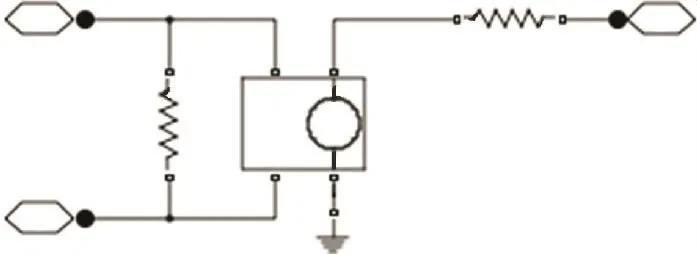
图1 运算放大器电路模型

本文以Texas instrument公司OPA1678型运算放大器为研究对象，将参数值：A=105，Rin=106Ω和Rout=100 Ω[8]代入式(6)，并将因系统参数及外界温度变化而产生的不确定性作为低频扰动信号，而将位于工作频段外其它可能存在的极点影响作为高频环境噪声；同时设定该运算放大器工作于非饱和状态的线性模式；则可求得Op-Amp传递函数如式(7)：

由(7)式知，Op-Amp开环系统为两个实数极点构成的稳定系统，依据动态性能空间理论，其动态性能应主要由主导实数极点z1=-104决定，经由公式(4)求解，得到系统定位精度和控制稳定性指标分别为：

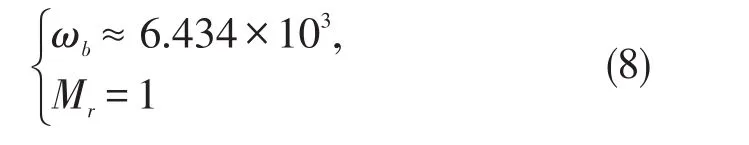
图2 运算放大器开环伯德图及阶跃响应曲线

绘制Op-Amp开环伯德图如图2(a)和阶跃响应曲线见图2(b)。可见，系统带宽ωb≈6.5×103rad·s-1，定位时间 t≈5×10-4s，显示定位精度较高；频率特性曲线和阶跃响应曲线中均未出现明显振荡，表明稳定性较强。实验结果与式(8)计算结果一致。

1.2 远算放大器正相并联电阻反馈控制器

为增大Op-Amp带宽，选取电阻R1和R2构建正相并联电阻反馈控制器Kb1如图3。其中图3(a)为电路结构，图3(b)为闭环系统控制结构示意图。

由图3(a)可求得控制器Kb1传递函数

则Op-Amp闭环系统传递函数为

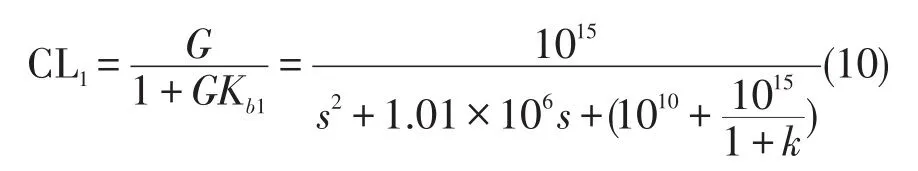
求出CL1中复共轭极点的实部和虚部

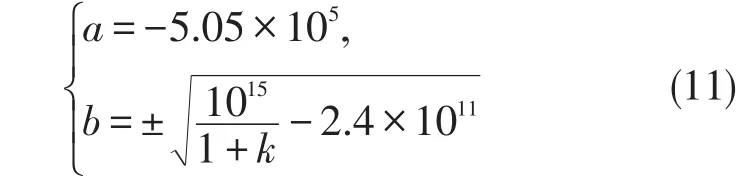
由(11)式知，随着偏置电阻比值的减小，复共轭极点实部不变而虚部增大，依据动态性能空间理论，系统带宽将随之增大，而控制稳定性降低。

图3 运算放大器电阻并联反馈网络结构

求解系统闭环直流增益A0

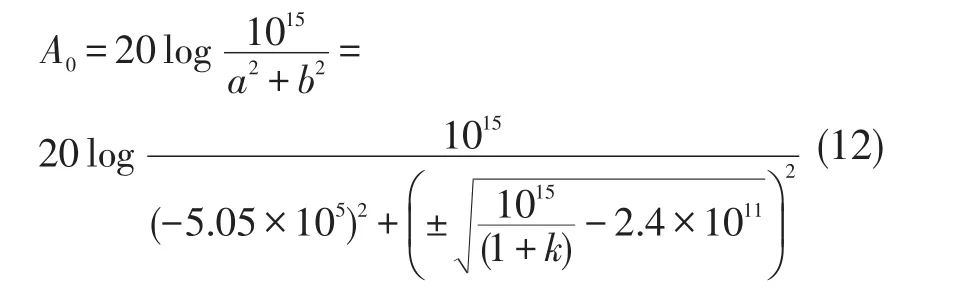
可见A0随k值的减小而降低。

综合上述分析，得到如下推论：

1)若k→∞，即R1=0 且，则 CL1与G传递函数表达式一致，表明该Op-Amp闭环系统的最低带宽为ωb≈6 434 rad·s-1，最高直流增益A约为100 dB。

2）当k减小至4 166时，复共轭极点的虚部恰好不为0，表明在∞＞k≥4 166倍率范围内，极点工作于实数极点配置区，闭环系统保持最高的控制稳定性(Mr=1)，较低的带宽和较高的直流增益，依据公式(4)及式(12)，可求得带宽范围为[6 434,3.25×105]，而直流增益则满足 100≥A0≥71.87。

3）当k减至2 019时，复共轭极点的虚部|b|增大至恰与实部|a|相等，表明 4 166＞k≥2 019 条件下，极点位于不可观测区，Op-Amp闭环系统仍应保持最高的控制稳定性(Mr=1)，带宽范围增大至(3.25×105，7.14×105]，直流增益则介于(65.85,71.87)之间。

4)随着k取值的进一步减小，复共轭极点进入动态性能配置区，Op-Amp闭环系统的带宽继续增大，但控制稳定性和直流增益则随之降低。

5）当k=0(R1≠0 而R2为 0)时，复共轭极点的虚部|b|取得最大值，闭环系统此时具有最大的带宽(ωb≈4.913×107rad·s-1)、最低的控制稳定性(Mr约等于5.596)和最小的直流增益(A=0)。

为验证上述推断，分别取k1=0，k2=9，k3=2019，k4=4 166 和k5→∞，代入公式(2)、(3)和(4)求解动态性能指标，结果如表1所示，并做伯德图和归一化阶跃响应曲线如图4，为便于比较，图4中同时绘制了开环系统G的特性曲线。

图4可见，当k→∞时，闭环系统伯德图和阶跃响应曲线完全与G重合，带宽频率ωbmin≈6 400 rad·s-1，直流增益达到最大值约为100 dB，表明无论采用何种反馈网络作为控制器，均不可能降低原有运算放大器的带宽和增大其增益；随着k值的逐渐减小，带宽频率增大而直流增益降低，当k直至减小到2 019时(对应的带宽增加至约7.14×105rad·s-1，直流增益降为A0≈65.85 dB)，闭环系统仍保持相当的稳定性；但注意到：CL(k4)与CL(k3)比较，虽然伯德图幅频特性曲线中振荡峰高度始终相等保持Mr=1，但相频特性曲线在下穿-90°相位处斜率发生了变化，由CL(k4)的-20 dB/dec(一阶惯性环节下降斜率)增加为CL(k3)的-40 dB/dec(二阶振荡环节下降斜率)，表明系统的构成由实数极点向复共轭极点发生了转化[9]；同时图4(b)也显示CL(k3)阶跃响应曲线中出现了微小的振荡；随着k值的进一步减小，闭环系统带宽持续增加，但幅频特性曲线出现了明显的振荡尖峰，对应于阶跃响应曲线的振荡加剧，k2=9时系统带宽约为1.55×107rad·s-1，直流增益降低为A0=20 dB；当k1取值为0时，Op-Amp闭环系统达到最大带宽ωbmin≈4.913×107rad·s-1，直流增益则降为最低值A0≈ 0。

2 运算放大器正相RC反馈控制器设计

表1 不同电阻比值条件下的闭环系统动态性能指标

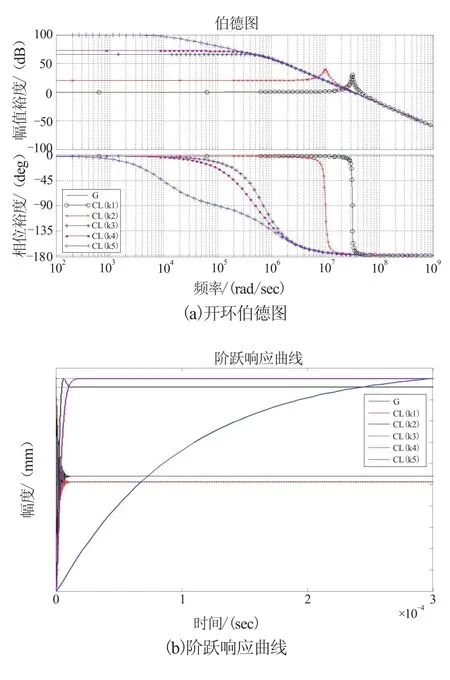
图4 电阻并联网络运算放大器闭环伯德图及阶跃响应曲线

2.1 复共轭极点优化配置点

若采用并联电阻正相反馈控制器，因传递函数中仅k=R2/R1唯一可调，无法在增加ωb的同时降低Mr，导致系统带宽频率仅增加至7.14×105rad·s-1(约11.1倍于开环带宽频率)时，系统即发生了振荡。为在增加带宽频率的条件下提升系统控制稳定性，引入电容器C作为另一可调参数，构建电路结构如图5所示的正相RC反馈控制器Kb2，控制结构示意图仍采用图3(b)。

由图(5)可求得Kb2具有如下传递函数形式

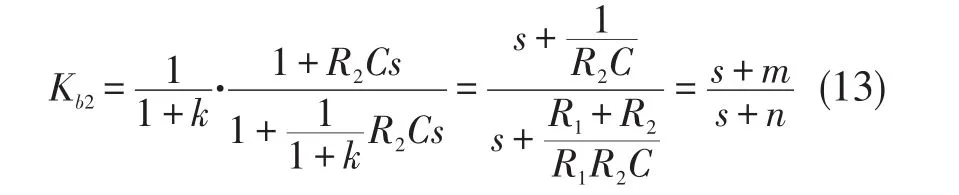
其中实数零、极点m、n分别为：

图5 RC反馈网络运算放大器闭环结构

并得到由一个实数零点、一个实数极点和一对复共轭极点构成的3阶Op-Amp闭环系统CL2

选取k2=9时的带宽频率1.55×107rad·s-1为设计目标带宽ωb。若综合考虑系统动态性能的提升和对高、低频扰动信号的抑制效果，则Op-Amp闭环系统中实数零点、实数极点及复共轭极点的优化配置范围界定如下：

1）复共轭极点的优化配置范围

为使闭环系统的带宽等于设计目标带宽，CL2中复共轭极点的定位精度应等于1.55×107rad·s-1；同时为提升系统控制稳定性，其Mr值应等于1。为此，在动态性能空间中过ωb=1.55×107rad·s-1做等精度线，并做b=±a等振荡线如图6所示。可见，满足上述最优配置条件的复共轭极点应位于不可观测区内的那部分等精度线上。为便于比较，从等精度线与等振荡线b=±a的交点X点出发，沿实部|a|增大方向随机选取X(-1.1×107，±1.1×107)、Y(-1.7×107，±1.0×107)和Z(-2.3×107，±4.5×106)三个点作为目标配置点。

2）实数极点的优化配置点

对于实数极点P，若其定位精度ωbP小于设计带宽，由动态性能空间理论知，系统带宽将改由该实数极点确定，无法实现设计要求；反之若ωbP大于ωb，则ωb＜ω＜ωbP的高频范围内，幅频特性曲线将以单对复共轭极点所产生的-40 dB/dec斜率下降，小于ωbP频率外复共轭极点与实数极点共同作用下的-60 dB/dec下降斜率，闭环系统对高频环境噪声抑制效果将减弱。因此实数极点定位精度也应当与设定目标频率相等，对应的根轨迹坐标为P(-2.41×107,0)。

图6 动态性能空间

3）实数零点的优化配置点

为提高直流增益，并增加系统对高、低频扰动信号的抑制效果，实数零点Z的取值应尽可能远大于实数极点P[11]。

4)应保持直流增益A0=20 dB不变。

选取上述P点作为实数极点，X、Y和Z分别为复共轭极点，做闭环系统传递函数CLX、CLY和CLZ为：

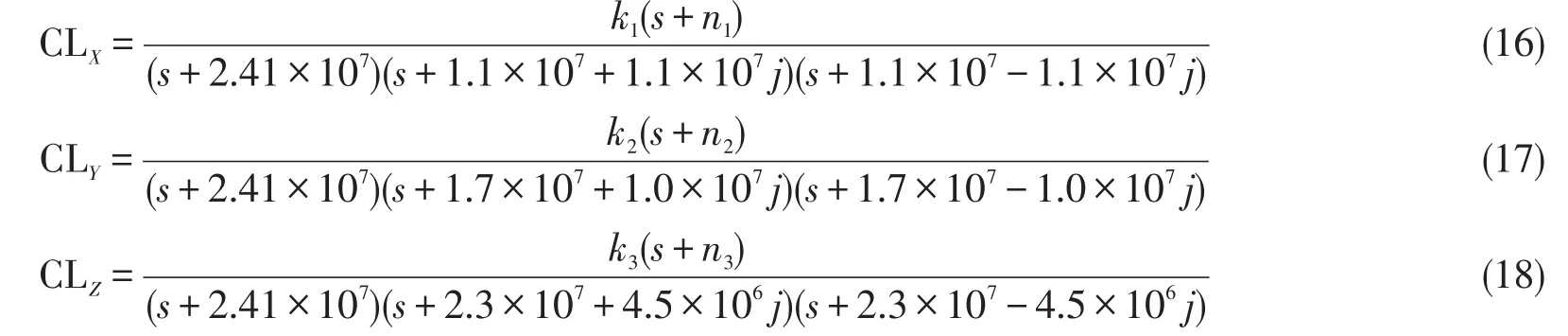
将式(16)～(18)分别与(15)式联立，并令电阻R2=90 kΩ，计算结果如表2所示。

表2 不同复共轭极点条件下RC反馈网络电阻和电容参数及控制器传递函数

Op-Amp闭环系统传递函数为：绘制并联电阻反馈控制器闭环系统CL(k2)(复共轭极点(-5.05×105，±1×107)也位于等精度线ωb=1.55×107rad·s-1上)，RC 反馈控制器闭环系统 CLX、CLY和CLZ的伯德图及阶跃响应曲线如图7所示。为便于比较，图7(a)中也绘制了Op-Amp开环系统G的频率响应曲线。图7可见，若保持实数极点位置不变，而将复共轭极点沿ωb=1.55×107rad·s-1等精度线向实部|a|增大的方向移动时：1）闭环系统控制稳定性显著提升，且当复共轭极点进入不可观测区间后，Mr保持最小值1基本不变；2）闭环系统带宽保持约ωb=1.55×107rad·s-1基本不变，但随着振荡幅度的逐渐降低，阶跃信号定位时间满足关系式：tZ(3.2×10-7s)≤tY(4.8×10-7s)≤tX(8×10-7s)≈5%tk2(1.4×10-7s)。3)直流增益降低明显，由原CL(k2)的20 dB依次降低为CLX的18.6 dB、CLY的 15.4 dB 和 CLZ的 12.8 dB。

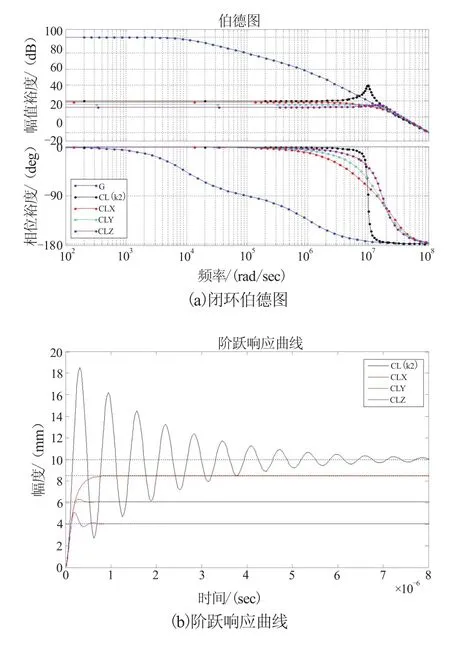
图7 CL(k2)、CLX、CLY和 CLZ系统闭环伯德图及阶跃响应曲线

图8显示 CL(k2)、CLX、CLY和 CLZ的灵敏度函数S和补灵敏度函数T的结果。图中可见，比较于 CL(k2)，CLX、CLY和 CLZ在设定目标频率 1.55×107rad·s-1附近的振荡尖峰明显消失，表明这3个系统均具有良好的鲁棒稳定性；图8(a)灵敏度函数中可见，直流增益ACLZ=-88 dB＜ACLY=-85 dB＜ACLX=-82 dB＜ACL(k2)=-80 dB，表明 CLZ对低频扰动信号具有最好的抑制效果[11]；而补灵敏度函数则显示在高频段4者具有基本相同的下降斜率，表明对高频环境噪声的抑制效果大致相同[12]。因此，当将复共轭极点配置至目标等精度线ωb与等振荡线b=±a的交点X时，Op-Amp闭环系统具有较好的动态性能、鲁棒稳定性以及较强的抗干扰能力；但系统直流增益A0仍然降低了约1.4 dB。

2.2 实数极点优化配置点

由公式(14)和(15)知，若采用RC反馈网络闭环系统，因控制器中仅有电阻比值k及电容C可调，这可能会导致实数零点、实数极点和复共轭极点之间仍然存在关联性，即无法在保持实数极点和复共轭极点位置不变的条件下，通过单独增大实数零点坐标的方法提升系统的直流增益。同时由式(19)发现：当运用动态性能空间理论采用待定系数法求解控制器传递函数时，闭环系统中实数极点与初始设定值之间发生了少量“偏移”，且该偏移并未造成系统动态性能、鲁棒性能和抗干扰能力的显著降低。因此，为提升系统的直流增益，尝试在保持复共轭极点不变的条件下，进一步对实数极点予以修正。

图8 CLX、CLY和CLZ系统灵敏度和补灵敏度函数

以 2.1 节中X点(-1.1×107，±1.1×107)作为复共轭极点的配置点，在式(18)原实数极点P(-6.81×106,0)两侧分别取P1(-4.8×106,0)、P2(-5.8×106,0)和P3(-7.8×106,0)、P4(-8.8×106,0)各 2 个点，由上述方法求解控制器表达式及电阻、电容参数值列表如表3所示。可见，随着实数极点根轨迹坐标的减小，m、n比值由KP4的 0.146，依次减小为0.133、0.118、0.102，直至KP1的 0.08，表明控制器中实数零点m的变化幅度大于实数极点n。由(12)式可知，该比值的减小将导致系统直流增益逐渐升高。绘制 CL(P1)、CL(P2)、CLX、CL(P3)及 CL(P4)的伯德图和阶跃响应曲线如图9。可见，经将式(19)中CLX的实数极点由P点(-6.8×106,0)分别配置至P2(-5.8×106,0)和P1(-4.8×106,0)后，闭环系统直流增益由18.6 dB增加至19.9 dB和21.2 dB，而控制稳定性和带宽基本保持不变。同时，阶跃信号定位时间由原CLX的0.8×10-6s，增加到CL(P2)的 1.2×10-6s和 CL(P1)的 1.4×10-6s，显示系统定位精度略有降低但控制稳定性不变。

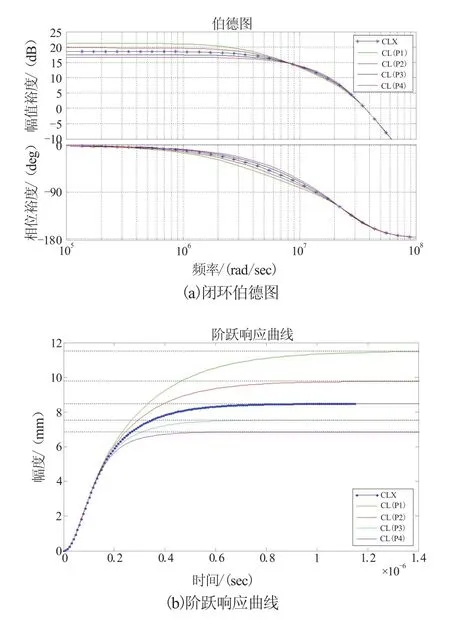
图9 CL(P1)、CL(P2)、CLX、CL(P3)及 CL(P4)系统闭环伯德图及阶跃响应曲线

3 小结

本文基于动态性能空间理论，对Op-Amp正相反馈控制器进行了研究。发现：若控制器采用正相并联电阻反馈网络形式，则所构建闭环系统中仅有电阻比值k=R2/R1唯一可调，且当带宽增加至ωb≈7.14×105rad·s-1(约为开环带宽的 11.1 倍)时，系统即发生了振荡。为了在增加带宽的前提下提升系统控制稳定性，引入电容C作为另一可调参数构建了正相RC反馈控制器，并在设定带宽频率ωb=1.55×107rad·s-1条件下，对控制器参数进行了最优化求解，结果显示：当控制器实数极点位于约(-3.7×106)，复共轭极点位于等ωb精度线与等b=±a振荡线的交点(-1.1×107，±1.1×107)，即电容C=2.47 pF，电阻R1=1.02 kΩ 和R2=90 kΩ 时，Op-Amp闭环系统的直流增益为19.9 dB、带宽达到约 1.55×107rad·s-1、控制稳定性Mr≈1，具有较好的动态性能和最强的抗干扰能力。

表3 不同实数极点条件下RC反馈网络电阻和电容参数及控制器传递函数

同时我们也发现，系统动态性能和抗干扰能力的增加可能降低其直流增益，原因在于采用正相RC反馈控制器时，Op-Amp闭环系统的实数零、极点仍不具有独立可调性。而该直流增益的降低可能导致系统鲁棒性能的下降，为此，需要对所设计RC反馈控制器中的实数极点予以微调，通过局部降低系统动态性能的方法以补偿其直流增益的减小。如何在k、C基础上，引入第三个可调参数，实现Op-Amp正相反馈系统等的最优化控制设计将是我们今后研究的重点。