基于SVM的食双星光变曲线自动分类算法*
袁慧宇,赵 娟,戴海峰,杨远贵
(1. 淮北师范大学信息学院,安徽 淮北 235000;2. 淮北师范大学,安徽 淮北 235000)
在信息与计算技术等新兴科技的驱动下,天文研究领域已从传统的单目标观测和手工处理数据转向多目标观测和自动数据处理[1]。大量巡天项目的开展为天文学研究提供了海量数据,如ROTSE,ASAS,SuperWASP,MACHO,OGLE,SDSS,LAMOST和Kepler等,由计算机自动完成目标交叉证认[2]、观测、实时数据处理和分析[3]等,获得光谱、测光、周期以及类型等数据。随着数据量的进一步增大,单服务器难以实时完成数据处理,分布式计算被应用到数据处理中提高处理效率[4]。面对海量天文数据,必须借助支持向量机、神经网络、遗传算法等人工智能算法对数据进行分析和处理,挖掘有用的信息[5]。例如:基于随机森林方法对SDSS和XMM数据的天体进行分类[6];基于机器学习方法寻找射电脉冲信号[7];基于密近双星的Roche势对双星进行分类[8]等,这些标志着天文学研究迈入了大数据时代。
通过观测获得的食双星光变曲线,可以快速确定其类型,搜寻出具有特殊演化意义的双星系统,为研究一些特殊天体和现象提供了重要的研究窗口。这对丰富和发展双星的研究内容,通过食双星认识星团和星系的形成和演化具有重要的意义。文[9]使用多项式拟合光变曲线,根据拟合后曲线的主极小和次极小的宽度和深度给出光变曲线类型;文[10-11]使用傅里叶变换提取光变曲线数据的频率特征,根据所得频率特征进行分类,但在算法实现上使用了软件计算的完美光变曲线数据进行参数设置,使用特征量较少,未考虑仪器测试误差、天气原因等引起的数据波动影响,因此仅能完成对光变曲线进行初步分类,不能识别载有特殊天文现象的光变曲线。
本文提出一种基于支持向量机(Support Vector Machine, SVM)的食双星光变曲线自动分类算法,以快速傅里叶变换所得的频率信号为特征量,对支持向量机模型进行训练获得能自动分类的模型。
1 自动分类算法
食双星光变曲线可分为EA,EB和EW 3种,针对分类需求提出分类方法如图1。第1步对原始数据进行预处理,归一化原始数据并减小其中噪声;第2步通过快速傅里叶变换提取频率信号作为特征数据;第3步使用支持向量机算法训练分类模型并测试;第4步对流程优化,获得最优的分类模型。
1.1 数据预处理
自动化全天巡视(All Sky Automated Survey, ASAS)用理论光变曲线所得特征进行分类,未考虑实测数据中的噪声影响[12]。而本文使用食双星目录与图集[注]http://caleb.eastern.edu(Catalog and AtLas of Eclipsing Binaries, CALEB)实测数据(包括相位和较差星等)。由于天气因素以及仪器误差等影响,实测数据不可避免地带有噪声影响。为了降低噪声的影响,首先进行预处理。
(1)归一化,相位数值在[0, 1]之间,不需要处理。较差星等可通过(1)式归一化到[0, 1]之间。
(1)
其中,m′为归一化后的较差星等;m为原始较差星等;mmax和mmin分别为较差星等最大值和最小值。
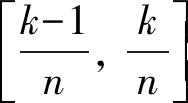

图1 光变曲线分类方法
Fig.1 Automatic classification algorithm scheme for light curve
(2)
(3)
1.2 光变曲线特征提取
原始光变曲线为时间序列数据,需将其特征提取出来用于分析。常用特征包括主极小和次极小差值、主极小波谷半高全宽等。本文采用光变曲线的频率特性作为特征值。实际实现时可用快速离散傅里叶变换将相位/较差星等变为频域信号,将频域信号与对应光变曲线类型组成特征数据集{f0,f1, ...,fd,T},其中fi(i=0, 1, ...,d)为频率分量,T为光变曲线类型。
1.3 支持向量机分类算法
支持向量机是建立在统计学习理论和结构风险最小原理基础上的一种有监督的机器学习算法,基本思想是将特征值映射到高维向量空间,获得可将不同类数据分割的超平面,该算法常作为自动分类的机器学习算法。在实际使用中,通常将原始数据分为训练集和测试集。使用训练集训练支持向量机模型,获得映射函数和分割平面(即分类模型),使用测试集验证所得模型。
2 实验与结果分析
算法实现采用Python编程。Python是一种面向对象的解释型计算机编程语言,由于其易用性、简洁性和可扩展性,成为最受欢迎的程序设计语言之一。Python拥有大量的科学计算扩展库,可用于实现本文提出的算法。
2.1 分类实验实现
第1步进行原始数据下载和收集。本文使用Urllib3和BeautifulSoup库自动分析CALEB网页数据并存储网站提供的300个变星的坐标、星名、类型及747条光变曲线,但网站未给出光变曲线类型。随后通过变星坐标与变星总表[注]http://www.sai.msu.su/gcvs/gcvs/intr.htm(General Catalogue of Variable Stars new version, GCVS)数据交叉对比获得光变曲线类型。
第2步实现光变曲线数据预处理。这里以BE Vul(EA),YY Cet(EB)和TW Cet(EW)3个变星的V波段数据为例。原始数据如图2(a)。由图2(a)可知,由于观测设备等限制,观测数据质量较差。表现为数据点个数不一致、浮动较大、数据较离散等。将相位均分为间隔0.005的新相位点,应用归一化/均值滤波/线性插值后所得数据如图2(b)。由图2(b)可知,预处理保留了原始数据的变化趋势,相对原始数据更加平滑。

图2 原始数据(a)与预处理后数据(b)
Fig.2 Original data (a) and pre processed data (b)
第3步使用Numpy和Scipy库对预处理后的数据进行快速傅里叶变换完成频域变化。以上文所述3颗星数据为例,所得频率值如图3。其中横坐标代表信号谐波频率。
第4步进行支持向量机模型训练。使用上述方法把747条光变曲线处理后获得数据集{f0,f1, ...,fd,T}。首先测试频率分量选择对模型训练的影响。用[fi,fj]表示从fi到fj的连续频率分量集合,用{fx,fy}表示fx,fy独立的频率分量集合。支持向量机模型选用线性核函数,训练集为373条数据,测试集为374条数据,惩罚因子设为1.0。其中,核函数是将输入空间映射到高维空间的函数算法,惩罚因子是对错误分类的容忍度,降低容忍度能获得更好的训练结果,但也可能产生过拟合。最终的结果如图 4。由图4可知,选取偶次谐波作为特征值时,分类正确率较高(图中数据a、b和c),即使仅用f0也可获得78.6%的分类正确率(图中数据a)。选择奇次谐波分量作为特征值时,正确率最高仅为57.8%(图中数据d、e),说明奇次谐波分量不适合作为特征值。比较图中结果f到i,正确率随着选取频率数量的增多而上升,说明选择更多频率分量有助于优化分类结果。训练集和测试集正确率相差小于2%,说明训练结果有效,且未达到过度训练。综合以上结果,偶次谐波分量适用于作为特征值。

图3 快速傅里叶变换的结果
Fig.3 Result of FFT
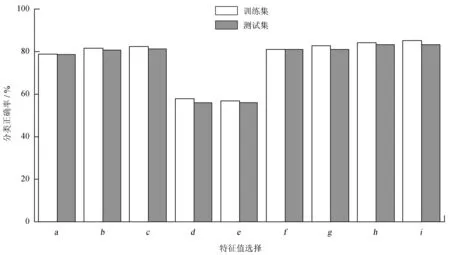
a{f0},b{f0,f2},c{f0,f2,f4},d{f1,f3},e{f1,f3,f5},f[f0,f2],g[f0,f4],h[f0,f6],i[f0,f8]
图4 分类正确率与特征值的关系
Fig.4 Relationship between classifying accuracy and characteristic value
2.2 支持向量机优化
优化支持向量机参数设置以获得更好的结果。支持向量机参数主要包括核函数选择和惩罚因子设置。选择不同核函数和惩罚因子,使用数据集{f0,f2,f4,f6,f8}作为特征值,所得结果如图5。由图5可知,4种核函数按优劣顺序依次为linear,rbf,sigmoid和poly。提高惩罚因子初期能显著提升linear,rbf和sigmoid的分类正确率,但在某一阈值后正确率达到稳定,惩罚因子对poly无影响。当选用linear核函数,惩罚因子设置为2.0时,获得最优分类模型,分类正确率分别为89.8%(训练集)和84.8%(测试集)。保存已训练好的模型用于其他新的光变曲线数据分类与识别。
2.3 实验结果分析与数据修正
由结果可知,训练所得模型正确率高,能满足分类需求,但仍有分类错误的数据。下面对分类错误的数据进行分析,找出分类错误的原因。
将分类错误的数据进行整理和分析,结果表明分类错误主要来自以下2方面:(1)两个网站的光变曲线和分类信息不一致,如AU Pup和AW Lac两个目标星的原始数据与预处理后数据如图6(a),由图可知该光变曲线类型应为EW型,但GCVS给出的光变曲线类型均为EB型,可修改原始光变曲线类型数据消除这种错误;(2)光变曲线类型分类缺乏明确的区分标准,如图6(b),GCVS给出XZ Cmi和SW Lyn分别为EB和EA型,但CALEB所给光变曲线数据非常接近,所以必需明确分类标准,并对原始数据逐条进行手工分类与核对,由于该工作量较大暂未进行。

图5 支持向量机参数与分类正确率关系
Fig.5 Relationship between SVM parameters and classifying accuracy

图6 分类错误的光变曲线
Fig.6 Light curve of classification error
我们修正了上文所述光变曲线与分类不一致的错误,共计14个目标,重新进行支持向量机模型训练和测试,结果如图7。由图5可知sigmoid和poly效果较差,这次仅进行linear和rbf两种核函数的测试。由图7可知linear核函数结果较好,当惩罚因子设置为5.8时,分类正确率为92.8%(训练集)和89.0%(测试集)。如果使用rbf核函数,当惩罚因子设置为5.6时,分类正确率为90.9%(训练集)和86.4%(测试集)。
使用linear和rbf两种核函数训练的模型对160条光变曲线数据[注]https://www.researchgate.net/profile/Y-G_Yang进行分类测试,分类正确率均为88.8%,检查错误类型,主要是EA和EB两种光变曲线分类错误。

图7 基于修正数据支持向量机参数与分类正确率关系
Fig.7 Relationship between SVM parameters and classifying accuracy based on the modified data
3 总结和展望
本文提出一种基于机器学习的光变曲线自动分类算法,使用快速傅里叶变换提取目标数据的频率,选用偶次频率分量作为光变曲线特征值,使用所提取特征值训练支持向量机模型获得分类模型。采用Python编程实现上述算法并进行优化,实验数据使用CALEB的实测光变曲线数据和GCVS的分类数据,结果表明,采用[f0,f2,f4,f6,f8]作为特征值时,选用linear核函数,惩罚因子设置为2.0可获得最优分类结果,分类正确率为89.8%(训练集)和84.8%(测试集),基本满足分类需求。
对分类错误的数据进行分析,结果表明,分类错误的第1个原因是CALEB的光变曲线数据和GCVS分类信息不一致,该类错误可以通过修改分类信息消除,第2个原因是光变曲线类型分类缺乏明确区分标准,某些非常接近的光变曲线数据被分为不同类型,对最终测试结果造成干扰,需要制定明确的分类标准并对原始数据重新分类才可以避免该种错误。将第1种错误全部修正后,正确率提升到92.8%(训练集)和89.0%(测试集)。由于未制定明确的分类标准,第2种错误还未修复。
在天文观测中自动化技术应用越来越广泛,获取的数据量也越来越多,在常规的观测数据中往往包含着我们感兴趣的特殊数据,预示着特殊的天文现象如双星合并等,需要筛选特殊数据,然后对该目标进行重点观测,能获得更有用的数据结果。如何从大量数据中快速筛选出特殊数据是一个难点。在随后的研究中将特殊光变曲线数据整理为样本数据,对支持向量机算法进行训练,使所得模型能够快速识别特殊光变曲线数据,从而能够快速响应。

