基于主成分分析法的本色布疵点分类算法

刘海军，单维锋，张莉丽，陈新房

(防灾科技学院 智能信息处理研究所，河北 三河 065201)

我国是世界上最大的纺织品生产国和出口国，纺织品的质量对纺织品的价格影响很大，研究表明：纺织品表面产生疵点会使其价格降低45%～65%[1]，因此纺织品的疵点检测对纺织品的质量控制至关重要。本色布又称坯布，作为纺织品的原材料，其质量直接影响着纺织品的质量。目前我国的本色布疵点检测主要由人工来完成，但人工验布方法存在很多缺陷，一方面，验布工人全神贯注的工作时间最多能保持30 min，此后，注意力明显下降，漏检、误检率很高，无法保证纺织品的质量；另一方面，验布车间高温、噪声、棉尘，对验布工人身体伤害极大，使得棉纺厂很难招到并留住合适的工人。

国内外针对本色布疵点检测方法的研究已有近30年的历史，其中的研究成果大致分为4类：统计方法、频域方法、模型方法及学习方法[2]，其中基于机器学习的疵点检测方法是近年来的研究热点，该检测算法中，图像的特征提取是关键环节，往往决定着检测效果，该类方法具有设计分辨性较强的特征。目前疵点检测领域通常关注针对疵点特征提取技术的研究，常见的特征提取方法有HOG特征(Histogram of Oriented Gradient,HOG)[3-5]、LBP特征(Local Binary Pattern)[6]、灰度共生矩阵特征[7]。由于疵点种类繁多(根据国家本色布检验标准，一共有71类疵点)，寻找一种万能的特征提取方法识别所有类型的疵点极其困难，目前文献中的特征提取方法，通常只检测3～5种明显疵点，少有研究者研究正常本色布纹理特征。本文从分析本色布编织方法开始，分析正常本色布纹理视觉特点，利用本色布纹理具有极强的自相关性特征，采用主成分分析技术(Principal Component Analysis，PCA)去除其相关性，得到纹理的主成分，进而在主成分方向上对样本图像进行压缩，将压缩的结果作为特征向量，采用最近邻分类器进行分类检测。实验结果表明，本文基于PCA的方法，在含有457幅训练样本，795幅测试样本的平纹平色布数据集上，取得高达99.11%的分类准确率。

1 本色布编织方法及图像视觉特征

本色布的纹理特征由纱线的材质和成分、纱线支数、织物密度、编织方法等4个因素决定，其中，影响最大的是编织方法。织物的编织方法有平纹、斜纹、缎纹 3种。图1示出了平纹、斜纹、缎纹经纬线编织示意图，同时示出了对应的本色布图像。可以看出，编织方法定义了经纱和纬纱的交错规律，这种规律使得坯布图像视觉上具有极其规律的相似性，坯布图像可以看作是由编织方法决定的纹理基元，沿着经向和纬向整齐排列。这种由编织方法导致的规律性，使得坯布图像局部之间存在着极大线性相关性，这种相关性增加了识别中的数据量与难度，因此可以对图像进行数学变换，去除其相关性，对图像数据进行压缩。

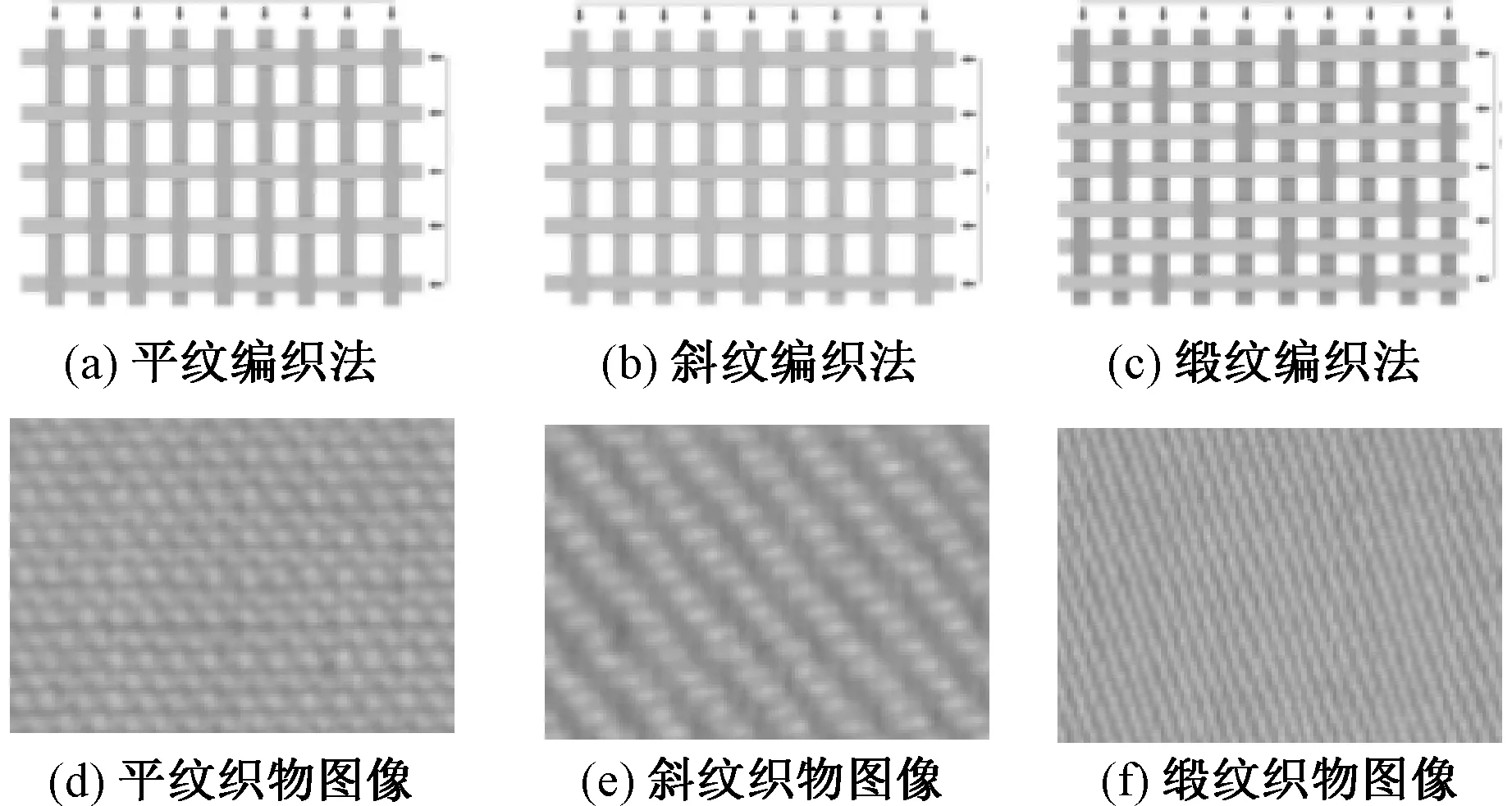
图1 坯布编织方法及效果示意图

本色布疵点类型很多，同一种类型的疵点形态多样，部分疵点图像见图2。可以看出，疵点图像彼此之间没有明显的共性，因此，从分析疵点的特征出发，找到万能的特征很难，但是疵点与正常纹理具有明显的差异。疵点的出现，破坏了坯布纹理基元的整齐排列，图像局部之间的自相关性变弱，因此，将正常坯布图像与疵点图像均进行去相关性处理，结果会有较大差异。

图2 部分疵点图像

2 坯布图像的主成分提取

通过前面的分析可知，坯布图像中的相关性增加了识别的难度。因此，在尽量减少图像中信息的同时，对图像进行最大限度压缩，去掉其相关性，有助于疵点识别，主成分分析法(PCA)恰好能解决该问题。

2.1 主成分分析(PCA)原理

PCA是一种统计方法，通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。PCA示意图见图3。其基本思想是最大方差理论，即沿着某个方向数据的方差越大，则该方向包含的信息越多，也就是所谓的主成分。假定数据只有二维，这些数据分布呈明显的椭圆形分布，该椭圆有一个长轴u1和一个短轴u2。在u1方向上，数据的分布比较散，方差较大，而在u2的方向上，数据变化较少，数据方差较小。椭圆的长轴u1和短轴u2的比值越大，则数据的相关性越强。极端情况下，短轴退化成一点，则一个方向u1即可描述数据了。图3中的u1就是主成分方向。

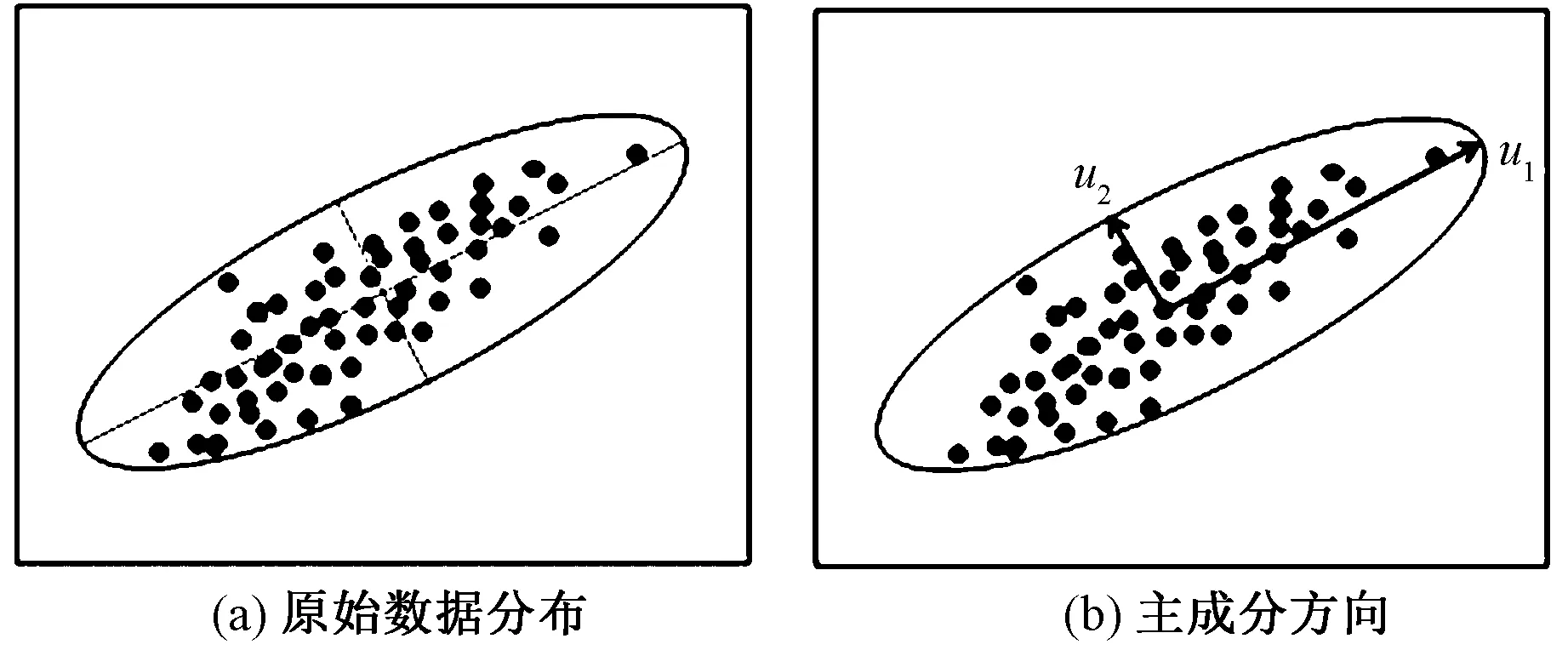
图3 PCA示意图

主成分分析通过对维数据做KL变换，找到k个主成分方向，并将原始数据投影到主成分方向，变换之后的数据为k维，达到了特征降维的目的。

2.2 本色布图像的PCA处理

本色布图像具有很强的线性相关性，因此采用PCA对图像进行降维处理，能极大地压缩图像的维度。图像的PCA处理过程如下：

①图像扁平化，构成样本矩阵。将每幅图像拉直，作为一个行向量；多幅图像的行向量纵向联合，构成样本矩阵。假设有n幅图像，每幅图像含有p个像素,则构成的样本矩阵具有n行p列。其中，每一行代表一个样本。然后对样本矩阵做去中心化处理，最终的去中心化样本矩阵为X=(X1,X2,…,Xp)n×p。

②求解协方差矩阵。样本数据的协方差矩阵为∑=∑(sij)p×p，其中:

(1)

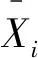
③利用奇异值分解，求解样本数据协方差矩阵∑的特征值λi及特征向量αi。

④利用特征向量构造投影矩阵对特征值λi进行排序，选择前k个特征值对应的特征向量构成投影矩阵：

Y=(αm1,αm2,...,αmk)p×k

(2)

式中：αmk为排序第k为的特征值λk所对应的特征向量;Y为投影矩阵。

⑤利用投影矩阵，对数据进行降维，计算公式为：

F=XY

(3)

经过变换后，F为PCA降维处理后的数据，其尺寸为n行k列，原始数据从p维降低到k维。

3 基于PCA的纺织品疵点检测实验

3.1 实验数据

实验选用平纹织物，图像原始尺寸为256像素× 256像素。部分实验图像见表1，实验样本数量分布见表2。

3.2 实验结果

将实验数据按照2.2算法进行特征降维，采用最近邻分类器进行分类，距离函数为欧式距离。实验中，将所保留的主成分数量n作为参数，实验结果见图4。

实验中n为最终保留的主成分个数，也就是最终的数据维数。原始图像尺寸为256像素×256像素=65 536像素，经过PCA处理后，被压缩成n维。

表1 部分实验图像

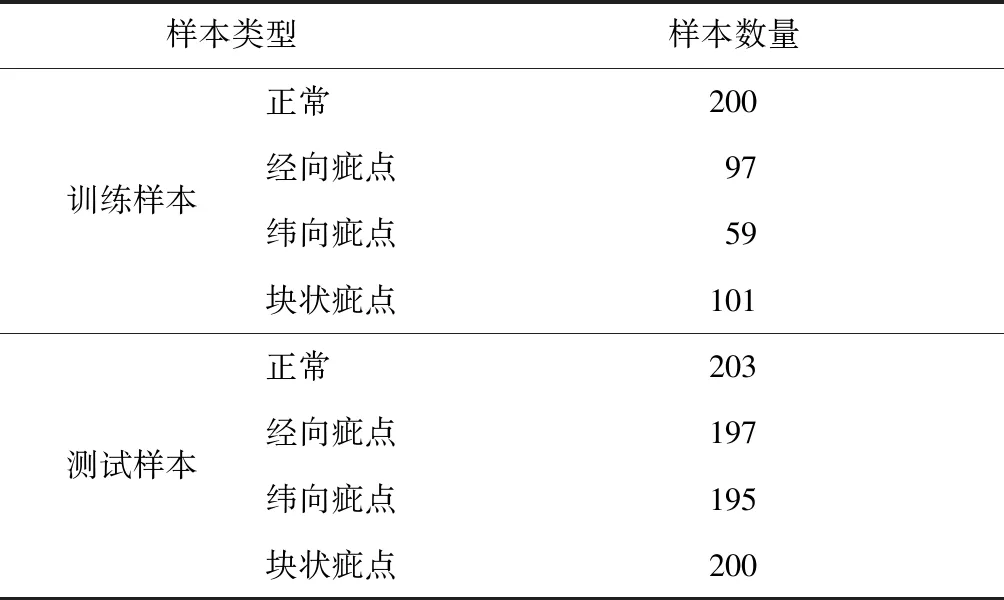
表2 实验样本数量分布

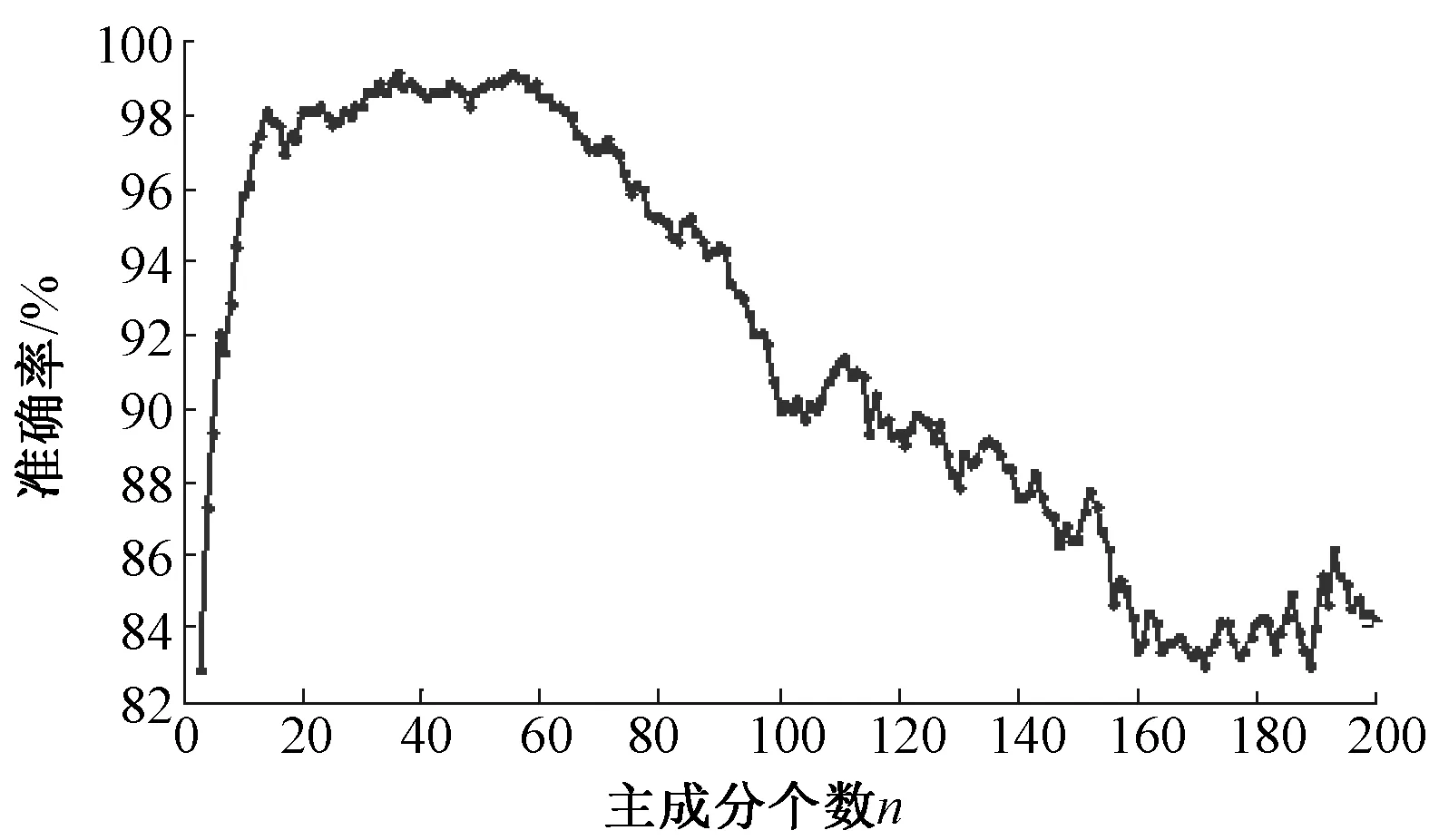
图4 实验结果

实验中n取其取值从3变化到200。从图4中可以看出，疵点分类的准确率随着k的取值呈现先增大再减小的趋势。当选择的主成分个数k较h(小于5时)，分类准确率不足99%。原因在于原始图像的尺寸为将65 536维数据压缩成较小的n时，数据损失过大，因此分辨性不强，导致识别率低。随着n的增加，压缩带来的数据损失越来越小，准确率因此上升。但是由于本色布图像中存在着大量的数据冗余，因此当n增加到一定程度，所保留的数据不再线性无关，使得问题趋于复杂，因此分类准确率下降。而当n取值达到60以后分类准确率下降明显，说明此时，压缩后的数据中开始出现线性相关性。实验中当n=33时，分类准确率达到最大，为99.11%。此时，数据压缩比为65 536/33，大约为1 900∶1。由此可见，本色布图像中数据冗余非常大。

将本文算法与梯度方向直方图(HOG)算法进行了对比实验，PCA与HOG的分类准确率分别为99.11%、94.70%。PCA算法明显优于HOG算法。

4 结 论

将PCA方法引入本色布疵点检测，首先建立样本矩阵并中心化，求样本矩阵的协方差矩阵，并对其进行奇异值分解，得到特征值和特征向量。然后将特征值从大到小排序，保留前k个特征值，并利用其对应的特征向量构造投影矩阵，最后将原始图像在投影矩阵上 进行投影，得到最终的压缩结果。文中采用最近邻分类器对压缩后的样本数据进行分类，准确率高达99.11%，比HOG方法提高了4.53%。研究表明：不需要对疵点进行复杂的特征提取算法，只需要利用本色布图像高度冗余的特点，对数据进行去相关性压缩，即可有效检测出疵点。