基于最小二乘支持向量机导弹订购价格预测模型研究

高卫刚 陈桂明 郭小川 蔺志强

摘 要：采取最小二乘向量机原理，创新性地以导弹武器装备性能作为训练参数，建立导弹订购价格预测模型，使之更加贴合部队实际。通过导弹作战任务需求，构建导弹武器装备性能指标，利用现有的数据，深入分析导弹武器装备性能与订购价格之间的关系，利用最小二乘支持向量机方法对数据样本训练优化，并应用实例进行了建模分析研究。

关键词：性能;最小二乘支持向量机;订购价格;预测

中图分类号：G641       文献标志码：A     文章编号：1673-291X（2019）26-0187-02

引言

采取最小二乘支持向量机（LS-SVM）法对导弹订购目标价格进行预测，预测结果与传统的支持向量机（SVM）预测结果相比较，不仅满足了预测的精度，而且也解决了模型计算的复杂性，提高了求解的速度，对导弹全寿命周期费用的预测具有较好的借鉴意义。

一、建模原理

最小二乘支持向量机是Suykens 和Vandewalb 在1999年提出的一种支持向量机变形算法。最小二乘支持向量机（LS-SVM）是基于正则化理论对标准支持向量机（SVM）的改进，此方法在各个领域得到了推广，并取得了较好的效果。

本文运用最小二乘支持向量机（LS-SVM）方法进行导弹订购价格预测，是将导弹订购价格起关键影响因素的性能与导弹订购价格数据相结合，以导弹性能作为导向，实质上是将影响导弹订购价格的关键性能参数作为输入的变量，具体的导弹费用数据作为输出，利用性能与费用数据作为训练样本，计算出相应的输出值，即导弹订购价格预测值。

将最小二乘支持向量机（LS-SVM）的建模思想融入到导弹订购价格预测中，核心思想也是通过某一个非线性函数Φ将训练样本映射到一个高维特征空间，在高维特征空间进行线性回归，从而取得在原空间非线性回归的效果。

二、建模过程及步骤

（一）建模过程

与常见的机器学习方法类似，运用LS-SVM方法估算费用也是一个数据拟合泛化问题，即先根据训练样本进行学习，确定系统结构和参数，然后对不在学习样本集中的輸入数据，计算出相应的输出值，即可得出估算结果。

（二）预测步骤

1.分析需要预测的系统，确定描述系统特征、性质的参数（或指标），构建LS-SVM的学习样本，包括输入参数数据和输出参数数据。在构造学习样本时，需要根据具体情况，对数据进行预处理，如对缺失数据进行完备、对连续数据进行离散化、对知识进行量化、对模糊数据进行量化等。研究采用4个特征参数进行分析，它们是作战性能指标，如有效载荷、最大标准射程以及圆概率偏差等。

2.选择核函数，确定初始的LS-SVM学习参数，然后输入学习样本到最小二乘支持向量机中进行学习，根据多次学习结果确定最佳学习参数γ、？滓2（RBF核），从而获得输入参数（影响费用参数指标）和输出参数（费用）的精确映射关系。

3.输入新的费用特征参数数据到训练好的支持向量机费用预测模型中，进行预测，对训练得出的模型的泛化能力进行验证。即输入测试样本验证训练模型的应用能力。LS-SVM常用的评价指标有平均绝对误差（MAE）、平方差（SSE）、均方差、平均相对误差（MAPE）、根方差或标准差（RMSE）、相对误差平方和（ESE）。本文采用MAPE和ESE进行结果评估。

三、性能参数的确定

（一）性能指标体系构建

根据导弹装备的特性，导弹装备的性能指标外延相当宽泛，这些性能指标不仅涉及的层面广，而且各性能指标之间存在错综复杂的关系。根据导弹作战任务的不同，选取关键的性能指标，找到导弹装备费用发生及变化的规律，建立完整且科学的性能指标体系是进行导弹订购价格预测的基础。基于性能对订购价格的预测，比费用分解结构更趋于实际，更贴近导弹部队的实战化需求。部队真正需要的是导弹武器装备作战使用性能，尽管某些新型导弹装备改良或新增的性能较之前的导弹较为突出，但没有提高导弹的作战使用性能，同时还增加了订购价格。因此，本文所涉及的性能重点考虑对部队实战和订购价格影响较大的作战使用性能作为研究依据。

（二）性能参数约束说明

基于性能的导弹装备订购价格预测不需要过多性能指标参与计算，只需要几个影响导弹订购价格的关键性能指标参与计算即可。目前来说，各系列导弹样本数量较少，为了防止出现过拟合的现象，筛选出关键的性能指标，将其中贡献较小的性能指标剔除。在剔除时，可以采用定性、定量分析和专家评定的方法进行筛选。

四、实例分析

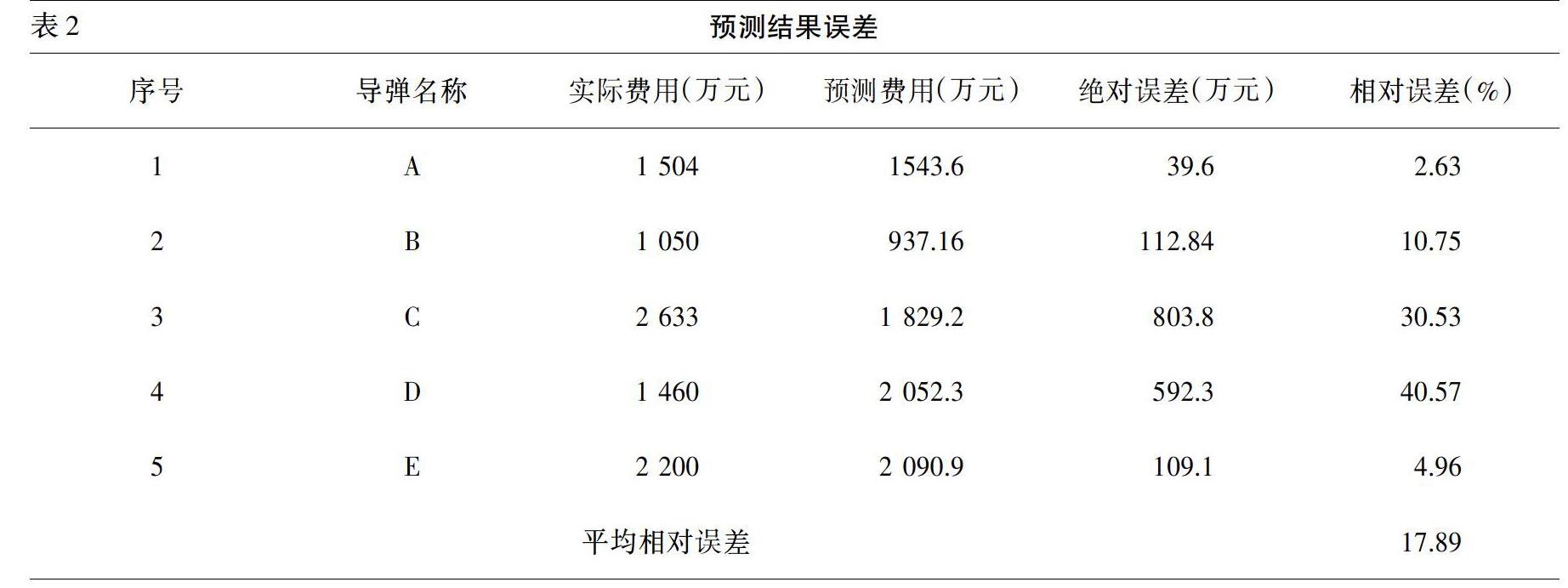
步骤一：通过对表1中5种型号的国外导弹历史数据进行样本训练，建立模型。

步骤二：预设定最小二乘支持向量机相关参数。sig2。这里主要通过经验的方法确定参数，多次重复计算，选择拟合效果最好的一次，从而得出费用估算的最小二乘支持向量机模型。本实例中，效果较好的一组核函数参数为gam（C）=200，sig2（σ2）=700，输入相关参数。

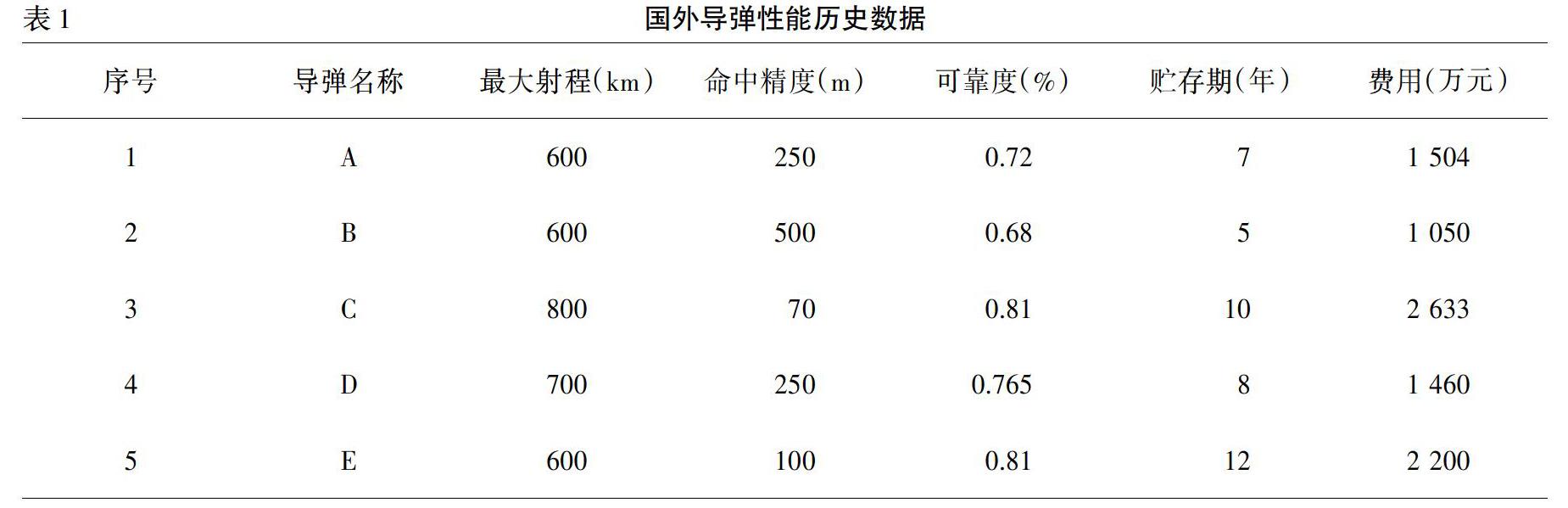
步骤三：数据输入，进行估算。预测时，每次轮空一个样本，其他样本作为训练数据，被轮空样本作为待估算对象。得到最小二乘支持向量机法的预测结果，如表2所示。其中，最小相对误差为2.63%，最大相对误差为40.57%，平均相对误差为17.89%。因此，LS-SVM方法用于导弹装备订购价格预测是可行的，预测结果比较理想。

结语

最小二乘支持向量机法使用较为简便，需要的历史数据量不大，具有良好的泛化能力，对新样本往往能显示出较好地推广能力，适用于新型号装备订购价格变动较大的预测，预测的结果准确度较高。另外，由于各个性能指标之间不牵涉权重问题，客观程度较高，但如果样本量不足且变量过多则容易导致过拟合，相对来说模型颗粒度大小会受样本的影响。因此，采取最小二乘支持向量机法构建导弹订购价格预测模型具有很高的借鉴价值，对提高装备建设发展的质量效益具有重要的军事意义和经济意义。

参考文献：

[1]  顾燕萍，赵文杰，吴占松.最小二乘支持向量机的算法研究[J].清华大学学报：自然科学版，2010，（7）：1063-1066.

[2]  高锽，孙德翔，邢国平.基于遗传算法优化支持向量机的航空装备维修费用预测[J].兵工自动化长沙，2011，（9）：24-27.