论大学数学在计算机专业课中的应用

郑素华 曾 钰 韩晓艳

（青岛工学院基础教育学院，山东 青岛 266399）

大学数学是理工类专业的基础课程，是每一个理工科学生必须学习的内容。大学数学包括高等数学、线性代数、概率论语数理统计三门课，对后续专业课的学习非常重要。但在实际教学中，常常有同学感到疑惑，大学数学对以后的哪些专业课到底有什么帮助。由于大学数学老师都是数学专业出身，往往并不是十分熟悉这些联系。本文通过三门课中的三个例子对这个问题加以讨论，希望对学生学习和教师教学有所帮助。

一、微分方程在信号与系统中的应用举例

我们在高等数学中专门有一章讲的是微分方程，其中线性方程是其中的重点，同济大学版本用了四节的内容介绍了一阶线性微分方、线性方程解得结构、高阶常系数齐次和非齐次线性微分的解法。在学习信号与系统这门专业课中，我们知道线性时不变系统是最常见的最有用的一类系统，描述这类系统输入-输出特性的是常系数线性微分方程。从微分方程出发，在时间域中研究输入信号通过系统后响应的变化规律，是研究系统时域特性的重要方法即时域分析法。

例1设有二阶系统的微分方程为y"（t）+5y'（t）+6y（t）=f'（t）求输入信号f（t）=9e-t·ε（t）的零状态响应。

解：由系统对应的特征方程λ2+5λ+6=0

得特征根λ1=-2，λ2=-3；将f'（t）代入原方程，有

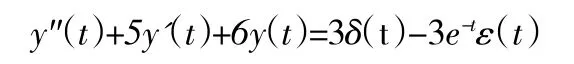
从而，F（t）=3ε（t）-3e-tε（t）x2（t）=(e-2t-e-3t)ε（t）故零状态响应

另外，分析工程上常用的周期和非周期信号的一些基本特性以及信号在系统中的传输问题时，傅里叶级数（对周期信号）和傅里叶积分（对非周期信号）是最基本的分析工具。当然，在各门专业课中常见的积分、微分表示的问题也非常多，限于篇幅，仅以此例说明高等数学是计算机各专业课的基础。

二、矩阵运算在数字图像处理中的应用举例

矩阵在计算机专业课中的应用随处可见，本文举一个矩阵运算在图形的几何运算中的例子。在某种意义上来说，图像的几何运算是与点运算相对立的。图像几何算法中国的图像平移、图像镜像、图像缩放和图像旋转都是通过矩阵的运算实现的。

1、图像平移

图像平移就是使图像沿水平方向或竖直方向平移。具体算法为：如果把坐标原点（0，0）平移到点（x0，y0）处，则变换公式为：

其中（x，y）是原图像坐标，（x'，y'）是变换后的图像坐标，图像中的各像素点移动了距离。此过程可用矩阵的运算表示为：

2、图像镜像

镜像是一个物体相对于一个镜面的复制品。分为水平镜像和垂直镜像两种。水平镜像用矩阵形式表示为：

垂直镜像用矩阵形式表示为：

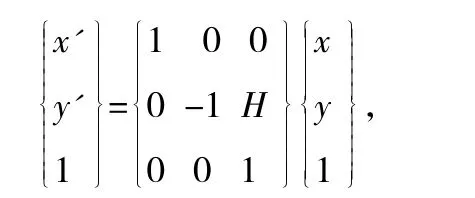
其中W和H分别表示为图像的宽和高。

3、图像缩放

图像的缩小和放大的定义是，将图像中的点（x，y）经缩小和放大后其位置变为（x'，y'），则两者之间的关系是：x'=ax，y'=by

a和b分别是x方向和y方向的放大率。a和b比1大时放大，比1小时缩小。当a=-1，b=1时，会产生一个关于y轴对称的镜像；当a=1，b=-1时，会产生一个关于x轴对称的镜像。此过程用矩阵表示为：

5、图像旋转

如果平面的所有点绕原点逆时针旋转θ0，则它的变换公式为：

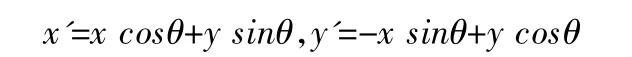
逆变换公式为：x'=x cosθ+y sinθ，y'=-x sinθ+y cosθ

用矩阵表示为：

另外，数学形态学是一门建立在严格数学理论基础上的学科，它已形成了一种新型的图像处理方法和理论，并成为计算机数字图像处理的一个主要研究领域。

三、贝叶斯公式在神经网络中的应用举例——贝叶斯分类器

20世纪90年代以来的一些理论分析和实验结果表明，很多情况下多层感知器的输出可以看作是对贝叶斯后验概率的估计。设所有训练样本的集合是X，其中属于ω1类和ω2类的样本的集合分别是X1和X，则训练的均方误差为：

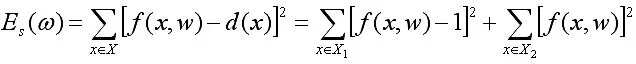
把样本x看作随机变量，其概率密度函数为p（x），设两类的先验概率分别是 p（ω1）和 p（ω2），p（x|ωi），i=1，2 是两类样本的类条件概率密度，p（ωi|x），i=1，2 是样本 x 属于 ωi的后验概率。设训练样本无穷大，且它们的分布反映真实的概率分布，则上面误差就成为：

利用贝叶斯公式

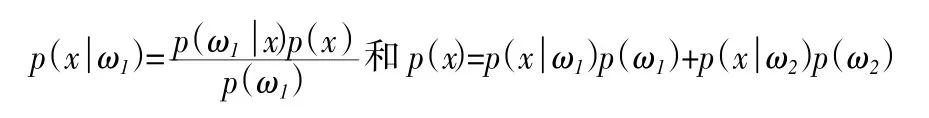
上式可转化为

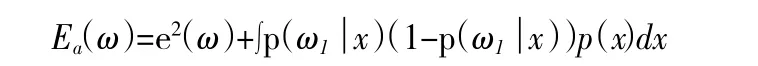
这说明：当训练样本为无穷多时，以使均方误差最小为目标训练的神经网络的输出在统计意义上是对样本后验概率的最小均方误差估计。

结语

由以上讨论，我们知道大学数学的知识点在计算机各专业课中的应用是非常广泛的.本文仅讨论了高等数学、线性代数、概率论与数理统计中各一个知识点的应用，当然大学数学对计算机专业课的基础作用不仅于此。比如，链式求导法则在深度学习的作用等，可以继续加以讨论。

另外，我们还可以讨论大学数学对建筑类专业课和机械类专业课的重要基础作用。从而，可以在教学中加以运用，正面回答同学们“学这些有什么用”的问题，进而提高课堂教学效果。