基于未知输入观测器的主动式座椅悬架鲁棒H∞控制

贾忠益,姜陶然,李 涛

(南京信息工程大学自动化学院,南京 210044)

近年来,主动式座椅悬架因最能提升乘坐的舒适性而备受关注.Gan等[1]设计了一种具有2个直线电动缸的主动座椅来减少传递至驾驶员的低频振动.Ahk[2]针对低频振动提出一种负刚度结构的气动减振系统.关于座椅悬架减振的控制策略主要有H∞控制[3]、滑模控制[4]和模糊控制[5]等,其中H∞控制器因求解和执行简单而成为研究热点.控制效果优的控制器设计离不开估计精准的观测器.在建立系统模型时,参数的不确定性及未知扰动干扰都会影响观测器的设计.对于含未知输入的系统,传统的观测器无法得到理想的估计结果.对未知输入具有鲁棒性但对故障较敏感的未知输入观测器在理论应用上引起关注.Chen等[6]结合未知输入观测器和故障检测滤波器进行鲁棒设计.Ting等[7]考虑了在状态和输出均未知的情况下估计MIMO线性系统状态的估计问题.然而,此类研究均须假定未知输入完全解耦,而本文将采用对未知输入无须完全解耦的观测器.由于加速度测量信号中容易混杂高频噪音,车辆座椅悬架控制很少使用加速度作为反馈量,故须设计合理算法有效估计摩擦力等扰动.摩擦力作为一种干扰,在要求仔细考虑的情况下对控制系统起着重要的影响作用,然而设计座椅悬架观测器时摩擦力一直被忽略或与系统干扰同等考虑.Ruderman等[8]设计了一种用于运动控制的非线性摩擦动力学观测器.本文拟基于可测量的座椅悬架系统位移、速度和加速度,利用未知输入观测器重构座椅悬架系统中存在的摩擦力,提出一种摩擦力补偿控制器设计方案,并通过仿真实验验证该控制算法的有效性.

1 主动式座椅悬架系统设计

图2 力矩扭矩转换示意图Fig.2 Force to torque transformation

选用如图1所示的新型主动式座椅悬架系统.该系统由旋转电机、齿轮减速器、跟随器、弹簧及凸轮结构等装置组成,系统结构简单,成本较低.执行机构模块由旋转电机和齿轮减速器组成,安装在剪刀式结构的旋转中心,以驱动悬架的垂直运动.机械装置为凸轮悬架结构.该凸轮被固定在一根剪刀杆上,当悬架负载时,凸轮沿着导轨推动跟随器移动,然后通过扩展弹簧支持外部负荷.

剪刀结构上力矩和扭矩之间的转换关系如图2所示.定义扭矩

(1)

式中F为摩擦力;L为剪刀结构杆长度,一般为常数,本文L=0.287 m;H为可测座椅悬架高度.

由于系统无阻尼器,故反应力由摩擦力和弹簧力组成.摩擦力建模为

F=CsgnV,

(2)

式中C,V分别表示库仑摩擦系数和相对运动速度.

2 控制系统设计

2.1 座椅悬架动力学模型

图3 座椅悬架系统模型图Fig.3 Seat suspension model

主动座椅悬架简化模型如图3所示,其中A为执行机构,k为刚度,c为阻尼系数,fr为滑动摩擦力,zs,zv分别为悬架上下部位移.主动座椅悬架运动控制方程为

(3)

式中m为司机、座椅悬架顶部平台和座垫的总质量，u为执行器主动力的控制律.

(4)

Y1=C1X,

(5)

Y2=C2X+D2(u-fr),

(6)

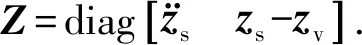
Z=C3X+D3(u-fr),

(7)

2.2 未知输入观测器设计

根据式(4)～(6)建立系统状态方程:

(8)

(9)

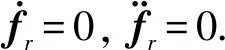
(10)

系统估计误差

(11)

(12)

(13)

K2=R0H,

(14)

则状态估计误差系统可描述为

(15)

下面将对上述座椅悬架系统进行如下假设讨论,为便于论述,C中包含C1和C2.

假设1rank(CB2)=rank(B2)成立.

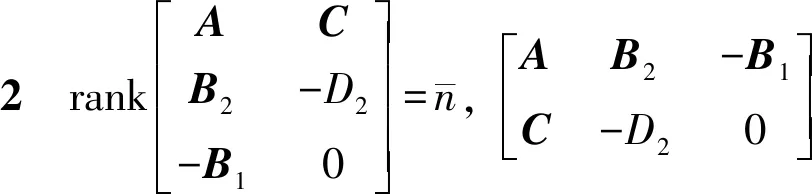
注1[9]假设1是为保证式(12)～(13)可解,并且存在一个特殊解

(16)

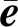
定理1对于系统(4)～(6),存在如式(10)所示的未知输入观测器,并满足性能指标:

(17)

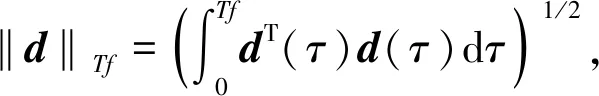
(18)

2.3 具有摩擦力补偿的控制器设计

构造状态反馈控制器

(19)

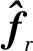
(20)

(21)

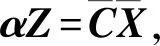
(22)

选择H∞范数为控制性能指标,定义

‖Tzd‖∞=sup(‖Z‖2/‖d‖2),

(23)

定义式(20)的Lyapunov函数

(24)

(25)

3 仿真分析

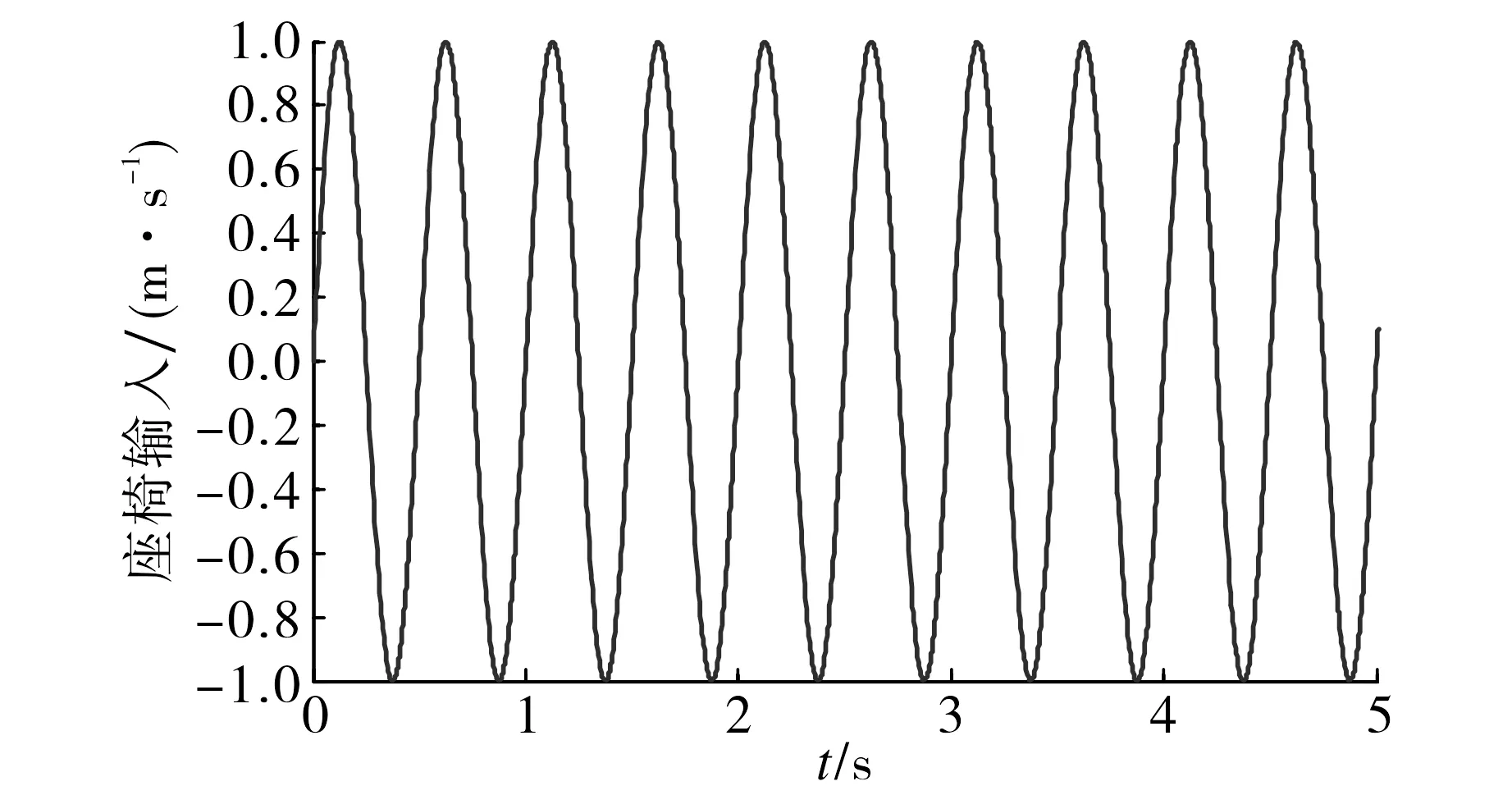
图4 座椅正弦输入Fig.4 Sinusoidal input for the seat

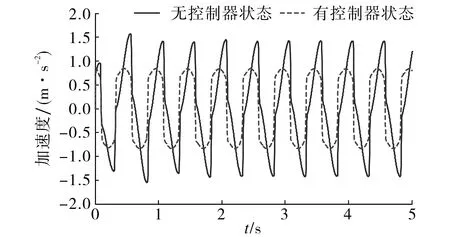
图5 座椅加速度Fig.5 Seat acceleration

图6 座椅位移Fig.6 Seat displacement

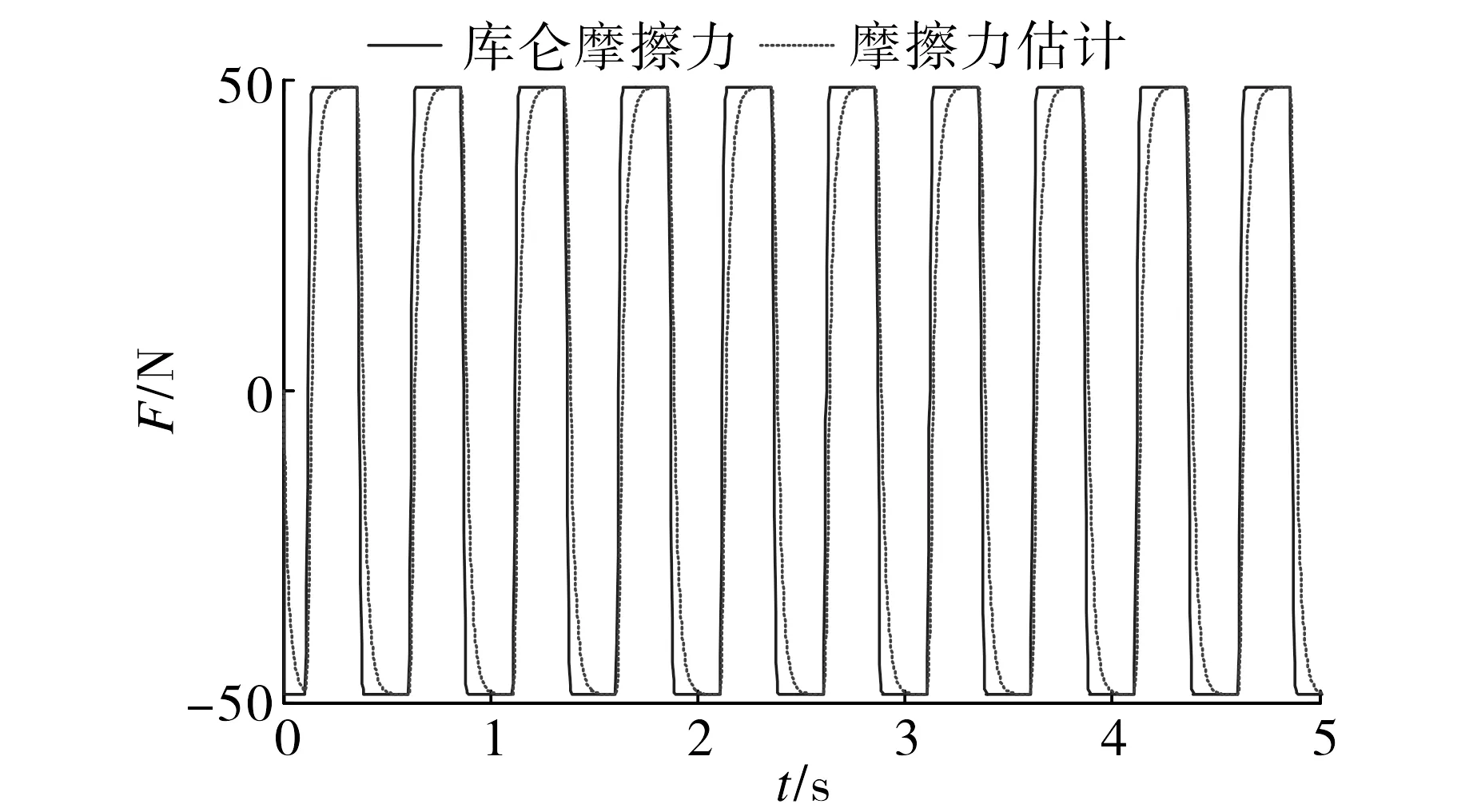
图7 摩擦力估计Fig.7 Estimated friction

图7为座椅悬架系统在未知观测器中重构的摩擦力估计与原系统实际摩擦力的对比结果.由图7可见,未知输入观测器在偏差允许范围内能较好地估计出系统中存在的摩擦力,可跟踪库仑摩擦力的变化，即若运动方向反转,库仑摩擦力发生变化时估计摩擦力在一定的位移周期内则随之逐渐逆转.