具有连续分布时变时滞神经网络时滞相关稳定性判据

刘 燕,于 传,黄永明,熊晶晶,刘 静

(1.南京工程学院工业中心,南京 211167;2.国网安徽省电力有限公司培训中心,合肥 230022;3.东南大学自动化学院,南京 210096)

由于时滞神经网络模型在实际应用中的重要性,时滞神经网络的时滞相关稳定性判据备受关注[1-2]．当考虑时滞信息,尤其是时滞较小时,时滞相关稳定性结果的保守性比时滞不相关稳定性结果低[3-5],故选择合适的Lyapunov-Krasovskii泛函 (LKF)对于得出具有更低保守性的稳定性判据至关重要[6-7]．为了获得具有更低保守性的结果,LKF导数估计是基于线性矩阵不等式推导稳定性判据的重要途径[3]．近几年,已经出现了多种估计LKF导数的方法,常用的有: 自由权矩阵[3,8]、积分不等式[6,9-10]、莱布尼茨-牛顿公式[11-12]以及这些方法的不同组合[3,10]．尽管可以使用这些方法来估计LKF的导数并减少保守性,但运算负担均较大．本文拟通过构造增广LKF,并利用多种积分不等式估计LKF的导数以获得更低的保守性和更小的运算负担,同时探讨时变时滞连续神经网络稳定性的条件．

在本文中,Rn表示n维欧几里德空间,P>0或P≥0表示P是一个真正的对称和正定(半)矩阵,对称矩阵中的对称项用*表示．

1 问题描述

时滞神经网络

(1)

其中神经元状态向量xt=[x1t…xnt]T∈Rn,f(·)为神经元激活函数,C=diag{c1,…,cn}(ci>0),A和B是权重矩阵,J=[J1…Jn]T是外部常量输入向量,τ(t)是时变时滞且满足

(2)

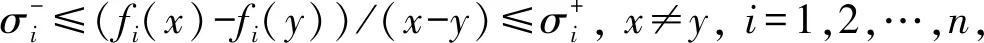
假设式(1)存在平衡点x*,则可通过改变变量值将此平衡点转移到原点,即yt=xt-x*,g(yt)=f(yt+x*)-f(x*),有

(3)

易得[6]

(4)

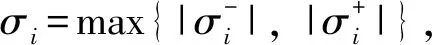
2 稳定性判据

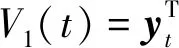
注1不同于文献[3-4,6]中的LKF结构,定理1中双积分项被扩充为V2(t)的形式,建立了状态变量与导数之间的关系．此外,通过构造函数V4(t),进一步构造了一个包含更多神经元活化函数斜率信息的全新LKF．

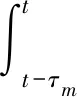
证明 考虑增广LKFVb(t)=V1a(t)+V2(t)+V3(t)+V4(t),其中

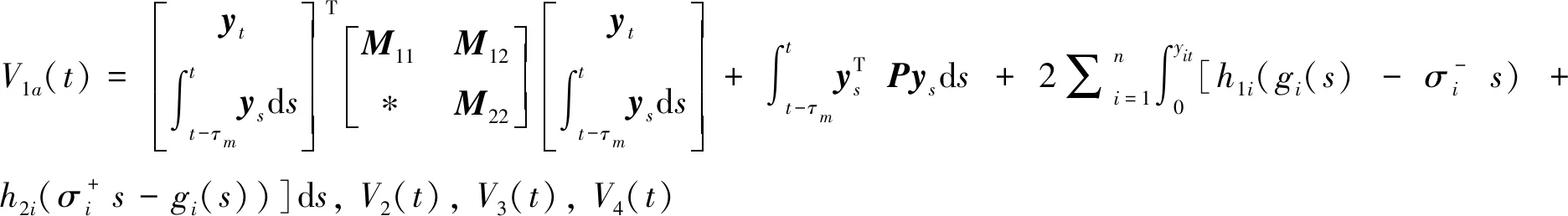
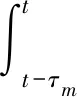
本文导出的稳定性判据给出了要确定的矩阵变量和用于保证时滞神经网络的稳定性基于LMI的约束条件,可以利用MATLAB/LMI 工具箱中的 feasp 函数从相应判据中求解这些变量．

3 数值算例

带参数时滞神经网络(3)[3]中

本文使用提出的定理1和定理2两个稳定性判据,获得了保证时滞神经网络全局渐近稳定性的可接受最大上界(AMUBs);文献[4,6,13]通过将时变时滞区间划分为2个子区间,给出了相应的AMUBs;文献[3]使用莱布尼茨-牛顿公式和自由加权矩阵技术保证有2个时滞分量的神经网络渐进稳定性,获得了改进的AMUBs．表1给出不同μ下所得AMUBs的结果．

表1 不同μ下AMUBsTab.1 AMUBs for various μ

从表1可以看到,本文方法的计算结果比文献[3-4,6,13]中的保守性更低,尤其当μ≥0.5时;条件2中当μ=0.9时,本文方法计算结果明显好于文献[3]中的结果,这是因为本文采用了几种合适的不等式代替了莱布尼茨牛顿公式和自由加权矩阵技术,并给出了神经元活化函数斜率的更多信息,说明新的增广LKF项改进了计算结果．为进一步说明本文所提方法的有效性,进行了仿真试验．

图1 神经元状态变量yit的状态轨迹Fig.1 State trajectories of neuron state variables

4 结论

本文研究了时变时滞连续神经网络的全局渐近稳定性,利用新的增广LKF和合适的积分不等式,导出了改进的时滞相关稳定性判据;考虑了更多神经元活化函数斜率信息的增广LKF已被用来降低稳定性判据的保守性．此外,由于本文并未涉及任何时滞分解和时滞分区的思想以及莱布尼茨牛顿公式和自由加权矩阵,得到的稳定性判据的计算负担已大幅减少,数值算例验证了本文方法的有效性．