具有死区输入和输出受限系统的动态面控制
李红春,夏梅珍
(1.扬州大学信息工程学院,江苏 扬州 225127;2.扬州工业职业技术学院电气与信息工程学院,江苏 扬州 225127)

1 问题描述及基本假设
考虑一类具有死区输入的未建模动态系统
(1)
其中Xi=[x1…xi]T(i=1,…,n)是系统可测状态,z∈Rn0是未建模动态项,q(z,Xn,t)是符合Lipschit条件的函数,hi(Xi,xi+1)是未知光滑函数,Δi(z,Xn,t)是动态扰动,f(Xn)和g(Xn)是未知光滑函数,D(t)是非线性死区模型输入u(t)的输出,y是系统输出,d+和d-为未知正常数,dr(u(t))和dl(u(t))为区间内的实际映射,均为平滑的未知连续函数.控制目标是构造控制律u(t),使系统(1)的输出y在死区输入等因素影响下自适应地跟踪给定输入yr,并确保闭环系统半全局一致最终有界,且|y|≤kc1(∀t≥0)成立,kc1是正常数.

根据假设1,死区模型可写为D(t)=H(u)u(t)+d(u(t)),其中
且min{kr0,kl0}≤H(u)≤min{kr1,kl1}=K,|d(u)|≤d*,d*=max{kr1,kl1}max{d+,d-}是未知常数.
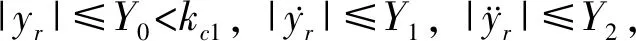
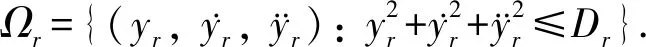
假设3增益g(Xn)符号未知,且满足0<|g(Xn)|≤gM,其中gM为未知正常数.
假设4存在均非负未知连续函数ρi1(·)和ρi2(·),且ρi2(·)为单调增,满足|Δi(z,Xn,t)|≤ρi1(‖Xi‖)+ρi2(‖z‖),i=1,…,n.
假设5[7]当指数输入状态z=q(z,Xn)渐近稳定时,有Lyapunov函数Q(z)使得α1(‖z‖2)≤Q(z)≤α2(‖z‖2),q(z,Xn)∂Q(z)/∂t≤-cQ(z)+γ(|x1|)+d,其中α1(·),α2(·)为K∞类函数;γ(·)为已知K∞类函数;c,d均为已知正常数.






2 动态面控制器的设计
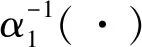


3 稳定性分析


4 仿真算例
非线性系统
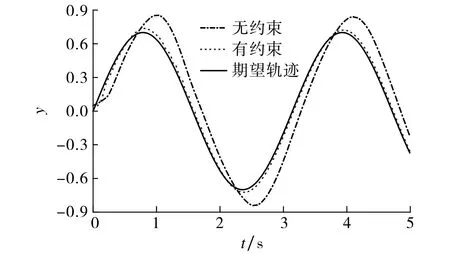
图1 不同情况下输出y与期望轨迹Fig.1 Output y and desired trajectory under two cases
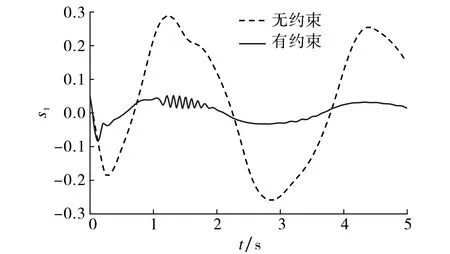
图2 不同情况下的跟踪误差s1Fig.2 Tracking error s1 under two cases

