一类非线性抛物积分微分方程的非协调有限元方法
2019-04-16 06:01李先枝王志军
扬州大学学报(自然科学版) 2019年1期
李先枝,王志军
(郑州师范学院数学与统计学院,郑州 450044)
抛物方程是一类重要的方程,其常见数值解法有:研究抛物型积分微分方程的混合有限元方法[1-2]、利用线性化格式及双网格法研究非线性抛物型方程的超收敛分析和最优误差估计[3-4]、用线性化Galerkin有限元方法研究非线性抛物方程[5]等.带有阻尼项的非线性抛物方程
(1)
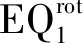
1 单元的构造及逼近格式

((u-Ihu),
(2)

(3)
相应的半离散问题为: 求uh∈Vh,使得
(4)
2 半离散格式下的超逼近分析
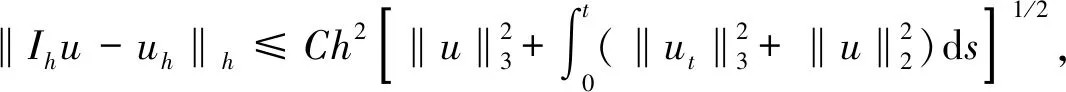
证明 取u-uh=u-Ihu+Ihu-uhξ+θ,由式(3)(4)得
(θt,vh)h+(hθ,hvh)h=-(ξt,vh)h-(hξ,hvh)h-(|u|2u-|uh|2uh,vh)h+
∀vh∈Vh.
取vh=θt,有θ(X,0)=0,则
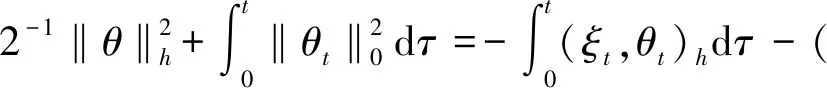
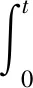

3 全离散格式及误差分析
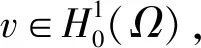
(5)
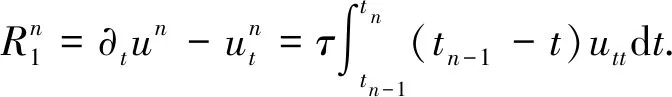
(6)
定理2设un,Un分别是式(5)(6)的解,u,ut∈H3(Ω),utt∈L2(Ω),则‖un-Un‖h=O(h+τ).
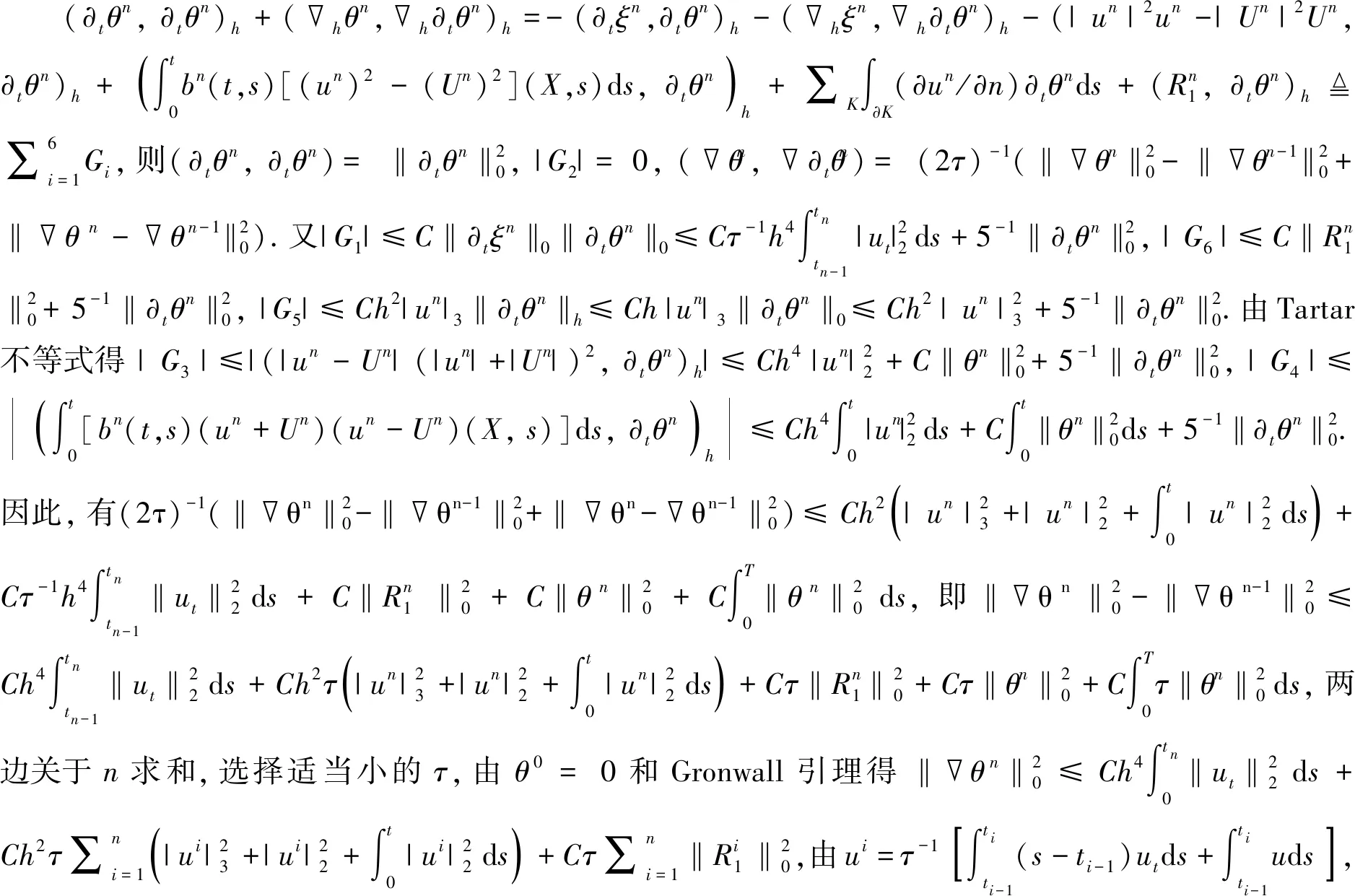
猜你喜欢
法律方法(2022年2期)2022-10-20
中等数学(2020年2期)2020-08-24
科技风(2020年13期)2020-05-03
数学物理学报(2019年5期)2019-11-29
科学与财富(2019年3期)2019-02-28
科技创新导报(2019年24期)2019-01-14
小天使·一年级语数英综合(2018年11期)2018-11-23
小学阅读指南·低年级版(2018年5期)2018-11-02
江西建材(2018年3期)2018-03-21
湖北农业科学(2017年11期)2017-07-13

