一类具有纽曼边界条件的无限半正定p-Laplacian外问题的正径向解的唯一性*

吕艳春

(广西师范大学 数学与统计学院,广西 桂林541006)

0 引言及主要结果

考虑以下的边值问题

在文献[2]中,Chu,Hai和Shivaji利用解的估计和反证法得到了(1)在满足Dirichlet边界条件下的正径向解的唯一性,还得到了解的渐进性.注意到,在文献[2]中(1)在u=0处可能具有无限半正定结构,且不要求f是单调的.文献[3]研究了(1)在半正定条件下(f(0)＜0)的正经向解的唯一性,且要求f是单调的.此外,文献[2-3]所得到的结果都要求λ≫1.对于当λ≫1时的唯一性结果还可以参见文献[4-6,8].

文献[8]研究以下边值问题的正解的存在性与唯一性：

其中0≤α＜1,c：[0,∞)→(0,∞),h：(0,1)→(0,∞)都是连续函数,且λ是一个正参数.该文在对f和h的一些假设条件下,利用上下解的方法得到了问题(3)在λ≫1时至少有一个正解,并且还证明了问题(3)在α=0时有唯一正解.对于当λ≫1时的存在性结果还可以参见文献[1,9,11].

我们对f(z)和h(t)作如下假设：

注意到在(H5)的条件下,问题(2)在u=0处可能具有无限半正定结构.特别地,若(H1)～(H3)成立,问题(2)在λ≫1时至少有一个正解.[8]

在上述假设条件下,得到主要结果如下：

定理1：假设(H1)～(H5)成立,则当λ＞λ0时,问题(2)有唯一正解.

1 一些引理

本节介绍一些在定理1的证明中将要用到的引理.

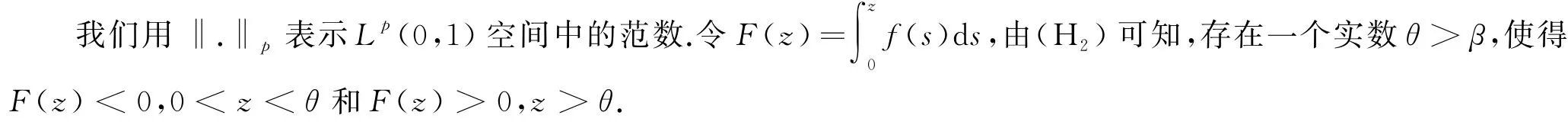
引理1[7,11]对∀x,y∈ℝ,当1＜p＜2时,有

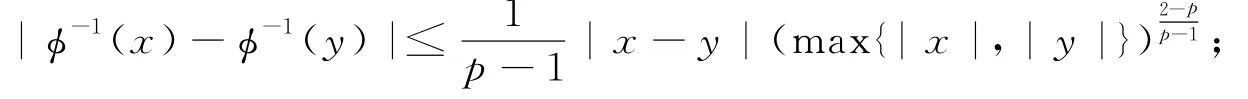
当p≥2时,有|ϕ-1(x)-ϕ-1(y)|≤2ϕ-1(|x-y|).

引理2[2]令u(t)是(2)的一个正解,则u(t)在(0,1)内有唯一的最大值,记为u(t0),且u(t0)≥θ.

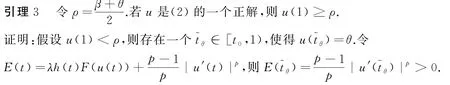
因为u(t)在[t~θ,1]上递减,所以u(t)≤θ,t∈[~tθ,1],从而有E'(t)=λh'(t)F(u(t))≥0,

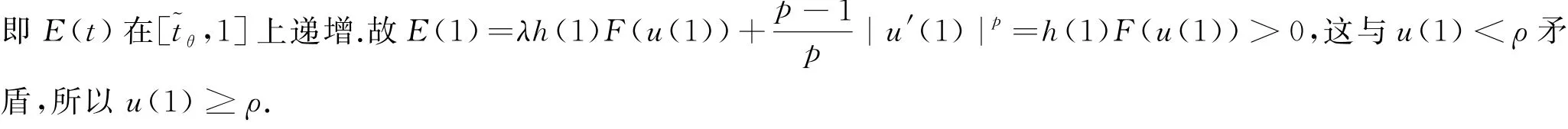
引理4[2]令tρ∈(0,t0)使得u(tρ)=ρ,则存在一个常数cρ＞0,使得(2)的任何一个正解u(t)满足

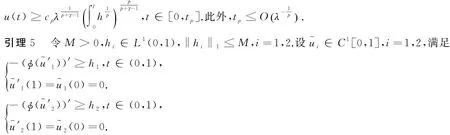
则 (i)给定一个ε0＞0.如果h2≥0,h2≢0,且存在常数δ＞0,使得‖h1-h2‖1＜δ,则有

证明：令ui∈C1[0,1],i=1,2,满足

由弱比较原理(见文献[10]的Lemma A.2)得,~u1(t)≥u1(t),u2(t)≥~u2(t),∀t∈[0,1].令ε＞0.下面证明若存在δ＞0,使得‖h1-h2‖＜δ,则‖u'1-u'2‖∞＜ε.

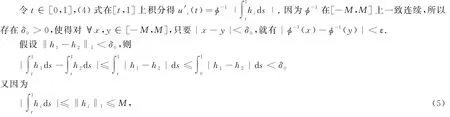
所以|u'1(t)-u'2(t)|＜ε,t∈[0,1].因此,只要取δ=δ0,这就证得若存在δ＞0,使得‖h1-h2‖1＜δ,则‖u'1-u'2‖∞＜ε.

现证(i)成立.若h2≥0,h2≢0,则u2(t)≥‖u2‖∞t,t∈[0,1](见文献[7]的Lemmma 3.4和文献[11]的Lemma 2.2).由上述的证明可知,|u'1(t)-u'2(t)|＜ε,∀t∈[0,1].因为u1(0)=u2(0)=0,利用中值定理得u1(t)≥u2(t)-εt,t∈[0,1].令ε＜ε0‖u2‖∞,则u1(t)≥(1-ε0)u2(t).故~u1(t)≥(1-ε0)~u2(t),t∈[0,1].

现证(ii)成立.由引理3可知,当1＜p＜2时,

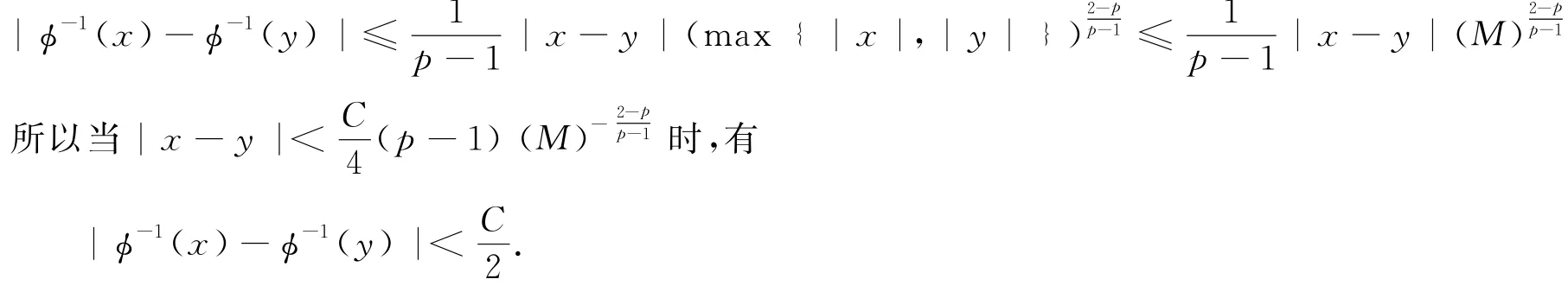
由引理3可知,当p≥2时,|ϕ-1(x)-ϕ-1(y)|≤2ϕ-1(|x-y|).

引理7 若存在常数λ～＞0,使得λ＞λ～,则存在常数C0＞0,使得(2)的任何一个正解u(t)满足

将(8)式的不等号的右边定义为h1,由引理6得,h1∈L1(0,1).令w∈C1[0,1]满足

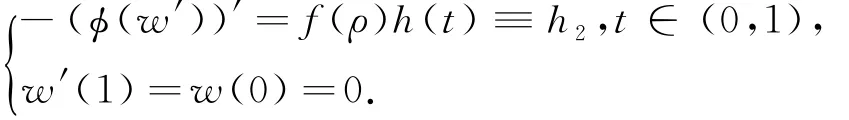
则w(t)≥ ‖w‖∞t,t∈[0,1](见文献[7]的Lemmma 3.4和文献[11]的Lemma 2.2).因为所以当λ足够大时,有

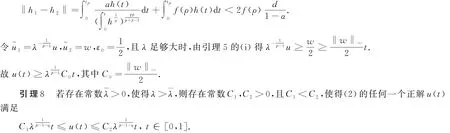
证明：令ε∈(0,1),由(H5)知,存在一个常数m＞0,使得

(L-ε)zq≤f(z)≤ (L+ε)zq,z＞m.

若λ＞λ～,由引理7知,u(t)≥.令dλ是使得u(t)≥dλt成立的最大常数.

因为φ≥‖φ‖∞t(见文献[7]的Lemmma 3.4和文献[11]的Lemma 2.2),所以

2 主要结果的证明

为了利用上述引理7～9,我们假设λ＞1是足够大的数.

定理1的证明：令u,v是问题(2)的两个正解,由引理8知,

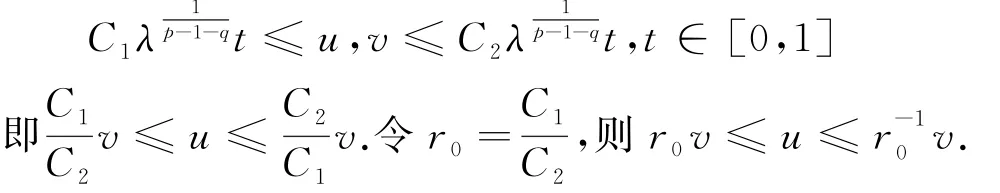
令r1是使得r1v≤u≤r-11v成立的最大常数,并且我们假设r1＜1.

因此

由(12)式知,hi∈L1(0,1),i=1,2.所以有

其中k4＞0是一个与r0,k3和p有关的常数.因为λ→∞时,‖h1-h2‖→0,所以当λ足够大时,我们有

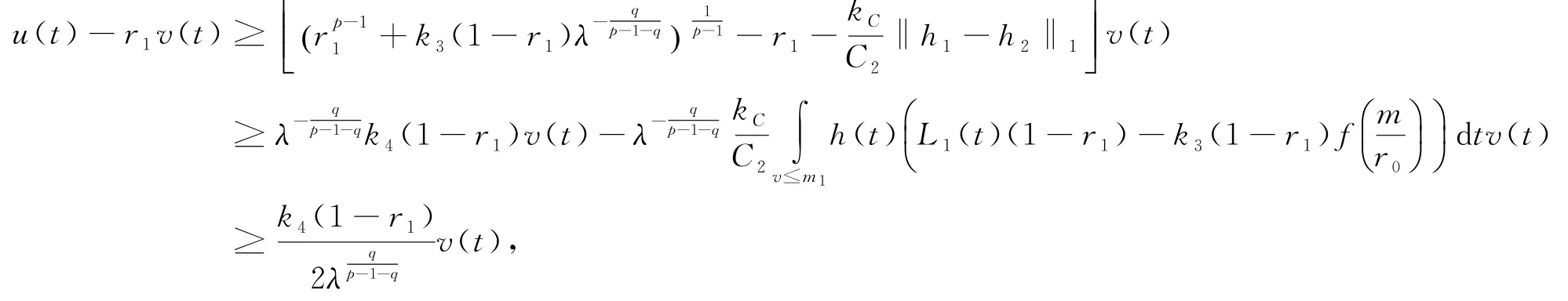
所以存在一个实数r2＞0,使得

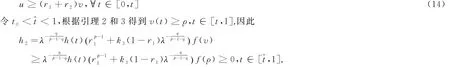
所以

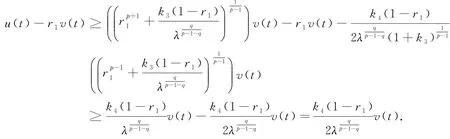
因此,存在一个实数r3＞0,使得

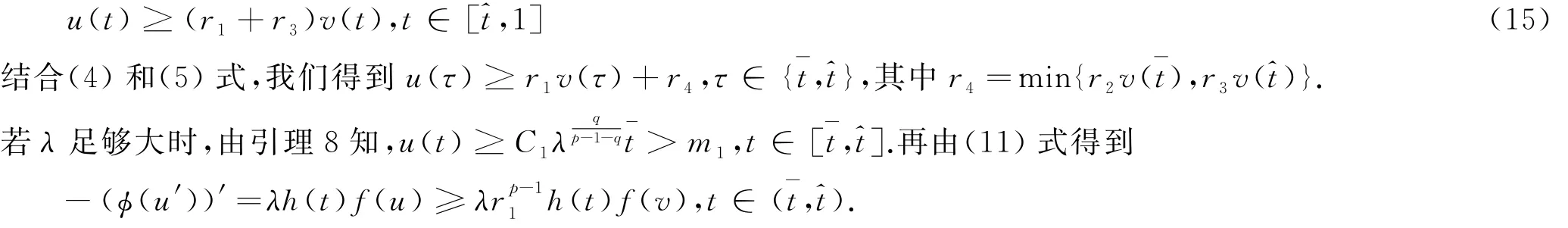
又因为

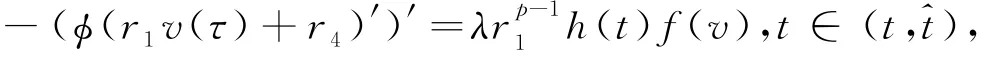
且u(τ)≥r1v(τ)+r4,τ∈ (t^,t).因此,利用弱比较原理(见文献[10]的Lemma A.2)得到

结合(14)～(16)式得到,存在一个实数r5＞0,使得u(t)≥(r1+r4)v(t),t∈[0,1].类似地,也可以得到存在一个实数r6＞0,使得v(t)≥(r1+r6)u(t),t∈[0,1].因此,存在一个实数r～＞0,使得(r1+r～)v(t)≤u(t)≤(r1+r～)-1v(t),t∈[0,1].这与r1是使得r1v≤u≤r1-1v成立的最大常数矛盾,所以r1≥1.这意味着u=v,t∈[0,1].