心理与教育元分析中相关系数的范围限制矫正*

李金德

(广西民族大学 教育科学学院,广西 南宁 530006)

0 引言

效度概化(validity generalization)是1977年由Schmidt提出的一种研究人事选拔测量工具效标效度的研究方法,[1]作为一种元分析(meta-analysis)研究范式已经被许多研究领域采纳,也包括心理与教育元分析领域.效度概化研究者认为因为统计误差的存在致使测量工具的效标效度变异性被严重高估而它的大小却被严重低估,只要将这些统计误差剔除就会发现测量工具效标效度的真实大小和跨情境一致性,这便是效度概化的过程.常见的统计误差有测量误差、抽样误差、范围限制、效标污染、计算和输入误差等,[2]目前效度概化研究中能矫正的主要是测量误差、抽样误差和范围限制.范围限制的矫正比测量误差和抽样误差的矫正复杂,鉴于国内该领域研究的匮乏,本文拟就如何矫正相关系数的范围限制做相应介绍.

1 范围限制

效标效度研究的目的是判断预测变量X对总体被试的效标行为Y的预测作用,但是研究所能获取的被试常常不是总体而是某种群体,这种群体的获取方式很多,理想的方法是随机抽样.但在人员选拔和教育选拔的研究中,能获取的群体通常只由那些通过某个分数点的人组成,这种选取被试的方式,本文称为截取.因为被试是被截取的,所以其取值范围受到了限制,这便是变量的范围限制(range restriction).那些因为某种截取方式而保留下的被试称为受限群体,而那些受限群体背后的总体称为未受限群体.[3]

范围限制有直接范围限制(direct range restriction)和间接范围限制(indirect range restriction)之分.[4-5]假如研究者要探讨X预测效标行为Y的效度,测试了一个群体,然后将X分数由高到低进行排序,但最后只截取该群体的某个分数段的被试作为研究对象,如只截取高于X平均值的被试,此时X的取值范围受到了直接限制,这便是直接范围限制;假如研究者在筛选被试时依据的标准不是预测变量X的取值,而是第三个变量S,因为S与X有关联,所以对S的直接截取会间接影响X的取值范围,这便是间接范围限制.一般情况下,因为存在范围限制,受限群体的方差会比未受限群体低,这样会降低X与Y的相关系数,[6-7]Thorndike(1949)提出矫正公式CaseⅠ、CaseⅡ和CaseⅢ进行矫正,后来又有研究者提出了CaseⅣ和CaseⅤ.本文将结合元分析的步骤对这几个矫正公式做介绍,为方便论述下文将受限群体测量指标用下标“i”表示,将未受限群体测量指标用下标“a”表示,另外限于篇幅下文公式中的字母指代只在第一次出现做解释.

2 直接范围限制的矫正

2.1 CaseⅠ

如果直接范围限制发生在预测变量X上,但X的未受限方差未知,而效标变量Y的未受限方差已知,可以使用CaseⅠ对相关系数进行矫正,[8]即

式中,RXY为矫正范围限制后的相关系数;rXY为受限相关系数;uY=sY/SY,sY和SY分别表示Y的受限和非受限标准差.

因为CaseⅠ的适用条件不常见,所以很少被使用,[8-10]相比较而言CaseⅡ的使用就很频繁.

2.2 CaseⅡ

2.2.1 单个因素矫正

如果直接范围限制发生在预测变量X上,且X的未受限方差已知,可以使用CaseⅡ对相关系数进行矫正,[8]即

式中,uX=sX/SX,其中sX和SX分别表示X受限和未受限标准差.

CaseⅡ有两个基本假设：[11]第一,线性假设,即受限群体和未受限群体中效标变量对预测变量的回归系数(斜率)是相等的;第二,方差同质性假设,方差同质性假设要求未受限和受限群体的残差方差相等.

2.2.2 元分析矫正步骤

利用CaseⅡ的矫正公式,Hunter和Schmidt构建了同时考虑信度和范围限制时相关系数的元分析矫正步骤,[12]图1可用来描述该矫正过程.图中T表示预测变量的真实值,X表示预测变量的观测值,T是无法测量的,可以理解为潜变量,它由显变量X表征;同样的,P表示效标变量的真实值,Y表示效标变量的观测值,P也是潜变量,由显变量Y表征;X上的虚线表示直接从变量X的分数上截取被试,即直接范围限制发生在X上.

图1 CaseⅡ直接范围限制模型Fig.1 CaseⅡdirect range restriction model

假如每个研究的预测变量和效标变量的受限与未受限信度已知,同时预测变量的受限和未受限方差已知,此时元分析的基本思路是对每个研究的相关系数进行逐个矫正然后加权合成总系数,[12]步骤如下：

第一,矫正Y的受限信度rYYi对ρXYi的影响得到校正系数ρXPi,即

式中,ρXYi指每个研究的受限相关系数.

第二,矫正X的直接范围限制对ρXPi的影响得到矫正系数ρXPa,即

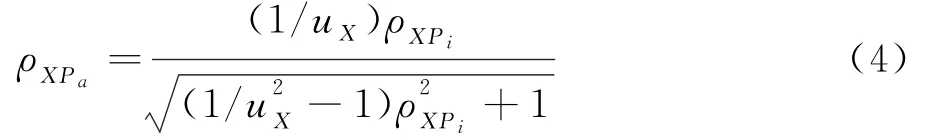
第三,利用受限信度rXXi和u2X估算X的未受限测量信度rXXa,即

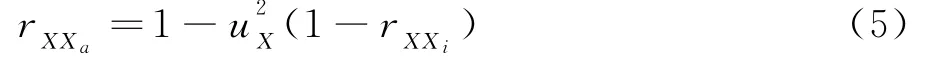
第四,矫正rXXa对ρXPa的影响得到单个研究较正系数ρTPa,即

式中,ρ指合成的平均效应量(总效应量);ρj指第j个研究的矫正效应量,即ρTPa;wj指第j个研究的权重,可以是该研究的样本量或方差倒数,[13]也可以是联合权重.[2]

如果个体研究未受限群体的信度和方差未知,研究者可以利用一些假设分布作为相关指标的计算依据,[1]步骤如下：

第一,计算受限相关系数的平均值,即

式中,ρXYi指平均受限相关系数;wj指权重,通常为方差倒数.[13]

第二,根据先验知识构建假设分布以获取变量信度和范围限制比率等信息.[1]要获取的指标有X的信度均值rXX、Y的信度均值rYY、X的范围受限比率均值uX.

第三,将所有指标带入以下公式便可获得总相关系数ρTP,即

2.2.3 对CaseⅡ的评价

早期研究者们的模拟和实证研究显示CaseⅡ的矫正效果较为理想.[14-15]研究者还发现当违背方差同质性假设时,CaseⅡ 的矫正结果仍然很稳健,但CaseⅡ的矫正结果对违背线性假设却非常敏感.[9]CaseⅡ面临最大的质疑是现实研究中大部分的范围限制是间接而非直接的,此时用CaseⅡ矫正范围限制会低估效度,[10]研究者认为CaseⅡ早期的模拟研究之所以较理想不过是因为模拟的都是直接而非间接范围限制案例.[12]总之,间接范围限制应该采用与之对应的公式而非CaseⅡ.

3 间接范围限制的矫正

3.1 CaseⅢ

若直接范围限制发生在变量Z上,但因为Z与变量X有关,所以对X的取值产生了间接影响,进而影响X和Y的相关系数,此时可用CaseⅢ对相关系数进行矫正,[8]即

式中,rXY为X和Y的受限相关系数;rXZ为X和Z的受限相关系数;rYZ为Y和Z的受限相关系数.

使用CaseⅢ要假设X只受到Z这一个变量的影响,但影响X的变量常常是几个而较少是一个.即使X确实只受一个变量Z的影响,要获知rXY、rXZ、rYZ、sX和SX也十分困难,所以CaseⅢ很少被使用.[16]矫正公式caseⅣ的出现弥补了CaseⅢ的缺陷.

3.2 CaseⅣ

3.2.1 单个因素矫正

CaseⅣ需要的计算条件比CaseⅢ少,具有实践应用价值.图2是CaseⅣ的模型图,该模型比图1的模型增加了一个新变量S.[12]S相当于CaseⅢ中提到的Z变量,不过S变量在这里指的是潜变量,Z没有这样的假设.S的统计信息与Z一样常难以获取,有时因为没有测量,更多时候是因为S是一个组合体而根本无法测量.在CaseⅣ中,对被试的截取首先直接发生在S上,而因为S和预测变量有关系,所以对S的直接截取会间接影响到预测变量的分数分布,即发生了间接范围限制.需要注意的是,变量S是作用于预测变量的潜变量T而不是显变量X.CaseⅣ同时还假设S对效标变量潜变量P的影响全部被T中介.

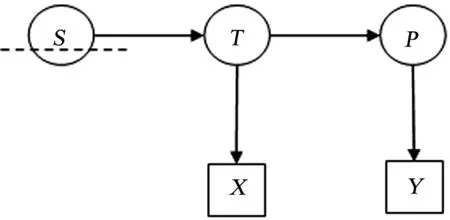
图2 CaseⅣ间接范围限制模型Fig.2 CaseⅣindirect range restriction model

在CaseⅣ中,关键是要估算出预测变量T的范围限制比率uT,[2]即

式中,uT指潜变量T的范围受限比率;rXXa是X未受限测量信度.

在只有范围限制因素时,CaseⅣ对相关系数的矫正和CaseⅡ相似,即

3.2.2 元分析矫正步骤

假如每个研究的预测变量和效标变量的受限与未受限信度已知,同时预测变量的受限和未受限方差已知,可以对每个研究的相关系数逐个矫正然后将它们加权汇总,步骤如下：

第一,矫正Y的受限信度rYYi对ρXYi的影响得到校正系数ρXPi(参考公式(3)).

第二,估算X的受限信度rXXi,即

如果rXXi已知,可以直接到第三步.

第三,矫正rXXi对ρXPi的影响得到较正系数ρTPi,即

第四,估算X的未受限测量信度rXXa,即

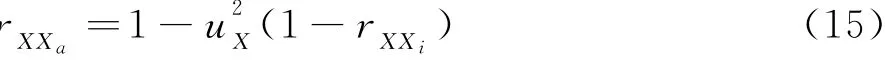
如果rXXa已知,可以直接到第五步.

第五,对T的范围受限比率uT进行估算(参考公式(11)).

第六,将指标带入以下公式得到单个研究未受限相关系数ρTPa,即

第七,计算总的效应量ρ(参考公式(7)).

如果个体研究未受限群体的信度和方差信息不全,与CaseⅡ一样研究者可以利用一些假设分布作为相关指标的计算依据,步骤如下：

第一,计算受限相关系数的平均值ρXYi(参考公式(8)).

第二,根据假设分布获取X的信度均值rXX、Y的信度均值rYY、X的范围受限比率均值uX,并利用rXX和uX,计算出uT,即

第三,将所有指标带入以下公式便可获得总相关系数ρTP,即

3.2.3 对CaseⅣ的评价

CaseⅣ假设发生在S上的直接限制对T产生间接范围限制,同时假设S对P的影响全部通过T产生,假如这个假设成立,CaseⅣ和CaseⅢ在数学上是等价的.与CaseⅢ比,CaseⅣ让间接范围矫正成为可能,[17]与CaseⅡ比,CaseⅣ对间接范围限制的矫正更准确.[18-19]当然,CaseⅣ对S、P和T的间接路径假设在实际研究中很难满足,[17,20]因为用于截取被试的变量S常常是未知的或者因为组合复杂而难以测量,这样S与T和P的间接路径就难以确定,基于此,研究者提出了矫正公式CaseⅤ.

3.3 CaseⅤ

3.3.1 单个因素矫正

在间接范围限制中,如果第三个变量S与预测变量X和效标变量Y的相关是同向的,可以利用以下公式对相关系数进行矫正,[21]即

如果S与X和Y的相关是反向的,即一个为正,一个为负,可以利用以下公式对相关系数进行矫正,[22]即

公式(19)和公式(20)主要针对的是显变量层面的相关系数矫正,从CaseⅣ中获得灵感的Le等人[10]将其应用到潜变量层面的相关系数矫正,并且将其命名为CaseⅤ,其模型见图3.从图3可见,CaseⅤ模型比CaseⅣ模型多了一条从S到P的路径,它表示S同时对T和P都有直接影响,Le等人认为这种模型更符合间接范围限制的实际情况.

图3 CaseⅤ间接范围限制模型Fig.3 CaseⅤindirect range restriction model

CaseⅤ的关键是要估算出预测变量真分数T的范围限制比率uT,同时还需要估算出效标变量真分数P的范围限制比率uP,即

3.3.2 元分析矫正步骤

假如每个研究的预测变量和效标变量的受限与未受限信度已知,同时预测变量的受限和未受限方差已知,可以对每个研究的相关系数逐个矫正然后将它们加权汇总,步骤如下：

第一,矫正Y的受限信度rYYi对ρXYi的影响得到校正系数ρXPi(参考公式(3)).

第二,矫正rXXi对ρXPi的影响得到较正系数ρTPi(参考公式(14)).

第三,计算T和P的范围受限比率uT和uP(参考公式(21)和(22)).

第四,将指标带入以下公式得到单个研究未受限相关系数ρTPa,即

第七,计算总的效应量ρ(参考公式(7)).

如果个体研究未受限群体的信度和方差信息不全,与CaseⅡ和CaseⅣ一样研究者可以利用假设分布作为相关指标的计算依据,步骤如下：

第一,计算受限相关系数的平均值ρXYi(参考公式(8)).

第二,根据假设分布获取X的信度均值rXX、Y的信度均值rYY、X的范围受限比率均值uX、Y的范围受限比率均值uY.

第三,利用rXX、rYY、uX和uY计算出T和P的范围受限比率uT和uP,即

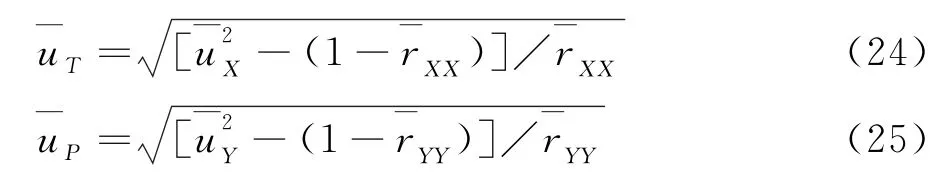
第四,将指标带入以下公式便可得总相关系数ρTP,即

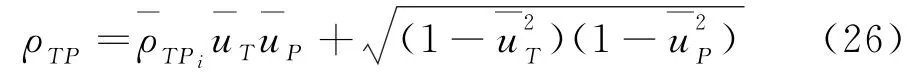
3.3.3 对CaseⅤ的评价

CaseⅤ和CaseⅣ一样不需要获取S的相关信息,所以它比CaseⅢ要更具实践意义.CaseⅤ不需要线性假设和方差同质性假设,与CaseⅡ比较起来这是优势.CaseⅤ另外一个优势是其矫正的相关系数允许符号的改变,因为S产生的间接范围限制不一定降低也有可能是增强X和Y的相关系数.[23]当然,获取Y的未受限群体的方差信息对于CaseⅤ来说也是有困难的.[10]另外,当X和Y的相关接近0时,S与X和Y的关系是随机的,这时候不好决定采用公式(19)还是公式(20),这是CaseⅤ的不足.[10]

4 总结

针对不同的范围限制选用不同的方法可以减少方法误用带来的误差.CaseⅠ和CaseⅡ矫正的是直接范围限制,CaseⅢ、CaseⅣ和CaseⅤ矫正的是间接范围限制,在使用条件满足的情况下,他们的矫正结果都是准确的.在实践中大多是间接而非直接范围限制,所以使用CaseⅡ时要谨慎.因为第三方变量信息的获取非常困难,所以CaseⅢ的使用就受到了极大的限制.而CaseⅣ虽然巧妙地避开了搜集第三方变量信息的难题,但是其核心假设(即假设S对P的影响全部由T中介)在现实研究中却不多见,所以比较起来CaseⅤ似乎更好,它既不用考虑第三方变量的信息,同时也不需要假设T完全中介S对P的作用.不过当预测变量和效标变量的相关系数接近0的时候,因为难以判断采用CaseⅤ的哪个矫正公式,这时使用CaseⅣ会更好.总之,方法的取舍需要研究者综合判断.