正弦波沟槽对湍流边界层相干结构影响的TR-PIV实验研究*

李山 姜楠† 杨绍琼2)‡

1) (天津大学机械工程学院, 天津 300072)

2) (青岛海洋科学与技术试点国家实验室, 青岛 266237)

1 引 言

流体阻力分为几种形式, 其中最为基本的是压差阻力和壁面摩擦阻力. 壁面阻力是由于流体与固体壁面相互作用及流体间的分子吸引力产生的.50多年来的实验和模拟的结果表明, 在近壁面湍流边界层中存在一系列的自维持运动[1−3]. 而在识别出的湍流运动中, 存在两个非常重要的事件, 即喷射事件和扫掠事件, 因为80%的湍动能都由这两个事件产生[4]. 扫掠事件一般发生在近壁=15以下, 与壁面剪切应力的产生紧密相连[5,6],对于减阻研究尤为重要, 因此, 对固壁表面进行调制改造以实现减阻更为容易且有效.

自然界中已自行演化出多种流动减阻的方法,其中具有代表性的为存在于鲨鱼表皮的微型鳞片结构, 大小一般在0.2–0.5之间, 凹槽的间距为30–100, 人们称之为“肤齿”, 沿着流动的方向排列, 形状类似于小沟槽, 有了这些沟槽似的微结构鲨鱼才能够保持清洁并快速游动[7−9]. 关于顺流向沟槽的研究始于20世纪80年代[10−13], 随后科研人员对其在层流边界层[12−14]、 转捩边界层[15]以及湍流边界层[5,16−18]中的减阻效果及其减阻机理进行了大量的实验和数值模拟研究. 已有研究结果发现, 当无量纲的沟槽高度和间距在一定范围内时具有减阻效果, Bechert等[17]和Walsh[19]在锯齿形沟槽壁面湍流边界层获得了约10%的减阻率(15). 关于顺流向沟槽的减阻机理, 目前有两种理论： 一是沟槽抑制了近壁的展向脉动[20−22]; 二是沟槽壁面边界层流向涡结构相较于光滑壁面有所抬升, 降低了流向涡与固壁表面的接触面积[21,23−26]. 流向沟槽减阻较全面的研究进展还可参考综述性文献[9,27,28].

迄今, 沟槽由于加工较困难, 减阻率受限以及产生的经济效益不足以补偿生产、维护及清理的费用等原因, 并没有得到广泛应用. 目前的改进措施遵循两条路径： 一是提高生产工艺和材料性能,Stenzel等[29]发明了一种自动的涂料应用技术, 可以将微沟槽直接压印在烤漆涂层上, 减少了沟槽内衬的使用和后续清理的费用; 另外一条路径, 也是本文的工作重点, 就是寻求可以提高沟槽减阻率的方法.

将传统顺流向呈直线排列的沟槽与其他减阻方法结合起来, 在近壁面流动中施加一个振荡的展向速度分量, 是一个很有吸引力的想法. Wassen等[30]和Grüneberger等[31]通过主动控制的方式, 使叶片形状的沟槽在展向上以沟槽与平板连接处为中心沿展向反复摆动, 模拟壁振荡, 他们的数值模拟和实验结果表明, 两种减阻技术叠加可以获得更高的减阻率. 但这种方式非常耗能, 在工程应用中存在明显劣势. 更为重要的是, 由于沟槽尖端的展向位移有限, 产生不了足够高的振幅, 在一定的流动工况下减阻率增加有限.

Quadrio和Luchini[32]提出一种新的改进思路, 通过沟槽在展向上沿波形曲线偏转, 以被动的方式来诱导一个周期性的近壁运动, 也就是将沿展向均匀的传统2D沟槽扩展为沿展向变化的3D沟槽, 比如模仿鲨鱼表皮的沟槽[8], 脊形的沟槽[33]以及波浪形沟槽[34,35]. Peet等[35]在槽道湍流中应用大涡模拟技术研究了= 180工况下锯齿形截面沟槽面流场的摩擦阻力(= 0.87,= 21).对于传统直线型沟槽, 减阻率为5.4%. 在沿展向正弦偏转的沟槽壁面, 当波长和振幅分别为1080和34个壁面单位时, 减阻率增加到7.4%, 提高了2%. 随后, Peet和Sagaut[36]将研究扩展到了无限薄沟槽和矩形沟槽中, 对于传统的矩形沟槽,计算得到11.2%的减阻率, 而在= 1080,=34的正弦波型沟槽壁面流场中减阻率达到14.6%.

本文以湍流边界层相干结构为主要分析对象,利用高时间分辨率粒子图像测速(time−resolved particle image velocimetry, TR−PIV)实验测量技术, 对正弦波型沟槽壁面(S−沟槽)的减阻机理进行了实验研究, 内容分为以下几个部分： 1)介绍实验装置及实验用沟槽模型; 2)从基本各阶统计量的角度分析S−沟槽对一阶、二阶统计量的影响, 并对比其与传统顺流向直线型沟槽的优缺点; 3)从相干结构的角度, 利用涡检测准则、相关函数等方法对不同壁面的流场进行细致分析, 探讨不同类型沟槽对湍流边界层中发卡涡及展向条带的影响.

2 实验设备和技术

TR−PIV实验在天津大学流体力学实验室开口式循环水槽中进行. 水槽实验段长度为532,内壁截面积为 2538(宽 × 高), 流速在30以下连续可调. 实验段整体由不锈钢板构成, 在测量区域内加工了一个矩形的窗口, 嵌入玻璃, 以实现PIV的无干扰测量. 在自由来流速度20的情况下, 测得流场背景湍流度为0.7%. 平板水平放置于水槽中, 与水槽底部距离为220,平板前缘按8：1的比例进行修型, 以避免流动分离.在距前缘100处放置直径为6的绊线加速自由来流转捩, 确保在实验段为充分发展的湍流边界层. 实验时水温保持在20, 在该温度下水的密度= 997.78, 运动黏度= 0.97937 ×.

2.1 实验模型

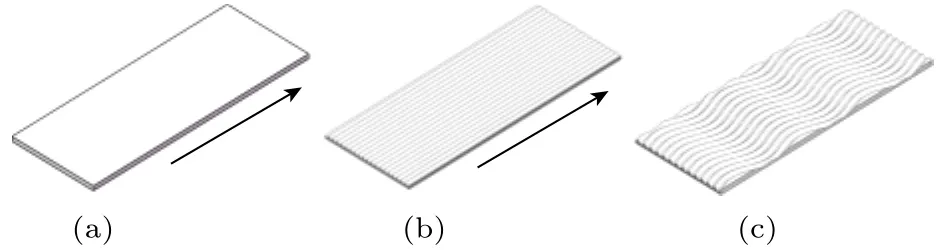
图1 实验模型示意图 (a) 光滑平板; (b) 传统直线型沟槽板; (c) 正弦波型沟槽板Fig. 1. Schematic diagram of experimental plates： (a)Smooth plate; (b) riblets; (c) s−riblets.

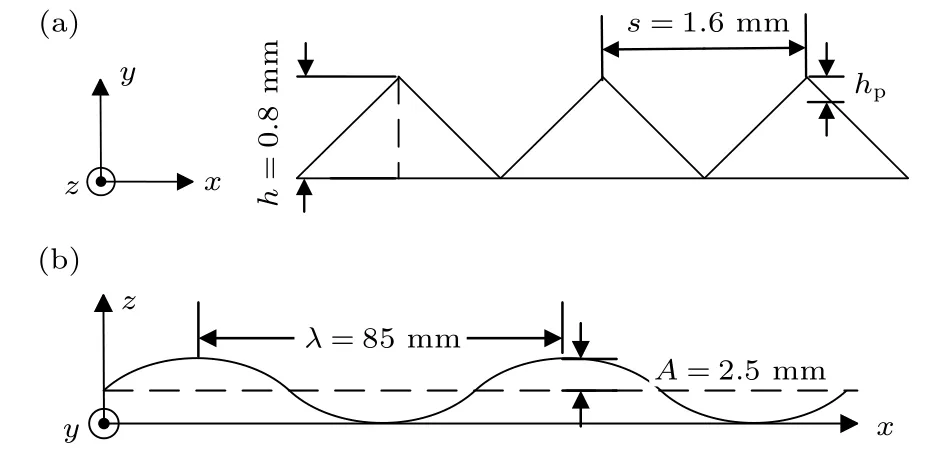
图2 正弦波沟槽截面图 (a) 左视图; (b) 俯视图Fig. 2. Cross section of s−riblets： (a) Left view; (b) top view.

2.2 实验测量技术

考虑到相干结构的三维特性, 实验分两部分进行, 分别测量充分发展湍流边界层中流−法向平面和流−展向平面. 在平面测量时, 激光片光源从水槽的下方垂直平板方向照亮平板中心区域, 与来流方向平行, 高速相机光轴与片光垂直, 布置图如图3(a)所示, 图中,,分别指流向、法向和展向. 在平面测量时,激光片光源以平行于实验平板的方向从水槽的侧方照亮流场, 法向高度可调节, 相机置于水槽底部,布置图如图3(b)所示. 在本次实验中共拍摄了三个平面, 分别距离实验平板1 , 5 和 9.实验中激光片光厚度约为1, 所使用示踪粒子为HGS−10型空心玻璃微珠, 粒径为10, 在流场中有良好的跟随性.

利用Dantec公司的TRPIV系统, 在来流速度分别为= 0.1,= 0.2的流速下, 对不同壁面的湍流边界层的流场进行了实验测量. 拍摄使用连续模式, 高速相机采样频率设定在500 Hz, 相机分辨率为1280像素1024像素, 粒子图像的物理范围为10582. 粒子在图像上的平均直径约为2个像素, 因此相关峰值锁定影响(peak−locking effect)可以忽略不计. 每个实验工况共记录6399张图像, 持续时间为12.8,为方便统计分析, 在每一个测量平面上进行了两次重复测量, 测量误差为1%左右[37−39].

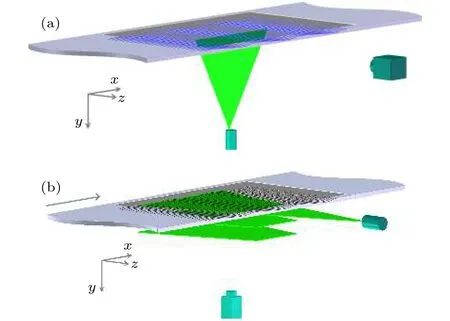
图3 实验装置示意图 (a) case 1; (b) case 2Fig. 3. Schematic diagram of experimental setup： (a) case 1;(b) case 2.

对测得的原始图像按照下列步骤进行处理：1)用背景消除法去除原始图像的背景噪声, 去除由于实验模型反光而产生的测量误差; 2)选取合适的查询窗口和重叠率对图像进行“自适应互相关”运算, 获得初始的速度矢量场; 3)对矢量场进行“上下限过滤”和“平均过滤”处理来消除速度场的噪声, 最终得到瞬时速度场. 进行自适应互相关计算时, 根据图像中粒子的位移, 对平面所选查询窗口尺寸为32 像素32 像素, 重叠率为75%, 最终所得到的每张瞬时速度场中包含148116(流向法向) 个矢量,及方向每两个相邻的速度矢量间物理分辨率约为0.71. 对平面粒子图像所选查询窗口尺寸和重叠率分别为64 像素64 像素和75%, 得到的矢量数为7761(流向展向),及方向的物理分辨率约为1.55.

3 统计量分析

3.1 平均速度

对于沟槽壁面的结果分析, 一个未解决的问题就是其速度剖面曲线原点位置的确定. 该问题首先由 Hooshmand等[40]提出, Bechert和Bartenwerfer[41]认为可以用黏性流体理论来解决.该原点位置位于沟槽尖端和谷底之间, 其与沟槽尖端的距离称为“凸出高度”, 决定了沟槽尖端深入到边界层内的距离. 根据已有研究结果以及本次实验中沟槽的形状和尺寸, 虚拟原点的位置定义为沟槽尖端点以下= 0.14处,为沟槽间距, 在两个雷诺数下分别相当于1.08和2.15个黏性长度(均用光滑壁面的摩擦速度进行无量纲化[41]. S−沟槽参数与直线形沟槽一致, 因此虚拟原点位置相同, 这一特征在无量纲速度剖面中有具体体现.

从表1中可以看出, 两个雷诺数下沟槽壁面都具有减阻效果, 边界层厚度增加, 其中=661.4时减阻率较高, 此时对应的无量纲沟槽间距为= 15.4, 处于较佳的减阻工况[17]. 正弦波沟槽的减阻率小幅增加, 在两个雷诺数下分别提高了0.58%和1.1%. 图4给出了相同雷诺数下三种不同壁面的流向平均速度的分布曲线, 均用进行无量纲化, 同时给出了经典的黏性底层和对数律曲线做对比. 根据樊星和姜楠[42]提出的利用平均速度剖面测量的方法, 基于平板湍流边界层对数区无量纲速度和法向高度满足的对数关系, 利用牛顿迭代法和最速下降法拟合获得壁面摩擦速度. 从图4中可以看出,两个流速下光滑壁面的速度剖面与湍流边界层的经典分布较符合, 沟槽壁面上流场的平均速度在缓冲层明显提高, 对数区上移, 在= 337.8时, 沟槽壁面的常数B值分别为= 5.9,= 6.3;在=661.4时, 分别为=6.05,=6.42,符合减阻壁面流场的典型特征[26,43,44].

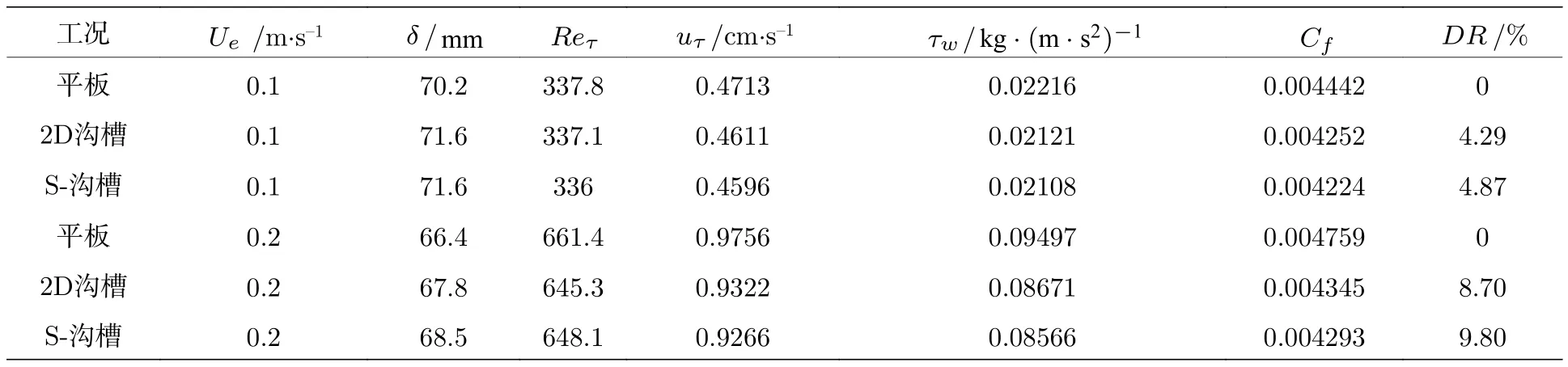
表1 湍流边界层基本参数及减阻率Table 1. Basic parameters and results for turbulent boundary layers over test plates.

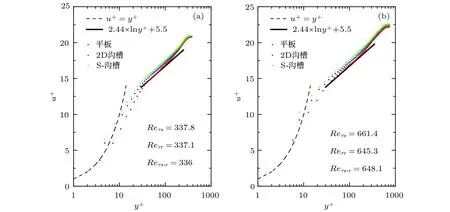
图4 不同壁面流场的流向平均速度剖面Fig. 4. Mean velocity profiles in TBL flows over test plates.

3.2 湍流度和雷诺切应力

雷诺切应力是由于湍流脉动速度引起动量交换而产生的附加应力. 图6比较了光滑壁面和沟槽壁面流场的雷诺切应力–沿法向位置的分布,其中–进行无量纲化. 图 6(a)中=337.8, 光滑壁面流场雷诺切应力在30的位置出现明显峰值, 两种沟槽壁面流场的雷诺切应力的峰值均大幅度降低, 且有外移现象. 图6(b)中=661.4, 现象相同. 雷诺切应力的降低是减阻壁面的典型特征, 说明湍流中的动量交换减弱, 湍流脉动被有效抑制.

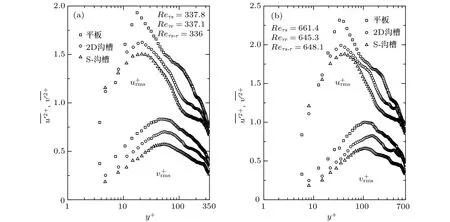
图5 不同壁面流场湍流度的分布曲线Fig. 5. Distribution of turbulent intensities over test plates.

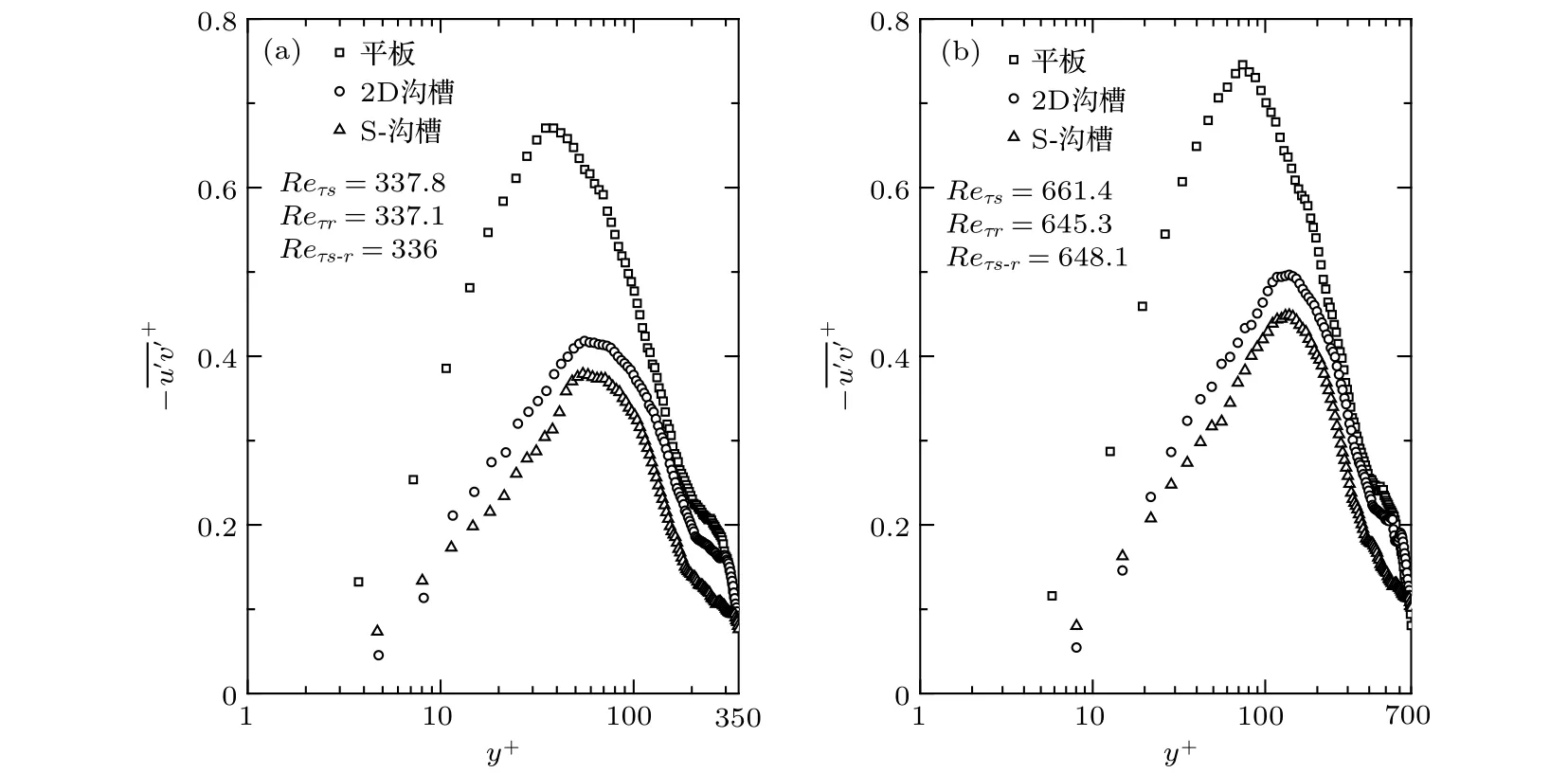
图6 不同壁面流场雷诺切应力的分布曲线Fig. 6. Distribution of Reynolds shear stress over test plates.

4 相干结构分析

4.1 基于流-法向平面的相干结构分析

从上文可以看出, 两种沟槽都产生了减阻效果, 但从统计量分析并不足以分析减阻的机理, 因为三种壁面的分布趋势是相似的. 因此下文将从流场中相干结构的角度来做进一步的讨论. 相关函数作为经典的统计分析方法, 能提供湍流场中相干结构的空间尺度信息. Jiménez[45]对利用脉动速度的空间相关函数来提取相干结构做了综述性的介绍,并给出了边界层内不同速度分量的脉动速度的相关函数的分布特征. Chen等[46]提出一种新的提取方法, 利用速度与涡量的相关函数来辨识槽道湍流中的相干结构, 给出了壁湍流中准流向涡和条带结构的统计结果和尺度信息, 该方法物理意义明确.Farano等[47]在不同的雷诺数的湍流边界层流场中也得到了很好的结果. 本文利用经典的流向脉动速度的二维空间相关函数, 来研究光滑壁面和沟槽壁面湍流边界层中相干结构的空间尺度和空间形态, 关于脉动速度与涡量的相关函数的结果会在后续的工作中进行进一步的讨论. 湍流边界层流向脉动速度的二维空间相关系数定义为

相关函数分析辨别的是与参考点有相同动量通量的区域所呈现的拓扑结构, 是一种广义上的相干结构提取方法.准则排除了流场中剪切较强但无涡旋存在的区域, 相对来说更能准确地反映出涡结构的运动特征. 流场中的涡结构承担了流场中能量和动量的传递及交换, 是摩擦阻力大幅增加的关键原因. 本文应用准则对光滑和沟槽壁面上平面内的涡结构进行了条件平均的辨识和提取, 对比了不同壁面上的发卡涡的拓扑形态.准则是由Zhou等[50]最早提出的, 他认为当速度梯度的张量的特征值有一个实数和一对共轭复根时, 当地的流场就存在局部的旋转运动, 速度梯度张量可以分解为

图8 特征向量空间中的局部流动[50]Fig. 8. The local motion in the space spanned by the eigen−vectors[50].

湍流边界层喷射事件和扫掠事件是近壁区雷诺切应力的主要贡献者, 是湍流能量和动量输运的“媒介”. 对比图9中不同壁面的结果, 当=71.1时, 在光滑壁面上剪切层的倾角为, 沟槽壁面的为, S−沟槽的已经降到, 说明沟槽壁面的存在使得流场结构在向下游迁移过程中, 向上抬升的趋势受到了抑制, 即沟槽壁面限制了发卡涡在法向上的运动; 在= 128时现象相同, 正弦波沟槽对其抑制更为明显. 发卡涡诱导的猝发事件在湍流的自维持和发卡涡包的自生成过程中也是不可缺少的一环, 其强度的降低说明沟槽也削弱了湍流的自维持机制[52].

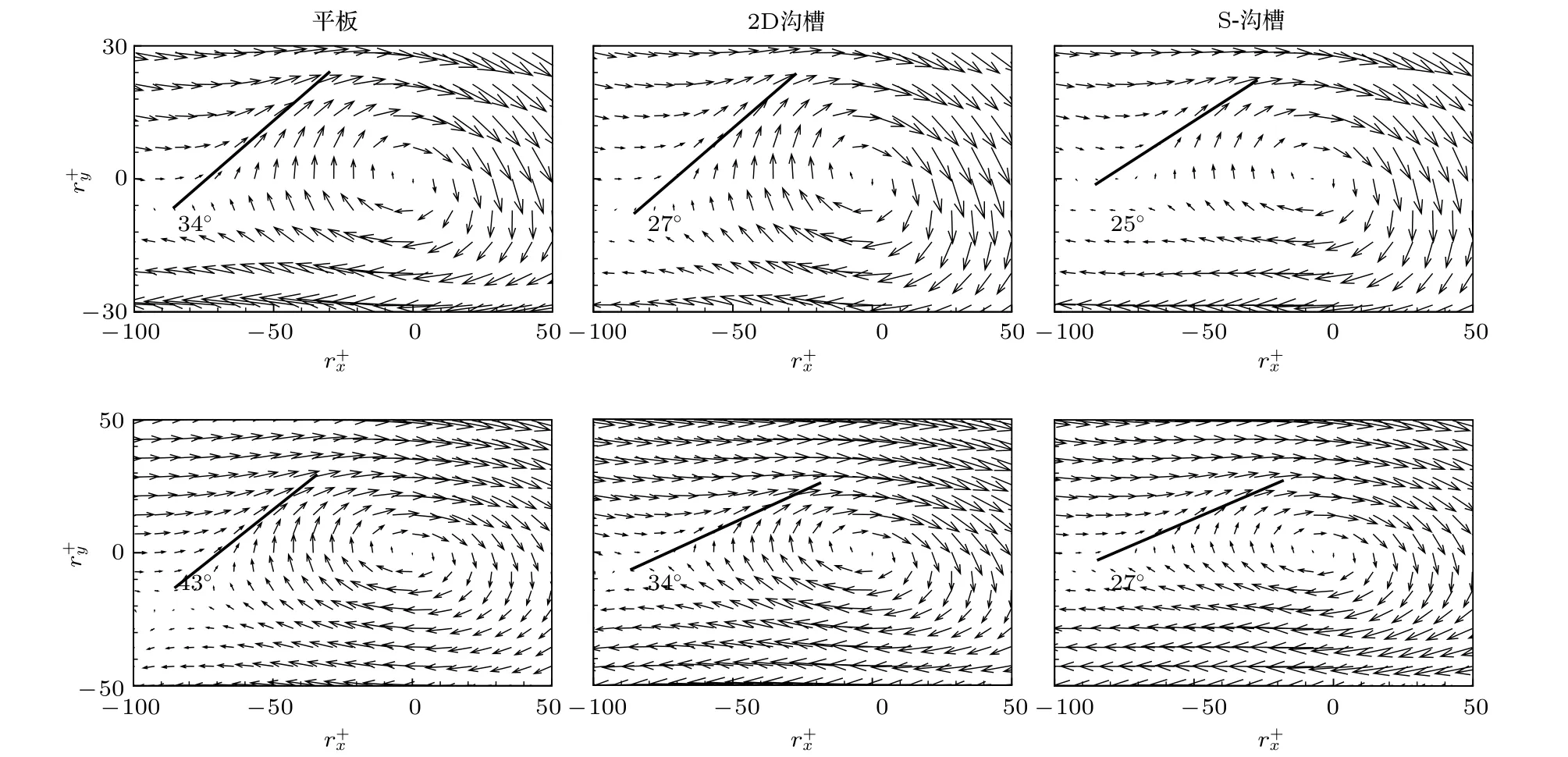
图9 平面条件平均相干结构 (上) = 71.1; (下) = 128Fig. 9. Conditionally−averaged structure in the plane： (top) = 71.1; (bottom) = 128.

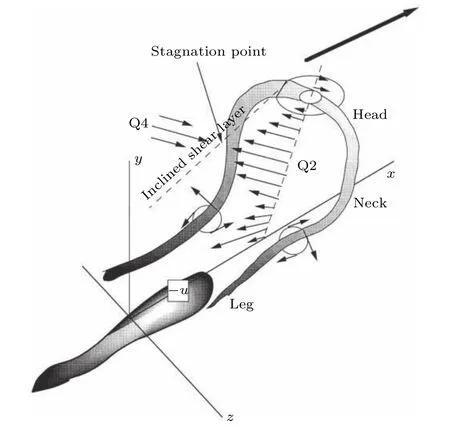
图10 Adrian等[51]提出的发卡涡模型Fig. 10. The model of hairpin vortex proposed by Adrian et al.[51].

4.2 基于流-展向平面的相干结构分析

由于相干结构演化和发展的三维特性, 单一的平面测量无法完整地研究不同沟槽对其的影响, 因此对流−展向平面结构特征的研究很有必要, 下文给出= 661.4减阻率较高时, 在不同法向高度不同沟槽对展向流动结构的影响.

Kline等[53]最早用实验证明了在近壁区2.7位置的流−展向平面上, 相干结构主要为沿展向分布的高低速条带, 条带结构沿展向的平均无量纲间距为= 100, 沿流向的平均长度约为1000个黏性长度. 随后 Nakagawa和 Nezu[54]以及Smith和Metzler[55]的研究结果进一步证明,在10的范围内基本恒定在100左右, 而且在雷诺数6000时,的大小不随雷诺数改变; 而在10时,随法向位置的增加而略有增大.

为了对近壁条带结构进行量化分析, 本文用流向脉动速度在空间上的自相关函数沿展向的分布来表征条带的间距大小, 表达式为

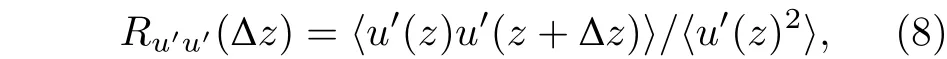
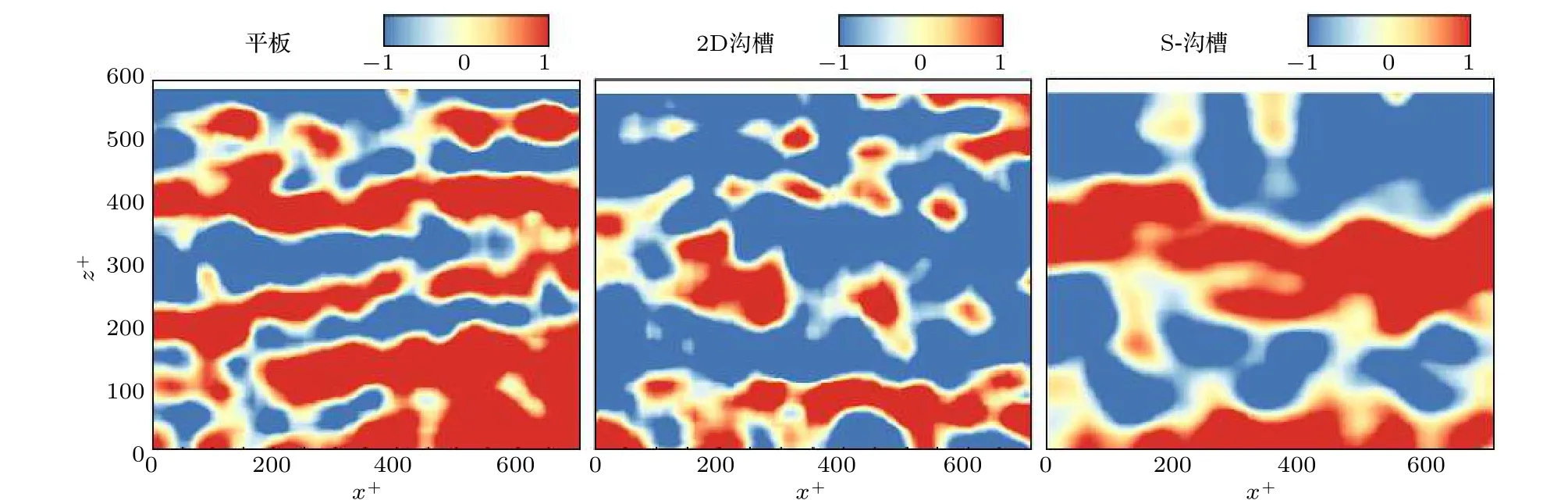
图11 平面内不同壁面上流场 = 9.7流向脉动速度云图Fig. 11. Instantaneous streamwise fluctuating velocity in plane at = 9.7.

图12 不同壁面上流场 沿展向的自相关函数Fig. 12. Autocorrelation function of in the −direction over test plates.

5 结 论

本文利用 TR−PIV 测速系统, 分别从流 − 法向、流 − 展向两个不同的平面角度测量二维顺流向和三维正弦波沟槽湍流边界层, 利用相关函数、涡检测准则辨识提取不同壁面湍流边界层中相干结构, 分析了不同壁面条件对其产生的影响, 得到以下结论.

(1) 不同雷诺数工况下对各阶统计量进行了对比, 结果表明, 两种沟槽壁面的平均速度剖面满足减阻壁面的典型特征, 在对数区都有不同程度的抬升, S−沟槽的减阻率更大. S−沟槽近壁区平均速度增大, 壁面摩擦阻力减小. S−沟槽湍流度和雷诺切应力也有明显的降低, 流向湍流度和雷诺切应力的峰值远离壁面外移, 降低了近壁区的动量和动能的输运.

(2) 基于相关函数方法, 从统计平均的意义上来研究近壁区的结构, 提取了不同壁面湍流边界层中的相干结构. 结果表明S−沟槽也减小了流向相干运动在流向和法向上的空间尺度, 且相干结构与主流之间的倾角明显减小, 抑制了流体在法向上的运动及流场结构的抬升.

(3) 对比不同壁面上湍流边界层发卡涡的倾斜角度及其诱导的喷射和扫掠猝发事件, 发现沟槽抑制了喷射和扫掠运动事件的强度, 降低了雷诺切应力, S−沟槽作用效果更为明显. 两种沟槽壁面湍流边界层中发卡涡头的倾斜程度都有明显降低, S−沟槽效果也更为突出, 即沟槽结构能够抑制近壁区的湍流自维持过程, 抑制发卡涡的形成, 与发卡涡对应的喷射和扫掠能力也相对降低, 进而减少了近壁区与湍流核心区动量和能量的交换, 从而达到减阻的效果.

(4) 在同一雷诺数下, 随着法向位置的增加,三种壁面的条带间距都有所变宽. 在同一法向位置处, 两种沟槽壁面的条带间距都大于光滑壁面, 说明近壁区沟槽壁面的流场结构更为规则有序, 条带在展向上的运动受到了抑制, 影响了高低速条带之间的相互作用.

最后需要指出的是, 在本文的雷诺数流场工况下, 三维正弦波沟槽与二维直线型沟槽相比, 减阻机理相同, 但效果更好. 后续, 其波长和振幅的参数优化设计研究尤为关键.