相依网络的条件依赖群逾渗*

韩伟涛 伊鹏

(国家数字交换系统工程技术研究中心, 郑州 450000)

1 引 言

现实世界中的许多复杂系统都可以用复杂网络描述, 例如生物神经系统、社交网络、交通系统、互联网等[1−3]. 随着研究人员对复杂网络认识的逐渐深入, 相关研究成果已成为人们理解现实世界复杂系统的重要工具. 但现实生活中的复杂系统通常并不是孤立的, 往往多个系统之间存在相互依赖关系, 这种依赖性会导致网络鲁棒性的急剧下降.2003年意大利大停电是典型的相依网络级联失效引起的重大生产事故, 最初电网和通信网中极少的节点失效使意大利接近半数的电力设施瘫痪, 数百万人失去电力供应[4]. 在单个网络中, 随着初始删除节点比例增大, 网络巨分量(giant component)连续减小, 整个解体过程呈现出二阶相变, 但在多个相依网络, 巨分量减小的过程多为一阶相变, 表明相依网络的鲁棒性远不如单个网络. 近些年来,相依网络的鲁棒性开始引起研究人员的重视[3,5−13],网络鲁棒性研究主要基于经典统计物理的逾渗模型[14], 该模型能准确描述网络解体的相变过程.

以往关于相依网络鲁棒性的研究主要针对一对一相依节点[12,15−19], 但在现实情况中, 一个节点往往会依赖于多个节点[6], 这多个被依赖节点称为该节点的依赖群. 例如一个通信基站会有多个电厂为其供电, 食物链中一种生物会捕食多种生物. 近年来, 已有学者对存在依赖群的网络展开了研究.Shao等[6]提出了一种耦合网络中存在依赖群的模型, 该模型认为只有当某节点依赖群的全部节点失效后该节点才会失效, 这种依赖模式有效改善了相变点. Wang等[20]研究了网络的群渗流现象, 网络节点的存活取决于其所在超级节点是否连向巨分量, 这种网络模型在一定程度上提高了网络的鲁棒性, 但逾渗类型仍然是一阶相变. Parshani等[7]研究了单个网络中存在依赖群的情况, 发现随着依赖群规模增大网络会变得更加脆弱, 极少数节点失效会导致整个网络崩溃. Wang等[9,21]提出了一种单个网络中存在条件依赖群的模型, 认为当某节点依赖的节点失效数量超过一定比例时该节点才失效,研究发现随着失效比例阈值增大, 一阶相变甚至会变为二阶相变.

本文研究了具有多依赖节点的相依网络的逾渗现象, 提出相依网络的条件依赖群逾渗模型并给出巨分量相变方程. 仿真结果表明, 在确定依赖度分布的情况下, 相依网络逾渗模拟结果与方程数值解相吻合, 并且通过增大失效容忍度或依赖群规模可增强网络鲁棒性. 虽然模型对于任意依赖度分布的相依网络不存在二阶相变, 但本文所述逾渗模型对提高相依网络鲁棒性仍具有一定指导作用.

本文的内容主要包括： 第2部分阐述相依网络的条件依赖群逾渗模型的基本概念; 第3部分通过理论分析给出模型的巨分量相变方程; 第4部分仿真验证理论框架有效性; 第5部分讨论本文研究成果; 第6部分是结论.

2 模 型

传统相依网络逾渗模型多为一对一依赖, 一对一依赖可使网络满足无反馈条件, 便于理论分析[3],但严格的一对一依赖在现实网络中通常是不存在的, 一个网络节点可能会依赖于另一个网络的多个节点, 若节点依赖的所有节点中有任意一个节点失效, 按照传统模型的分析方法, 该节点也会失效,如图1所示.

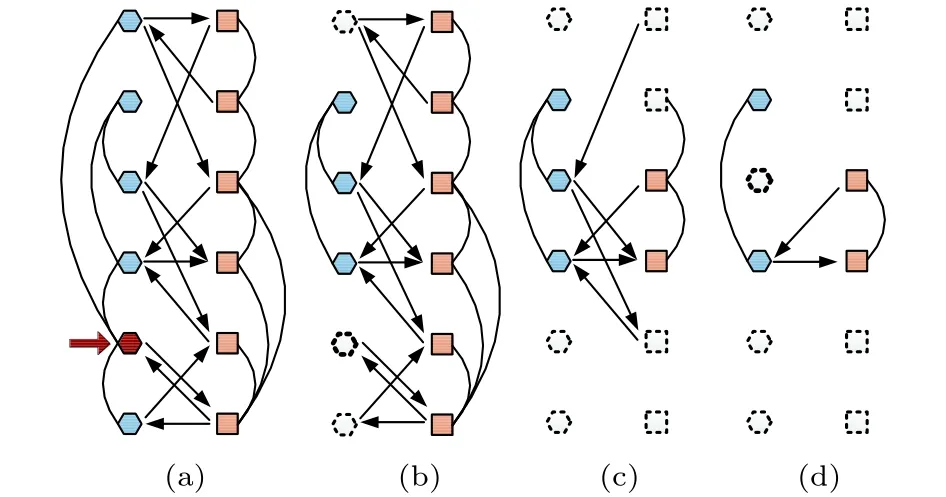
图1 具有多依赖关系的相依网络逾渗示意图, 初始攻击导致红色节点失效, 随后发生级联失效过程, 最终相依网络仅有极少数节点存活Fig. 1. The model of percolation of interdependent net−works with multiple support−dependence relations. The red node fails after the initial attack. Then the cascading fail−ure process leads to a catastrophiccollapse of the interde−pendent networks. Finally, only a small fraction of nodes survive.

这种严格的多依赖关系会大幅降低相依网络的鲁棒性, 少部分节点失效就会造成相依网络完全崩溃. 但现实中的网络却没有这么脆弱. 通过观察可以发现, 只要依赖群有部分节点存活则依赖节点仍有效, 例如在某产业链中, 存在生产同类型产品的工厂若干, 其中少部分同类工厂倒闭并不会导致有关产业链的瘫痪[9]. 因此本文提出了一种允许部分相依节点失效的相依网络逾渗模型, 用以描述在部分被依赖节点失效情况下依赖节点仍正常工作的现象, 如图2所示.

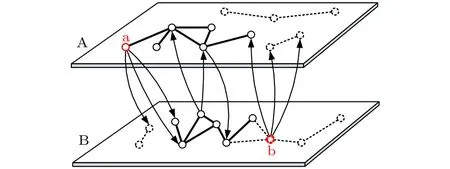
图2 相依网络的条件依赖群逾渗模型 A网络节点随机依赖于B网络的 个节点( ), 反之亦然; A网络的a节点依赖的3个节点有一个失效, 但失效比例未超过容忍度 , a节点继续工作; B网络的b节点依赖的节点失效比例超过 , 所以b节点失效Fig. 2. The model of percolation in interdependent net−works with conditional dependency clusters. Nodes in net−work A randomly depends on ( ) nodes in network B and vice versa. One of the three nodes which node a in network A depends on fails, but the failure proportion does not exceed , node a still works. Two of the three nodes which node b in network B depends on fail, the fail−ure proportion exceeds , node bfails.

3 理论分析

本文提出的相依网络逾渗模型级联失效过程如下.

Step 3： 循环进行Step 2, Step 3直至相依网络中不再有新的节点失效.

根据生成函数理论[22], 网络的度分布生成函, 余度分布生成函数为, 其 中表 示 任 取一个节点其度为的概率,表示网络的平均度.随机删除网络比例节点后, 令为随机选择一条边连接的节点通向巨分量的概率, 则满足自恰方程

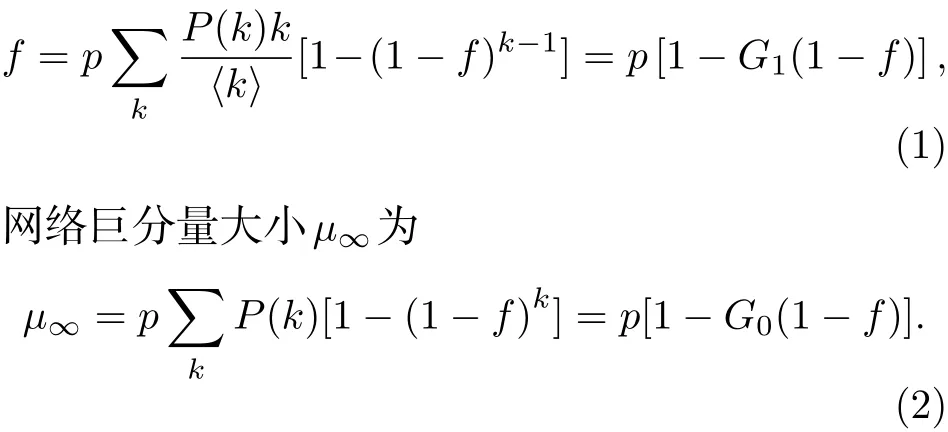
对于单个网络, 联立上述两式可解出巨分量的大小. 传统的一对一相依网络求解与单网络相似,这里直接给出[23]

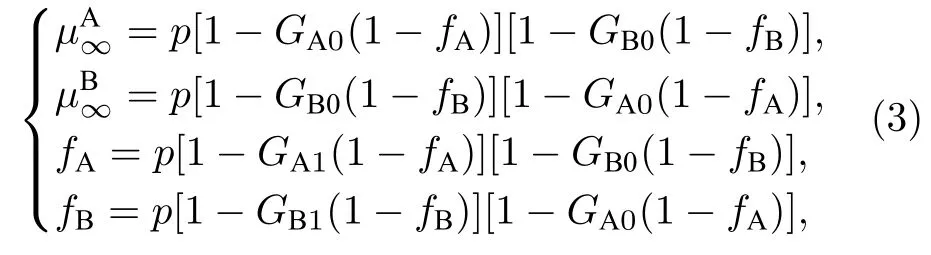
与一对一相依网络情况不同, 本文提出的模型一个节点可依赖多个节点, 只有当某节点依赖的节点失效比例超过容忍度时, 该节点失效, 令表示在 i 网络中随机选择节点的依赖群失效比例不超过的概率, 则本文模型关于巨分量的方程为

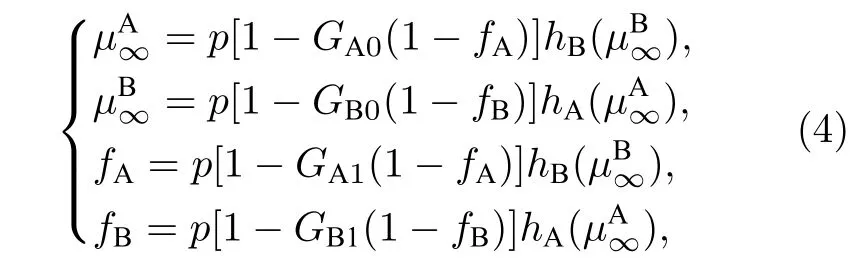
其中

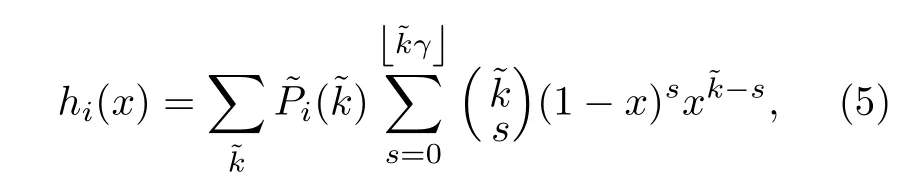
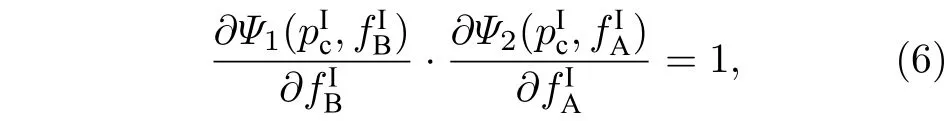
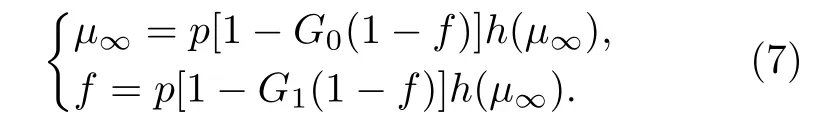
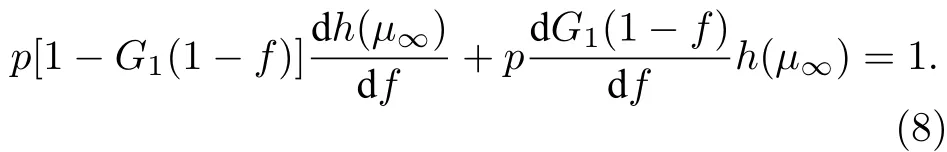
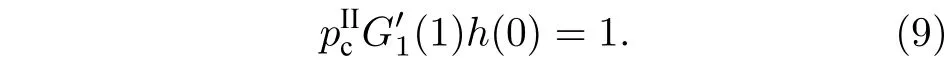
4 仿 真

4.1 RR-RR相依网络

随机规则(random regular, RR)网络的度分布生成函数为, 余度分布生成函数为. 假设两个RR网络具有相同的分布, 那么将两个生成函数代入(7)式可得方程

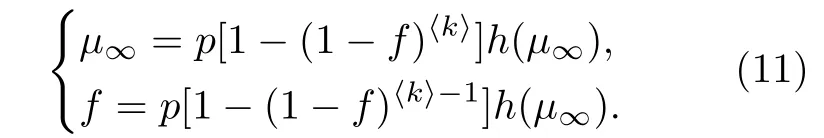
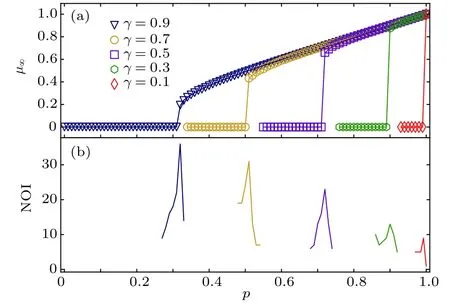
图3 不同 取值的RR−RR相依网络逾渗, 每个网络节点数 , 平均度 , , 空心标记为仿真值, 实线为逾渗方程数值解 (a) 巨分量 与 对应关系; (b) 级联失效迭代次数(number of iterations, NOI)Fig. 3. The results of the percolation of RR−RR interde−pendent networks for different , each network has 200000 nodes, average degree is 6, . The symbols repres−ent the simulation results, and the solid linesshow the cor−responding analytical predictions. (a) The size ofthe giant component versus ; (b) number of iterations.

4.2 ER-ER相依网络

Erdös−Rényi (ER)网络[24]的度分布与余度分布生成函数相同, 都为,假设两个ER网络具有相同的分布, 那么将两个生成函数代入(7)式可得方程

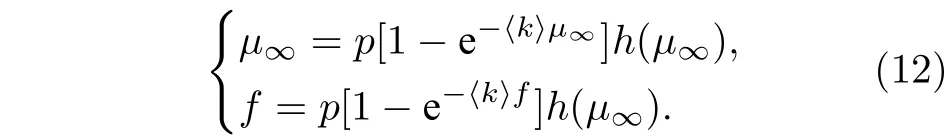
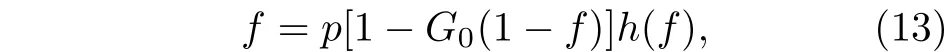
上式即为相同度分布的ER−ER相依网络巨分量方程. 定义如下：

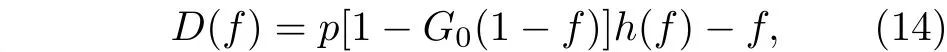
4.3 SF-SF相依网络

无标度网络(scale free network, SF)是指服从于分布的随机网络, 它的度分布生成函数和余度分布生成函数可以分别近似为[12]：

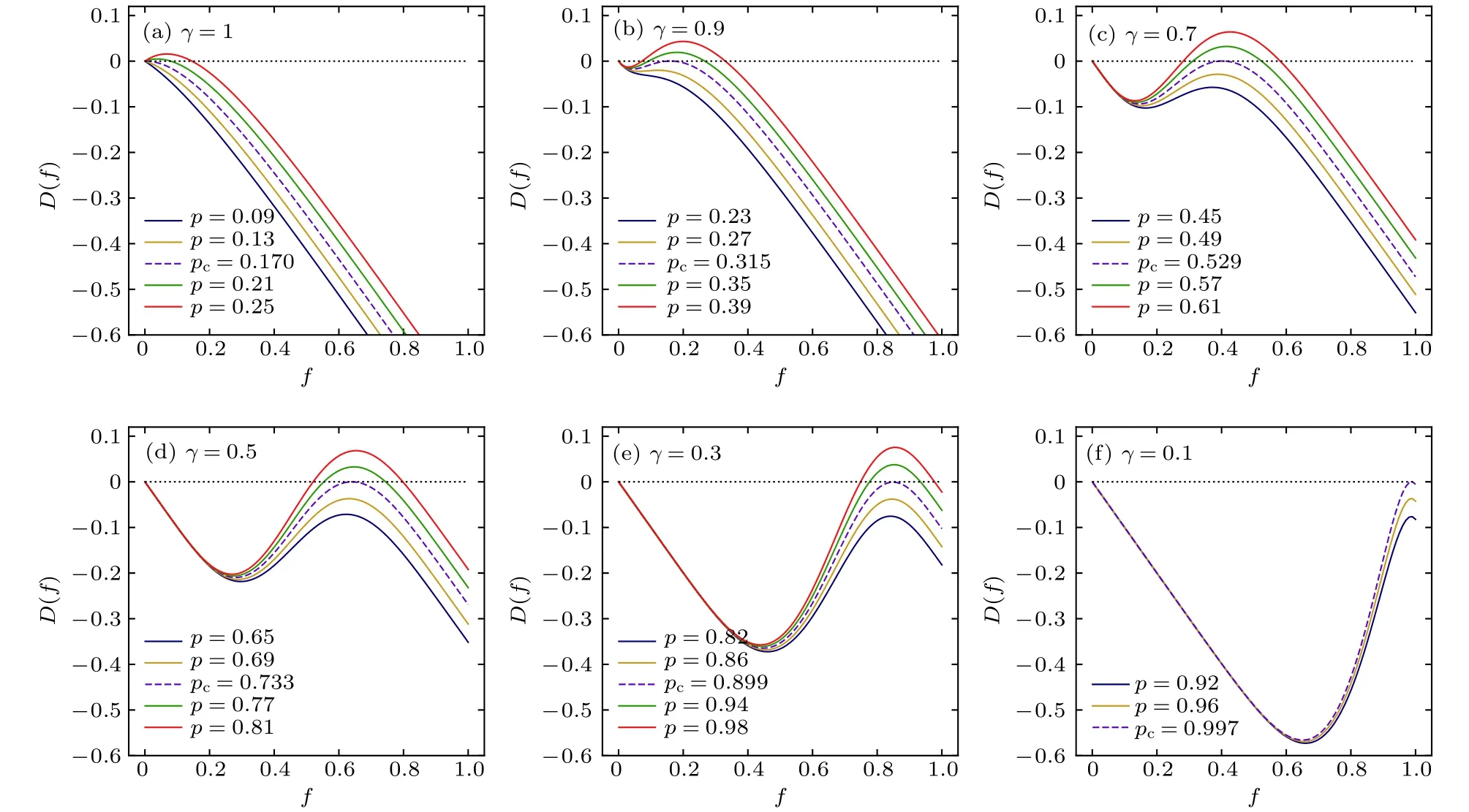
图4 不同 值对应的ER−ER相依网络相变点, 网络平均度 ,Fig. 4. Graphical solutions of ER−ER interdependent networks transition for different . The average degree is 6, .

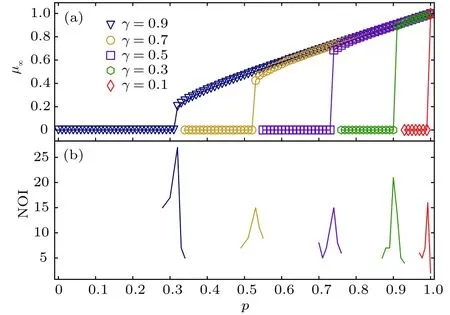
图5 不同 取值的ER−ER相依网络逾渗, 每个网络节点数 , 平均度 , , 空心标记为仿真值, 实线为逾渗方程数值解 (a) 巨分量 与 对应关系; (b) 级联失效迭代次数Fig. 5. The results of the percolation of ER−ER interde−pendent networks for different , each network has 200000 nodes, average degree is 6, . The symbols repres−ent the simulation results, and the solid linesshow the cor−responding analytical predictions. (a) The size ofthe giant component versus ; (b) number of iterations.

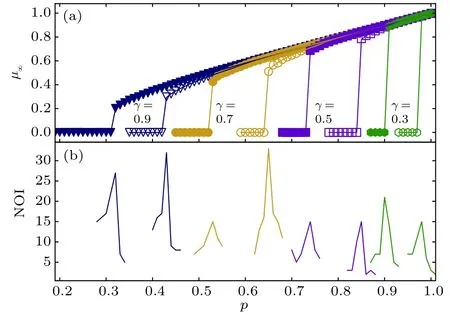
图6 不同依赖度分布的ER−ER相依网络逾渗,, 分别用实心和空心标记表示, 每个网络节点数 , 平均度 (a) 巨分量 与对应关系; (b) 级联失效迭代次数Fig. 6. The results of the percolation of ER−ER interde−pendent networks for different dependency degrees, each network has 200000 nodes, average degree is 6. The depend−ency degrees are (solid symbols) and(empty symbols). (a) The size ofthe giant componentversus ; (b) number of iterations.

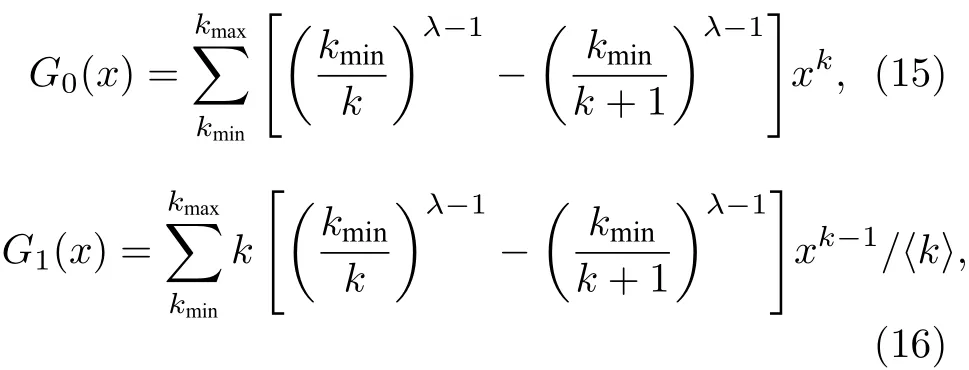
图7 不同 取值的ER−ER相依网络相变点, 空心标记为仿真结果, 实线是理论值Fig. 7. The critical point versus of ER−ER interde−pendent networks, The symbols represent the simulation results, and the solid linesshow the corresponding analytic−al predictions.

将两个生成函数代入(7)式可求出巨分量. 图8给出了不同取值的SF−SF相依网络逾渗仿真结果.

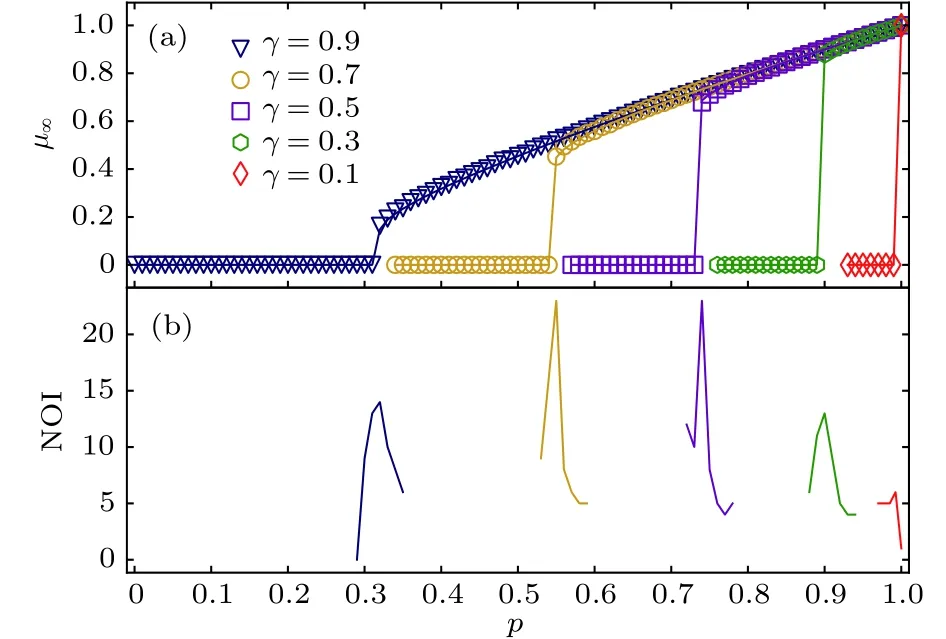
图8 不同 取值的SF−SF相依网络逾渗, 每个网络节点数 , 平均度 , , , 空心标记为仿真值, 实线为逾渗方程数值解 (a) 巨分量与 对应关系; (b) 级联失效迭代次数Fig. 8. The results of the percolation of SF−SF interdepend−ent networks for different , each network has 200000 nodes, average degree is 6, , . The sym−bols represent the simulation results, and the solid li−nesshow the corresponding analytical predictions. (a) The size ofthe giant component versus ; (b) number of it−erations.

5 讨 论

2) 通过观察图3, 图5以及图8的仿真结果可以看出, 在本文选取的值范围内, 三种相依网络皆不存在二阶相变, 这与理论分析的结果吻合.

根据本文理论分析与仿真结果可知, 可从两个方面提高多依赖相依网络鲁棒性：

2) 增加依赖节点的数量, 若某节点存在更多的依赖节点, 则在相同值的情况下存活节点组合更多, 从而提高该节点存活的概率.

6 结 论

相依网络的鲁棒性正在逐渐引起人们的重视,现实网络中节点往往会依赖于多个节点, 按照传统相依网络逾渗理论, 多依赖性通常会降低网络鲁棒性, 但现实网络并未因此变得更脆弱. 为了更好地描述现实网络中的这种现象, 提出了一种相依网络的条件依赖群逾渗模型, 该模型允许在部分被依赖节点失效情况下依赖节点仍正常工作. 本文在逾渗模型的基础上, 利用生成函数理论[25]给出了上述具有任意度分布模型的巨分量方程, 通过对三种相依网络模拟仿真可看出方程的数值解与模拟值相吻合, 验证了理论的有效性. 虽然理论分析发现对于任意依赖度分布的相依网络模型, 无论取任何值(除外)都不存在二阶逾渗相变, 但仿真结果仍表明随着取值增大网络鲁棒性会逐渐提高.此外, 对比不同依赖度分布的仿真, 在相同值的情况下, 随着依赖节点的增多, 网络鲁棒性也会相应地提升. 本文的研究结果对提高现实世界相依系统鲁棒性具有一定的科学指导意义, 同时也为后续具有多依赖关系的相依网络研究提供了借鉴.